Презентация "Задачи символьной алгебры в пакетах символьной математики" (11 класс) по информатике – проект, доклад
Презентацию на тему "Задачи символьной алгебры в пакетах символьной математики" (11 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 34 слайд(ов).
Слайды презентации
Список похожих презентаций
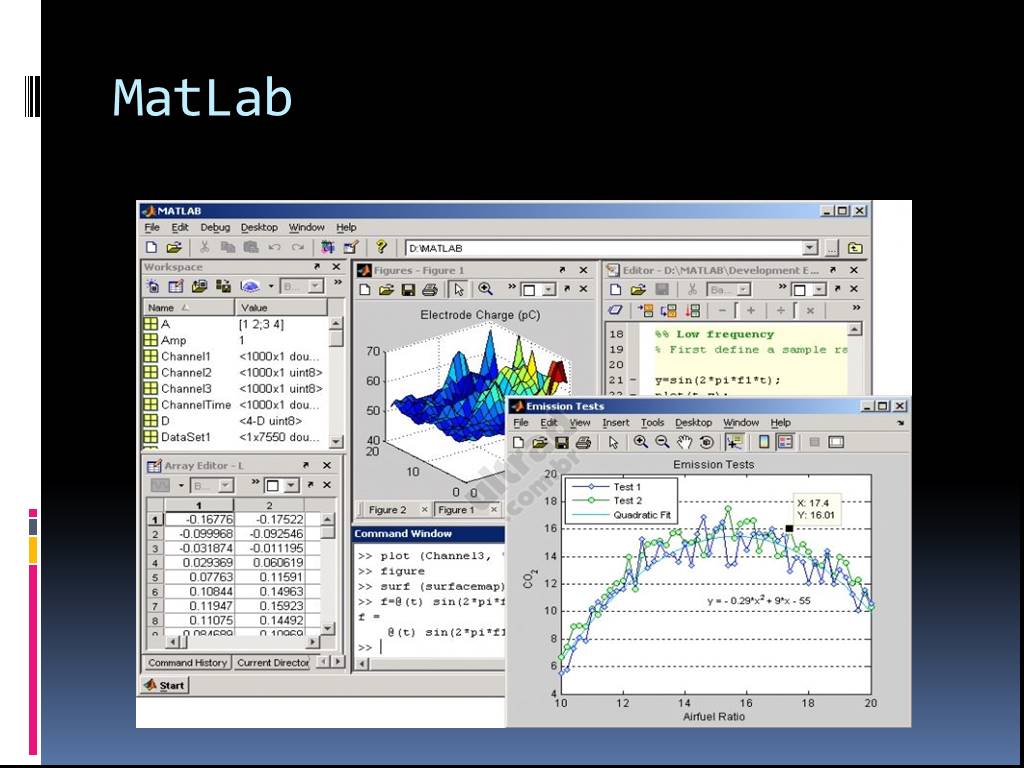
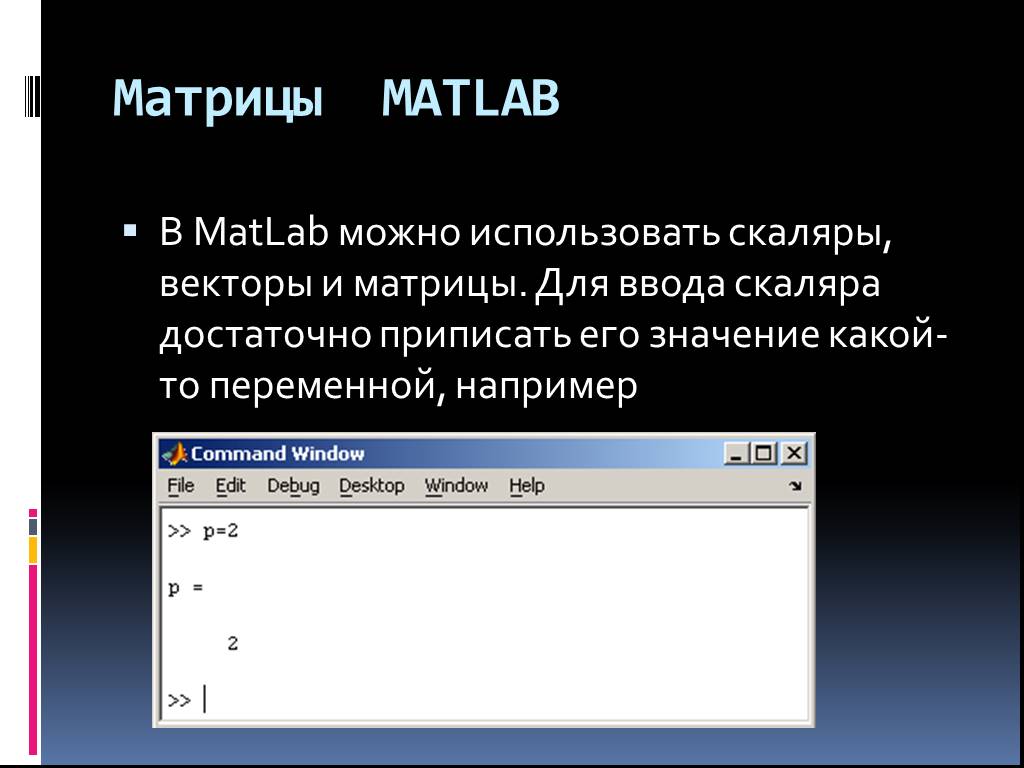
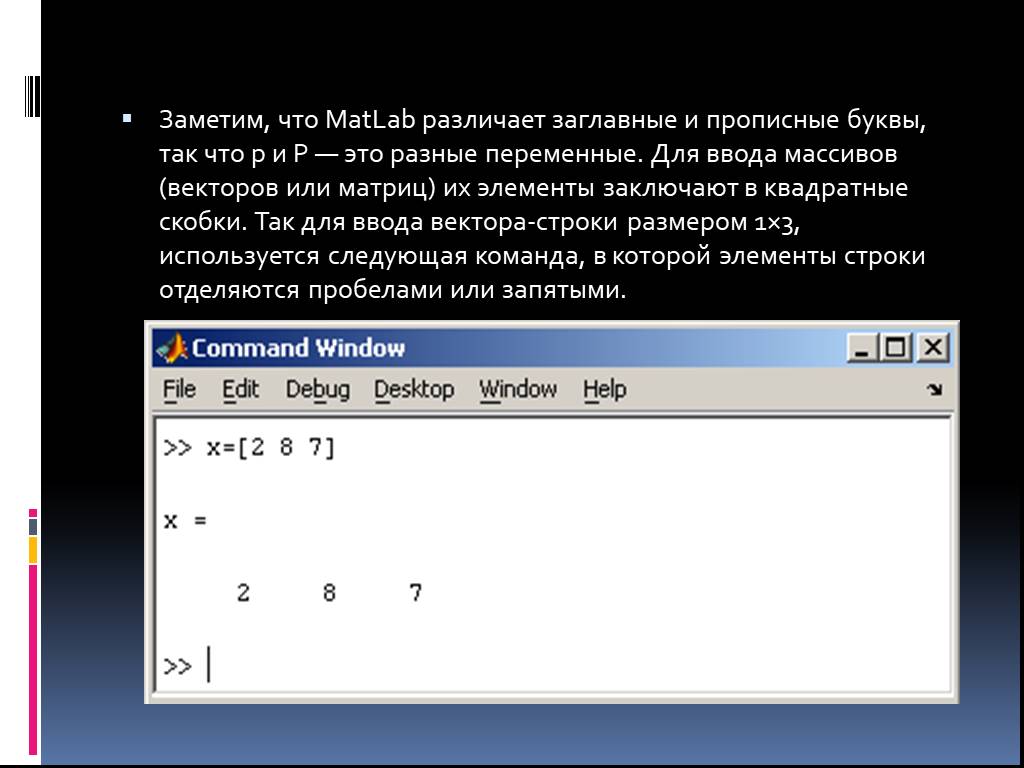
Интерактивная работа в системах символьной математики
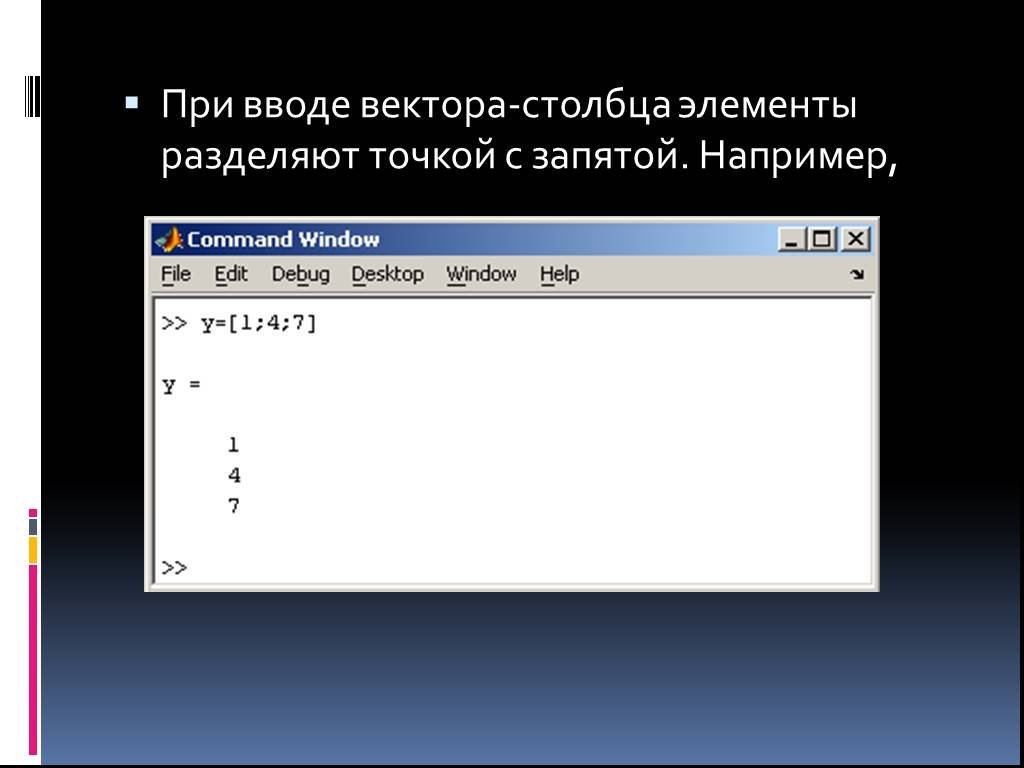
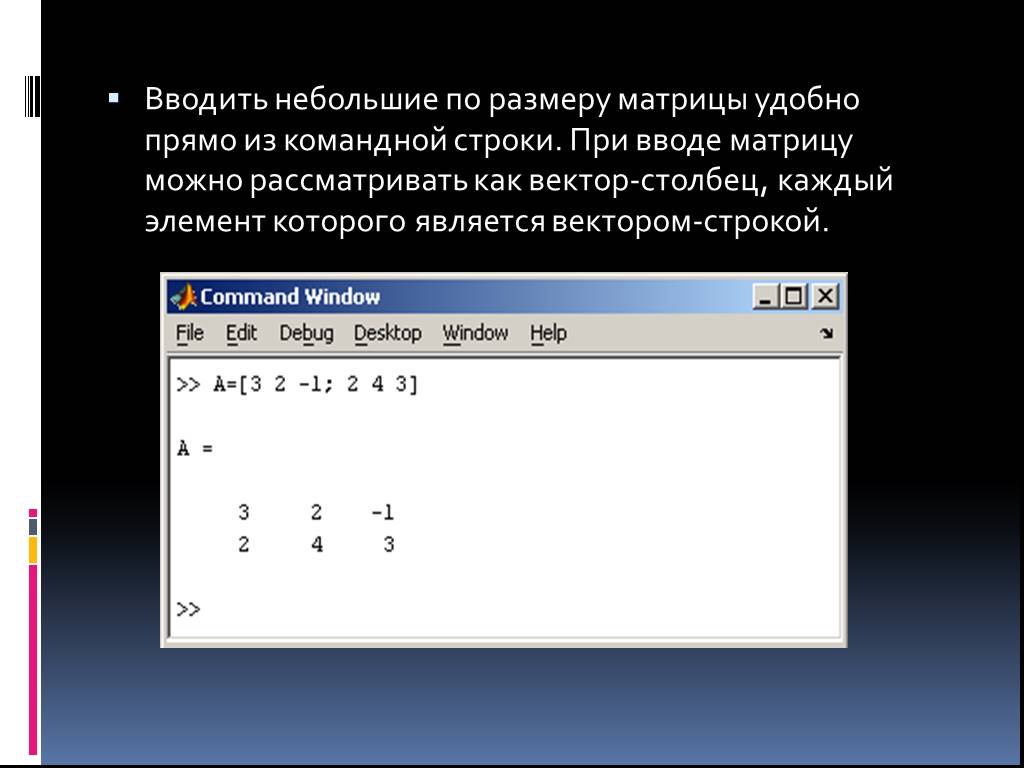
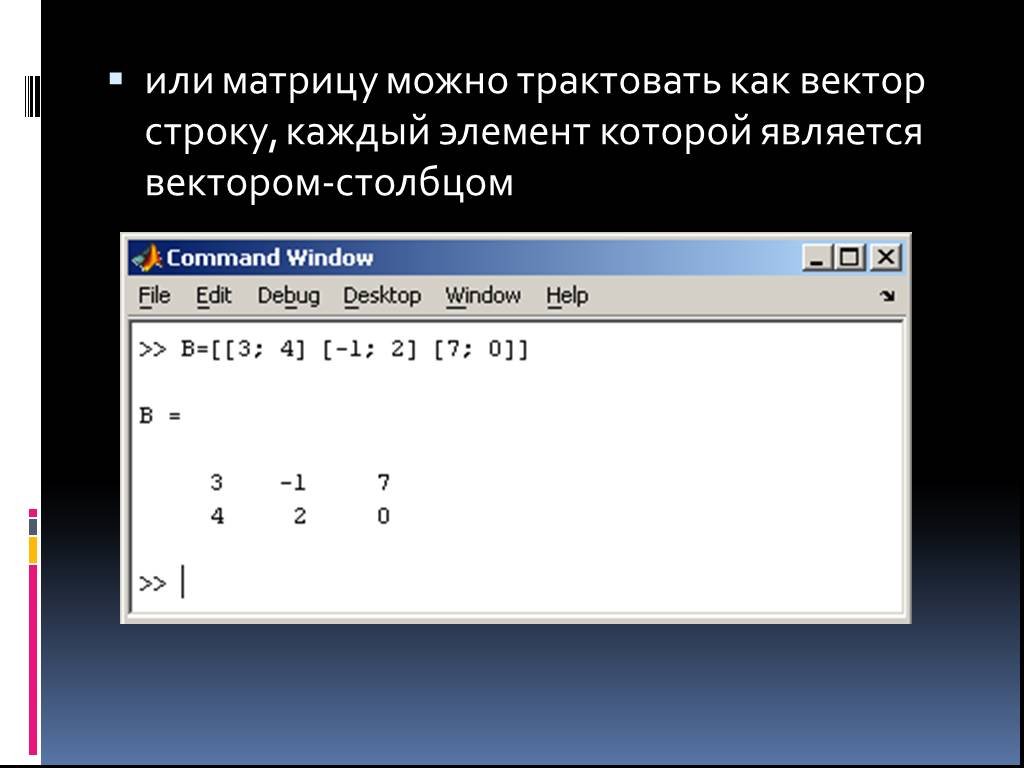
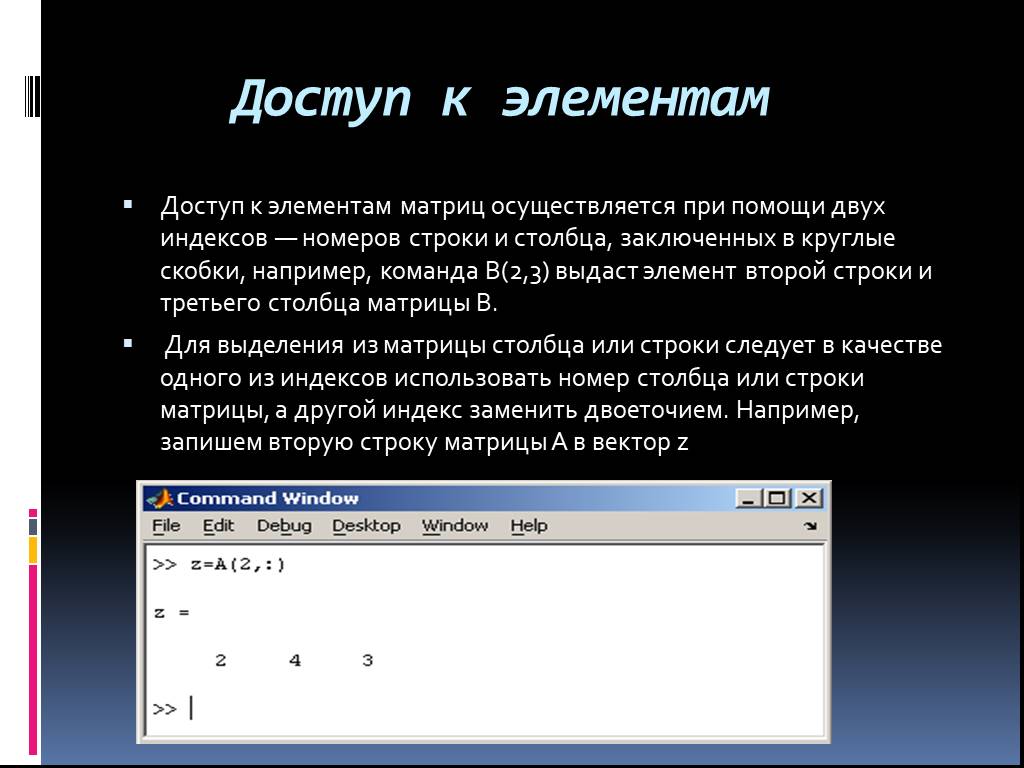
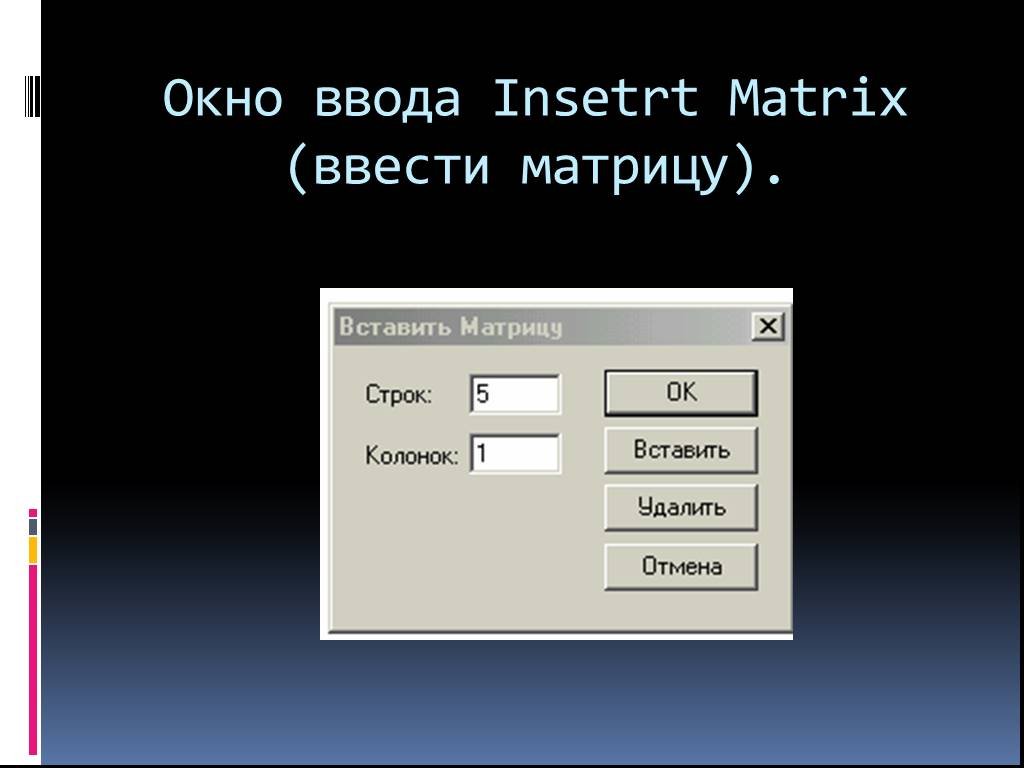
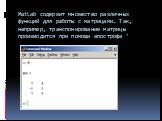
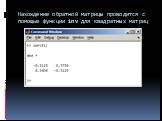
Интерактивная вычислительная система MathCad. . . . . . Wolfram Mathematica (WolframAlpha). Вычисление предела. Решение уравнения. Вычисление производной. ...Двоичное кодирование символьной информации
При двоичном кодировании текстовой информации каждому символу ставится в соответствие своя уникальная последовательность из восьми нулей и единиц, ...Социальная информатика и ее задачи
Социальная информатика – это наука, изучающая комплекс проблем, связанных с прохождением информационных процессов в социуме, это новое научное направление, ...Законы алгебры логики
Логическая формула-это выражение, содержащее логические константы, логические переменные, знаки логических операций. Логическая функция – зависимость ...Задачи программирования
Основной ресурс человечества. В современном мире в качестве основного ресурса на первое место выдвигается информация, средства и методы работы с ней. ...Задачи о рыцарях и лжецах
Задачи о рыцарях и лжецах — разновидность задач, в которых фигурируют персонажи: Лжец — человек (или иное существо), всегда говорящий ложь. Рыцарь, ...Задачи на кодирование текстовой информации и определение объема методика решения задач повышенного уровня сложности
Что следует знать:. чаще всего используют кодировки, в которых на символ отводится 8 бит (8-битные) или 16 бит (16-битные) необходимо запомнить, что ...Задачи на дроби
Цели:. Систематизировать, расширить и углубить знания, умения учащихся по изучаемой теме. Способствовать развитию наблюдательности, умения анализировать, ...Задачи компьютерной лингвистики
План:. 1.Что такое компьютерная лингвистика? 2. История. 3. Направления компьютерной лингвистики. 4. Заключение. Компьютерная лингвистика – это…. ...Компьютер школьного учителя математики
Первый выпуск журнала вышел 02 февраля 2010 года. Справа на странице находятся ссылки на все выпуски (23). В выпусках журнала, в основном, делается ...Задачи информационных систем в экономике
Задачи Информационных систем (ИС) в экономике. Основная задача ИС в экономике ‑ организация и эффективная обработка больших массивов данных в компьютеризированных ...Как устроена компьютерная сеть
Передача информации между ЭВМ и пользователем осуществляется через клавиатуру, дисплей, принтер и другие устройства ввода-вывода. А теперь мы узнаем, ...Физика + информатика
? Цель работы на уроке: исследовать объект окружающей среды средствами информатики и физики. «Человек без всякого воображения может собирать факты, ...Медицинская информатика
Термин ИНФОРМАТИКА возник в 60-х годах ХХ века во Франции для названия области, занимающейся автоматизированной переработкой информации, как слияние ...Социальная информатика
Отражает ли социальная информатика историю развития общества? Какой круг проблем является объектом изучения социальной информатики? Перечислите основные ...Современная компьютерная техника – взгляд изнутри
Типология современных компьютеров. Серверное оборудование Рабочие станции Ноутбуки Нетбуки Планшеты Моноблок. Классификация платформ. 32-битная платформа ...Прикладная информатика
Профессиональный стандарт. Исследователь в сфере ИТ - Computer and Information Scientist, Research Программист - Computer Programmer Системный архитектор ...Объекты и их свойства информатика
Объект растения явления природы животные фигуры. Общее в объектах. Различия между объектами. определяется их свойствами. Свойства имя значение. Русские ...Объекты и их свойства информатика
Объект - ЯБЛОКО красное круглое вкусное висит съедается продается зеленое кислое. о нем рассказывают. Объект - КНИГА листать читать. закрывать закладывать. ...Алгоритм и компьютерная программа
Компьютерная программа – алгоритм, записанный на одном из языков программирования. управляющее устройство, механизмы, которые помогают им двигаться. ...Конспекты
Решение задач математики средствами информатики
Урок ОВТ в 9 классе. (его можно провести после прохождения темы «Прогрессия»). . . Тема:. Решение задач математики средствами информатики. Цель:. ...Использование элементов алгебры логики при решении заданий ЕГЭ по информатике
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа № 2 п. Мостовского. муниципального образования Мостовский ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:31 марта 2019
Категория:Информатика
Классы:
Содержит:34 слайд(ов)
Поделись с друзьями:
Скачать презентацию




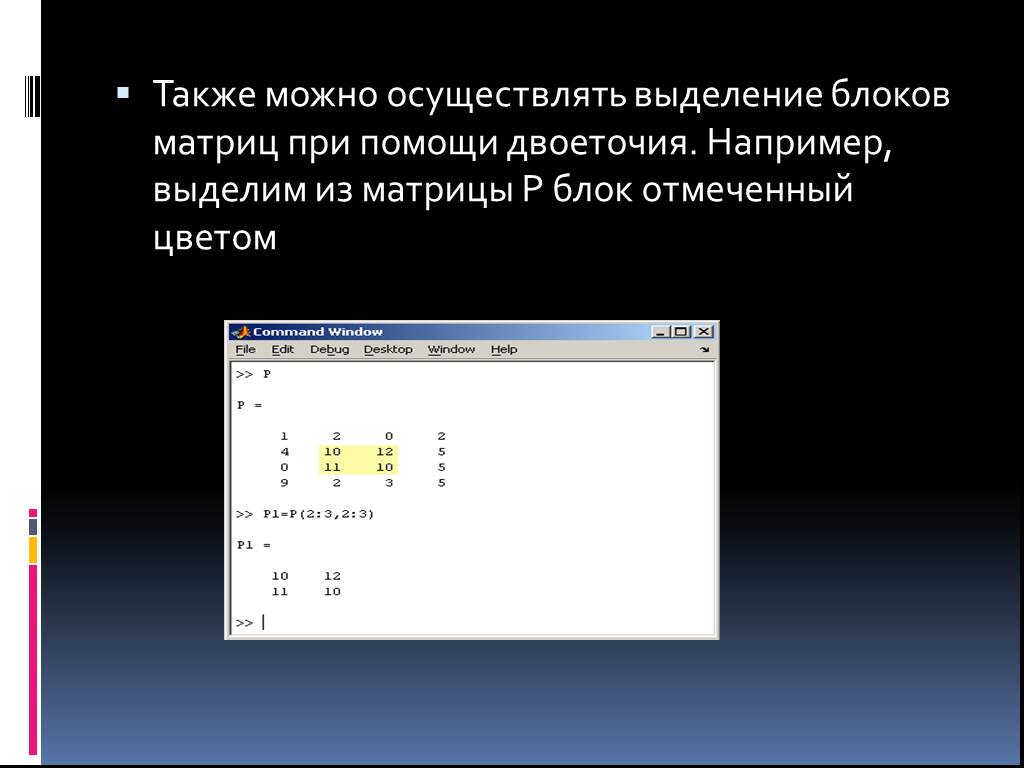


















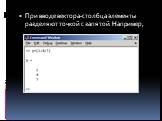
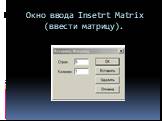




![Определение матрицы: matrix(n, m, [[a11,a12,…,a1n], [a21,a22,…,a2m],…,[an1,an2,…,anm]]), где n − число строк, m – число столбцов в матрице. Определение матрицы: matrix(n, m, [[a11,a12,…,a1n], [a21,a22,…,a2m],…,[an1,an2,…,anm]]), где n − число строк, m – число столбцов в матрице.](https://prezentacii.org/upload/cloud/19/03/137566/images/thumbs/screen27.jpg)
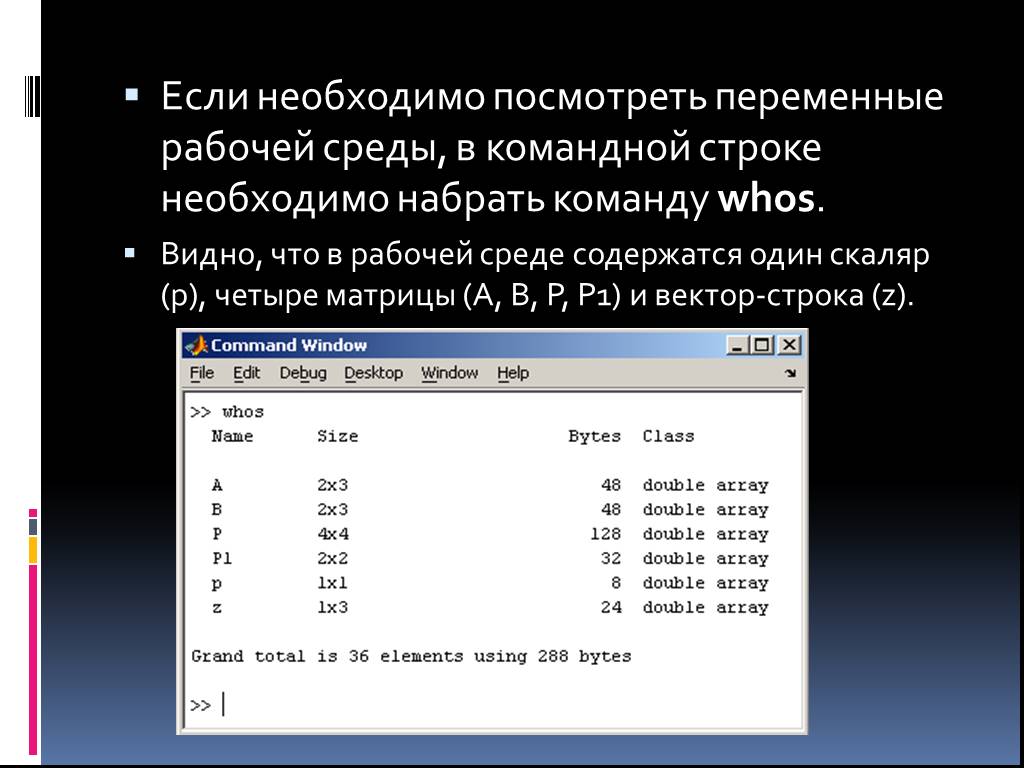
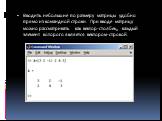
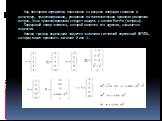
![Например: > A:=matrix([[1,2,3],[-3,-2,-1]]); A:= 1 2 3 -3 -2 -1 Например: > A:=matrix([[1,2,3],[-3,-2,-1]]); A:= 1 2 3 -3 -2 -1](https://prezentacii.org/upload/cloud/19/03/137566/images/thumbs/screen28.jpg)
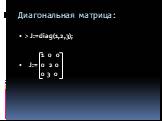


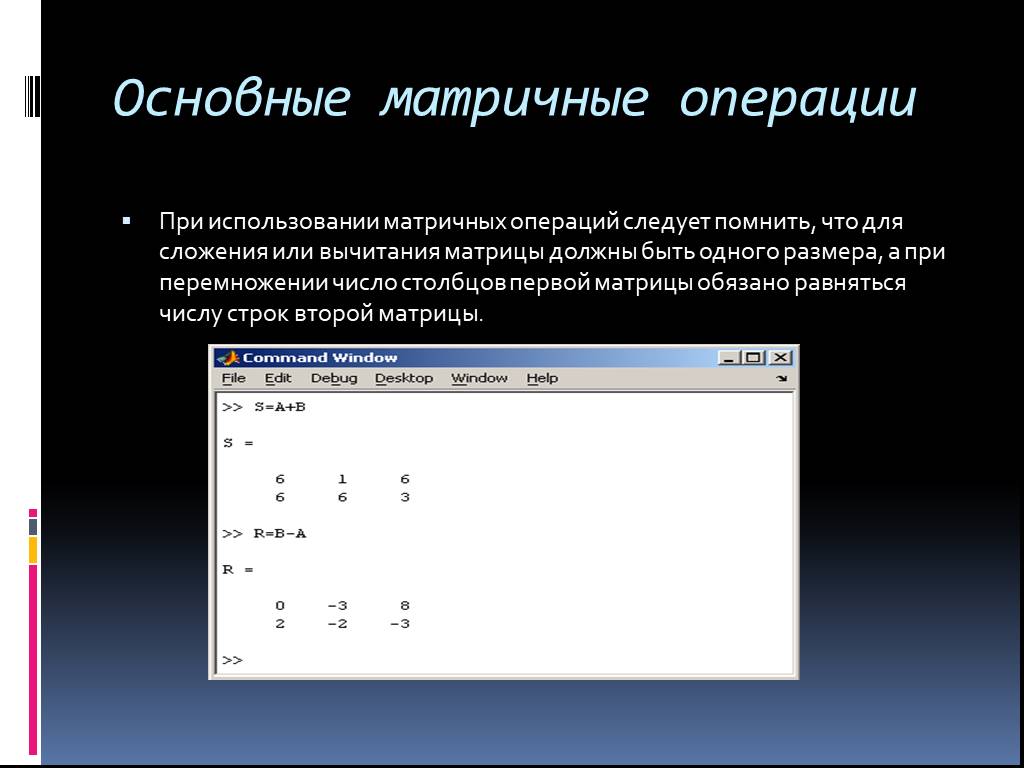
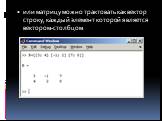
![В качестве второго аргумента в командах, вычисляющих произведение, можно указывать вектор, например: > A:=matrix([[1,0],[0,-1]]); > B:=matrix([[-5,1], [7,4]]); В качестве второго аргумента в командах, вычисляющих произведение, можно указывать вектор, например: > A:=matrix([[1,0],[0,-1]]); > B:=matrix([[-5,1], [7,4]]);](https://prezentacii.org/upload/cloud/19/03/137566/images/thumbs/screen32.jpg)
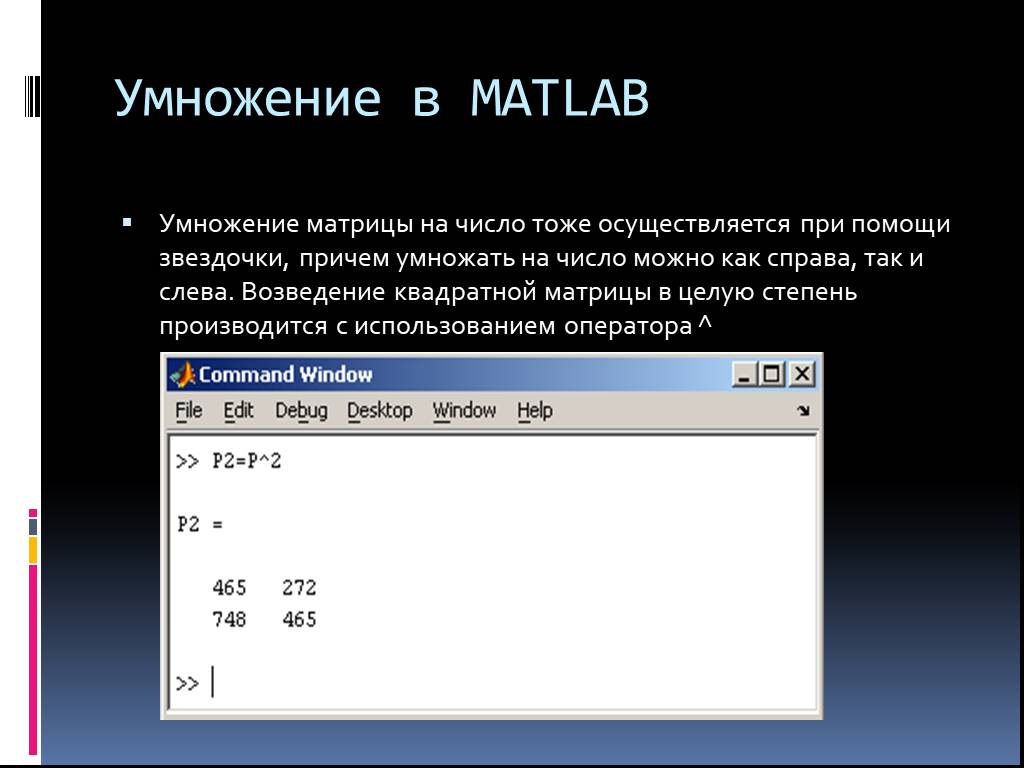
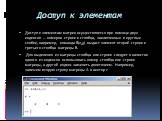
![A= 1 0 B:= -5 1 0 -1 7 4 >v:=vector([2,4]); >v := [2,4] multiply(A,v); [2,−4] A= 1 0 B:= -5 1 0 -1 7 4 >v:=vector([2,4]); >v := [2,4] multiply(A,v); [2,−4]](https://prezentacii.org/upload/cloud/19/03/137566/images/thumbs/screen33.jpg)
![multiply(A,B); matadd(A,B); -5 1 -4 1 -7 -4 7 3 Команда evalm позволяет также прибавлять к матрице число и умножать матрицу на число. Например: > С:=matrix([[1,1],[2,3]]): > evalm(2+3*С); 5 3 6 11 multiply(A,B); matadd(A,B); -5 1 -4 1 -7 -4 7 3 Команда evalm позволяет также прибавлять к матрице число и умножать матрицу на число. Например: > С:=matrix([[1,1],[2,3]]): > evalm(2+3*С); 5 3 6 11](https://prezentacii.org/upload/cloud/19/03/137566/images/thumbs/screen34.jpg)