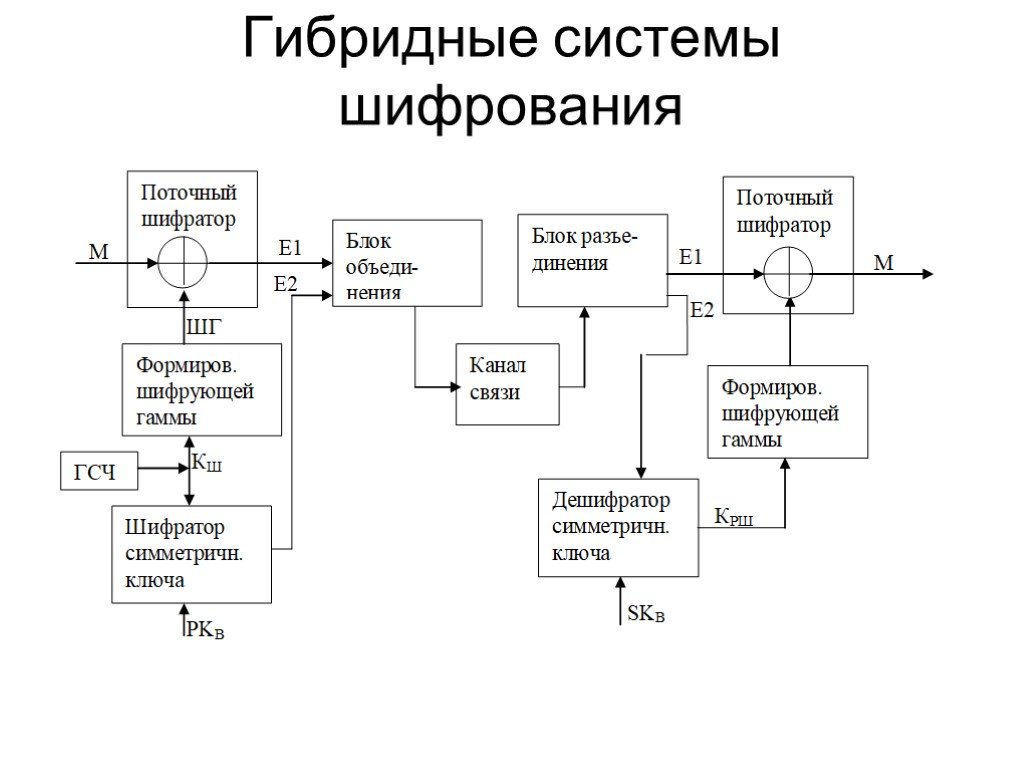
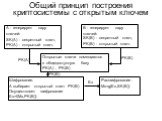
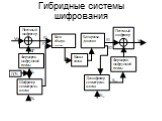
Презентация "Криптосистемы с открытым ключем" по информатике – проект, доклад
Презентацию на тему "Криптосистемы с открытым ключем" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Информатика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 19 слайд(ов).
Слайды презентации
Список похожих презентаций
Физика + информатика
? Цель работы на уроке: исследовать объект окружающей среды средствами информатики и физики. «Человек без всякого воображения может собирать факты, ...Социальная информатика и ее задачи
Социальная информатика – это наука, изучающая комплекс проблем, связанных с прохождением информационных процессов в социуме, это новое научное направление, ...Ты, я и информатика
I ТУР. Что изучает информатика? конструкцию компьютера способы представления, накопления, обработки и передачи информации с помощью технических средств ...Социальная информатика
Отражает ли социальная информатика историю развития общества? Какой круг проблем является объектом изучения социальной информатики? Перечислите основные ...Социальная информатика
Социальная информатика - это про что? Обратимся к предметной области Информатикa. Социальная информатика. Информационные ресурсы как фактор социально-экономического ...Прикладная информатика
Профессиональный стандарт. Исследователь в сфере ИТ - Computer and Information Scientist, Research Программист - Computer Programmer Системный архитектор ...Социальная информатика
Социальная информатика - это наука, изучающая комплекс проблем, связанных с прохождением информационных процессов в социуме. Один из основоположников ...Объекты и их свойства информатика
Объект растения явления природы животные фигуры. Общее в объектах. Различия между объектами. определяется их свойствами. Свойства имя значение. Русские ...Правовая информатика
Исполнение и цели. Правовая информатика – это междисциплинарная отрасль знания о закономерностях и особенностях информационных процессов в сфере юридической ...Объекты и их свойства информатика
Объект - ЯБЛОКО красное круглое вкусное висит съедается продается зеленое кислое. о нем рассказывают. Объект - КНИГА листать читать. закрывать закладывать. ...Медицинская информатика
Термин ИНФОРМАТИКА возник в 60-х годах ХХ века во Франции для названия области, занимающейся автоматизированной переработкой информации, как слияние ...Занимательный урок Фольклорная информатика
Разделы. Компьютерные добавлялки Слова с компьютерной начинкой Слова, оснащенные компьютером Попробуй прочитай Компьютерные анаграммы Словесное сложение ...Весёлая информатика
Эпиграф. Ты лишь на старте, длинен путь. Но к цели он ведет. И мир компьютеров тебя, Быть может, увлечет. А. М. Хайт. Цель:. развитие интереса к предмету, ...Бизнес информатика
Бизнес-информатика — междисциплинарное направление практической и теоретической деятельности, исследований и обучения, затрагивающее вопросы бизнес-управления, ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:19 февраля 2019
Категория:Информатика
Содержит:19 слайд(ов)
Поделись с друзьями:
Скачать презентацию