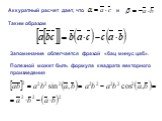Презентация "Векторы" по физике – проект, доклад

Лекция 2

Вектором называются величины, которые характеризуются численным значением и направлением, кроме того, складывающиеся по правилу параллелограмма, т.е. геометрически. Последнее замечание весьма существенно, поскольку существуют такие величины, которые характеризуются численным значением и направлением, однако, складываются иначе, чем векторы (псевдовекторы).

В Е К Т О Р Ы

Более строгое определение вектора: вектором называется совокупность трех величин

которые при переходе от одной системы координат к другой преобразуются по формулам

в которых коэффициенты имеют значения

Численное значение вектора называется его модулем, т.е. модуль дает длину вектора. Это уже величина ска- лярная, причем всегда положительная.

На чертежах векторы изображаются в виде прямолиней- ных отрезков со стрелкой на конце. Длина отрезка опре- деляет в установленном масштабе модуль вектора, а стрелка указывает направление вектора. Векторы принято обозначать буквами жирного шрифта (в книгах), либо со стрелочками наверху

Обычная буква используется для обозначения модуля вектора

Иногда для обозначения модуля используют символ

Для свободных векторов справедливо следующее определение равенства двух векторов: они коллинеарные, имеют одинаковое направление и совпадают по модулю.

Векторы, направленные вдоль параллельных прямых (в одну и туже или в противоположенные стороны), называются коллинеарными.

Векторы, которые лежат в параллельных плоскостях, называются компланарными.

Посредством параллельного переноса коллинеарные векторы могут быть расположены вдоль одной и той же прямой, а компланарные векторы могут быть сведены в одну плоскость.

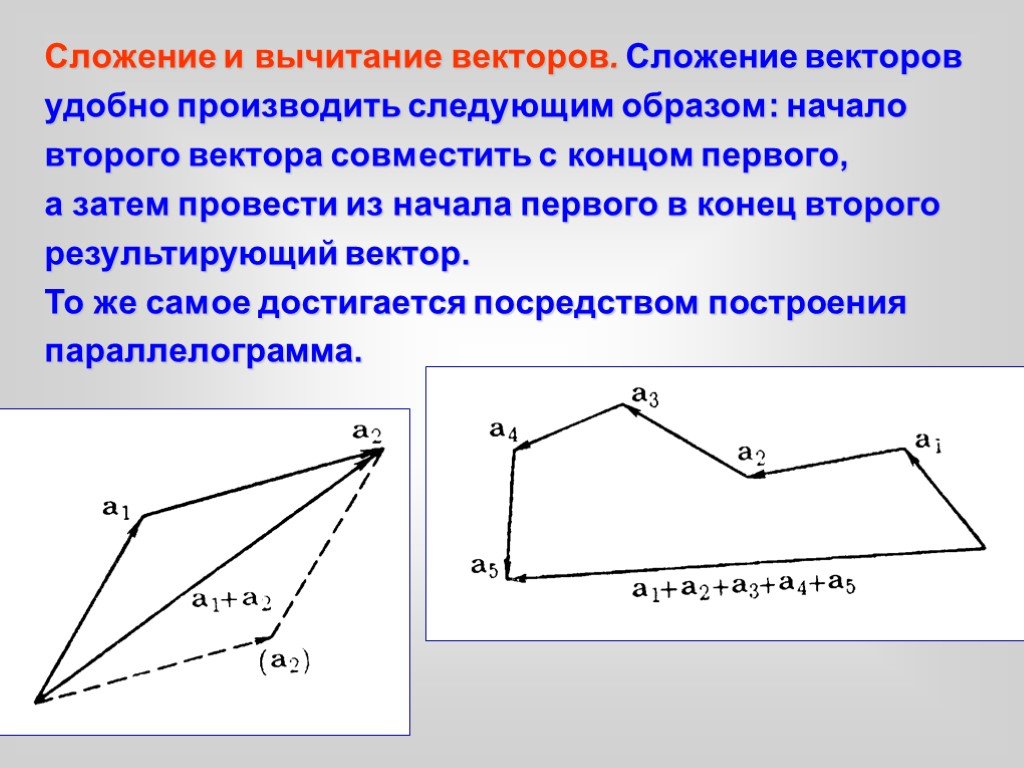
Сложение и вычитание векторов. Сложение векторов удобно производить следующим образом: начало второго вектора совместить с концом первого, а затем провести из начала первого в конец второго результирующий вектор. То же самое достигается посредством построения параллелограмма.

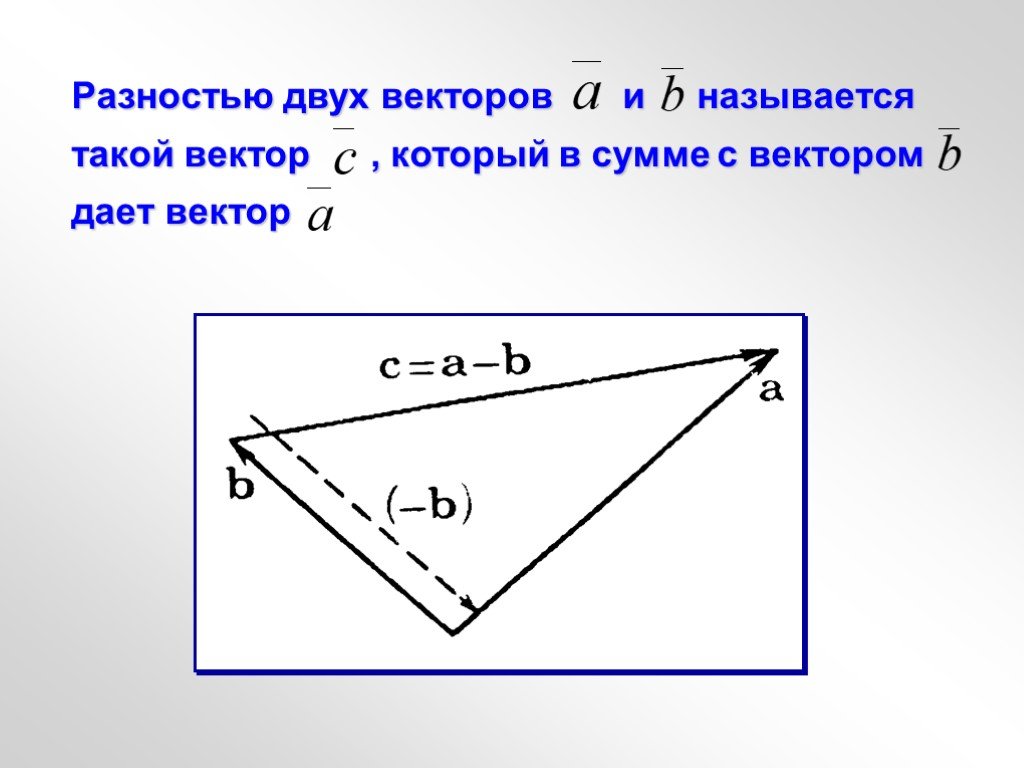
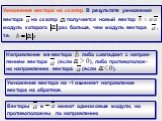
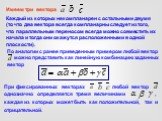
Разностью двух векторов и называется такой вектор , который в сумме с вектором дает вектор

Умножение вектора на скаляр. В результате умножения вектора на скаляр получается новый вектор модуль которого раз больше, чем модуль вектора , т.е.

Направление же вектора либо совпадает с направ-лением вектора (если ), либо противополож-но направлению вектора (если ).

Умножение вектора на -1 изменяет направление вектора на обратное.

Векторы и имеют одинаковые модули, но противоположны по направлению

Вектор называется единичным вектором или ортом вектора .

Вычитание из вектора вектора равнозначно прибавлению к вектору вектора .

Всякий вектор можно представить в виде

где - модуль вектора

вектор с модулем, равным единице, имеющим такое же направление, как и .

Орт можно представить в виде

откуда следует, что орт является безразмерной величиной.

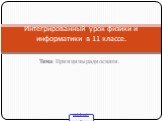
Орты можно сопоставлять не только векторам, но и любым направлениям в пространстве. Например:

- орт координатной оси ,

- орт нормали к кривой или поверхности,

- орт касательной к поверхности и т.д.

где и - некоторые числа.

Линейная зависимость между векторами. Рассмотрим три неколлинеарных вектора , и , которые лежат в одной плоскости.

Любой из них (например, ) можно выразить через два других с помощью соотношения

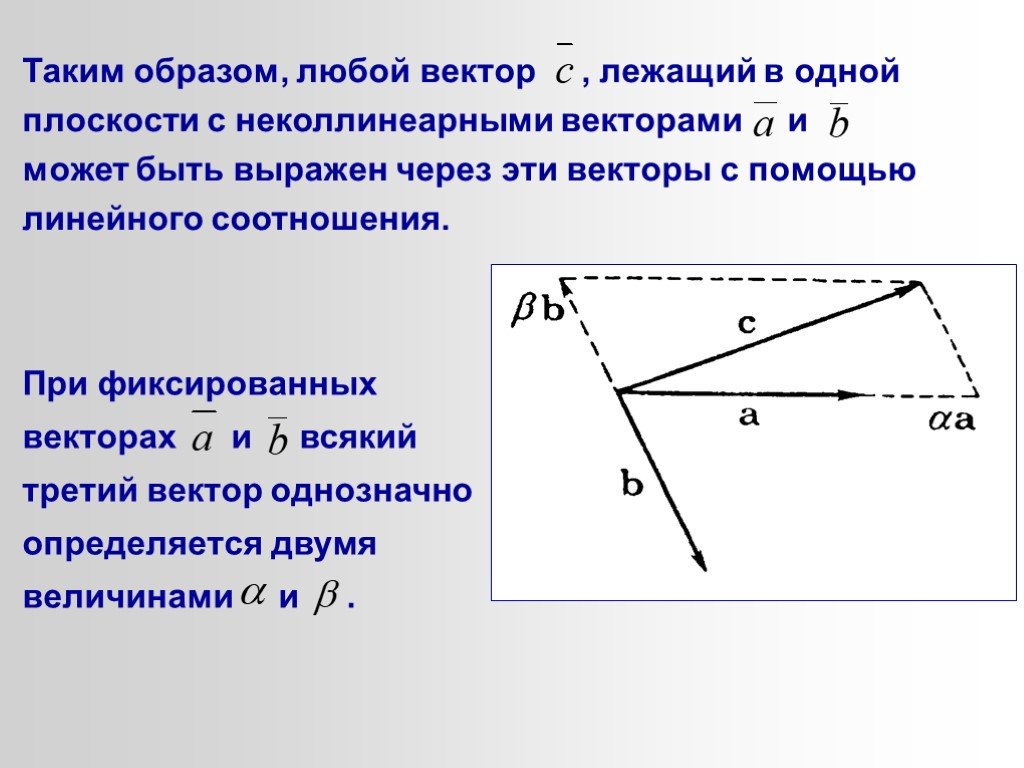
Таким образом, любой вектор , лежащий в одной плоскости с неколлинеарными векторами и может быть выражен через эти векторы с помощью линейного соотношения.

При фиксированных векторах и всякий третий вектор однозначно определяется двумя величинами и .

По аналогии с ранее приведенным примером любой вектор можно представить как линейную комбинацию заданных вектор

Имеем три вектора

Каждый из которых некомпланарен с остальными двумя (то что два вектора всегда компланарны следует из того, что параллельным переносом всегда можно совместить их начала и тогда они окажутся расположенными в одной плоскости).

При фиксированных векторах любой вектор однозначно определяется тремя величинами , каждая из которых может быть как положительной, так и отрицательной.

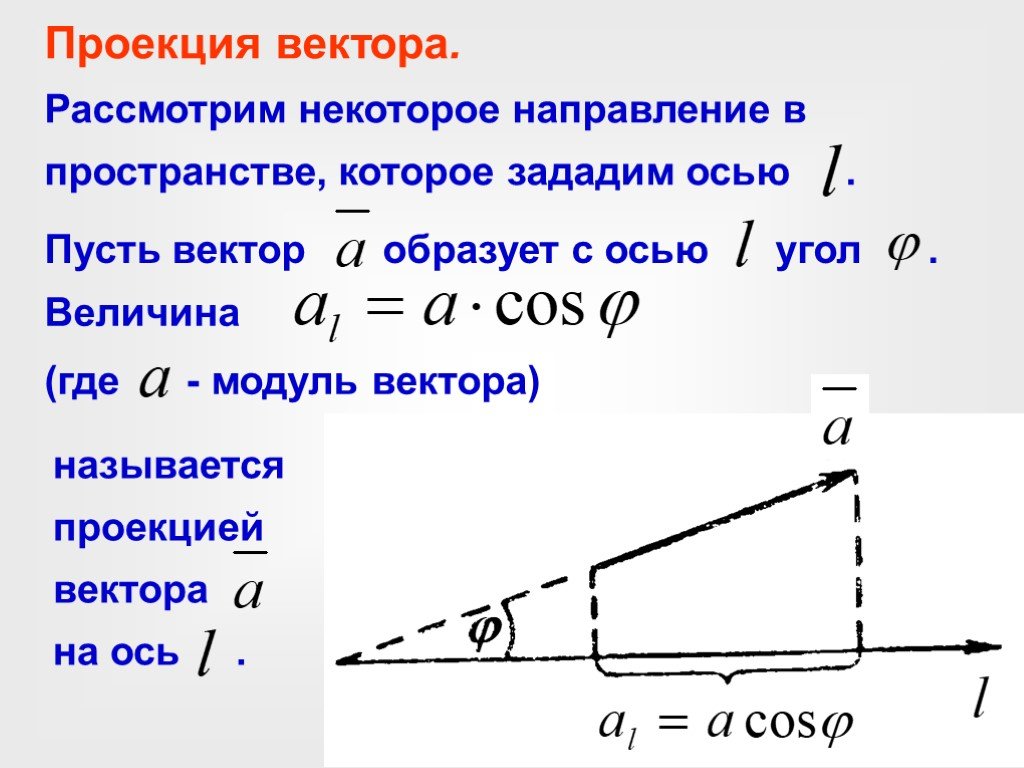
Проекция вектора. Рассмотрим некоторое направление в пространстве, которое зададим осью .

Величина

(где - модуль вектора)

называется проекцией вектора на ось .

Пусть вектор образует с осью угол .

Проекция вектора является величиной алгебраической. Если вектор образует с данным направлением острый угол, то , так что проекция положительная. Если угол тупой, и, следовательно, проекция отрицательна. Когда вектор перпендикулярен к данной оси, проекция равна нулю.

Геометрический смысл проекции вектора простой: она равна расстоянию между проекциями на ось начала и конца отрезка, изображающего данный вектор. В случае

это расстояние берется со знаком плюс. В случае

- со знаком минус.

Проекция результирующего вектора на некоторое направление равна сумме проекций складываемых векторов:

Пусть

При суммировании проекций изображенных на рисунке векторов расстояния 0-1, 1-2 и 2-3 нужно брать со знаком плюс, а расстояние 3-4 – со знаком минус.

Выражение вектора через его координатные оси. Возьмем декартовы оси координат и рассмотрим вектор лежащий в плоскости, перпендикулярной оси .

Введем орты координатных осей, т.е. единичные векторы и .

( на рисунке не показан, поскольку он направлен на нас).

Роль коэффициентов играют проекции вектора на оси координат.

Из рисунка видно, что вектор можно представить в виде

линейной комбинации ортов

Эта тройка ортов полностью определяет систему координат и поэтому называется базисом координатной системы.

Величины равны (с точностью до знака) сторонам прямоугольного параллелепипеда, большой диагональю которого служит вектор .

В общем случае, когда все три проекции вектора отличны от нуля

Таким образом, любой вектор можно выразить через его проекции на координатные оси и орты этих осей. В связи с этим проекции на координатные оси называются компонентами вектора.

Поэтому имеет место соотношение

(1)

Представив каждый из векторов в соответствии с формулой (1), получим:

На основании того, что равные векторы имеют равные проекции можно записать, что

(2)

Формулы (2) является аналитическим выражением правила сложения векторов и справедливы при любом числе слагаемых.

Радиус-вектор. Радиус-вектором некоторой точки называется вектор, проведенный из начала координат в данную точку. Его проекции на координатные оси равны декартовым координатам данной точки:

Следовательно, в соответствии с (1) радиус-вектор можно представить в виде

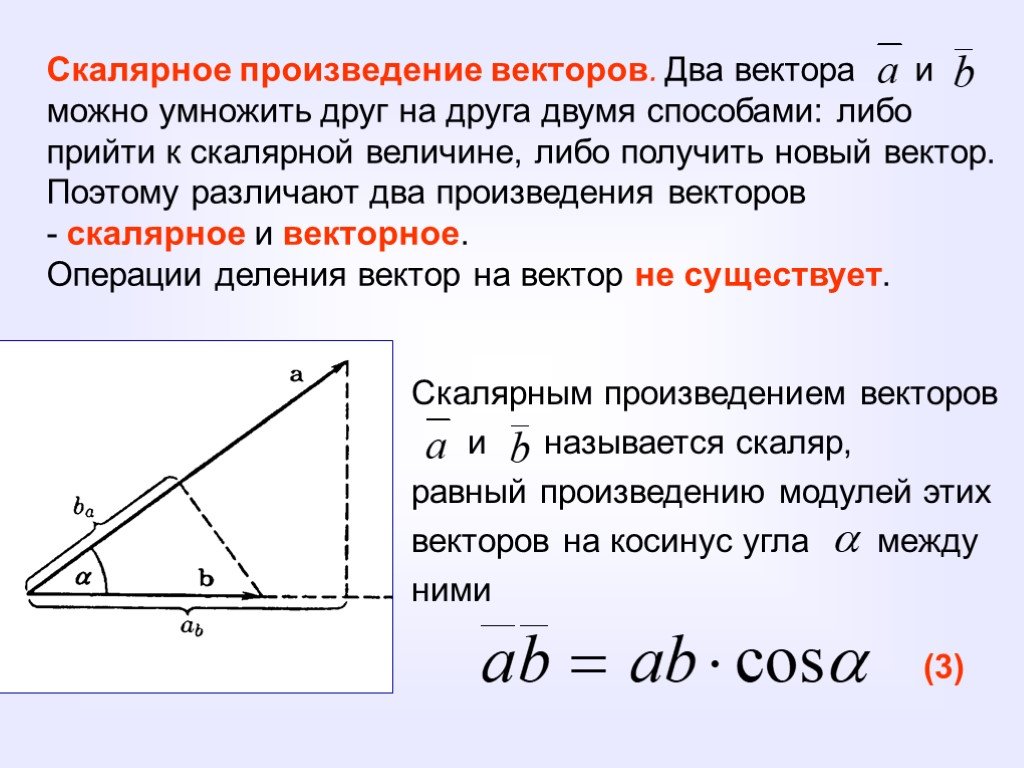
И согласно (2)

Скалярное произведение векторов. Два вектора и можно умножить друг на друга двумя способами: либо прийти к скалярной величине, либо получить новый вектор. Поэтому различают два произведения векторов скалярное и векторное. Операции деления вектор на вектор не существует.

Скалярным произведением векторов и называется скаляр, равный произведению модулей этих векторов на косинус угла между ними

(3)

Выражение (3) является алгебраической величиной: при остром ; при тупом .

Скалярное произведение взаимно перпендикулярных векторов равно нулю.

Квадрат вектора - скалярное произведение вектора на самого себя

Квадрат вектора равен квадрату его модуля. В частности, квадрат любого орта равен единице:

Вследствие взаимной перпендикулярности ортов, скалярные произведения вида равны нулю, если

Удобным в использовании является символ Кронекера

Используя этот символ, скалярное произведение ортов координатных осей можно выразить одной формулой

Скалярное произведение коммутативно, т.е. не зависит от порядка сомножителей

Оно может быть записано несколькими способами

Используя определение проекции одного вектора на направление другого вектора, имеем

Приняв во внимание, что проекция суммы векторов равна сумме проекций складываемых векторов, можно записать

Таким образом, скалярное произведение векторов дистрибутивно – произведение вектора на сумму нескольких векторов равно сумме произведение вектора на каждый из слагаемых векторов, взятый в отдельности.

Важный вывод - изменения проекций векторов и при поворотах осей носят такой характер, что их комби- нация вида (4) остается инвариантной (неизменной):

Заметим, что при поворотах координатных осей проекции векторов на эти оси меняются. Однако, величина

от выбора осей не зависит.

Воспользовавшись дистрибутивностью скалярного произведения и символом Кронекера, получим выраже- ние скалярного произведения через проекции векторов

(4)

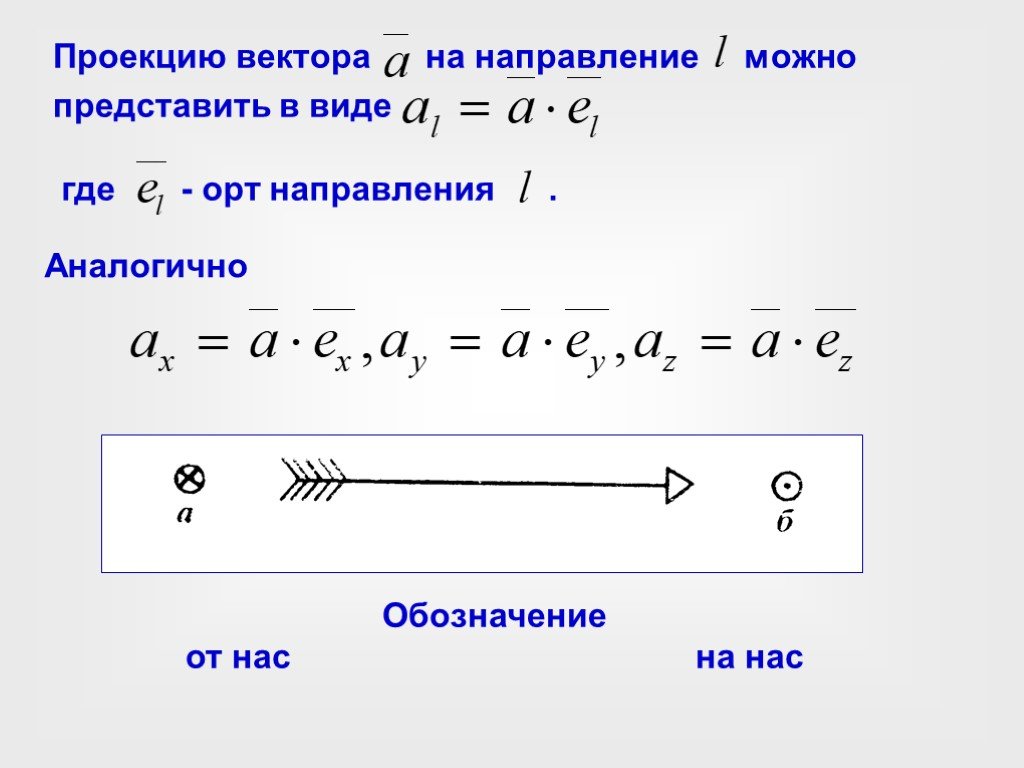
Проекцию вектора на направление можно представить в виде

где - орт направления .

Аналогично

Обозначение от нас на нас

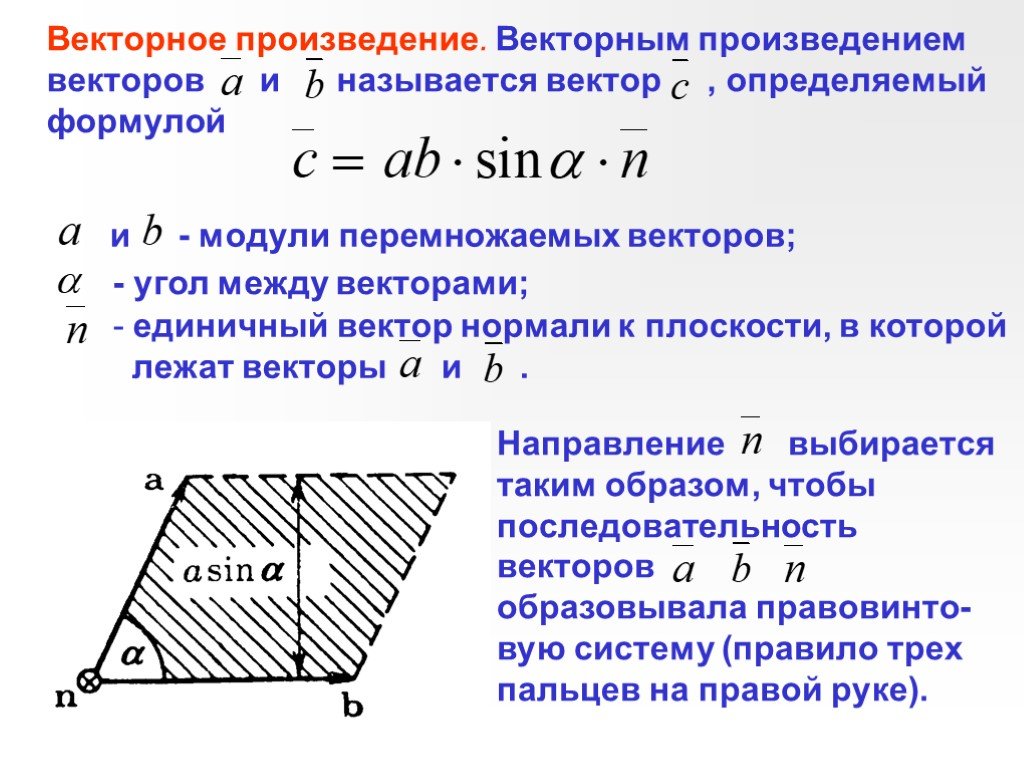
Векторное произведение. Векторным произведением векторов и называется вектор , определяемый формулой

и - модули перемножаемых векторов;

- угол между векторами;

единичный вектор нормали к плоскости, в которой лежат векторы и .

Направление выбирается таким образом, чтобы последовательность векторов образовывала правовинто-вую систему (правило трех пальцев на правой руке).

Это означает, что если смотреть вслед вектору , то совершаемый по кратчайшему пути поворот от первого сомножителя ко второму осуществляется по часовой стрелке. На рисунке вектор направлен за чертеж и изображен кружком с крестиком. Направление вектора совпадает с направлением .

Символически векторное произведение записывается или

Таким образом, векторное произведение

Модуль векторного произведения имеет простой геометрический смысл. Выражение численно равно площади параллелограмма, построенного на перемножаемых векторах.

(5)

При рассмотрении таких векторов, как радиус-вектор , скорость , сила и т.п., вопрос о выборе их направ- ления не возникает - оно вытекает естественным образом из природы самых величин. Подобные векторы называются истинными (или полярными).

Направление вектора определено, связав его с направ- лением вращения от первого сомножителя ко второму.

Векторы типа направление которых связывается с направлением вращения, называются псевдовекторами (или аксиальными векторами). При изменении условий, например при переходе от правой системы координат к левой (инверсия системы координат), направления псевдовекторов изменяются на обратные, истинные же векторы при этом остаются без изменений.

Небольшое отступление

Следует иметь в виду, что векторное произведение будет псевдовектором только в том случае, когда оба перемножаемых вектора являются истинными (или оба – псевдовекторами).

Изменение условия, определяющего направление псевдовекторов, на обратное приведет в этом случае к изменению знака перед векторным произведением и одновременно к изменению знака перед одним из сомножителей. В итоге величина, выражаемая векторным произведением, останется без изменений.

Векторное же произведение истинного вектора на псевдовектор будет истинным вектором.

Поскольку направление векторного произведения определяется направлением вращения от первого сомножителя ко второму, результат векторного перемножения зависит от порядка сомножителей. Перестановка сомножителей вызывает изменение направления результирующего вектора на противоположное. Таким образом, векторное произведение не обладает свойством коммутативности:

Векторное произведение дистрибутивно, т.е.

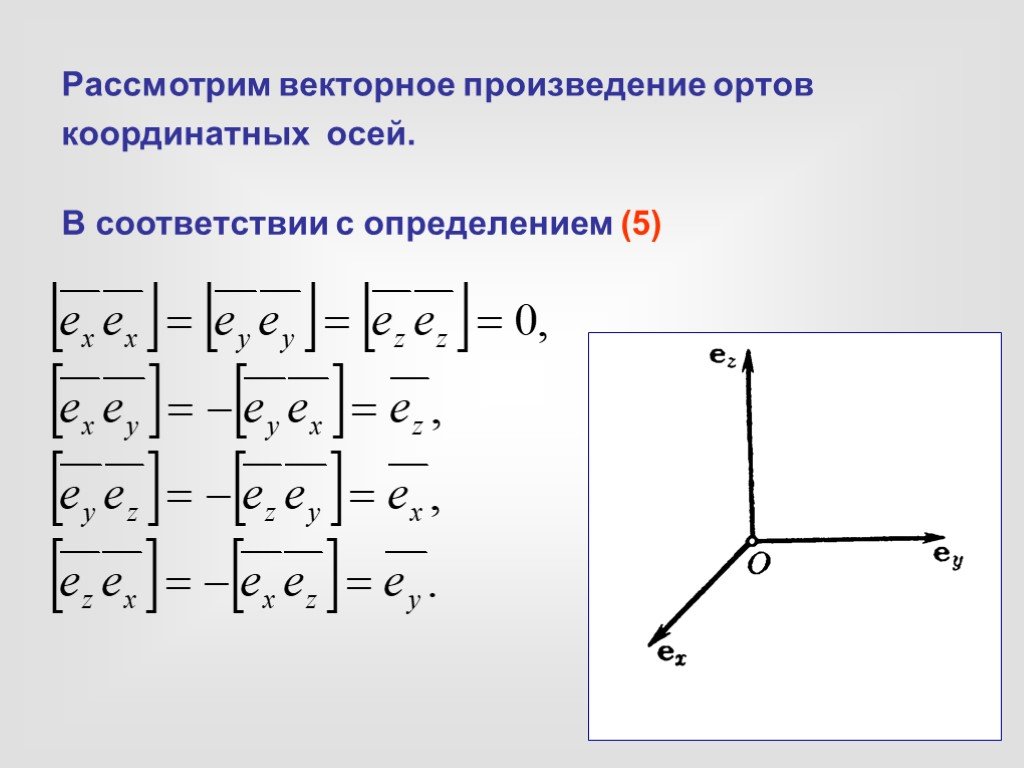
Рассмотрим векторное произведение ортов координатных осей.

В соответствии с определением (5)

Запишем перемножаемые векторы в виде

и

Теперь воспользуемся свойством дистрибутивности

Это же выражение можно представить в виде определителя:

Выражение имеет простой геометрический смысл – оно численно равно объему паралле- лепипеда, построенного на перемножаемых векторах (взятому со знаком плюс или минус в зависимости от величины угла ).

Смешанное произведение. Смешанным (или скалярно- векторным) произведением трех векторов называется выражение т.е. скалярное произведение вектора на векторное произведение векторов и .

Согласно определению

При вычислении объема параллелепипеда результат не может зависеть от того, какая из его граней взята в качестве основания. Отсюда следует, что

Смешанное произведение допускает циклическую перестановку сомножителей, т.е. замену каждого из сомножителей следующим за ним в цикле.

Двойное векторное произведение. Рассмотрим двойное векторное произведение трех векторов

Всякое векторное произведение перпендикулярно к обоим сомножителям. Поэтому вектор перпендику- лярен к орту , определяющему направление вектора .

Отсюда вытекает, что вектор лежит в плоскости, образованной векторами и и, следовательно, может быть представлен как линейная комбинация этих векторов:

Аккуратный расчет дает, что

Таким образом

Запоминание облегчается фразой «бац минус цаб».

Полезной может быть формула квадрата векторного произведения

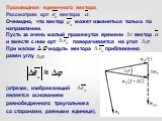
Кинематические величины

Производная вектора. Рассмотрим вектор, который изменяется со временем по известному закону

Проекции этого вектора на координатные оси представляют собой заданные функции времени, т.е.

(здесь предполагается, что нет пространственного изменения орт осей!!!).

Пусть за промежуток времени проекции вектора получают приращения

Тогда вектор получит приращение

Скорость изменения вектора со временем можно охарактеризовать отношением к

(6)

Это отношение дает среднюю скорость изменения в течение промежутка времени .

Чем меньше этот промежуток времени, тем точнее величина (6) характеризует скорость изменения в момент времени , который предшествует интервалу времени .

В физике принято производные по времени обозначать символом соответствующей величины с точкой над ним, например:

и т.д.

Воспользовавшись таким обозначением, формуле (7) можно придать вид

Устремляя к нулю, получаем предел, который называется производной. Поэтому выражение (6) можно преобразовать к

(7)

Если в качестве взять радиус-вектор движущейся точки, то

где есть функции от :

Согласно определению дифференциалом («приращением») функции называется выражение

где - производная по .

В пределе при приближенное равенство переходит в точное.

Тогда дифференциал вектора можно определить как

И в частности

Заметим, что приращение функции за очень малый, но конечный промежуток времени приближенно равно

Аналогичную формулу можно записать и для векторной функции

(8) (9)

Производная произведения функции. Рассмотрим функцию , которая равна произведению скалярной функции на векторную функцию .

или

Найдем приращение искомой функции

Представив приращения функций в виде (8) и (9), получим

откуда

В пределе при это приближенное равенство превращается в точное.

Первые два слагаемые не зависят от

Предел третьего слагаемого равен нулю. Поэтому

Рассмотрим скалярное произведение двух векторных функций и

Приращение этого произведения равно:

Отсюда (10)

Умножая (10) на , переходим к дифференциалу

(11)

Вычислим производную и дифференциал квадрата векторной функции. Используя (10) и (11), имеем

Но из скалярного произведения векторов имеем

Тогда

Рассмотрим теперь производную векторного произведения функций и

Распишем приращение рассматриваемой функции

Соответственно

Осуществив предельный переход, придем к формуле

Производная единичного вектора. Рассмотрим орт вектора .

Очевидно, что вектор может изменяться только по направлению.

Пусть за очень малый промежуток времени вектор и вместе с ним орт поворачивается на угол

При малом модуль вектора приближенно равен углу

(отрезок, изображающий является основанием равнобедренного треугольника со сторонами, равными единице).

Заметим, что чем меньше , тем точнее соблюдается написанное приближенное равенство. Сам вектор можно представить в виде

При стремлении к нулю орт будет поворачиваться и в пределе совпадет с перпендикулярным к единичным вектором .

где - орт вектора

есть угловая скорость вращения вектора .

Орт лежит в той плоскости, в которой поворачи- вается в данный момент вектор , причем направлен в ту сторону, в которую происходит вращение.

Производная по согласно определению равна

Таким образом,