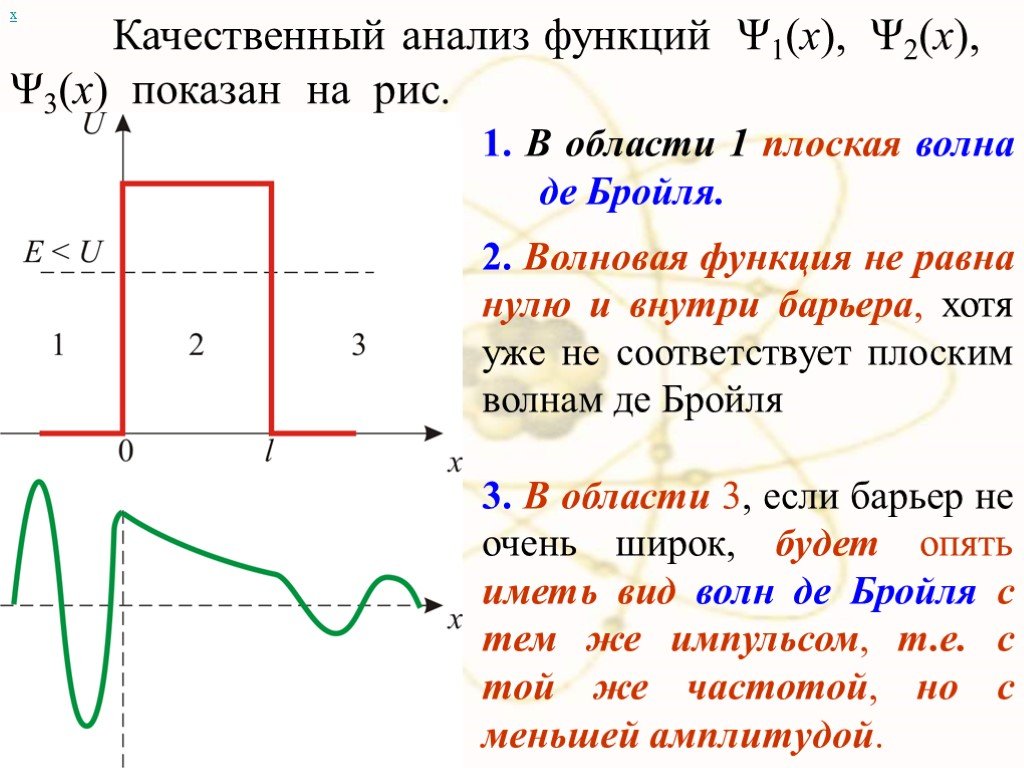
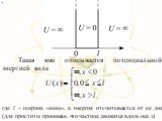
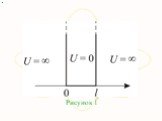
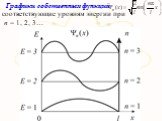
Презентация "Движение частицы" по физике – проект, доклад
Презентацию на тему "Движение частицы" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 42 слайд(ов).
Слайды презентации
Список похожих презентаций
Решение задач на движение частицы в магнитном поле.
1. Действует ли сила Лоренца:. на незаряженную частицу в магнитном поле; на заряженную частицу, покоящуюся в магнитном поле; на заряженную частицу, ...Фундаментальные элементарные частицы
Тест. 1.Какие физические системы образуются из элементарных частиц в результате электромагнитного взаимодействия? А. Электроны, протоны. Б. Ядра атомов. ...Использование теоретических знаний по теме: Движение тела в поле тяготения Земли в военной науке баллистике.
Содержание. Понятие – баллистики. История возникновения баллистики . Основные законы баллистического движения. Исследование баллистического движения ...Движение частиц вещества
Основные положения МКТ. Все вещества состоят из частиц, между которыми есть промежутки. Частицы находятся в хаотичном, непрерывном движении. Частицы ...Диффузия. Движение молекул
На территории современной Италии примерно III тысячи лет назад жили этруски – таинственный древний народ. Примерно к середине I тысячелетия до нашей ...Движение - в самом общем виде- изменение вообще
Из словаря русского языка С.И. Ожегова. В философии : форма существования материи, непрерывный процесс развития материального мира (нет материи без ...Движение урок
Цель урока: cформировать понятие механического движения. Задачи урока: cформировать у учащихся представление об относительности движения и покоя. ...Движение молекул
МОЛЕКУЛЯРНАЯ ФИЗИКА ТЕРМОДИНАМИКА. Т П У. Доцент кафедры Общей физики Кузнецов Сергей Иванович. Тема 3. ЭЛЕМЕНТЫ ФИЗИЧЕСКОЙ КИНЕТИКИ. 3.1. Явления ...Движение по окружности
…нам не стыдно признать, что весь подлунный мир и центр Земли движутся по Великому кругу между другими планетами, заканчивая свое обращение вокруг ...Движение и его характеристики
Механическое движение. Траектория. Путь. Равномерное движение. Неравномерное движение. Скорость. План. Механическое движение. Механическое движение ...Движение молекул
Движение молекул. 10.12.2017. Автор: Фоминова Елена Владимировна, учитель физики и информатики МБОУ СОШ № 23 МО Усть-Лабинский район хутора Братского ...Движение и взаимодействие тел
Цели урока. Образовательные: 1. Связанные с формированием общенаучных знаний - повторить понятия: движение, виды движения, путь, скорость, время; ...Движение заряженных частиц в электрическом и магнитном полях
Задача №1 Протон, влетая в электрическое поле напряженностью Е, прошел расстояние L и отклонился от положения равновесия на h метров. Найти скорость ...Движение заряженных частиц в магнитном поле
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца Х.Лоренц великий голландский физик, основатель ...Элементарные частицы
Цель:. Ознакомление с физикой элементарных частиц и систематизация знаний по теме. Развитие абстрактного, экологического и научного мышления учащихся ...Движение по окружности
Содержание. Виды криволинейного движения Основные характеристики движения по окружности ИСЗ. Виды криволинейного движения. Характеристики. Период ...Элементарные частицы атома
Этап второй. От позитрона до кварков: 1932—1964 гг. Ни одна из частиц не бессмертна. Большинство частиц, называемых сейчас элементарными, не может ...Движение под действием нескольких сил
Алгоритм решения задач Движение по горизонтали Движение по вертикали Движение по наклонной плоскости Движение связанных тел Движение по окружности ...Движение точки и тела. Положение точки в пространстве
Проверка домашнего задания. Сообщение о Ньютоне ( подготовленное учеником). Экспресс- опрос:. 1. Что такое механика? 2. На какие разделы подразделяют ...Движение под углом к горизонту
Условия задачи. Тело брошено со скоростью V под углом @ к горизонту. Определить: Траекторию движения тела Время полёта Дальность полёта Максимальную ...Конспекты
Сила Лоренца. Движение заряженной частицы в магнитных полях
Урок по физике в 10 классе по теме " Сила Лоренца. Движение заряженной частицы в магнитных полях». . Цель урока. : изучение действия магнитного ...Прямолинейное и криволинейное движение. Движение тела по окружности
МБОУ «Чубаевская ООШ» Урмарского района ЧР. УРОК ФИЗИКИ в 9 КЛАССЕ. «Прямолинейное и криволинейное движение. . . Движение тела по ...Сила всемирного тяготения. Движение тел под действием силы тяжести
План №______. Класс 9. Тема:. Сила всемирного тяготения. Движение тел под действием силы тяжести. . . Тип урока:. комбинированный. Цели:. ...Диффузия. Движение молекул. Броуновское движение
Тема:. . Диффузия. Движение молекул. Броуновское движение. . . Класс:. 7. . Цель урока. . Учащиеся должны усвоить знания о характере движения ...Закон всемирного тяготения. Движение в гравитационном поле.
Муниципальное бюджетное общеобразовательное учреждение. . средняя общеобразовательная школа №70 г. Липецка. План-конспект урока по физике. ...Движение тела, брошенного под углом к горизонту
Урок физики в 10 классе. . учителя физики и математики Запорожец Ольги Витальевны. КГУ «Новосветловской средней школы». СКО, Айыртауский район, ...Действие магнитного поля на движущиеся заряженные частицы
План-конспект урока. в 11 классе. по теме « Действие магнитного поля на движущиеся заряженные частицы». тип урока. : комбинированный. методы:. ...Движение тела по окружности. Искусственные спутники Земли
Разработка открытого урока в 9 классе. Тема: Движение тела по окружности. Искусственные спутники Земли. Разработала и провела:. учитель ...Движение тела, брошенного под углом к горизонту
МОБУ «Волховская городская гимназия». Разработка урока по физике с использованием. виртуального моделирующего эксперимента. Тема урока:. ...Движение тела по окружности с постоянной по модулю скоростью
. Автор:. Александрова Зинаида Васильевна, учитель физики и информатики. . Образовательное учреждение:. МОУ СОШ №5 п.Печенга, Мурманская обл. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 мая 2019
Категория:Физика
Содержит:42 слайд(ов)
Поделись с друзьями:
Скачать презентацию