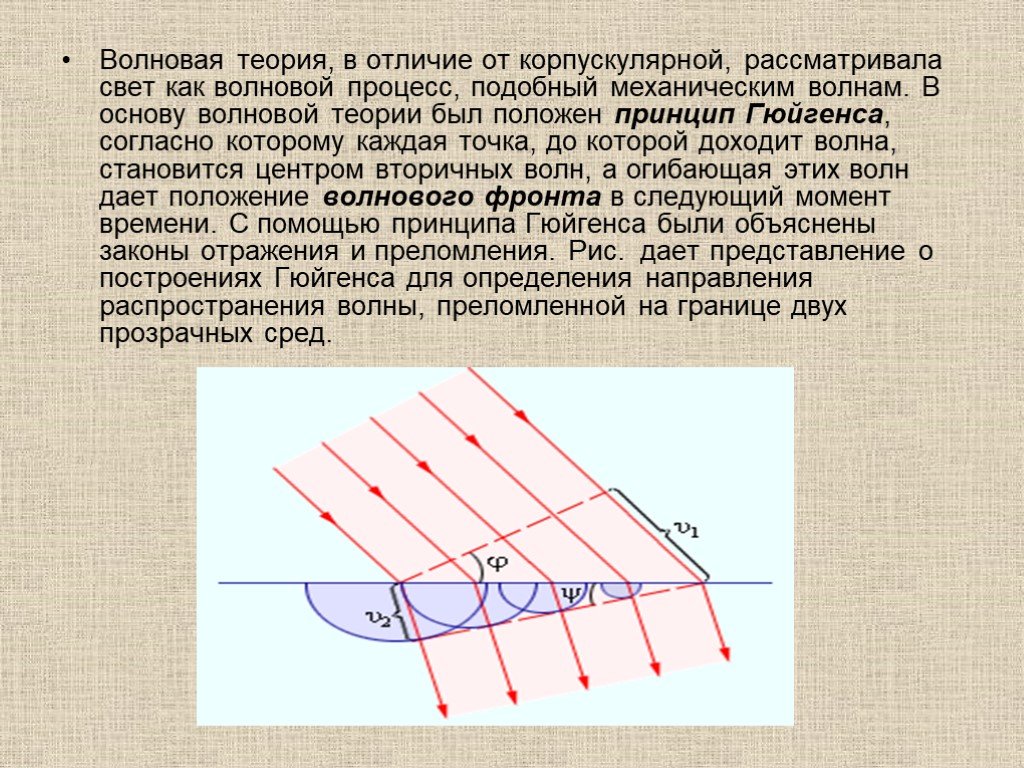
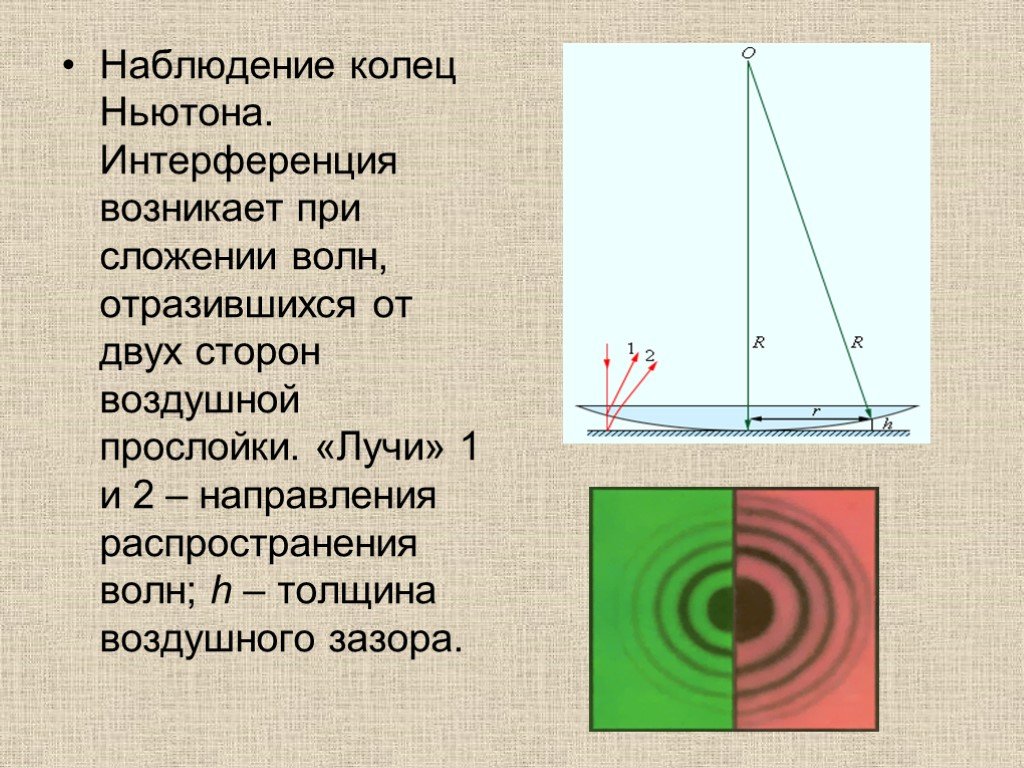
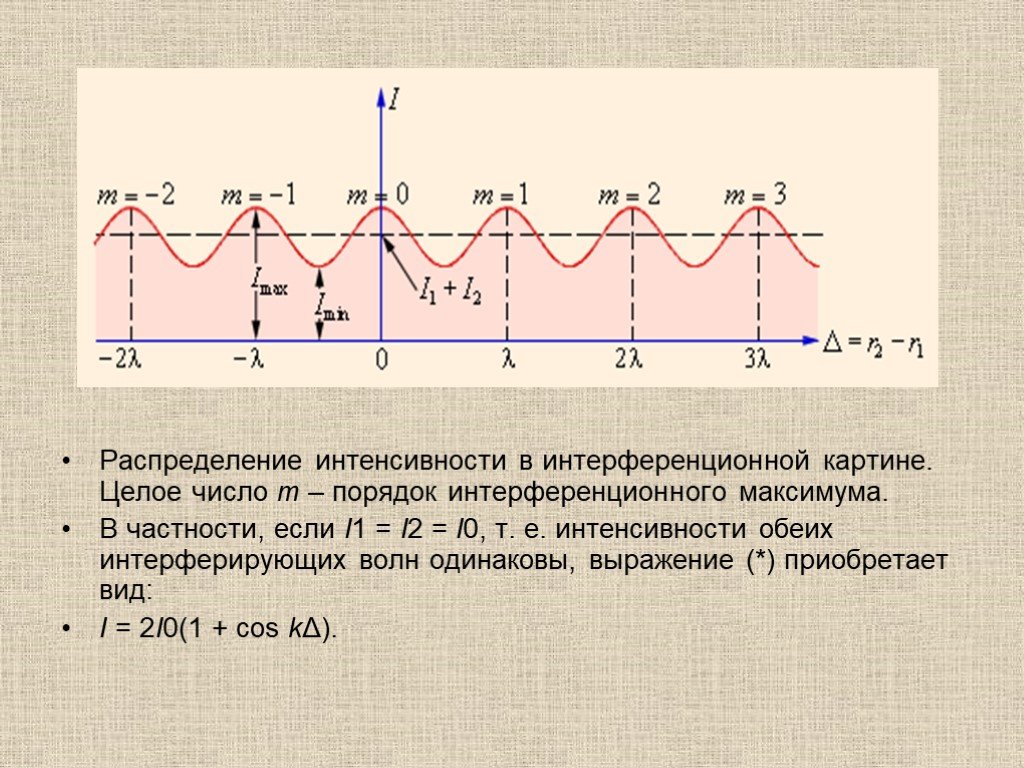
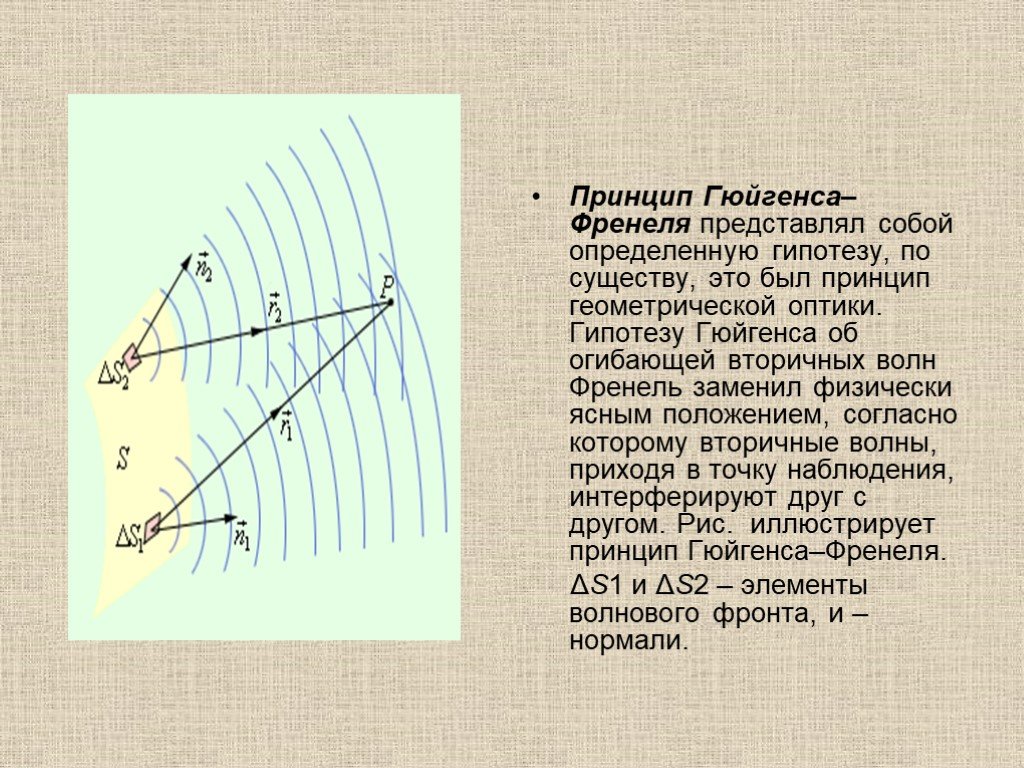
Презентация "Оптика" по физике – проект, доклад
Презентацию на тему "Оптика" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Физика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 30 слайд(ов).
Слайды презентации
Список похожих презентаций
Оптика свет
Геометрическая оптика – это раздел оптики изучающий законы распространения света в прозрачной среде на основе представления о свете как совокупности ...Оптика Световые явления и законы
Содержание. Свет - это электромагнитная волна Солнце – естественный источник света Закон распространения света Маяк Закон отражения света Отражения ...Оптика и свет
Свет. - это электромагнитные волны, воспринимаемые человеческим глазом. Он обладает квантово-волновым дуализмом, являясь одновременно электромагнитными ...Оптика Ломоносова
Цель данного проекта:. привлечь внимание учащихся к основам естественных наук, выяснить практическую ценность изучаемых явлений с использованием исторического ...Оптика и атомная физика
В основу настоящего конспекта лекций положен курс лекций по оптике, разработанный профессором кафедры оптики Н.К. Сидоровым и заведующим кафедры оптики ...Оптика и ее основы
Оптика – учение о природе света, световых явлениях и взаимодействии света с веществом. И почти вся ее история – это история поиска ответа: что такое ...Оптика
Другая точка зрения заключалась в том, что лучи испускаются светящимся телом и, достигая человеческого глаза, несут на себе отпечаток светящегося ...Оптика optics
Определение. OPTICS is a section of physics which learns the spreading of light and it’s interaction with substance. ОПТИКА – раздел физики, изучающий ...Оптика
ГИПОТЕЗА ПЕЛЛУЦИДА. СИСТЕМЫ ПЛОСКИХ ЗЕРКАЛ (античная оптика). Аристотель считал свет проявлением некоей разряженной среды, называемой пеллуцид и заполняющей ...Оптика
Роль зеркал в жизни человека, в быту и технике. Отражение света α = 90 Зеркало. Типы отражений света. Зеркальное отражение. Диффузное отражение. Что ...Оптика
Оптика – раздел физики, изучающий свойства и физическую природу света, а также его взаимодействие с веществом. Учение о свете принято делить на три ...Оптика
Оптика Источники света Фотометрия Световой поток Световой пучок. Световой луч. Сила света. Освещенность. Нормы освещенности. содержание. Раздел физики, ...Оптика
Науку все глубже постигнуть стремись, Познанием вечного жаждой томись. Лишь первых познаний блеснет тебе свет, Узнаешь: предела для знания нет. Фирдоуси ...Геометрическая оптика
Цель: повторение основных понятий, законов и формул ОПТИКИ в соответствии с кодификатором ЕГЭ. Элементы содержания, проверяемые на ЕГЭ 2010: Отражение ...Геометрическая оптика
1.Основные положения геометрической оптики. Геометрическая оптика – это раздел оптики, изучающий законы распространения света в прозрачных средах ...Рздел физики: геометрическая оптика
Оптика представляет собой раздел физики, в котором изучаются явления и закономерности, связанные с возникновением, распространением и взаимодействием ...Волновая оптика в задачах повышенного уровня
Примерная программа среднего (полного) общего образования (базовый уровень). Электродинамика (35/5): волновые свойства света. Демонстрации: Интерференция ...Волоконна оптика
Що таке волоконна оптика? Волоконна оптика ― це область оптики, яка виникла у 50-их рр. XX ст. і займається вивченням властивостей і застосуванням ...Волновая оптика
Цель: повторение основных понятий, законов и формул ОПТИКИ в соответствии с кодификатором ЕГЭ. Элементы содержания, проверяемые на ЕГЭ 2010: Волновые ...Волновая оптика
В СЛОВЕ «СВЕТ» ЗАКЛЮЧЕНА ВСЯ ФИЗИКА С. И. ВАВИЛОВ. Объект исследования: Свет Предмет исследования: Волновые свойства света. Гипотеза: СВЕТ Волна Поток ...Конспекты
Оптика
ОУ: МОУ ОСШ №10, г. Усть-Кут. . Предмет: физика. . Повторительно–обобщающий урок в 9 классе по теме «Оптика». . Автор: Куркина Ольга Ивановна. ...Оптика
Урок физики. 11 класс. Тема:. Обобщение и закрепление знаний, умений и навыков по теме «Оптика». Цель урока: . Цель урока: повторение и закрепление ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 мая 2019
Категория:Физика
Содержит:30 слайд(ов)
Поделись с друзьями:
Скачать презентацию