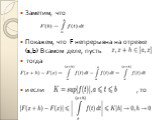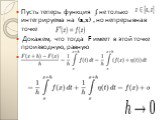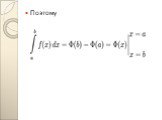Слайд 1Тема: Формула Ньютона-Лейбница
Работу выполнили: Павшинцев И.С. Чижков А.А.
Работу приняла: Плешакова О.В.
2010 год
Слайд 2план
1-Ньютон и Лейбниц 2- теорема 3- интеграл 4- применение интеграла 5-историческое значение и философский смысл формулы 6- список используемой литературы интернет ресурсы 7- конец!
Слайд 4Ньютон и Лейбниц
Из сохранившихся документов историки науки выяснили, что дифференциальное и интегральное исчисление Ньютон открыл ещё в 1665-1666 годы, однако не публиковал его до 1704 года.[70] Лейбниц разработал свой вариант анализа независимо (с 1675 года), хотя первоначальный толчок, вероятно, его мысль получила из слухов о том, что такое исчисление у Ньютона уже имеется, а также благодаря научным беседам в Англии и переписке с Ньютоном. В отличие от Ньютона, Лейбниц сразу опубликовал свою версию, и в дальнейшем, вместе с Якобом и Иоганном Бернулли, широко пропагандировал это эпохальное открытие по всей Европе. Большинство учёных на континенте не сомневались, что анализ открыл Лейбниц.
![Вняв уговорам друзей, взывавших к его патриотизму, Ньютон во 2-й книге своих «Начал» (1687) сообщил:[71] В письмах, которыми около десяти лет тому назад я обменивался с весьма искусным математиком г-ном Лейбницем, я ему сообщал, что обладаю методом для определения максимумов и минимумов, проведения Вняв уговорам друзей, взывавших к его патриотизму, Ньютон во 2-й книге своих «Начал» (1687) сообщил:[71] В письмах, которыми около десяти лет тому назад я обменивался с весьма искусным математиком г-ном Лейбницем, я ему сообщал, что обладаю методом для определения максимумов и минимумов, проведения](https://prezentacii.org/upload/cloud/15/01/11024/images/thumbs/screen5.jpg)
Слайд 5Вняв уговорам друзей, взывавших к его патриотизму, Ньютон во 2-й книге своих «Начал» (1687) сообщил:[71] В письмах, которыми около десяти лет тому назад я обменивался с весьма искусным математиком г-ном Лейбницем, я ему сообщал, что обладаю методом для определения максимумов и минимумов, проведения касательных и решения тому подобных вопросов, одинаково приложимых как для членов рациональных, так и для иррациональных, причем я метод скрыл, переставив буквы следующего предложения: «когда задано уравнение, содержащее любое число текущих количеств, найти флюксии[14] и обратно». Знаменитейший муж отвечал мне, что он также напал на такой метод и сообщил мне свой метод, который оказался едва отличающимся от моего, и то только терминами и начертанием формул.
![В 1693 году, когда Ньютон наконец опубликовал первое краткое изложение своей версии анализа, он обменялся с Лейбницем дружескими письмами. Ньютон сообщил:[72] Наш Валлис присоединил к своей «Алгебре», только что появившейся, некоторые из писем, которые я писал к тебе в своё время. При этом он потреб В 1693 году, когда Ньютон наконец опубликовал первое краткое изложение своей версии анализа, он обменялся с Лейбницем дружескими письмами. Ньютон сообщил:[72] Наш Валлис присоединил к своей «Алгебре», только что появившейся, некоторые из писем, которые я писал к тебе в своё время. При этом он потреб](https://prezentacii.org/upload/cloud/15/01/11024/images/thumbs/screen6.jpg)
Слайд 6В 1693 году, когда Ньютон наконец опубликовал первое краткое изложение своей версии анализа, он обменялся с Лейбницем дружескими письмами. Ньютон сообщил:[72] Наш Валлис присоединил к своей «Алгебре», только что появившейся, некоторые из писем, которые я писал к тебе в своё время. При этом он потребовал от меня, чтобы я изложил открыто тот метод, который я в то время скрыл от тебя переставлением букв; я сделал это коротко, насколько мог. Надеюсь, что я при этом не написал ничего, что было 6ы тебе неприятно, если же это случилось, то прошу сообщить, потому что друзья мне дороже математических открытий.

Слайд 7После появления первой подробной публикации ньютонова анализа (математическое приложение к «Оптике», 1704) в журнале Лейбница «Acta eruditorum» появилась анонимная рецензия с оскорбительными намёками в адрес Ньютона. Рецензия ясно указывала, что автором нового исчисления является Лейбниц. Сам Лейбниц решительно отрицал, что рецензия составлена им, но историки сумели найти черновик, написанный его почерком.[70] Ньютон проигнорировал статью Лейбница, но его ученики возмущённо ответили, после чего разгорелась общеевропейская приоритетная война, «наиболее постыдная склока во всей истории математики».[46]

Слайд 831 января 1713 года Королевское общество получило письмо от Лейбница, содержащее примирительную формулировку: он согласен, что Ньютон пришёл к анализу самостоятельно, «на общих принципах, подобных нашим». Рассерженный Ньютон потребовал создать международную комиссию для прояснения приоритета. Комиссии не понадобилось много времени: спустя полтора месяца, изучив переписку Ньютона с Ольденбургом и другие документы, она единогласно признала приоритет Ньютона, причём в формулировке, на этот раз оскорбительной в отношении Лейбница. Решение комиссии было напечатано в трудах Общества с приложением всех подтверждающих документов
![В ответ с лета 1713 года Европу наводнили анонимные брошюры, которые отстаивали приоритет Лейбница и утверждали, что «Ньютон присваивает себе честь, принадлежащую другому». Брошюры также обвиняли Ньютона в краже результатов Гука и Флемстида.[70] Друзья Ньютона, со своей стороны, обвинили в плагиате В ответ с лета 1713 года Европу наводнили анонимные брошюры, которые отстаивали приоритет Лейбница и утверждали, что «Ньютон присваивает себе честь, принадлежащую другому». Брошюры также обвиняли Ньютона в краже результатов Гука и Флемстида.[70] Друзья Ньютона, со своей стороны, обвинили в плагиате](https://prezentacii.org/upload/cloud/15/01/11024/images/thumbs/screen9.jpg)
Слайд 9В ответ с лета 1713 года Европу наводнили анонимные брошюры, которые отстаивали приоритет Лейбница и утверждали, что «Ньютон присваивает себе честь, принадлежащую другому». Брошюры также обвиняли Ньютона в краже результатов Гука и Флемстида.[70] Друзья Ньютона, со своей стороны, обвинили в плагиате самого Лейбница; по их версии, во время пребывания в Лондоне (1676) Лейбниц в Королевском обществе ознакомился с неопубликованными работами и письмами Ньютона, после чего изложенные там идеи Лейбниц опубликовал и выдал за свои.[73] Война не ослабевала до декабря 1716 года, когда аббат Конти сообщил Ньютону: «Лейбниц умер — диспут окончен
Слайд 10теорема
Теорема Если f непрерывна на отрезке a,b и Ф — ее любая первообразная на этом отрезке, то имеет место равенство
Слайд 11Доказательство
Пусть на отрезке (a,b) задана интегрируемая функция ʄ Начнем с того, что отметим, что то есть не имеет никакого значения, какая буква ( x или u ) стоит под знаком ʄ в определенном интеграле по отрезку (a,b)
Слайд 12Зададим произвольное значение x € (a.b) и определим новую функцию Она определена для всех значений x € (a.b) , потому что мы знаем, что если существует интеграл от ʄ на (a,b) , то существует также интеграл от ʄ на (a,b) , где Напомним, что мы считаем по определению
Слайд 13Заметим, что Покажем, что F непрерывна на отрезке (a,b) В самом деле, пусть тогда и если , то
Слайд 14Таким образом , F непрерывна на (a,b) независимо от того, имеет или не имеет ʄ разрывы; важно, что ʄ интегрируема на (a,b) На рисунке изображен график ʄ . Площадь переменной фигуры aABx равна F (X) Ее приращение F (X+h)-F(x) равно площади фигуры xBC(x+h) , которая в силу Ограниченности ʄ очевидно, стремится к нулю при h→ 0 независимо от того, будет ли x точкой непрерывности или разрыва ʄ например точкой x-d
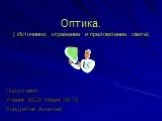
Слайд 15Пусть теперь функция ʄ не только интегрируема на (a,x) , но непрерывна в точке Докажем, что тогда F имеет в этой точке производную, равную В самом деле, для указанной точки x
Слайд 16Мы положили а так как ʄ (x) постоянная относительно t ,TO Далее, в силу непрерывности ʄ в точке x для всякого ε ˃0 можно указать такое δ что для Поэтому что доказывает, что левая часть этого неравенства есть о(1) при h→0
Слайд 17Переход к пределу в при h→0 показывает существование производной от F в точке и справедливость равенства . При x=a,b речь здесь идет соответственно о правой и левой производной. Если функция ʄ непрерывна на (a,b) , то на основании доказанного выше соответствующая ей функция имеет производную, равную Следовательно, функция F(x) есть первообразная для ʄ (a,b)
Слайд 18Мы доказали, что произвольная непрерывная на отрезке (a,b) функция ʄ имеет на этом отрезке первообразную, определенную равенством. Этим доказано существование первообразной для всякой непрерывной на отрезке функции. Пусть теперь есть произвольная первообразная функции ʄ(x) на (a,b) . Мы знаем, что Где C — некоторая постоянная. Полагая в этом равенстве x=a и учитывая, что F(a)=0 получим Ф(a)=C Таким образом, Но
Слайд 20Интеграл
Интеграл функции — естественный аналог суммы последовательности. Согласно основной теореме анализа, интегрирование — операция, обратная к дифференцированию. Процесс нахождения интеграла называется интегрированием. Существует несколько различных определений операции интегрирования, отличающиеся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат.
Слайд 21Типы интегралов
Определённый интеграл Неопределённый интеграл Интеграл Римана и Римана — Стилтьеса Интеграл Лебега и Лебега — Стилтьеса Интеграл Даниэля Кратный интеграл Криволинейный интеграл Поверхностный интеграл Эллиптический интеграл

Слайд 22История
Знаки интеграла ʃ дифференцирования dx были впервые использованы Лейбницем в конце XVII века. Символ интеграла образовался из буквы S — сокращения слова лат. summa (сумма). Интеграл в древности Интегрирование прослеживается ещё в древнем Египте, примерно в 1800 до н. э., Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды. Первым известным методом для расчёта интегралов является метод исчерпывания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известны. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны независимо в Китае в 3-м веке н.э Лю Хуэйем, который использовал их для нахождения площади круга. Этот метод был впоследствии использован Дзю Чонгши для нахождения объёма шара.

Слайд 23Историческое значение и философский смысл формулы Ньютона-Лейбница
Одним из важнейших исследовательских инструментов этого ряда является формула Ньютона-Лейбница, и стоящий за ней метод нахождения первообразной функции путем интегрирования ее производной. Историческое значение формулы в использовании бесконечно малых величин и абсолютно точном ответе на поставленный вопрос. Общеизвестны преимущества применения этого метода для решения математических, физических и прочих естественнонаучных задач, например, классической задачи о квадратуре круга – построении квадрата равновеликого заданному кругу. Философский смысл – в возможности получения информации о целом по его бесконечно малой части, замеченный ранее – наглядно реализуется в медицине и биологии, примером чему могут служить успехи генной инженерии в клонировании – создании взаимоподобных живых существ. Редким исключением в перечне наук, воспользовавшихся формулой Ньютона-Лейбница, остается история. Невозможность представления информации исторических источников в виде цифр – аргументов формулы – традиционна. Таким образом, до сих пор философский смысл формулы является не совсем философским, так как реализуется лишь в естественнонаучном знании, оставляя социально-гуманитарное знание без столь мощного инструмента. Хотя, если придерживаться традиционных особенностей социально-гуманитарного знания, его так сказать, слабостей, то и по делом ему.

Слайд 24Но дальнейший научный анализ дает в наше время новую, иную картину происходящего процесса. Ныне господствующие в науке атомистические воззрения разлагают материю на кучу мельчайших частиц или правильно расположенных центров сил, находящихся в вечных разнообразных движениях. Точно так же и проникающий материю эфир постоянно возбуждается и волнообразно колеблется. Все эти движения материи и эфира находятся в теснейшей и непрерывной связи с бесконечным для нас мировым пространством. Такое представление, недоступное нашему конкретному воображению, вытекает из данных физики .

Слайд 25Даже мистические и магические течения должны считаться с этим положением, хотя они могут, придав иной смысл понятию времени, совершенно уничтожить значение этого факта в общем миросозерцании. Таким образом, пока вопрос касается явлений, воспринимаемых органами чувств, даже эти наиболее далекие от точного знания области философии и религии должны считаться с научно доказанным фактом, как они должны считаться с тем, что дважды два – четыре в той области, которая подлежит ведению чувств и разума .

Слайд 26Вместе с тем объема накопленных человечеством знаний уже вполне достаточно для того, что бы эту традицию нарушить. В самом деле, нет необходимости на пифагорейский лад искать цифровое соответствие высказываниям «Петр I посетил Венецию во время Великого посольства» и «Петр I не был в Венеции во время Великого посольства», когда сами эти выражения легко могут служить аргументами алгебры логики Джорджа Буля . Результат каждого исторического исследования по сути и есть набор таких аргументов. Таким образом, оправдано, на мой взгляд, использование в качестве подинтегральной функции набора исторических исследований, представленных в виде аргументов алгебры логики, с целью соответствующего получения в качестве первообразной – наиболее вероятной реконструкции исследуемого исторического события. На этом пути есть много проблем. В частности: представление конкретного исторического исследования – производной реконструируемого события – в виде набора логических выражений – операция заведомо более сложная, чем, например, электронная каталогизация простого библиотечного архива. Однако информационный прорыв конца XX – начала XXI века (чрезвычайно высокая степень интегрированности элементной базы и увеличение мощности информационных ) делают выполнение такой задачи вполне реальным.

Слайд 27В свете вышесказанного, на современном этапе исторический анализ представляет собой математический анализ с теорией вероятности и алгеброй логики, а искомая первообразная функция – вероятность исторического события, что в целом вполне соответствует и даже дополняет представление о науке на современном этапе, ибо замена понятия сущность понятием функция – главное в понимании науки в Новое время – дополняется оценкой этой функции. Следовательно, современное историческое значение формулы в возможности претворения в жизнь мечты Лейбница «о том времени, когда два философа вместо бесконечных споров будут подобно двум математикам брать перья в руки и, засаживаясь за стол, заменять спор вычислением» . Каждое историческое исследование – заключение имеет право на существование, отражает реально происходившее событие и дополняет информационную историческую картину. Опасность вырождения исторической науки в набор бесцветных фраз-утверждений – результата применения предлагаемого метода, не больше опасности вырождения музыки в набор звуков, а живописи в набор красок на современном этапе развития человечества. Таким видится мне новый философский смысл формулы Ньютона-Лейбница, приведенной впервые в конце XVII – начале XVIII вв.

Слайд 28Собственно же формулу, ввиду особенности восприятия математических символов носителями социально-гуманитарного знания, выражающуюся в панической боязни этими носителями любого представления таковых знаков, приведем в словесной форме: определенный интеграл производной функции есть первообразная этой функции . Некоторое формальное отличие приводимого примера задачи о квадратуре круга от обычного учебно-математического примера вычисления площади, расположенной под произвольной кривой в декартовой системе координат, не меняет, естественно, сути.

Слайд 29ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА:
1. Бродский И.А. Сочинения в четырех томах. Т.3. СПб., 1994. 2. Вернадский В.И. Биосфера и ноосфера. М., 2003. 3. Вундт, Вильгельм. Введение в философию. М., 2001. 4. Гайденко П.П. Эволюция понятия науки. М., 1980. 5. Декарт, Рене. Размышления о первоначальной философии. СПб., 1995. 6. Карпов Г.М. Великое посольство Петра I. Калининград, 1998. 7. Кунцман П., Буркард Ф.-П., Видман Ф. Философия: dtv-Atlas. М., 2002. 8. Малаховский В.С. Избранные главы истории математики. Калининград, 2002. 9. Натансон И.П. Краткий курс высшей математики. СПб., 2001. 10. Энгельс Ф. Анти-Дюринг. М., 1988. 11. Шереметевский В.П. Очерки по истории математики. М., 2004 Интернет ресурсы http://ru.wikipedia.org


































![Ньютон и Лейбниц. Из сохранившихся документов историки науки выяснили, что дифференциальное и интегральное исчисление Ньютон открыл ещё в 1665-1666 годы, однако не публиковал его до 1704 года.[70] Лейбниц разработал свой вариант анализа независимо (с 1675 года), хотя первоначальный толчок, вероятно, Ньютон и Лейбниц. Из сохранившихся документов историки науки выяснили, что дифференциальное и интегральное исчисление Ньютон открыл ещё в 1665-1666 годы, однако не публиковал его до 1704 года.[70] Лейбниц разработал свой вариант анализа независимо (с 1675 года), хотя первоначальный толчок, вероятно,](https://prezentacii.org/upload/cloud/15/01/11024/images/thumbs/screen4.jpg)
![Вняв уговорам друзей, взывавших к его патриотизму, Ньютон во 2-й книге своих «Начал» (1687) сообщил:[71] В письмах, которыми около десяти лет тому назад я обменивался с весьма искусным математиком г-ном Лейбницем, я ему сообщал, что обладаю методом для определения максимумов и минимумов, проведения Вняв уговорам друзей, взывавших к его патриотизму, Ньютон во 2-й книге своих «Начал» (1687) сообщил:[71] В письмах, которыми около десяти лет тому назад я обменивался с весьма искусным математиком г-ном Лейбницем, я ему сообщал, что обладаю методом для определения максимумов и минимумов, проведения](https://prezentacii.org/upload/cloud/15/01/11024/images/thumbs/screen5.jpg)
![В 1693 году, когда Ньютон наконец опубликовал первое краткое изложение своей версии анализа, он обменялся с Лейбницем дружескими письмами. Ньютон сообщил:[72] Наш Валлис присоединил к своей «Алгебре», только что появившейся, некоторые из писем, которые я писал к тебе в своё время. При этом он потреб В 1693 году, когда Ньютон наконец опубликовал первое краткое изложение своей версии анализа, он обменялся с Лейбницем дружескими письмами. Ньютон сообщил:[72] Наш Валлис присоединил к своей «Алгебре», только что появившейся, некоторые из писем, которые я писал к тебе в своё время. При этом он потреб](https://prezentacii.org/upload/cloud/15/01/11024/images/thumbs/screen6.jpg)


![В ответ с лета 1713 года Европу наводнили анонимные брошюры, которые отстаивали приоритет Лейбница и утверждали, что «Ньютон присваивает себе честь, принадлежащую другому». Брошюры также обвиняли Ньютона в краже результатов Гука и Флемстида.[70] Друзья Ньютона, со своей стороны, обвинили в плагиате В ответ с лета 1713 года Европу наводнили анонимные брошюры, которые отстаивали приоритет Лейбница и утверждали, что «Ньютон присваивает себе честь, принадлежащую другому». Брошюры также обвиняли Ньютона в краже результатов Гука и Флемстида.[70] Друзья Ньютона, со своей стороны, обвинили в плагиате](https://prezentacii.org/upload/cloud/15/01/11024/images/thumbs/screen9.jpg)