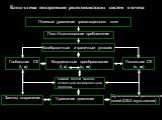
Презентация "Астрономические системы отсчета и методы их построения" по астрономии – проект, доклад
Презентацию на тему "Астрономические системы отсчета и методы их построения" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Астрономия. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
Планеты солнечной системы
Цель:. 1. Повторить - строение Солнечной системы; - чем звезды отличаются от планет; 2. Расширить знания о планете Земля. 3. Узнать, отчего зависит ...Характеристика планет солнечной системы
МЕРКУРИЙ МЕНЬШЕ ЗЕМЛИ В 3 РАЗА. МЕРКУРИЙ И ЗЕМЛЯ. Радиус планеты – 6052 км. Масса планеты – 0,815 массы Земли. Температура планеты – выше 470С Среднее ...Планеты солнечной системы
Вселенная. Вселенная – это все что существует. В нее входят все звезды, планеты и другие космические тела. Солнце. Cолнце - это обычная звезда, поверхность ...Солнце и планеты солнечной системы
ПЛАНЕТЫ СОЛНЕЧНОЙ СИСТЕМЫ. Со́лнце — центральная и единственная звезда нашей Солнечной системы, вокруг которой обращаются другие объекты этой системы: ...Строение солнечной системы
Тема урока: Строение солнечной системы. Вся Солнечная система – часть другой большой системы, которая называется галактикой. Так выглядит наша галактика ...Поиск жизни вне солнечной системы
Є багато чого на світі, друже Гораціо, що і не снилось нашим мудрецям . (Шекспір). ГЕОЦЕНТРИЧНА ТА ГЕЛІОЦЕНТРИЧНА. СИСТЕМИ СВІТУ. (Птолемей) (Коперник). ...Происхождение солнечной системы
Это наша галактика. С древних времен ученые хотели узнать, как она возникла. Наша солнеч- ная система. Фридрих Вильгельм (Уильям) Гершель ро дился ...Земля как планета солнечной системы
Что изучает наука астрономия. Астрономия - древнейшая из наук и самая молодая. Волнующие открытия достигаются сегодня с помощью самых сложных приемов ...Знакомство с малыми телами солнечной системы
Боде. Гершель. Пояс астероидов. Гаспра имеет неправильную форму. На фотографии «Галилео» видны кратеры вплоть до 160 м в поперечнике. Местоположение ...Звёзды и их строение
Звезды из вырожденного вещества. Коричневые карлики (T~700-2000K) Белые карлики (T~10000-100000K) Нейтронные звезды (T~0.1-0.3 кэВ). Средний импульс ...Земля – планета солнечной системы
Солнце – это звезда, пылающий газовый шар. ВРАЩЕНИЕ ЗЕМЛИ ВОКРУГ СОЛНЦА. ВОКРУГ СОБСТВЕННОЙОСИ. 365 ДНЕЙ 6 ЧАСОВ 9 МИНУТ. 24 ЧАСА. Декабрь Июнь Весна ...Другие звёздные системы- галактики
Цель работы: рассмотреть другие звездные системы, галактики и метагалактики. Рассмотреть: 1. Представление о галактиках 2. Понятие метагалктики 3. ...Движение планет солнечной системы
Движение планет Солнечной системы. Говоря о движении планет в Солнечной системе, хочется сказать, что практически все планеты, кометы и астероиды, ...Гипотезы происхождения солнечной системы
Что такое солнечная система? Солнце и все тела, обращающиеся вокруг него образуют СОЛНЕЧНУЮ СИСТЕМУ. Из чего состоит солнечная система? В состав солнечной ...Планеты солнечной системы
МЕРКУРИЙ. Ближайшая к Солнцу планета, по размерам похожая на Луну (радиус 2439 км), а по средней плотности (5.42 г/см3) на Землю. Ускорение свободного ...Знакомство с планетами солнечной системы
Содержание:. Солнечная система Планеты Как появились планеты Планеты Солнечной системы: Вывод. Меркурий Венера Земля Марс Юпитер Сатурн Уран Нептун. ...Планеты солнечной системы
Венера Земля Сатурн Юпитер Уран Плутон луна Марс Нептун Меркурий. Все планеты движутся вокруг Солнца по огромным кругам – орбитам. Меркурий немного ...Известные российские астрономы и их открытия
М.В. Ломоносов. Русский ученый-энциклопедист Михаил Васильевич Ломоносов оказал огромное влияние на развитие многих областей русской науки. Многое ...Происхождение солнечной системы
Содержание. Введение Строение Солнечной системы Представления о Земле, как о Центре Вселенной Становление гелиоцентрического мировоззрения Картины ...Изучение динамики солнечной системы
. План доклада. Состав и размеры Солнечной системы. Силы взаимодействия в Солнечной системе. Основные задачи динамики Солнечной системы. Методы наблюдений ...Конспекты
Определение расстояний до тел Солнечной системы и их размеров
Интегрированный урок (. физика + математика. ) в 12 классе. II. вида. Тема: «Определение расстояний до тел Солнечной системы и их размеров. ». ...Экспериментальные методы исследования частиц
Тема урока :. Экспериментальные методы исследования частиц. Цели урока :. Рассмотреть ионизирующее и фотохимическое действие частиц как основы ...Физические величины и их измерение
Урок 2. Физические величины и их измерение. . . Цели урока:. . а) образовательные. ученик должен усвоить:. - понятие физической величины ...Строение атома: планетарная модель и модель Бора. Квантовые постулаты Бора. Принцип действия и использование лазера. Экспериментальные методы регистрации заряженных частиц
Урок № 59-169 Строение атома: планетарная модель и модель Бора. Квантовые постулаты Бора. Принцип действия и использование лазера. Экспериментальные ...Самостоятельный разряд в газах. Различные типы самостоятельного разряда и их применение
Схема проведения урока. Физика 10 класс. Учитель физики. МОУ СОШ № 9. Ст. Расшеватской. Новоалександровского района. Ставропольского края. ...Различные состояния вещества и их объяснение на основе молекулярно-кинетических представлений
Приложение 1. Урок –. путешествие: «Сказка – ложь, да в ней намек». по теме: «Различные состояния вещества и их объяснение на основе молекулярно-кинетических ...Звезды и их классификация
Тема урока:. . Звезды и их классификация. . Цель урока:. . . познакомить учащихся с физическими характеристиками звезд, расширить мировоззрение ...Электромагниты, их свойства и применение
Электромагниты, их свойства и применение. Конспект деловой игры для 8 класса. Ц е л ь у р о к а: Продолжить развитие навыков самостоятельной работы ...Научные методы изучения природы.Физический эксперимент. Физическая теория
Предмет: Физика. . Класс: 7 рус. План занятия №. _. 5. __. Дата. 17. 09. 2013 год. Тема:. Научные методы изучения природы.Физический эксперимент. ...Материальная точка. Система отсчета
Кошикова Виктория Александровна. Учитель физики. МБОУ СОШ № 47 города Белгорода. «Материальная точка. Система отсчета». Цели урока:. . ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Астрономия
Автор презентации:доктор наук Копейкин С.М.
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию