Конспект урока «Испытания Бернулли» по математике

5. Домашнее задание: № 23.4, 23.5(в, г), 23.6(г) Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждение/ под ред. А.Г. Мордковича. – 2-е изд., доп. – М.: Мнемозина, 2008.

Тема урока 2. Формула Бернулли. Биноминальное распределение

Цели:

• ознакомление с применением формулы Бернулли при решении задач.

Задачи:

• формировать навыки решения задач по формуле Бернулли,

Ход урока

1. Организационный момент

2. Объяснение нового материала

Перейдем теперь к обещанным результатам, которые можно получить из свойств испытаний Бернулли.

Рассмотрим задачу: Пусть проводится серия из N испытаний. С какой вероятностью в этой серии произойдет ровно k успехов (т.е. событие А наступит ровно k раз)?

Пример 1. Три раза подряд бросаем симметричную монету. С какой вероятностью ровно k раз она выпадет на «орла»? Здесь речь идет о том, что в серии из трех испытаний Бернулли с произойдет ровно k успехов.

Решение: Обозначим интересующую нас вероятность идокажем следующую формулу Бернулли: .

Напомним, что через в комбинаторике обозначается число сочетаний, т.е. число способов, которым можно выбрать любые k из N предметов. Это число находится по формуле . Каждый исход такого «длинного» опыта закодируем последовательностью из букв У и Н, которые могут чередоваться в произвольном порядке.

Нетрудно сообразить, что в общем случае для N испытаний возможных исходов будет - это немедленно следует из правила умножения.

Будут ли все такие равновозможны? Разумеется, нет! Однако вероятность каждого исхода можно легко вычислить, пользуясь формулой произведения вероятностей для независимых событий. Поскольку все отдельные опыты в любой серии независимы, то вероятность любой последовательности из k успехов и (N - k) неудач может быть найдена по формуле .

Для доказательства формулы Бернулли остается сделать последний шаг – посчитаем, сколько всего серий, в которых содержится ровно k успехов.

У нас имеется N пустых мест, на которые нужно расставить k букв У и (N –k) букв Н. Сколькими способами это можно сделать? Каждый способ состоит в выборе тех k из N мест, на которых будут стоять буквы . Это можно сделать способами. Значит, всего таких серий будет , и вероятность интересующего нас события может быть получена как сумма вероятностей входящих в него исходов (все слагаемые в сумме одинаковые):

.

Формула Бернулли в самом общем случае доказана.

Вернемся к нашему примеру с троекратным бросанием монеты. Ответ на поставленный выше вопрос можно найти теперь по формуле Бернулли, применив ее для каждого значения k:

Поскольку в этом примере , то неудивительно, что симметричные значения вероятностей получились одинаковыми:

.

Рассмотрим пример, в котором вероятности успеха и неудачи разные.

Пример 2. Тестирование. Экзамен состоит из 16 вопросов. К каждому вопросу предлагается 4 варианта ответа, из которых ровно один верный. С какой вероятностью ученик, не знающий предмета, правильно ответит хотя бы на один вопрос?

Чтобы найти интересующую нас вероятность, перейдем к противоположному событию – ученик не ответит правильно ни на один из 16 вопросов. Эту вероятность можно найти по формуле Бернулли:

.

Отсюда, вероятность ответить хотя бы на один вопрос будет

.

Как видим, шансы хоть что-то угадать, даже при полном отсутствии знаний достаточно велики.

А теперь используя понятие случайной величины, можно дать равносильное определение схемы Бернулли. Пусть имеется последовательность независимых случайных величин , каждая из которых может принимать всего два значения 1 и 0 с вероятностями соответственно. Договоримся считать значение 1 – успехом, а значение 0 – неудачей. Тогда, как легко сообразить, число успехов в N испытаниях выражается случайной величиной , равной сумме величин : .

Используя полученную ранее формулу Бернулли, можно выписать закон распределения для случайной величины :

Значение

0	1	2	…	k	…	N
Вероятность

Это распределение называется распределением Бернулли.

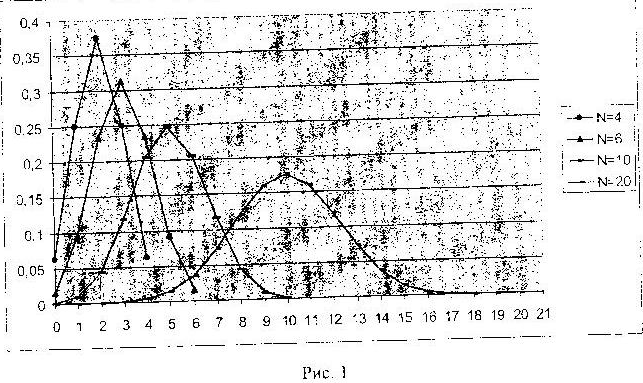
Как вы помните, для графического описания дискретного распределения используется полигон частот. Вот так будут выглядеть полигоны частот для биноминальных распределений с равными вероятностями и возрастающими значениями N:

А на рис. 2 изображены полигоны частот для биноминальных распределений с различными вероятностями успеха и неудачи – :

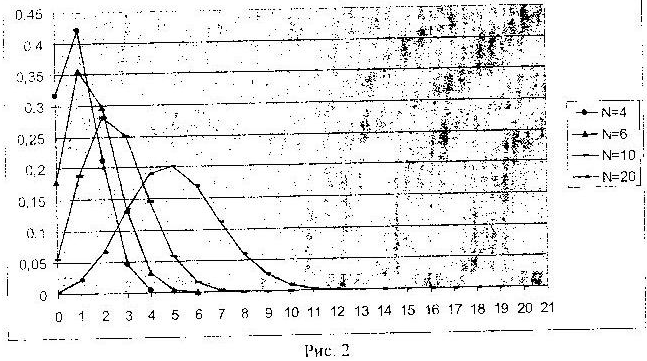
Из графика видно, что в симметричном случае максимум вероятности достигается ровно посередине, а для произвольного – в районе точки .

Более точно, справедлива теорема о наиболее вероятном числе успехов в схеме Бернулли: наиболее вероятным числом успехов в серии из N испытаний будет

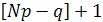• , если 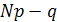не целое;

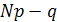• и 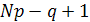, если 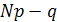целое.

3. Закрепление материала

Для закрепление разберем примеры.

Пример 1. Снова тестирование. Экзамен состоит из 16 вопросов. К каждому вопросу предлагается 4 варианта ответа, из которых ровно один верный. Положительная оценка ставится, если ученик ответил хотя бы на 5 вопросов. С какой вероятностью ученик, не знающий предмета, сдаст экзамен?

На этот раз нам придется применить формулу Бернулли несколько раз. Положительная оценка ставится за 5, 6,…, 16 правильных ответов. Поэтому искомая вероятность будет:

.

Мы ввели здесь специальное обозначение, которое будем использовать и в дальнейшем: .

Для вычисления суммы придется применить формулу Бернулли 12 раз. Можно сэкономить время, если решать задачу через дополнительное событие:

Как видите, вероятность, что ничего не знающий ученик сдаст экзамен, довольна велика.

Пример 2. При 100 бросаниях симметричной монеты наиболее вероятным числом «орлов» будет 50, а при бросании – 50 и 51.

Пример 3. При 16 вопросах в тесте и вероятности «угадывания» правильного ответа наиболее вероятным числом правильных ответов будет 4.

Пример 4. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.

Решение. Событие А – достали белый шар. Тогда вероятности
, .
По формуле Бернулли требуемая вероятность равна
.

Пример 5. Определить вероятность того, что в семье, имеющей 5 детей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.

Решение. Вероятность рождения девочки
, тогда .

Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:

, ,

, .

Следовательно, искомая вероятность

.

Пример 6. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.

Решение. Здесь опыт заключается в проверке каждой из 30 деталей на качество. Событие А - «появление нестандартной детали», его вероятность , тогда . Отсюда по формуле Бернулли находим
.

Пример 7. При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.

Решение. Вычисляем по формуле Бернулли:

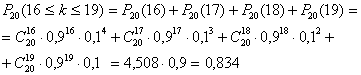
Пример 8. Независимые испытания продолжаются до тех пор, пока событие А не произойдет k раз. Найти вероятность того, что потребуется n испытаний (n ³ k), если в каждом из них .

Решение. Событие В – ровно n испытаний до k-го появления события А – есть произведение двух следующий событий:

D – в n-ом испытании А произошло;

С – в первых (n–1)-ом испытаниях А появилось (к-1) раз.

Теорема умножения и формула Бернулли дают требуемую вероятность:

Пример 9. Прививка от гриппа дает положительный результат в 70% случаев. Найти вероятность, что в группе из 15 человек более чем для двух она будет бесполезной.

Решение:

Согласно условию, вероятность того, что прививка даст положительный результат равна q=0,7. Найдем вероятность события А, состоящего в том, что в группе из 15 человек прививка будет бесполезной не более, чем для двух человек. Вероятность того, что прививка будет бесполезной, равна p=1-q=0.3.

Событие А равно сумме событий A0; A1; A2:
A0 - прививка будет полезна всем пациентам,
A1 - прививка будет бесполезна для 1 пациента,
A2 - прививка будет бесполезна для 2 человек.
Согласно формуле Бернулли, получим: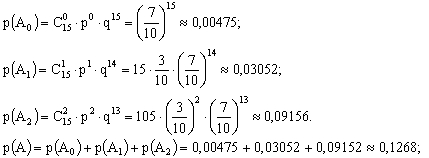

Тогда вероятность события , состоящего в том, что прививка будет бесполезна более чем для двух человек, равна:

4. Объяснение нового материала (продолжение)

Несложно посчитать числовые характеристики распределения Бернулли – математическое ожидание и дисперсию. Для этого можно воспользоваться тем, что случайная величина является суммой N независимых случайных величин: .

Используя свойства математического ожидания и дисперсии, получаем

и

.

Остается выяснить, чему равны математическое ожидание и дисперсия одной случайной величины . Заметим прежде всего, что они не зависят от i, поскольку все имеют одно и то же распределение:

Значение

0	1
Вероятность	q	p

Отсюда по определению математического ожидания и дисперсии получаем:

Подставляя найденные значения в формулы для , получаем:

5. Закрепление материала (продолжение)

Пример 1. Мишень установлена так, что может вращаться вокруг оси. При достаточно большой угловой скорости вращения стрелок не в состоянии различать цифры, выписанные по одной на секторах. Он вынужден стрелять наугад. При попадании в сектор 1 стрелок получает 1 р., в сектор 2 – 2 р., в сектор 3 – 3 р. и т.д., в сектор 8 – 8 р.. Стоит ли ему участвовать в такой игре, если за право стрелять один раз надо платить 5 р.?

Решение: Поскольку мишень вращается, то способности стрелка здесь не имеют никакого значения: попадание чистая случайность. Случайная величина х выражает возможные выигрыши. Она может принимать значения 1, 2, 3, 4, 5, 6, 7, 8. Так как все секторы одинаковые, то каждое из этих значений – случайная величина – принимает с одинаковой вероятностью . Значит,

Пример 2. В таблице дано распределение вероятностей случайной величины Z. Найдите математическое ожидание этой величины.

Значение

1	2	3	4	5	6
Вероятность

Решение:

Пример 3. Найдем ожидаемое среднее число удач при n = 20 испытаниях Бернулли с вероятностью успеха p = 0,4 в одном испытании.

Решение: .

Пример 4. В таблице дано распределение вероятностей некоторой случайной величины. Одна из вероятностей неизвестна. Найдите ее.

Значение

1	2	3	4	5	6
Вероятность				х

Решение: Так как сумма всех вероятностей равна 1, тогда

Ответ: .

6. Итоги урока

Вопросы и задачи:

1. Запишите формулу Бернулли.

2. Что такое распределения Бернулли? От каких параметров он зависит?

3. Чему равна сумма вероятностей всех возможных значений случайной величины?

4. Какова вероятность, что при бросании шести кубиков выпадет хотя бы одна шестерка?

5. Чему равно математическое ожидание и дисперсия случайной величины, распределенной по закону Бернулли (распределение Бернулли)

6. В подъезде горит 5 лампочек. Вероятность, что любая лампочка не сгорит в течение ближайшего месяца, равна 0,2. Какова вероятность, что в течение месяца:

а) сгорят все лампочки;

б) сгорит ровно одна лампочка;

в) останутся гореть по крайней мере 3 лампочки.

7. Вратарь футбольной команды отражает в среднем каждый третий пенальти. Сколько пенальти из пяти он отразит скорее всего? С какой вероятностью?

Формула Бернулли в сочетании с другими формулами теории вероятностей дает возможность вычислить вероятность сложных событий, возникающих в схеме Бернулли: вероятность того, что число успехов будет не больше (не меньше) заданного числа; что она будет лежать в заданном интервале и т.д. Для этого достаточно просуммировать вероятности соответствующих исходов, найденные по формуле Бернулли

7. Домашнее задание: № 23.19 (в, г), 23.20 (б, г), 23.17(в) Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждение/ под ред. А.Г. Мордковича. – 2-е изд., доп. – М.: Мнемозина, 2008.

Урок 3. Самостоятельная работа по теме «Испытание Бернулли».

Цель:

1. Развитие умения решать задачи с использованием формулы Бернулли;

2. Установить осознанность усвоения учащимися изученного материала по теме «Испытание Бернулли» и умения применять знания при выполнении практических заданий

Задачи:

• Контроль знаний, умений и навыков учащихся по теме «Испытание Бернулли»

Вариант I.

1. Подбрасываем монету 10 раз. Какова вероятность двукратного появления герба?

2. Вероятность того, что изделие не пройдет контроля, равна 0,125. Какова вероятность того, что среди 12 изделий не будет ни одного забракованного контролером?

3. Подводная лодка атакует крейсер, выпуская по нему одну за другой торпеды. Вероятность попадания каждой торпедой примерно равна 0,75. Любая из торпед с одинаковой вероятностью может пробить один из 10 отсеков крейсера, которые в результате попадания наполняются водой. При заполнении хотя бы двух отсеков крейсер тонет. Вычислите вероятность гибели крейсера.

4. При восьми бросаниях монеты орел может выпасть k = 0, 1, 2, 3, 4, 5, 6, 7, 8 раз. Составьте таблицу распределения вероятностей.

Вариант II.

1. Найти вероятность выбросить ровно 6 орлов, 10 раз бросив монету.

2. Вероятность заболевания гриппом во время эпидемии равна 0,4. Найдите вероятность того, что из 8 учеников класса заболеют 5 человек?

3. Вероятность попадания в мишень при выстреле равна 0,8. Найдите: а) вероятность того, что при семи выстрелах произойдет пять попаданий в мишень; б) наивероятнейшее число попаданий в мишень при семи выстрелах.

4. Стрелок не очень меток: Вероятность поражения мишени при одном выстреле оценивается в 40%. Составьте таблицу распределения вероятностей, если число попаданий k = 0, 1, 2, 3, 4, 5.

Решение:

Вариант I.

1. В этом случае n = 10, k = 2, p = , q = , тогда

Ответ: 0,044.

2. Имеем n = 12, k = 0, p = 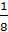, q = 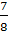. По формуле Бернулли имеем

Ответ: 0,2514.

3. Обозначим события:

А₁ – «попадание одной торпедой»

А₂ – «попадание двумя торпедами»

А₃ – «попадание тремя торпедами»

А₄ – «попадание четырьмя торпедами»,

А – «крейсер потоплен»

Тогда

По формуле полной вероятности

Ответ: 0,92

4. Используя полученную формулу Бернулли, выпишем закон распределения для случайной величины :

Значение

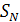0	1	2	…	k	…	N
Вероятность

Подставляя в формулу значения n = 8,

Значение

0	1	2	3	4	5	6	7	8
Вероятность	0,004	0,031	0,109	0,219	0,273	0,219	0,109	0,031	0,004

Вариант II.

1. В этом случае n = 10, k = 6, p = , q = , тогда

Ответ: 0,2051.

2. Рассматриваемый в задаче сюжет удовлетворяет схеме Бернулли, где n = 8, k = 5, p = 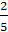, q = 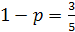. Поэтому по формуле Бернулли имеем

Ответ: 0,1239.

3. Рассматриваемый в задаче эксперимент удовлетворяет схеме Бернулли.

Пусть А – событие «Попадание в мишень при выстреле». Тогда событие означает «промах». По условию , значит .

а) Для нахождения пяти попаданий при семи выстрелах воспользуемся формулой Бернулли: .

б) Наивероятнейшее число попаданий в мишень при семи выстрелах находим из двойного неравенства , т.е. . Значит,

Ответ: а) 0,275; б) 6.

4. Используя полученную формулу Бернулли, выпишем закон распределения для случайной величины :

Значение

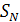0	1	2	…	k	…	N
Вероятность

Подставляя в формулу значения n = 5,

Значение

0	1	2	3	4	5
Вероятность	0,078	0,259	0,346	0,23	0,077	0,01

Список использованной литературы:

1. Е.А. Бунимович, В.А. Булычев. Вероятность и статистика в курсе математики общеобразовательной школы: лекции 5 – 8. – М.: Педагогический университет «Первое сентября», 2006.

2. Вероятность и статистика. 5 – 9 кл.: пособие для общеобразоват. учреждений/ Е.А. Бунимович, В.А. Булычев. – 5-е изд., стереотип. – М.: Дрофа, 2007.

3. Лютикас В.С. Факультативный курс по математике: Теория вероятностей: Учеб. пособие для 9 – 11 кл. сред. шк. – 3-е изд., перераб. – М.: Просвещение, 1990.

4. Тонких А.П. Математика: Учебное пособие для студентов факультетов подготовки учителей начальных классов: В 2-х книгах. Кн. 1. – М.: Книжный дом «Университет», 2002.

5. Теория вероятностей и статистика/ Ю.Н. Тюрин, А.А. Макаров, И.Р. Высоцкий, И.В. Ященко. – 2-е изд., переработанное. – М.: МЦНМО: ОАО «Московские учебники», 2008.

Задачи для контрольной работы

1. Бросили игральную кость. Успехом будем считать выпадение шестерки. Неудачей – выпадение иного числа очков. Таким образом, 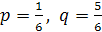. Найдите вероятность того, что бросив кость 8 раз, мы выбросим шестерку не менее 4, но не более 6 раз.

Решение: Отдельно найдем вероятности того, что шестерка выпала 4, 5 или 6 раз, и их сложить:

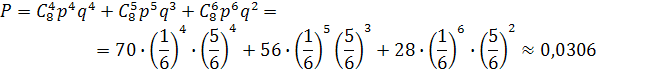
Ответ: 0,0306.

2. Найдем вероятность события А, состоящего в том, что в серии из 6 испытаний Бернулли с вероятностью успеха p = 0,3 наступит хотя бы один успех.

Решение: Вместо события А рассмотрим противоположное событие - «наступит 0 успехов». Вероятность этого события найти несложно. Учитывая, что вероятность неудачи q равна 0,7, получаем

.

Следовательно,

Ответ: 0,882351