Конспект урока «Треугольник» по геометрии для 5 класса

Автор: Малкова Надежда Геннадьевна,

учитель математики МБОУ Лицей № 40 г.Нижний Новгород

Класс: 5

Тема: Треугольник

Тип урока: Объяснение нового материала

Форма работы: групповая

Методы обучения: словесные и наглядные

Инструменты: карандаши, линейки, чистые листы бумаги, модели треугольников, ножницы, цветная бумага, модели тетраэдра, октаэдра, икосаэдра.

При проведении урока «Треугольник» ( 5 класс) используется групповая и парная работы.

Предлагаемые упражнения и работа с моделями многогранников подобраны так, чтобы ученики могли анализировать новые для них ситуации

Словесный и наглядный методы обучения позволяют воспринимать материал в удобной для ученика форме.

Доступность обеспечивается постепенным «вхождением в ситуацию»: творческие работы, эксперименты с геометрическими фигурами. Дифференцированный подход проявляется при групповой самостоятельной работе. Ученик «берет» то, что по его силам и знаниям на данный момент.

Данный урок первый по теме «Треугольник». Практическая направленность учебного материала имеет, на мой взгляд, большое значение для формирования творческих способностей пятиклассника.

Урок в 5-м классе по теме: "Треугольник".

Ход урока.

1.Оргмомент.

Цель: включение в деловой ритм настрой на урок

Учитель: Положите свою ладошку на лист, лежащий перед вами. Обведите ладошку. Посмотрите на ладошку соседа. Ладошки получились разные. Почему они разные? Мы сами разные. Мыслим по-разному. Отвечаем по-разному. Но мы учимся понимать друг друга. Напишите на ладошке себе пожелание, как вы будете работать, отвечать, помогать другу, помогать соседу по парте. В конце урока проверим, смогли ли вы спрогнозировать свой успех .Одно важное условие: пишем кратко.

2.Постановка познавательной задачи.

Цель: организация учащихся по принятию познавательной задачи.

Учитель: Бермудский треугольник — легендарная область Атлантического океана между Пуэрто-Рико, Флоридой и Бермудскими островами, в которой, согласно мнению многих исследователей, происходит множество необъяснимых явлений. О нем много написано и даже сняты фильмы. В чем же его загадочность? (Заслушать ответы). Действительно, загадочность его заключается в том, что в нём бесследно исчезали корабли и самолёты. Природа “бермудского треугольника” тревожит ученых по сей день. (Приложение 1. Для интересующихся учащихся).Однако английский исследователь Лоуренс Д. Куше собрал и проанализировал в хронологическом порядке более 50 случаев исчезновения судов и самолетов в этом районе и пришел к выводу, что легенда о «треугольнике» — не более чем искусственно сфабрикованная мистификация, которая явилась результатом небрежно проведенных исследований, а затем была доработана авторами, увлекающимися сенсациями. Этой же точки зрения придерживался советский академик Л.М. Бреховских и многие другие исследователи.

Учитель: Во время моего небольшого рассказа прозвучало название фигуры, вам, известное. Так, какой геометрической фигуре посвятим наш урок? Треугольнику.(слайд 1,2)

Учитель: Тема нашего урока “Треугольник”. (Запись на доске).

-У вас на столах таблица, которую нужно заполнить ( работа в парах):

Знаю

Заслушать результаты работы. Таблица заполняется вся, т.к. в начальной школе ученики уже знакомились с треугольником.

Учитель: А теперь составим кластер по теме «Треугольник».

- Как будем работать? Индивидуально, в парах, в группах? Ученики выбирают групповую форму работы. (В данном случае в группе нужны взаимообмен мнениями, обсуждение разных аспектов проблемы, поиск неодинаковых или многоплановых решений, поэтому в нее включают школьников с разными подструктурами мышления). Группы составляют вопросы для кластера. Кластеры в группах получаются разными.

- Что получилось? (Представлен кластер, составленный учениками одной из групп).

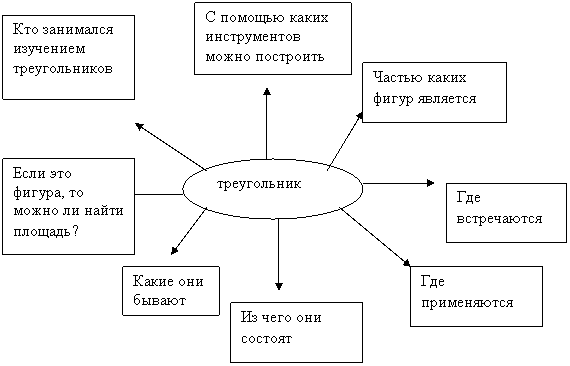
3.Усвоение новых знаний.

Цель: ввести понятие треугольника, его элементов, обозначение; ознакомить учащихся со свойствами треугольника; побуждать детей “добывать” новые знания.

- Рассматривается кластер. Сравниваем с кластером учителя (заранее заготовленный на листах, раздается в каждую группу). Слайд 3.

Учитель: С какого вопроса начнем изучение темы? (Обсуждение в группе).

Выясняем, что вопрос «что такое треугольник» в кластере учеников не выделен. Заостряем вопрос на том, «какая фигура называется треугольником».

Учитель: В каждой группе имеются чистые листы. В течение урока мы будем их заполнять. Итак, начнем работу. Выполните работу: в рабочих листах нужно отметить три точки, обозначить их прописными латинскими буквами А, В и С. Соединить точки попарно ( по две) отрезками. Результат работы предъявите на больших листах.

В процессе работы выясняем, что не все группы рассмотрели два случая :

1) три точки лежащие на одной прямой

2) три точки не лежащие на одной прямой.

Обсуждаем, почему так получилось. Уточняем:

- Если точки лежат на одной прямой и эти точки соединены отрезками попарно, то какую фигуру мы получили? (треугольник “выродился” в отрезок).

-Если точки не лежат на одной прямой и эти точки соединены попарно отрезками, то какую фигуру мы получили? ( получился Δ АВС).

Оба случая нужно изобразить в тетради (слайд 4).

Учитель: Так что такое треугольник? (Учащиеся заполняют пропуски в определении треугольника в рабочих листах, заслушивается ответ от группы) .

Лист. Определение треугольника.

Треугольник – это геометрическая фигура, состоящая из _____ точек, не лежащих на одной прямой и ______ отрезков, соединяющих эти точки.

Сравниваются определения свои и то, что получили.

Треугольник – это геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой, и трёх соединяющих их отрезков.

- Вместо слова “треугольник” употребляют знак . Запишем Δ АВС.

Учитель: Ребята, как называются три точки А, В и С в Δ АВС? Как называются отрезки, соединяющие эти точки? (идет обсуждение). Какие элементы есть еще у треугольника? Сколько их ? (Выясняем в группах, обсуждаем, записываем).

Учитель: Изобразите треугольник МNK. Назовите элементы треугольника МNK (обсуждение в группах, заслушиваем ответы), записываем информацию (слайд 5)

вершины:______________

стороны:_______________

углы:__________________

-Дан треугольник КРС. Назовите элементы треугольника КРС, не используя чертеж. Выясняем, как нужно работать, чтобы легко определить стороны, вершины, углы (группы обсуждают, заслушать версии), подвести итог(работа со слайдом 5)

вершины – перечисляем буквы в названии треугольника К, Р, С

углы – добавляем к каждой букве слово «угол»: угол К, угол Р, угол С

стороны –чертим стрелку от Р к К (проговариваем сторона РК), чертим стрелку от Р к С (проговариваем сторона РС), чертим стрелку от С к К (проговариваем сторона КС). Изобразить на доске и показать на слайде.

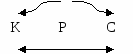
РК РС

КС

А теперь рассмотрим свойства треугольника

Учитель: У меня в руках четырёхугольник. Не меняя длины сторон, могу я изменить форму?

- заслушать ответы.

Учитель: Попробуйте.( Работа с моделями). А если взять треугольник? (Работа в группах. Ребята выясняют, можно ли изменить форму треугольника. Работа с моделями). Сделайте вывод. Выводы заслушиваются от каждой группы. Потом делаем общий вывод.

-  Вывод (после обсуждения): Треугольник – “жесткая” фигура. Если заданы три его стороны, то форму треугольника уже изменить нельзя, не разрушив его. Это свойство широко используется на практике.

Учитель: Приведите примеры. Обсуждение в группах. Ученики приводят примеры.

-Вывод: Чем больше треугольников в любой конструкции, тем она прочнее.

Учитель: Как вы думаете, чему равна сумма углов любого треугольника? (Заслушать ответы от каждой группы. Записать гипотезы на доске.). Верны ли ваши предположения? Данный вопрос предлагаю рассмотреть дома.

Учитель: Продолжим знакомство с треугольником.

-У треугольника есть пространственные родственники (демонстрация моделей). Модели есть в группах. (слайд 6)

1) тетраэдр,

2) октаэдр,

3) икосаэдр.

А почему эти геометрические тела являются родственниками треугольника?(Ученики рассматривают модели, обсуждают вопрос в группах. Делают вывод. Выводы заслушиваются)

-Ученики: Грани этих тел – треугольники.

Учитель: Давайте с вами сконструируем геометрическую бумажную игрушку, которая тоже является родственником треугольника, так как её поверхность состоит из треугольников. Эта игрушка называется флексагон . Она удивительна тем, что внезапно изменяет свою форму и цвет. Одна сторона красная, другая жёлтая. Превратим его в зеленый флексагон.

Совместная работа в группе помогает быстро всем освоить построение флексагона. Ученики помогают друг другу в построении игрушки.

Учитель: Игрушка вам понравилась? Пусть флексагон останется доброй памятью о нашем уроке, который был посвящен треугольнику.

4. Домашнее задание. (Дифференцировано)

Учитель: А теперь задание на дом (группы выбирают задания).

Выполните рисунок с изображением применения “жесткости” треугольника в быту.

По желанию сочинить небольшое стихотворение о треугольнике или флексагоне.

Выбрать вопрос из кластера и подготовить к следующему уроку.

Исследовать вопрос об измерении углов треугольника.

Итог.

Учитель: У вас на столах заполненная маркировочная таблица. Смотрим записи в столбиках. Работаем с последним столбиком. Если существует необходимость дополнения записей в столбике, то они выполняются. Если в процессе работы уточнения были ликвидированы, то их вычеркиваем. Оставляем только те записи, которые требуют уточнения.

  Знаю

 Маркировочная таблица дает возможность выявить затруднения ученика. Учитель, имея полную картину затруднений, строит следующий урок с опорой на графу «необходимо уточнить»

Учитель: Вернемся к ладошке, которую рисовали в начале урока. Посмотрите на то, что вы на ней написали. Совпали ли ваши пожелания с тем, что вы получили в конце урока. (Выясняем, что не у всех ребят полное совпадение написанного с полученным. Выясняем, почему так получилось.)

5. Невозможные треугольники (на столах в группах лежат рисунки треугольника Пенроуза. Приложение 2.)

- Плоский рисунок может обманывать, изображая невозможное. Я предлагаю рассмотреть невозможный пространственный объект - треугольник Пенроуза. Закройте одну из вершин этого треугольника, и станет ясно, что одна из его сторон направлена к нам, а другая – от нас, т. е. они не могут соединиться в пространстве. (Смотрите приложение ) (слайд 7,8)

ПРИЛОЖЕНИЕ 1

ВСЕ О БЕРМУДСКОМ ТРЕУГОЛЬНИКЕ

1. Эти необъяснимые "Бермуды"
   
   Понятное дело, катастрофы в этом районе происходили и раньше, как и в других треугольниках, овалах и квадратах, которые можно вообразить на глобусе. Но в знаменитом Бермудском треугольнике они происходили значительно чаще, и самое главное – при удивительных обстоятельствах. Все они были собраны в книге, написанной Ч. Берлицем, которого можно считать основоположником мифа. Самый важный вывод, который сделал Белиц, – это утверждение, что катастрофы с самолетами и судами в этом районе невозможно объяснить естественными причинами.
   
   Свою печальную известность Бермудский треугольник приобрел еще в 1840 году, когда недалеко от порта Нассау — столицы Багамских островов — было обнаружено французское парусное судно «Розали», находившееся в дрейфе. На нем были подняты все паруса, имелась вся необходимая оснастка, но сама команда корабля отсутствовала. Это показалось очень странным. После осмотра было установлено, что судно находится в прекрасном состоянии, не имеет никаких повреждений, груз его цел. Но куда исчез экипаж?

2. Многие из исследователей предлагают продолжить бермудский треугольник на восток в Атлантический океан вплоть до Азорских островов, отдельные черезчур рьяные головы отодвинул бы его границу еще дальше к северу. Следовательно бермудский треугольник не является строго ограниченной географической областью, как, скажем Бенгальский залив или Берингово море. Не является он и узаконенным географическим названием. Поэтому и пишется со строчной буквы. Если же мы будем настаивать на классическом треугольнике, ограниченном тремя указанными вершинами, то в конце концов убедимся , что почти половина всех таинственных исчезновений, которыми так богата прославился треугольник, в него не войдет. Некоторые из этих случаев произошли далеко на востоке в Антлантике, другие, наоборот, в полосе между треугольником и побережьем США, третьи – в Мексиканском заливе или в Карибском море.

3. Площадь Бермудского треугольника – в границах между Бермудскими островами, Майами во Флориде и Пуэрто-Рико – составляет свыше одного миллиона квадратных километров. Этот район мало отличается от других похожих мест на Земле. И, тем не менее, именно в районе Бермудского треугольника загадочно исчезали суда, а затем и самолеты. Во всяком случае, многие об этом говорят и многие в это верят.

Гипотеза
Версию о том, что причиной бесследного исчезновения морских судов и самолетов в Бермудском треугольнике являются кристаллогидраты метана, выдвигал еще в 1988 году британский геолог Бен Кленнел. Под влиянием идущего из земных недр тепла и других факторов метан выделяется из кристаллогидратов и образует огромные пузыри под донными осадками. Такие пузыри могут под действием незначительных усилий – даже, например, потревоженные китом, – вырываться на поверхность моря. Такие пузыри просто переворачивают корабли, а затем затягиваются в образовавшуюся водяную воронку. Ну а вырвавшийся на поверхность газ может взрываться при соприкосновении с воздухом, от чего гибнут и самолеты. Австралийцы Джосеф Монаган и Дэвид Мей провели опыты на моделях кораблей в бассейне, а также серию экспериментов с компьютерным моделированием, и показали, что вероятность действия такого механизма даже выше, чем предполагал Бен Кленнел. Таким образом, такое выделение метана из кристаллогидратов, а затем его возгорание не исключает подобных катастроф и в будущем. Особую опасность в этом отношении представляет потепление, которое может стимулироваться техногенными выбросами углекислого газа в атмосферу. Нарушение природного равновесия в результате технологической деятельности людей способно разбудить и привести в действие механизм выделения метана из кристаллогидратов океанов со всеми вытекающими отсюда последствиями.

ПРИЛОЖЕНИЕ 2

ТРЕУГОЛЬНИК ПЕНРОУЗА

ЛИТЕРАТУРА: 

Окунев А.А.Спасибо за урок, дети! // М:-Просвещение-1988

Смирнова Е.С .Методическая разработка курса наглядной геометрии: 5 класс.// Книга для учителя.-М:-Просвещение,1999

Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия.5-6 кл. //Учебное пособие.-М.:-Дрофа- 1998.

Сайты:

«Невозможные фигуры в реальном мире», Дж.Тимоти Анрах «Удивительные фигуры», http://im-possible.info