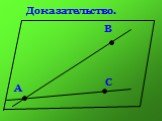
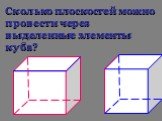
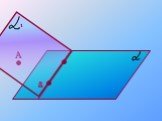
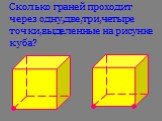
Презентация "Следствия из аксиом стереометрии" по математике – проект, доклад
Презентацию на тему "Следствия из аксиом стереометрии" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 42 слайд(ов).
Слайды презентации
Список похожих презентаций
Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...Аксиомы стереометрии и их простейшие следствия
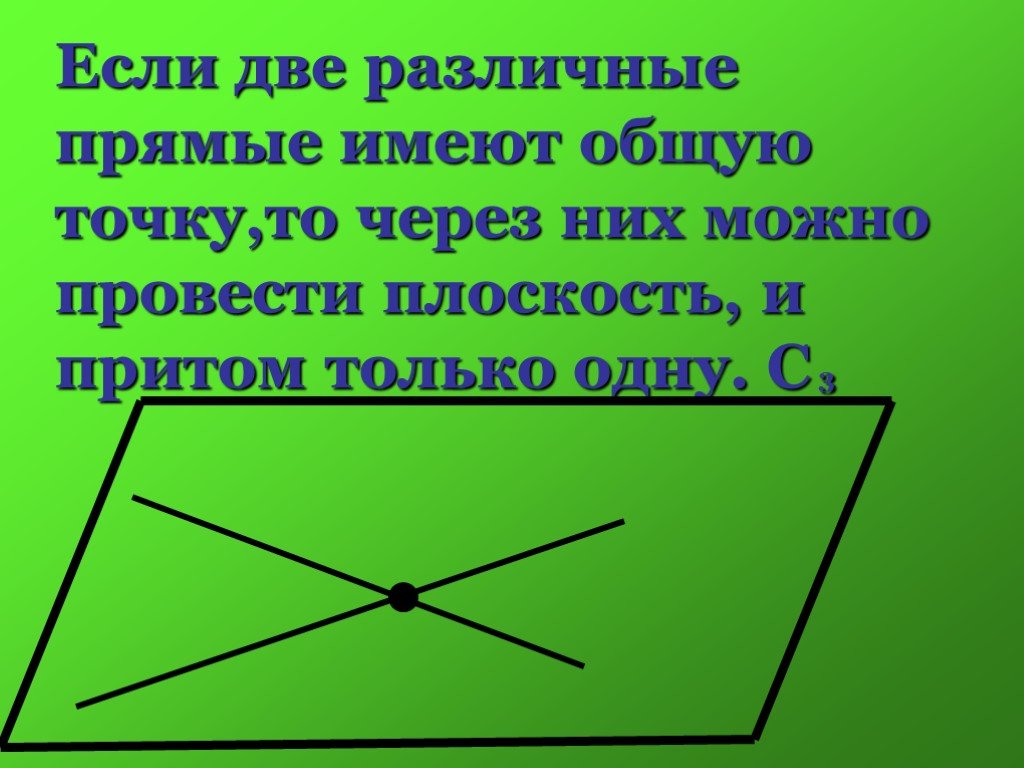
Аксиомы стереометрии. 1)Какова бы ни была плоскость, существуют точки, принадлежащие ей и точки, не принадлежащие ей. 2) Если две плоскости имеют ...Аксиомы стереометрии и их следствия
Цели:. Изучить аксиомы стереометрии: - о взаимном расположении точек, - о взаимном расположении прямых, - о взаимном расположении плоскостей в пространстве. ...Аксиомы стереометрии
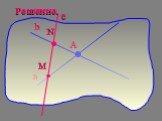
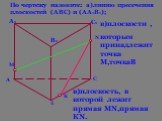
Аксиомы стереометрии. Сформулируйте содержание аксиом А1, А2, А3, А4 Прокомментируйте их с помощью приведенных ниже рисунков. α С В А. Через любые ...Аксиомы стереометрии
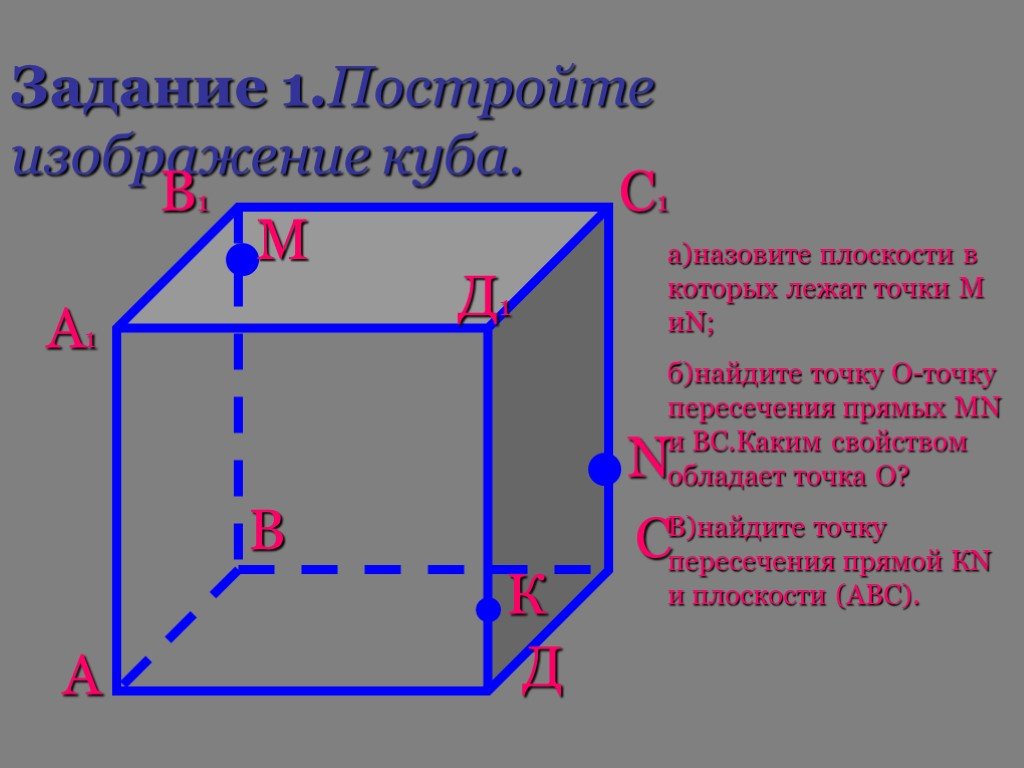
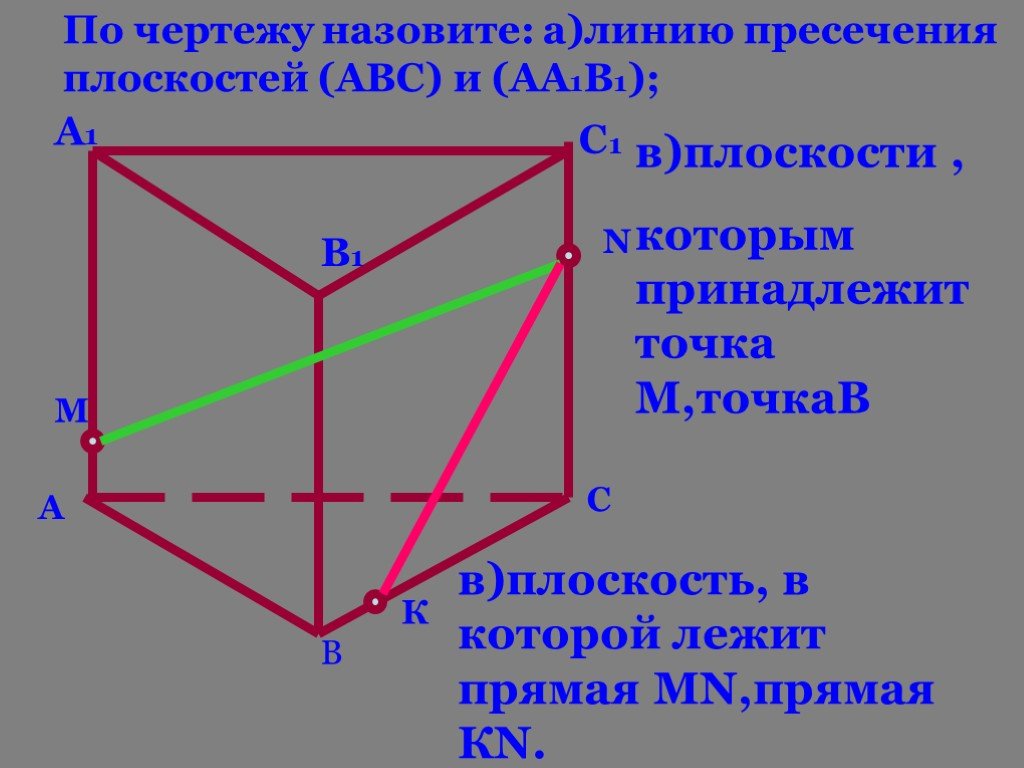
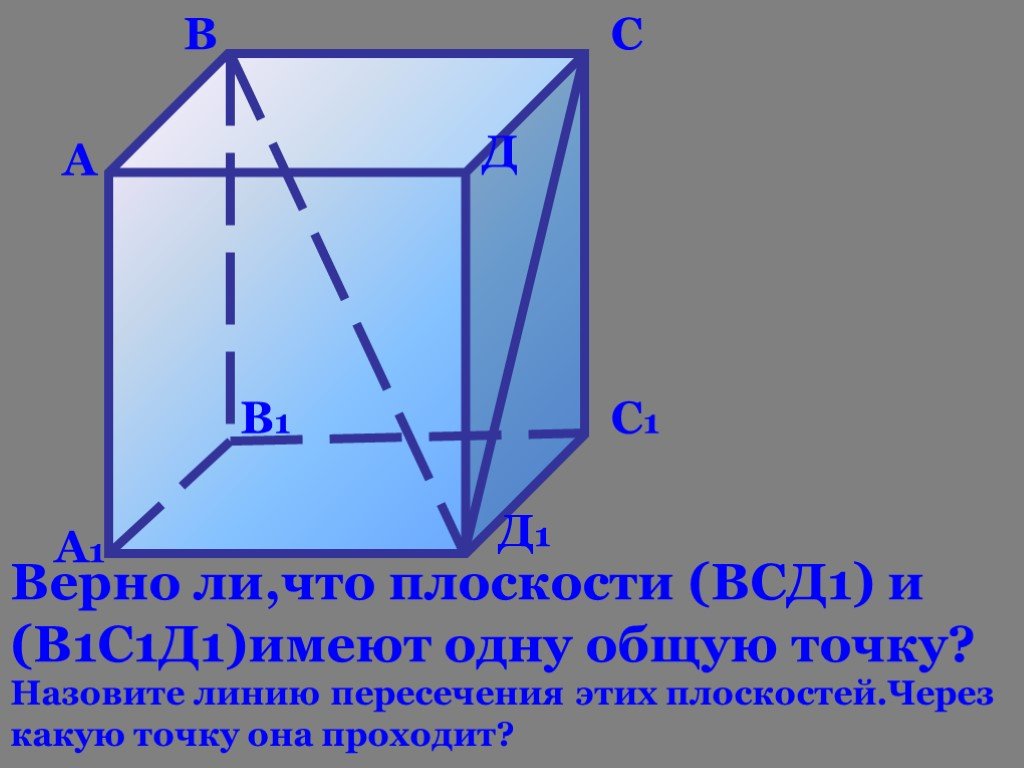
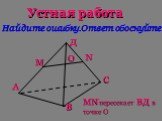
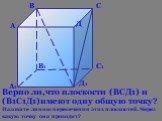
1 3 4 5 А1 А3 С1. Дан куб АВСDA1B1C1D1. D1 D С В1 В А M. Точка М лежит на ребре DD1. N. Точка N лежит на ребре CC1. K. Точка K лежит на ребре BB1. ...Аксиомы стереометрии
ОСНОВНЫЕ ПОНЯТИЯ. Расстояние, точка, прямая, плоскость, Множество. обозначения плоскостей. М – все точки пространства. Аксиома 1. В пространстве существуют ...Аксиомы стереометрии Решение задач
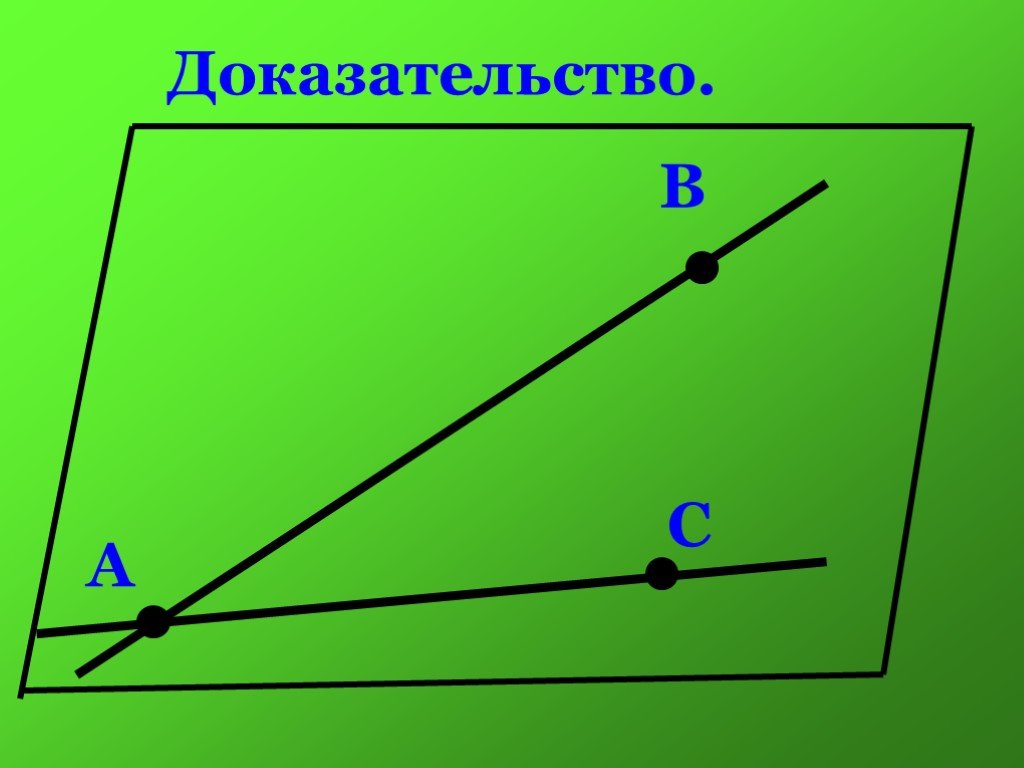
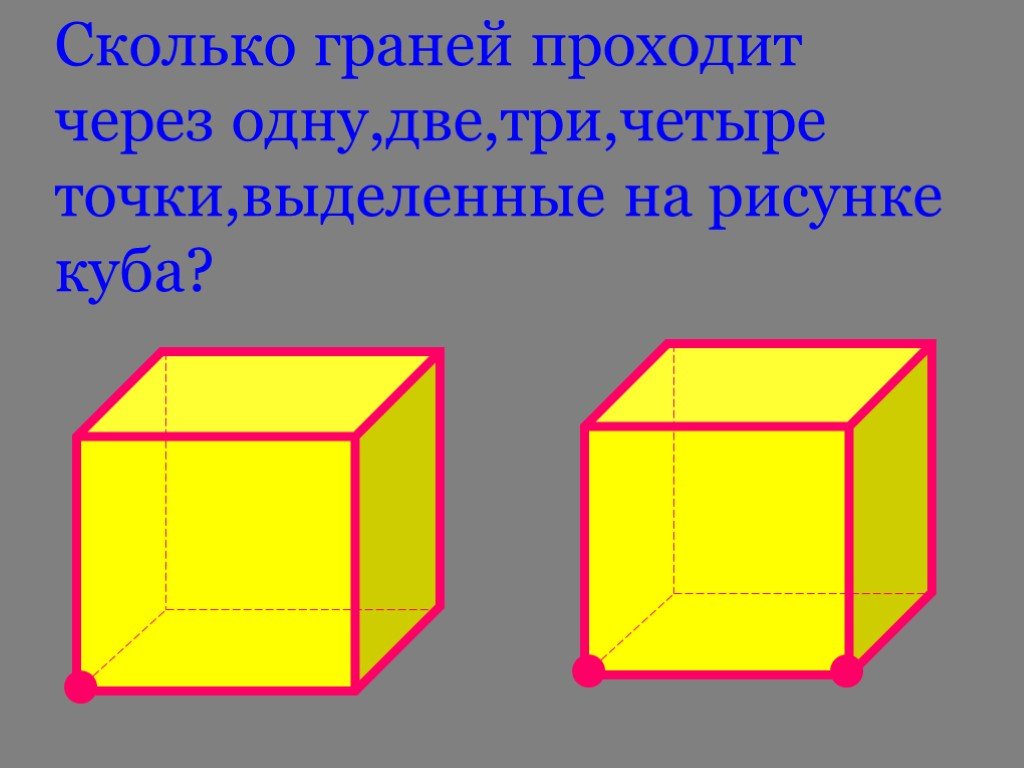
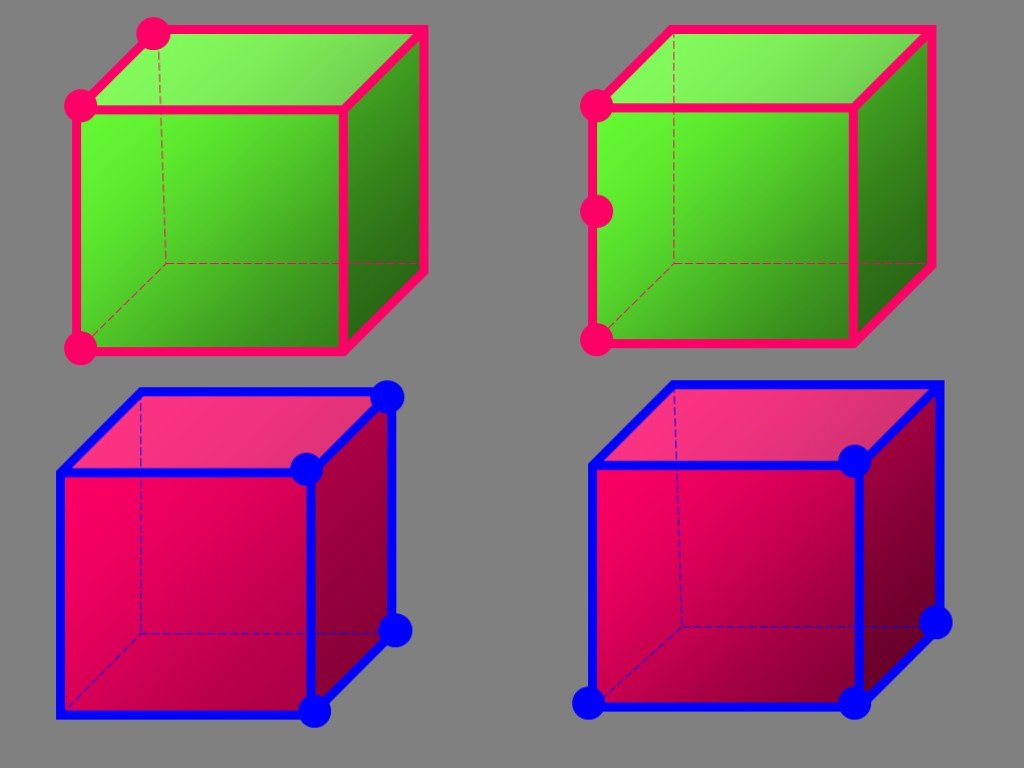
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...Аксиомы стереометрии
Повторить аксиомы планиметрии Познакомиться с аксиомами стереометрии Уметь соотносить математическую формулировку аксиомы с графическим изображением ...Аксиомы стереометрии
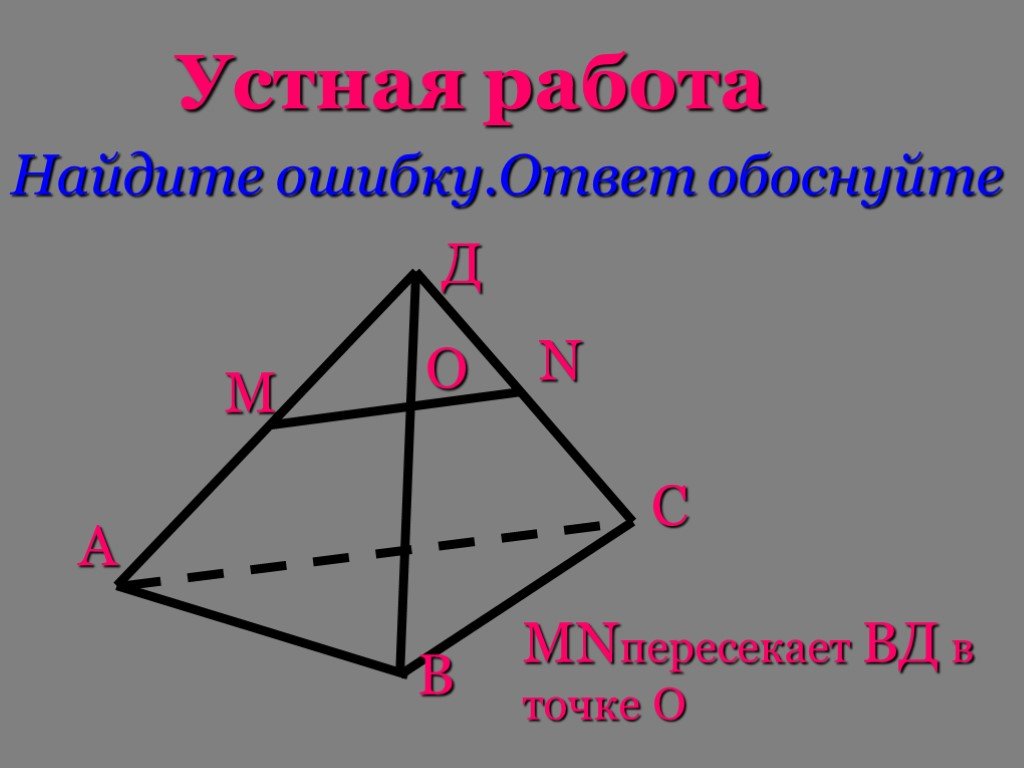
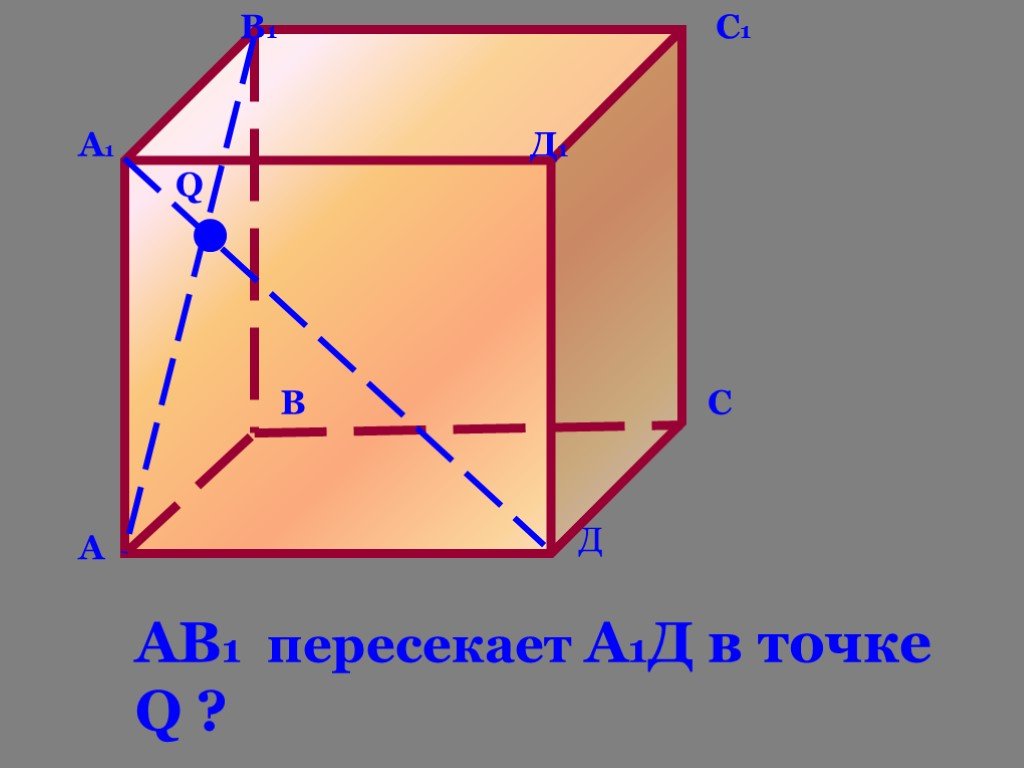
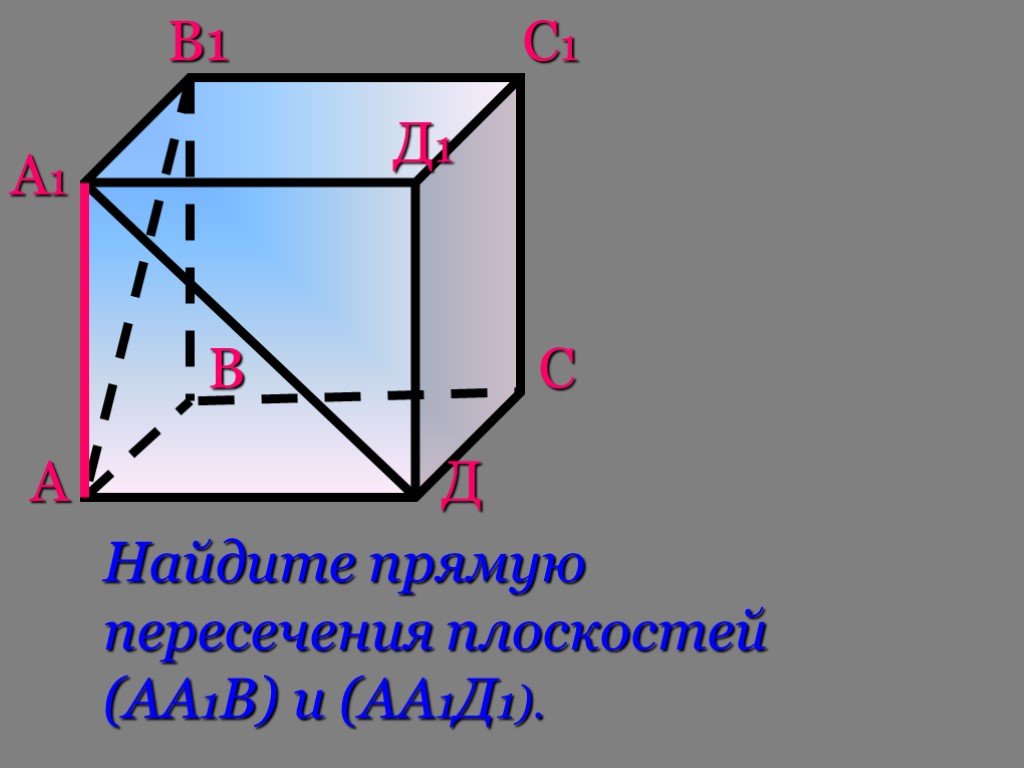
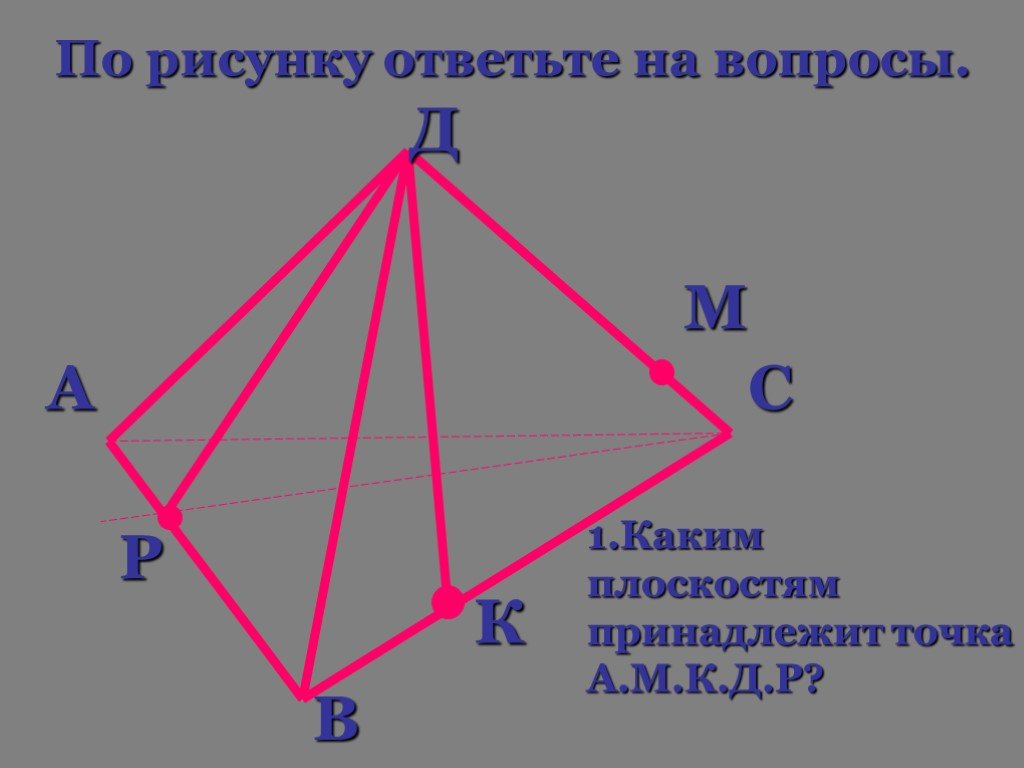
Содержание:. 1.Понятия стереометрии 2. Изображение плоскости 3.Аксиомы стереометрии 4.Следствия из аксиом стереометрии. Система аксиом стереометрии ...Изучение сечений в стереометрии с помощью компьютера
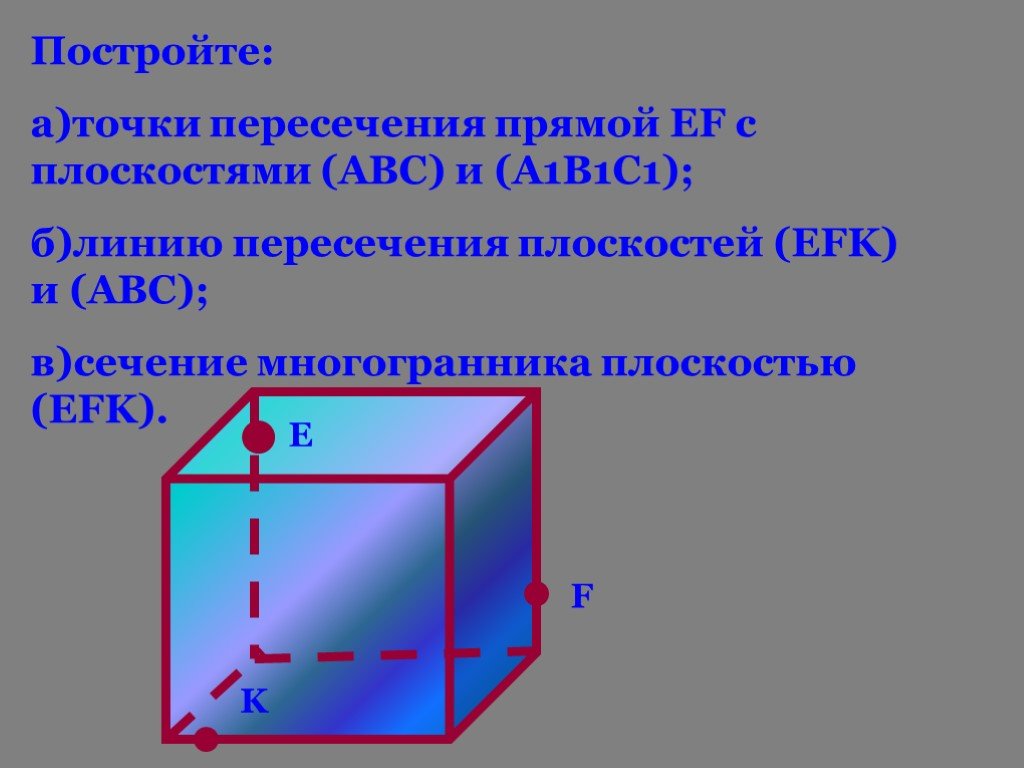
В школьном курсе стереометрии основными задачами на построение являются задачи на построение сечений пространственных фигур, а для этого необходимо ...«Скалярное произведение векторов» геометрия
Таблица значений для углов, равных 300, 450, 600. Заполните таблицу. Формулы приведения. sin( )= cos( )= -. Проверка д.з. № 1039 Диагонали квадрата ...Арифметический квадратный корень из произведения и дроби
Он есть у дерева, цветка, он есть у уравнений,. 2х + 5 = 3 КОРЕНЬ. И знак особый – радикал, с ним связан, вне сомнений. Заданий многих он итог, и ...Извлечение квадратного корня из четырёх- и трёхзначного числа
План действий: Найти квадрат числа для числа (№1), составленного из цифр тысяч (если такая есть) и сотен данного числа. Записать найденное число за ...Задачи по стереометрии
Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ...Задачи из Эфиопии
Авторы проекта А. Мезенцев К. Панова К. Г/игизиабихер А. Букреев С. Маругина Я. Ульянков. Решение задач Вы найдете на сайте школы: E-mail school-ethiopia@yandex.ru. ...Дисциплины по выбору из математического блока
Эконометрика. Наука, изучающая количественные и качественные экономические взаимосвязи с помощью математических и статистических методов и моделей. ...Движение фигур в стереометрии
Движение – геометрическое преобразование, при котором сохраняются расстояния между точками. Движением (или перемещением) фигуры называется такое ее ...Вычитание суммы из числа и числа из суммы
Устный счёт 44 ? 56 70 + 9 53 +3 +14 45 Отгадай число. Дайте характеристику этому числу. Сравни:. 24дм 5см … 7м 245см … 25дм 2м 5см … 45см. < 245см ...Вычитание однозначного числа из двузначного с переходом через разряд (викторина)
У меня сегодня всё получится! 24 11 6 + 7 20 8. Восстанови цепочку. В. О. Н 42 70 40 62 2. 64 - 9 = 55 82 - 7 = 75 Р. Компоненты действия вычитания. ...Интересные факты из истории создания геометрии
Все время, когда мы имеем дело с формой, размером, положением предмета в пространстве, мы вовлечены в геометрию. Когда доисторические люди занимались ...Конспекты
Аксиомы стереометрии
Тема урока. :. Аксиомы стереометрии. Цель урока:. ♦ рассмотреть пространственные аксиомы С1. – С3. и стереометрические аналоги. планиметрических ...Аксиомы стереометрии
. Дмитрикова Ольга Викторовна. учитель математики. МКОУ "Огорская СОШ". с.Огорь. Жиздринский район. Калужская область. класс 10. ...Куб и конструкции из кубиков
МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ. СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 67. С УГЛУБЛЕННЫМ ИЗУЧЕНИЕМ ОТДЕЛЬНЫХ ПРЕДМЕТОВ. ...Квадратный корень из произведения и дроби
Урок алгебры в 8 классе по теме. «Квадратный корень из произведения и дроби». Цель урока:. . совершенствование. функциональной грамотности учащихся ...Квадратный корень из произведения и дроби
Логинова Марина Николаевна. учитель математики. МКОУ Василёвская основная общеобразовательная школа. . Гусь-Хрустального района. ПЛАН-КОНСПЕКТ ...Квадратный корень из произведения и дроби
Конспект урока математики на тему «Квадратный корень из произведения и дроби». 1.Цель урока:. -. Образовательные. :. . изучить способы преобразования ...Квадратный корень из неотрицательного числа
Муниципальное общеобразовательное учреждение –. . Майская средняя общеобразовательная школа имени Е.Л.Чистякова. Разработка урока по теме. ...Закрепление. Вычитание из чисел 6 и 7 другого числа, на основе знаний состава чисел 6 и 7
Открытый урок по математике в 1 классе. Тема: Закрепление. Вычитание из чисел 6 и 7 другого числа, на основе знаний состава чисел 6 и 7. . . ...Даты и числа из истории Москвы
МБОУ «Степановская ООШ». Урок-экскурсия по Москве. «Даты и числа из истории Москвы». Автор: Карманова Ирина Семёновна. Д.Степановская. ...Вычитание из числа 10. Состав числа
Пакалина Наталья Алексеевна. МБОУ "СОШ №64"г. Астрахань. учитель начальных классов. Вычитание из числа 10 . Состав числа. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 сентября 2018
Категория:Математика
Содержит:42 слайд(ов)
Поделись с друзьями:
Скачать презентацию