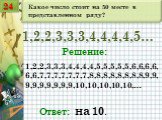
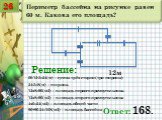
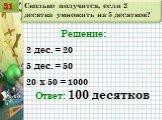
Презентация "Решение занимательных задач" (7 класс) по математике – проект, доклад
Презентацию на тему "Решение занимательных задач" (7 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 33 слайд(ов).
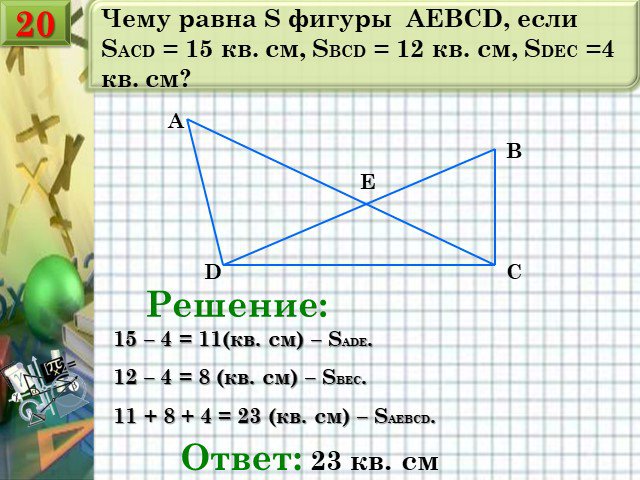
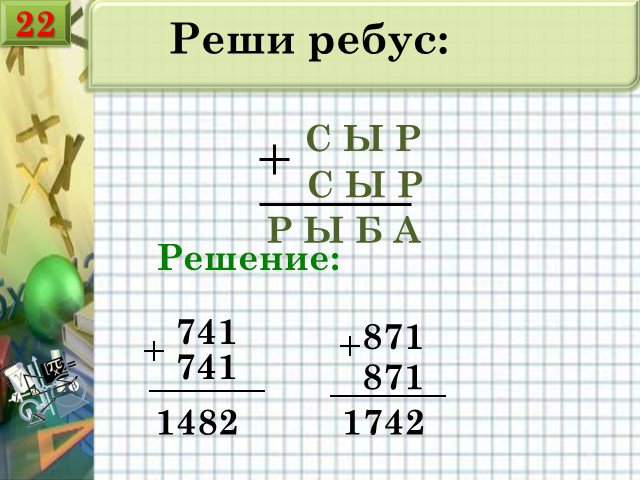
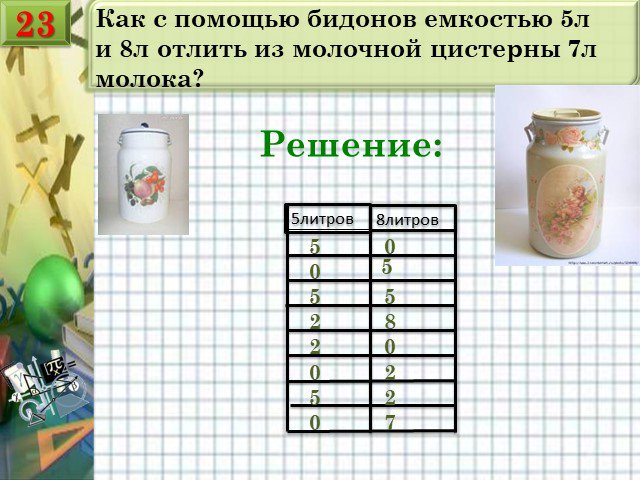
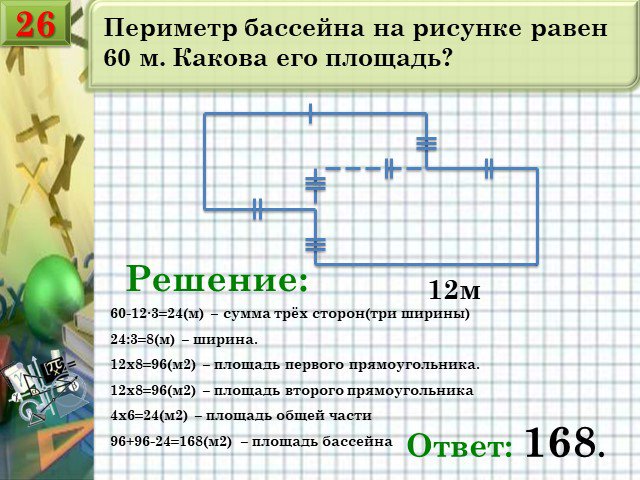
Слайды презентации
Список похожих презентаций
Вектор решение задач
Выразить векторы AM, DA, CA, MB, CD через вектор a и вектор b. № 1 Выразить векторы ВС, CD, AC, OC, OA через векторы а и b. Тивякова Л.А. № 2 Выразить ...«Решение задач по математике»
10 февраля. В классе. Задача условие вопрос решение ответ. Быстро и правильно считать. Правильно записывать решение задачи. Кричать и сердиться, когда ...Алггоритм. Решение задач
Задача 1. В урне хранится некоторое количество чёрных и белых шаров. Требуется разложить эти шары по двум корзинам чёрного и белого цвета: белые шары ...Алгебра высказываний. Решение логических задач
Задача 1: Составьте сложное высказывание в словесной форме из простых, заданных математическим формулировкам:. Высказывание А: «Учащийся Иванов хорошо ...Аксиомы стереометрии Решение задач
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ...ГИА-2014 (геометрия). Решение задач на углы.
Повторение к ГИА. http://79.174.69.4/os/xmodules/qprint/afrms.php?proj. Углы в треугольниках. № 035C64 Ответ: 8. Центральный угол AOB опирается на ...ГИА-2012. Решение задач по теме "Чтение графиков функций"
График какой из приведенных ниже функций изображен на рисунке? Задание 17 (№ 197785). Задание 17 (№ 193087). Задание 17 (№ 197695). Задание 17 (№ ...ГИА-2012. Решение планиметрических задач на нахождение углов геометрических фигур
1 3 4 5 6 7 8 9 10 11. Вашему вниманию представлено двенадцать прототипов задачи № 11 Открытого банка заданий по математике. ГИА – 2012. Два острых ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...Вычитание. Решение задач с помощью действия вычитания
Определение целей урока. Чему должны научиться сегодня на уроке? Какими свойствами вычитания будем пользоваться? Что нужно будет знать, чтобы решить ...Бинарный урок геометрии и информатики "Четырехугольники. Решение задач" Лауреат
Проверка домашнего задания. В трапеции АВСD (АD – большее основание) диагональ АС ┴СD и делит ВАD пополам, СDА=60, периметр трапеции – 20 см. Найдите ...Виды занимательных и нестандартных задач
Содержание. Что такое занимательные задачи? Когда появились занимательные задачи? Какие же существуют виды занимательных и нестандартных задач. 1. ...Графические приемы решения задач с параметрами
Решение уравнений и неравенств, содержащих параметры, является одним из самых трудных разделов элементарной математики. Для их решения обычно требуются ...Выбор действий при решении задач
Прочитай вопрос и выбери действие. Приношу свои извинения, но придётся начать заново! - · : +. На сколько 25 больше 5? У Лены 5 игрушек. У Вали в ...Алгоритм решения простых задач
. ЗАДАЧА условие Вопрос, задание. Работа в парах. 1. Налетело 5 гусей-лебедей, подхватили и унесли братца Иванушку. 2. Печка испекла девять ржаных ...Длина окружности. Площадь круга. Коллекция задач для 6 класса
. Великий древнегреческий математик Архимед (III в. до н.э.), выполнив множество измерений, установил, что длина окружности примерно в раза больше ...Блиц-опрос "Решение треугольников"
Выбери вопрос. В треугольнике АВС угол А равен 40 градусов. Внешний угол при вершине В равен 68 градусов. Найдите угол С. Угол С равен 28 градусов. ...Арксинус. Решение уравнения sin t = a
Цели. Изучить определение арксинуса числа. Изучить формулы решения простейшего тригонометрического уравнения sin t = a. Повторим. Что называется синусом ...Конспекты
Животноводство в нашем крае. Решение задач на движение
Муниципальное общеобразовательное учреждение. «Туендатская основная общеобразовательная школа». Первомайского района Томской области. ...Жизнь диких животных зимой. Решение задач
Название работы. : Интегрированный урок математика + окружающий мир по теме: «Жизнь диких животных зимой. Решение задач. » . . Автор:. Валеева ...Длина. Решение задач
Муниципальное общеобразовательное учреждение. средняя общеобразовательная школа №54. го Тольятти Самарской области. КОНСПЕКТ. урока ...Дополнение условия задачи. Решение задач
Конспект урока по математике для 1 класса по УМК 21 век. ТЕМА. :. «Дополнение условия задачи. Решение задач». ЦЕЛИ:. 1. Учить выделять части задачи, ...Деление с остатком. Решение задач на деление с остатком
. Урок математики. . «Деление с остатком. Решение задач на деление с остатком». . Учитель:. Московченко Е. Н. ...Диаграммы. Решение задач
Автор (фамилия, имя, отчество полностью) загружаемого материла. . . Гиль Наталья Николаевна. . . Место работы (полное наименование ОУ, город, ...Деление и умножение на однозначное число. Решение задач с использованием экологических понятий и терминов
Полякова Елена Александровна. учитель начальных классов. НОУ «Школа – интернат №8 ОАО «РЖД». УРОК . МАТЕМАТИКИ. (3. класс). Тема. : «. ...Деление с остатком. Решение задач
Урок математики в 3 классе по теме. «Деление с остатком. Решение задач». . Учитель начальных классов. МОУ «СОШ № 8» г.Саранск. Клёмина Татьяна ...Деление двузначного числа на однозначное и двузначное число, деление чисел с остатком, решение задач
. ТЕМА: «. Деление двузначного числа на однозначное и двузначное число, деление чисел с остатком, решение задач». . Сухова Т.А. . ...Деление двузначного числа на однозначное. Решение арифметических задач
. УРОК 15 (задания 87-93). . . Учебный предмет:. математика. Класс:. 3. . Авторы учебника:. . Истомина Н.Б., Редько З.Б., Иванова И.Ю. УМК ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:ученик Лебедев Дмитрий
Классы:
Содержит:33 слайд(ов)
Поделись с друзьями:
Скачать презентацию