Презентация "Некоторые применения теоремы Пифагора" по математике – проект, доклад
Презентацию на тему "Некоторые применения теоремы Пифагора" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 14 слайд(ов).
Слайды презентации
Список похожих презентаций
Решение теоремы Пифагора
Биография Пифагора. Письменных документов о Пифагоре Самосском не осталось, а по более поздним свидетельствам трудно восстановить подлинную картину ...Cпособы доказательства теоремы Пифагора
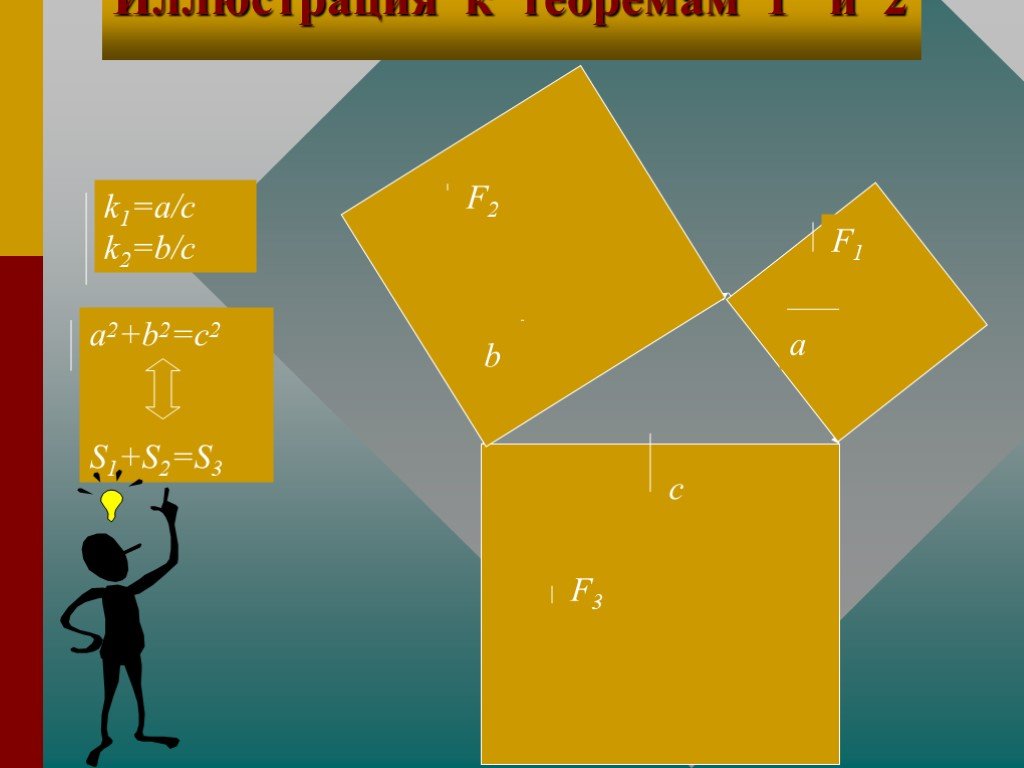
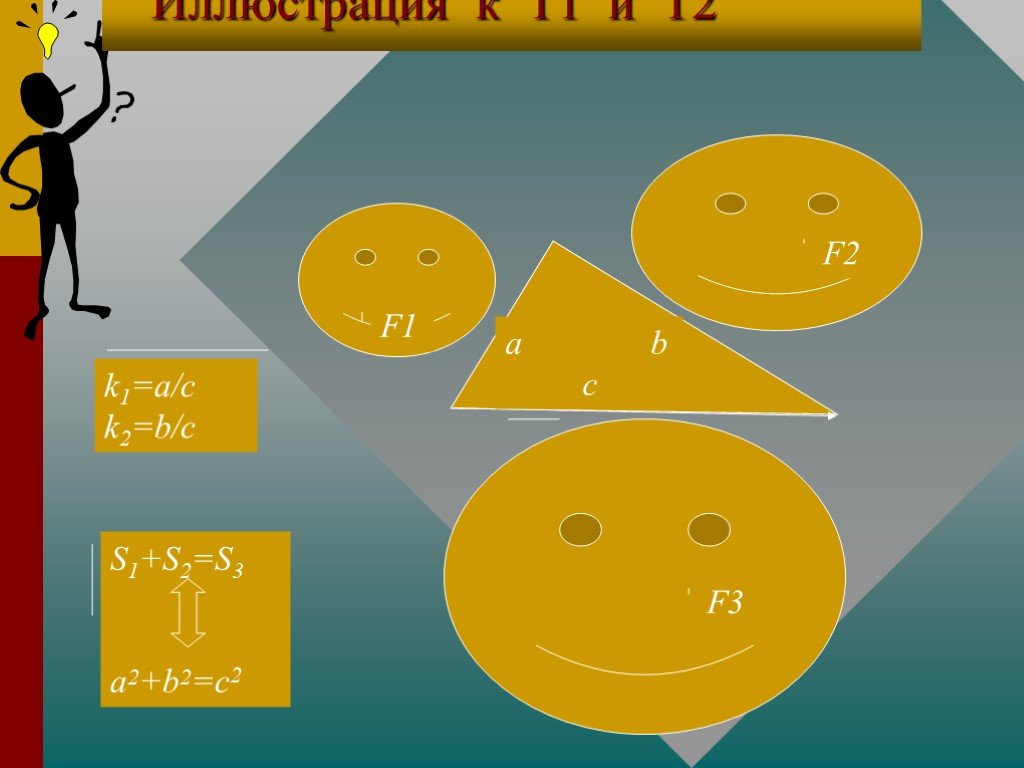
a2+b2=c2 c a b П. Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно, первым сумел его обобщить и доказать, перевести тем самым ...Доказательство теоремы Пифагора
ПОВТОРЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА. Какой треугольник называется прямоугольным? Как называются стороны прямоугольного треугольника? Какие из треугольников ...Док-ва Теоремы Пифагора
Доказательства. Пусть ABC — данный прямоугольный с треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла С (рис. 6). По определению ...Различные доказательства теоремы Пифагора
Теорема Пифагора. Структура задачи Дано. Что нужно доказать. Доказательство. CAB–прямоугольный треугольник. A B c Дано:. Доказать: SBAED=SFGAC+SHCBI. ...Различные подходы к доказательству теоремы Пифагора
На протяжении веков были даны многочисленные разные доказательства теоремы Пифагора... Чертеж к теореме Пифагора в средневековой арабской рукописи. ...Применение теоремы Пифагора в строительстве
Актуальность данного исследования. существует около 500 различных доказательств этой теорем (геометрических, алгебраических, механических), которые ...Применение теоремы Пифагора и пифагоровых троек для решения геометрических задач
Объект исследования: Теорема Пифагора и пифагоровы тройки. Предмет исследования: Применение пифагоровых троек для быстрого решения геометрических ...Тайны теоремы Пифагора
Задачи. 1. Собрать материал о истории открытия теоремы. 2. Взять интервью у учителя истории. 3. Узнать кто доказал теорему. 4. Выяснить заслугу древнегреческих ...По следам теоремы Пифагора
« Геометрия обладает двумя великими сокровищами. Первое - это теорема Пифагора, которую можно сравнить с мерой золота…» И. Кеплер. Цель: внимательно ...История открытия теоремы Пифагора
Введение. Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Пожалуй, даже те, кто в своей жизни навсегда распрощался ...Многообразие методов доказательства теоремы Пифагора
Теорема Пифагора. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Исторические сведения. Пифагор – древнегреческий ученый ...История теоремы Пифагора
Цели: 1.Расширить свои знания по истории математики. 2.Узнать больше информации, легенд, мифов о Пифагоре и его теореме. 3.Ознакомиться с другими ...История теоремы Пифагора
Цель нашего исследования. Мы хотим узнать, можно ли доказать теорему Пифагора другими способами (не так, как в учебнике)? Гипотеза Мы считаем, что ...История теоремы Пифагора
История теоремы Пифагора. Хронология развития теоремы до Пифагора:. Исторический обзор начнём с древнего Китая. Здесь особое внимание привлекает математическая ...Длина окружности. Площадь круга. Практические применения
Цели развивающие: Активизировать деятельность учащихся через разнообразные виды самостоятельной работы. Способствовать развитию долговременной памяти ...Задания по теореме Пифагора
«Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора». Иоганн Кеплер. Закончите предложение:. Прямоугольным треугольником называется ...Теорема Пифагора – математика или искусство
Зачем геометрии вдохновение? Каковы исторические факты жизни Пифагора? Какую роль сыграл Пифагор в «судьбе» знаменитой теоремы? Какое значение теорема ...Теорема Пифагора
Цель. Обобщить и систематизировать знания учащихся по теме, показать исторические истоки теоремы, учить учащихся применять полученные знания к решению ...Теорема Пифагора
Задача. . . (ок. 580 – ок. 500 г. до н.э.). Пифагор Самосский. Открытия пифагорейцев. Пифагорейцами было сделано много важных открытий в арифметике ...Конспекты
Решение задач с помощью теоремы Пифагора
Использование кейс - технологий на уроках математики. Урок геометрии в 8 классе. Тема урока: Решение задач с помощью теоремы Пифагора. Цели ...Доказательство теоремы Пифагора
Министерство образования и науки Российской Федерации. Управление образования администрации города Твери. МОУ Тверская гимназия № 10. Региональный ...Различные способы доказательства теоремы Пифагора
Ход урока:. . Здравствуйте, садитесь. Меня зовут Людмила Александровна, я рада всех Вас видеть (слайд 1). Пребудет вечной истина, как скоро. ...Теорема Пифагора
VII ВСЕРОССИЙСКИЙ КОНКУРС. ПРОФЕССИОНАЛЬНОГО МАСТЕРСТВА ПЕДАГОГОВ. «МОЙ ЛУЧШИЙ УРОК». естественно-научное направление. Муниципальное ...Теорема Пифагора
Тема урока по геометрии в 8-м классе: "Теорема Пифагора». Цели урока:. Образовательная:. обеспечить понимание доказательства теоремы Пифагора ...Теорема Пифагора
Тема урока:. Теорема Пифагора. Цели урока:. Образовательные: сформулировать и доказать теорему Пифагора,. . рассмотреть основные следствия из ...Теорема Пифагора
Урок геометрии в 8-м классе: "Теорема Пифагора". Цели урока:. Образовательная:. обеспечить понимание доказательства теоремы Пифагора и ее применение ...Изучая теорему Пифагора, изучаем её историю
Конференция по геометрии. по теме. «Изучая теорему Пифагора, изучаем её историю». Цели:. · Воспитание устойчивого интереса к изучению предмета ...Теорема Пифагора и её применение
МКОУ Новониколаевская СОШ. Барабинского района. Новосибирской области. Урок - путешествие в 8 классе по теме:. «Теорема Пифагора и её применение». ...Теорема Пифагора
Государственное бюджетное образовательное учреждение г.Москвы. . средняя общеобразовательная школа №1968. Урок для 8 класса по теме ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 сентября 2019
Категория:Математика
Содержит:14 слайд(ов)
Поделись с друзьями:
Скачать презентацию