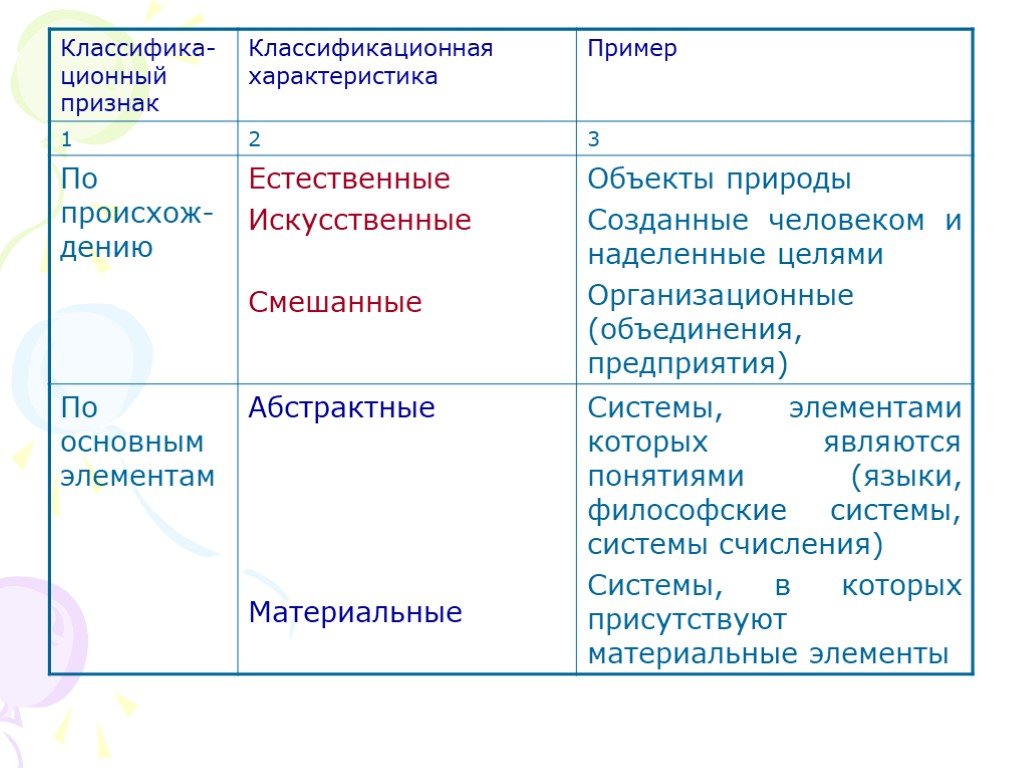
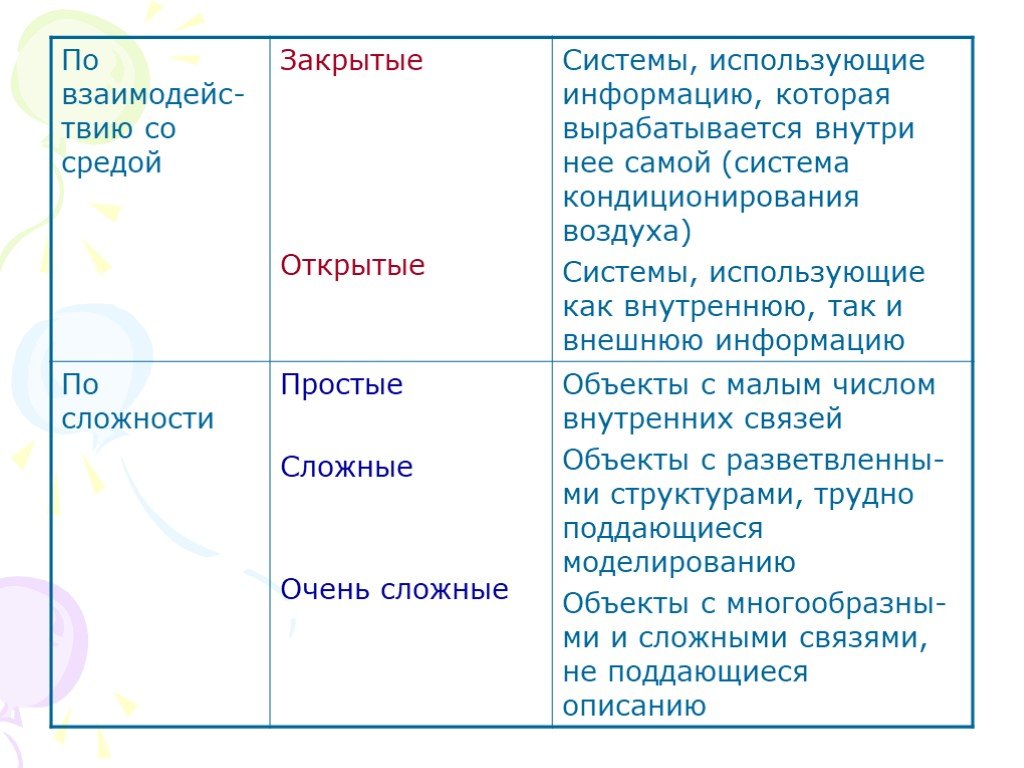
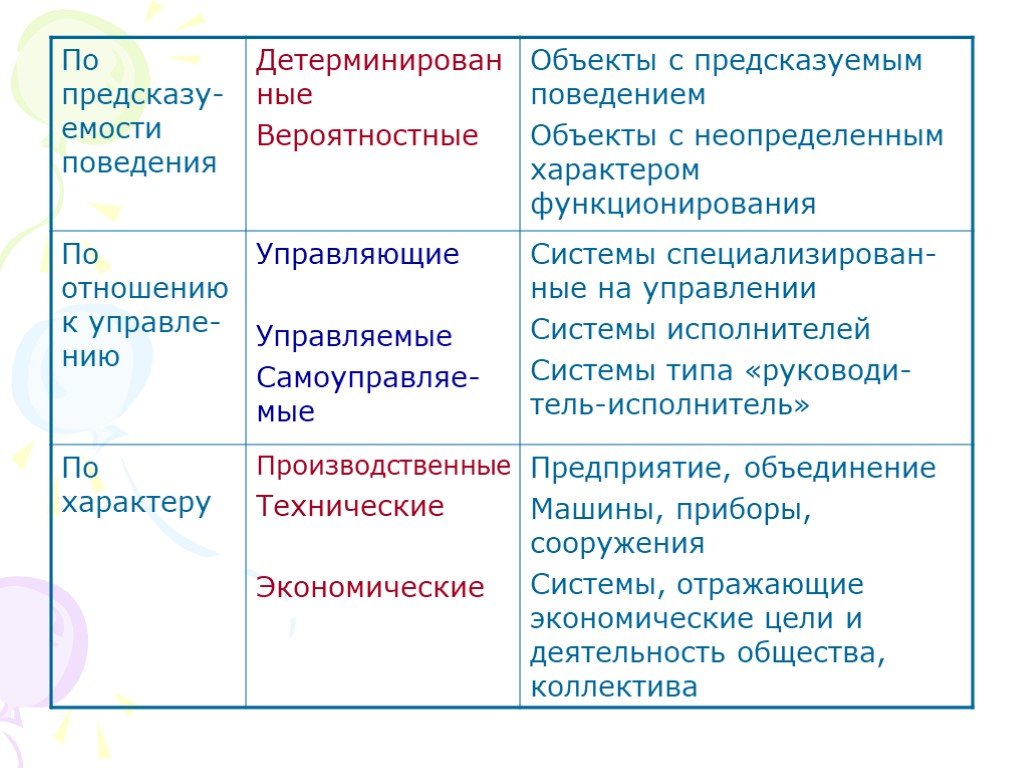
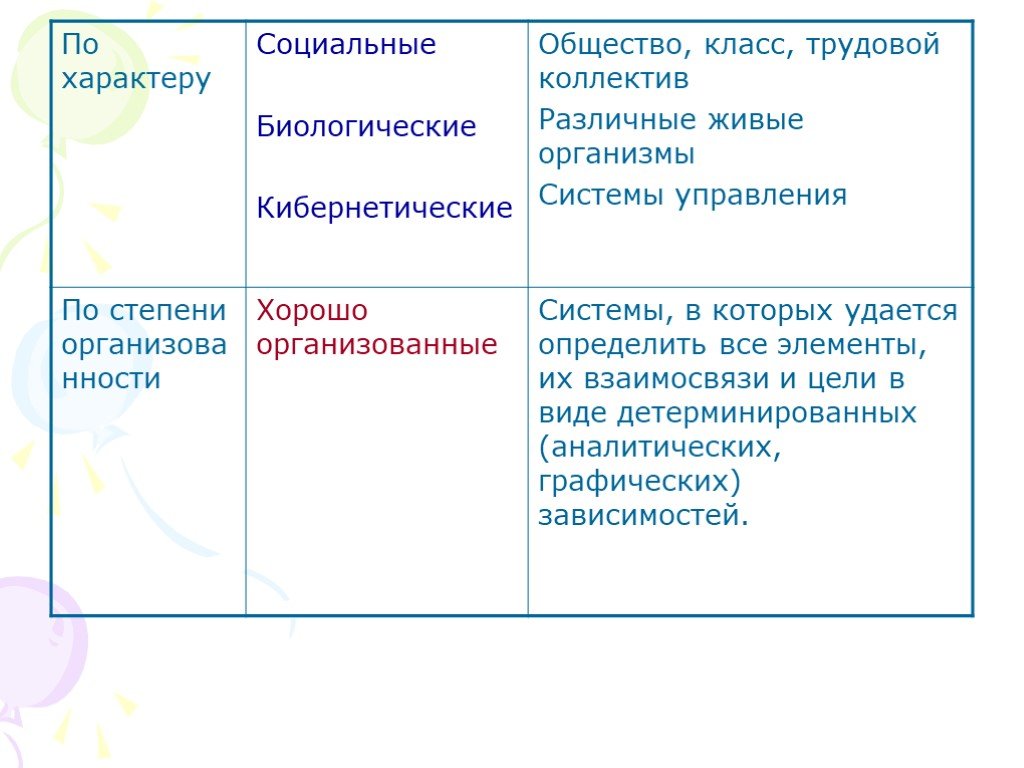
Презентация "Классификация систем" по математике – проект, доклад
Презентацию на тему "Классификация систем" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 31 слайд(ов).
Слайды презентации
Список похожих презентаций
Тела вращения. Классификация пирожных
Карточка - контроля. 7-9 баллов - оценка 3; 10 -12 баллов - оценка 4 13 баллов и выше - 5. Тела вращения Математика. Хрупкий абрис колонн попирает ...Решение систем способом подстановки
1. Вычислите. 32 ; 102 ; 122 ; ;. 2. Назовите 3 решения уравнения: а) х – у = 1; в) 6 + 0х = 2у; б) ху = 0; г) 0х + 0у = 0. 3. Выразите переменную ...Решение систем уравнений методом новой переменной
Решение систем уравнений. методом введения новой переменной переменной. Разминка! Что такое решение системы уравнений? Какие методы решения систем ...Решение систем линейных уравнений
Решение систем линейных уравнений. (урок обобщения). Устная работа. Выразите неизвестное у через х: 2х + у=11; 3х – у=9; 7х=9у; х-у=5; 2х – 2у=6; ...Решение систем неравенств
«Математика – наука о порядке» А. Уайтхед. Обучение математике через задачи – идея далеко не новая. Еще Ньютон сказал: «Примеры поучают больше, чем ...Решение неравенств и их систем
Задание 1. Установите соответствие между неравенствами и промежутками, которые являются их решением. Задание 2. Установите соответствие между промежутками ...Решение систем двух линейных уравнений с двумя переменными различными способами
Цель урока:. Продолжить формирование навыков сознательного выбора способа решения системы Развивать потребность в нахождении рациональных способов ...Графический способ решения систем уравнений
Построение графика линейной функции. Прямая линия. y = ах + b. х – любое действительное число. 1. Повторение. Построение графика функции обратной ...Графическое решение систем уравнений
Лаборатория «ТРУД». Твори, Решай, Учись, Добивайся с интересом и удовольствием! Руководители лаборатории. Начальник лаборатории: Ноумэн Ноу Мэнович ...Графический способ решения систем уравнений
Что является геометрической иллюстрацией уравнения с двумя неизвестными? y-x=2 y+x=2. y=x+2 *A(0;2) *B(-2;0). Уравнение можно рассматривать как формулу, ...Графический способ решения систем уравнений
Организационный момент; Подготовка к усвоению новых знаний; Изучение нового материала; Первичная проверка изученного материала; Первичное закрепление ...Графический способ решения линейных систем уравнений
Линейная функция – это функция вида y=kx+b , в котором k и b - действительные числа. Графиком линейной функции y=kx+b является прямая. Алгоритм ...Графический метод решения систем уравнений с двумя переменными
Обобщить графический способ решения систем уравнений; Сформировать умения графи-чески решать системы уравне-ний второй степени, привлекая известные ...Графический метод решения систем
Что называют системой уравнений? Рассмотрим два линейных уравнения: Y=-x+3 и Y=2x-3 Найдём такую пару значений (x;y), которая одновременно является ...Описание линейных дискретных систем во временной области
Дискретным называется сигнал, дискретный во времени и непрерывный по состоянию. Он описывается решетчатой функцией (последовательностью) x(nT), где ...Графическое решение систем уравнений
Правило решения системы уравнений графическим способом. Построить графики каждого из уравнений системы. Найти координаты точки пересечения построенных ...Представление числовой информации с помощью систем счисления
Система счисления. - это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых ...Динамические характеристики измерительных систем
Динамические характеристики измерительных систем. Импульсная характеристика системы Частотная характеристика и импульсная характеристика линейной ...Решение неравенств и систем неравенств с одной переменной
Повторение. 1. Какие неравенства соответствуют промежуткам:. 2. Изобразите геометрическую модель промежутков:. 3. Какие неравенства соответствуют ...Динамическое описание информационных систем
Динамическая система — математическая абстракция, предназначенная для описания и изучения систем, эволюционирующих с течением времени. Система, которая ...Конспекты
Решение систем линейных уравнений способом сложения
Муниципальное общеобразовательное учреждение. Пестравская средняя образовательная школа. Пестравского района Самарской области. ...Решение систем неравенств с одной переменной
Муниципальное общеобразовательное учреждение. «Лицей №38» г. Белгород. Урок по теме:. «Решение систем неравенств ...Решение систем линейных уравнений
Разработка урока алгебры. с использованием. интерактивной доски. по теме:. «Решение систем линейных уравнений с двумя переменными». (7 класс). ...Решение систем линейных уравнений
Тема урока: Решение систем линейных уравнений. Цель:. . образовательная: закрепление, систематизация и обобщение знаний о методах решения и исследования ...Решение систем уравнений с одной переменной
Муниципальное автономное общеобразовательное учреждение. «Средняя общеобразовательная школа №16». Города Губкина Белгородской области. ...Решение уравнений, неравенств и систем уравнений
Муниципальное бюджетное общеобразовательное учреждение. основная общеобразовательная школа№8. поселка Садового Муниципального образования Славянский ...Методы решения систем двух линейных уравнений с двумя переменными
План- конспект урока алгебры в 7 классе по теме: «Методы решения систем двух линейных уравнений с двумя переменными». Орг. момент, сообщение ...Решение систем уравнений второй степени
МОУ ООШ c. .Смышляевка. Сергейчева Людмила Алексеевна, учитель математики. Алгебра 9 класс. . . Тема урока "Решение систем уравнений второй ...Графический способ решения систем уравнений
Тема урока:. . Графический способ решения систем уравнений. Тип урока. : Урок изучения нового материала. Цели урока. :. Образовательные. ...Использование метода подстановки для решения систем уравнений
Муниципальное бюджетное общеобразовательное учреждение. «Тимковская основная общеобразовательная школа». Использование . метода . подстановки ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:23 сентября 2019
Категория:Математика
Содержит:31 слайд(ов)
Поделись с друзьями:
Скачать презентацию