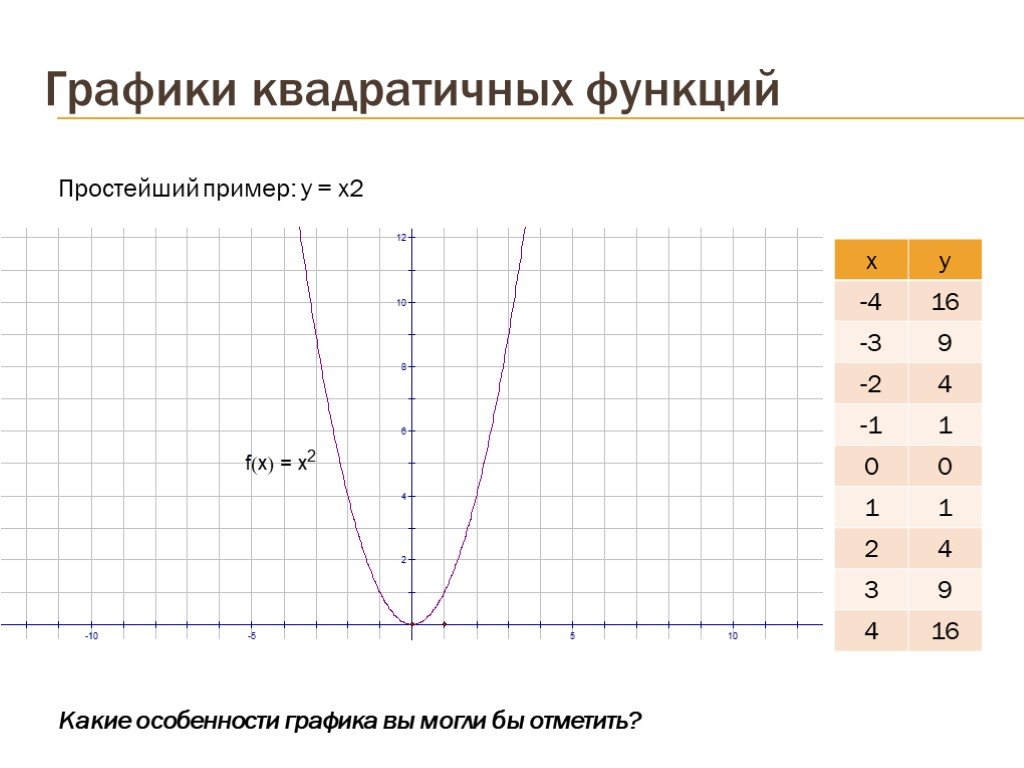
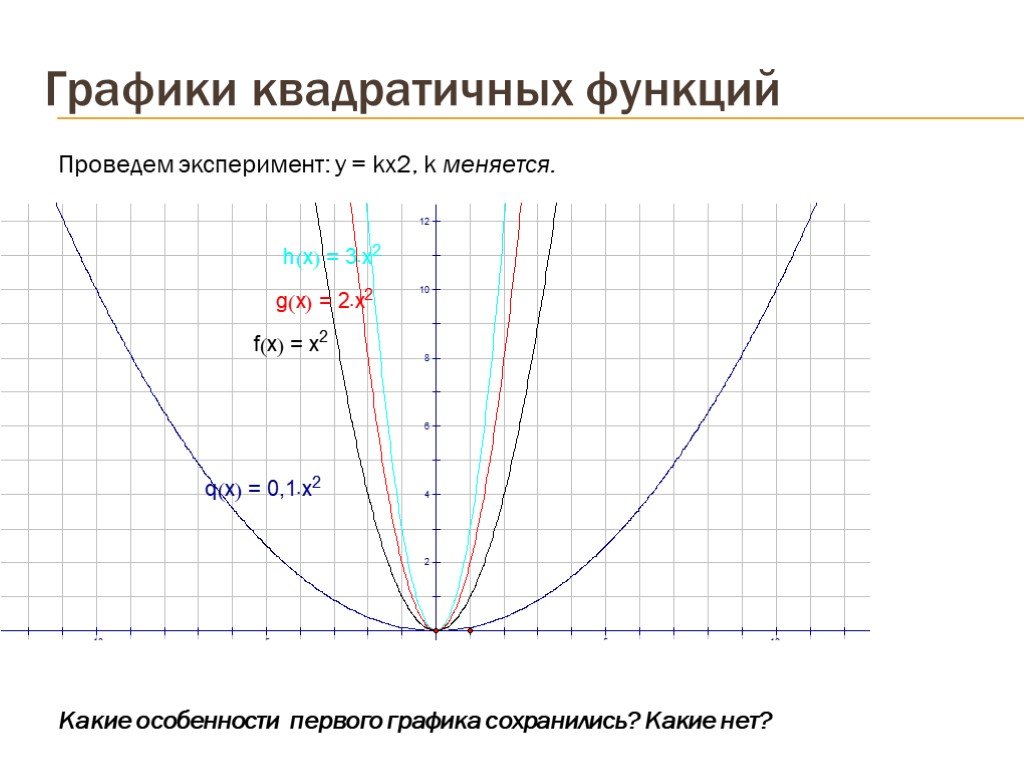
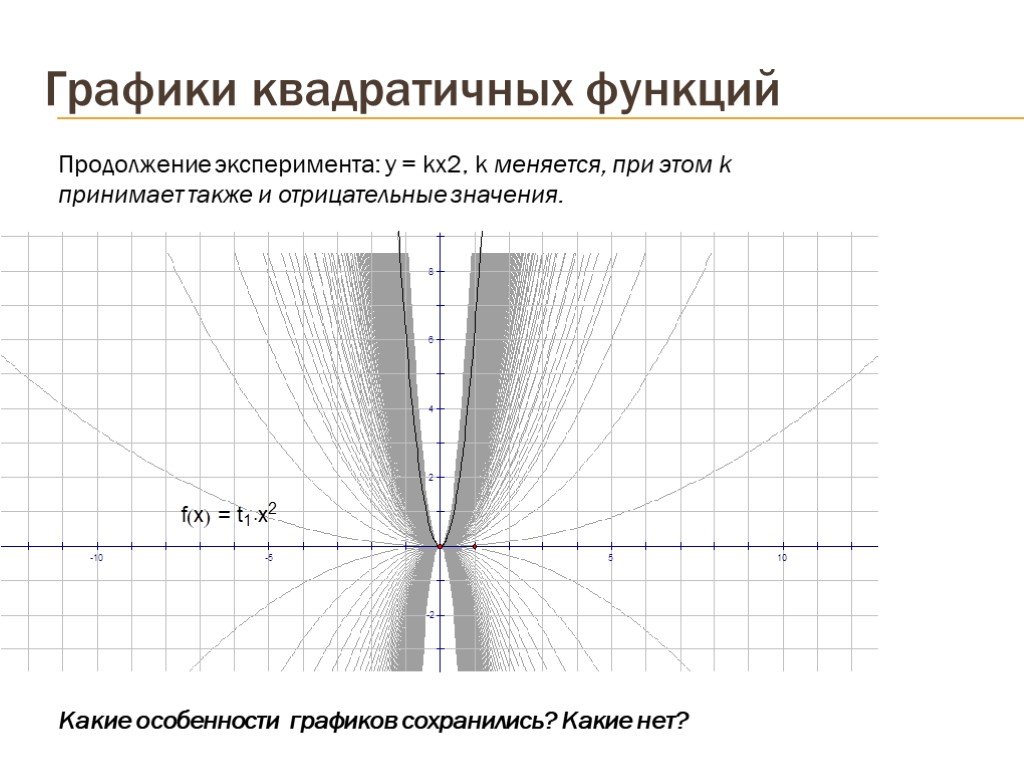
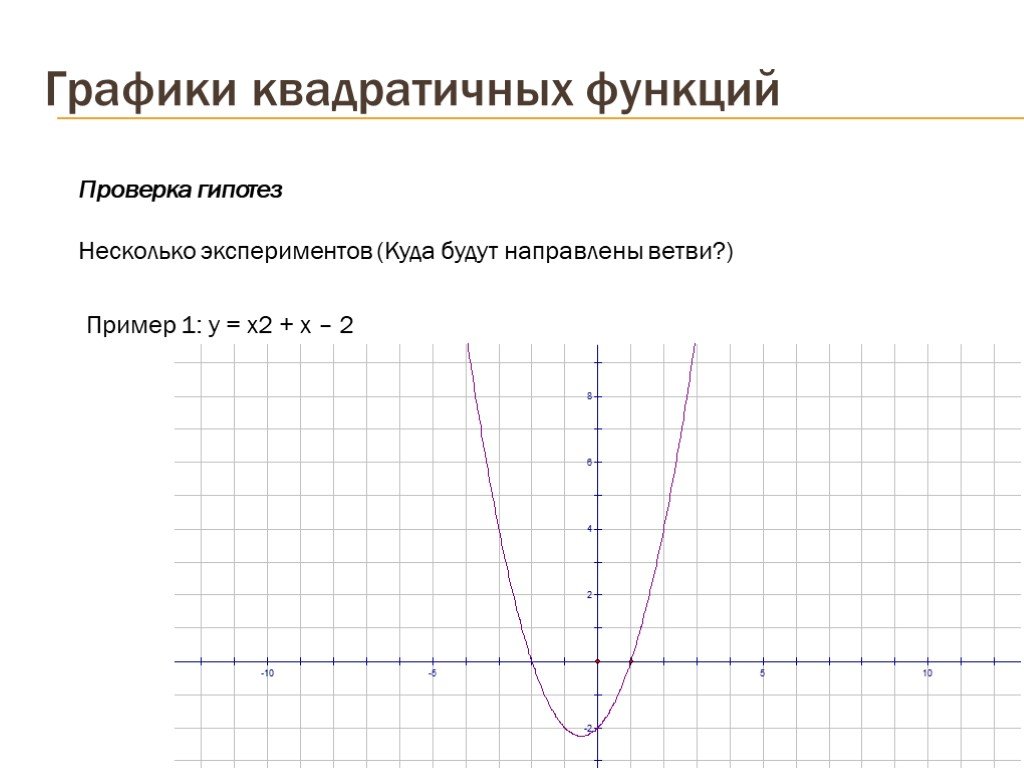
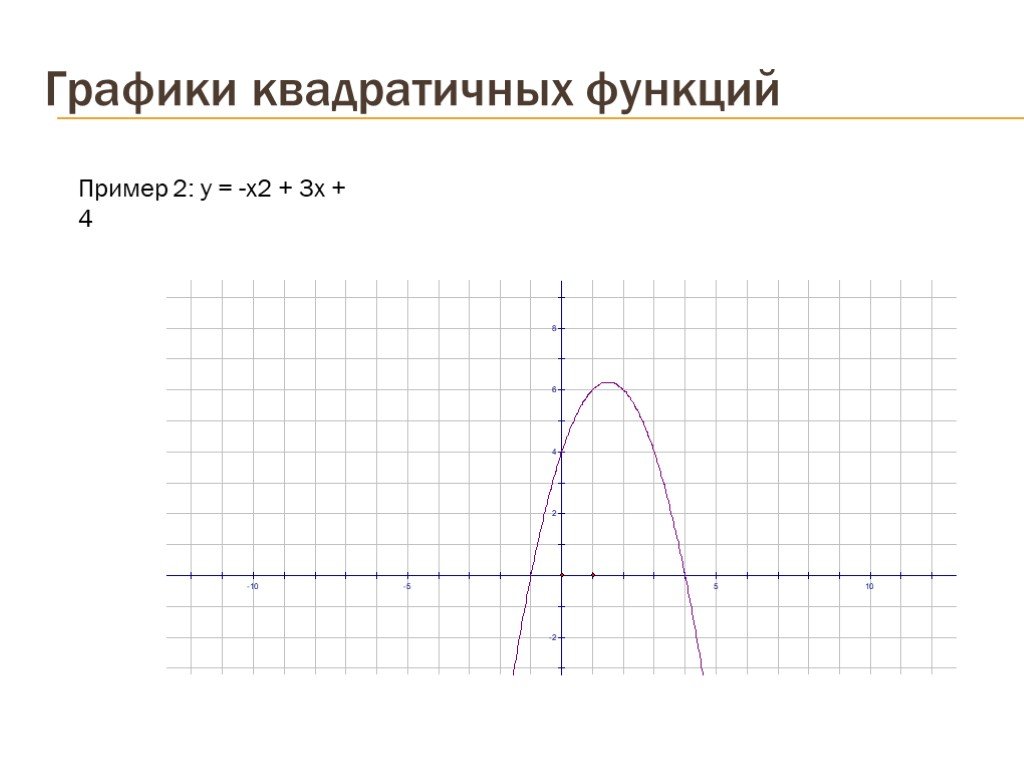
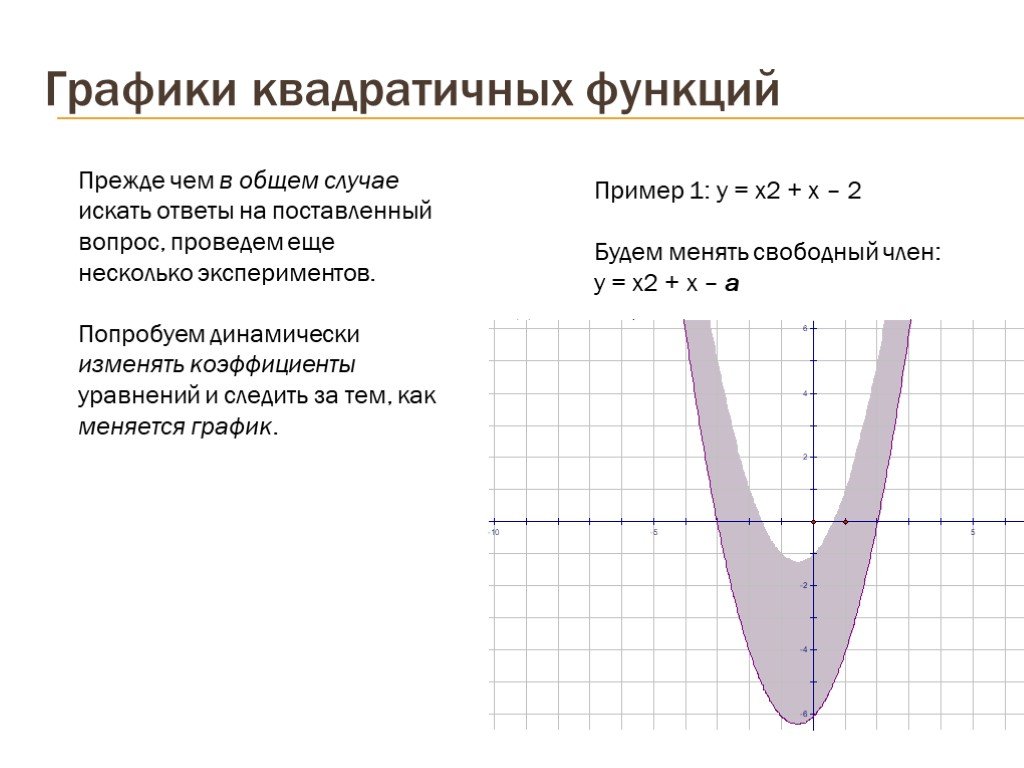
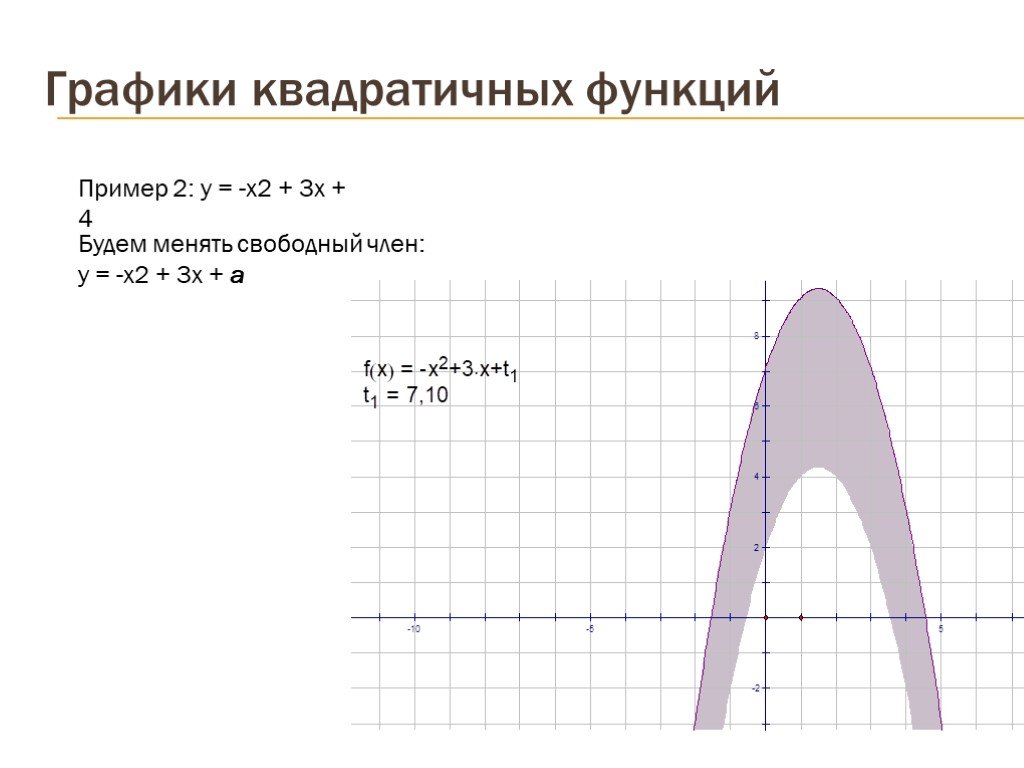
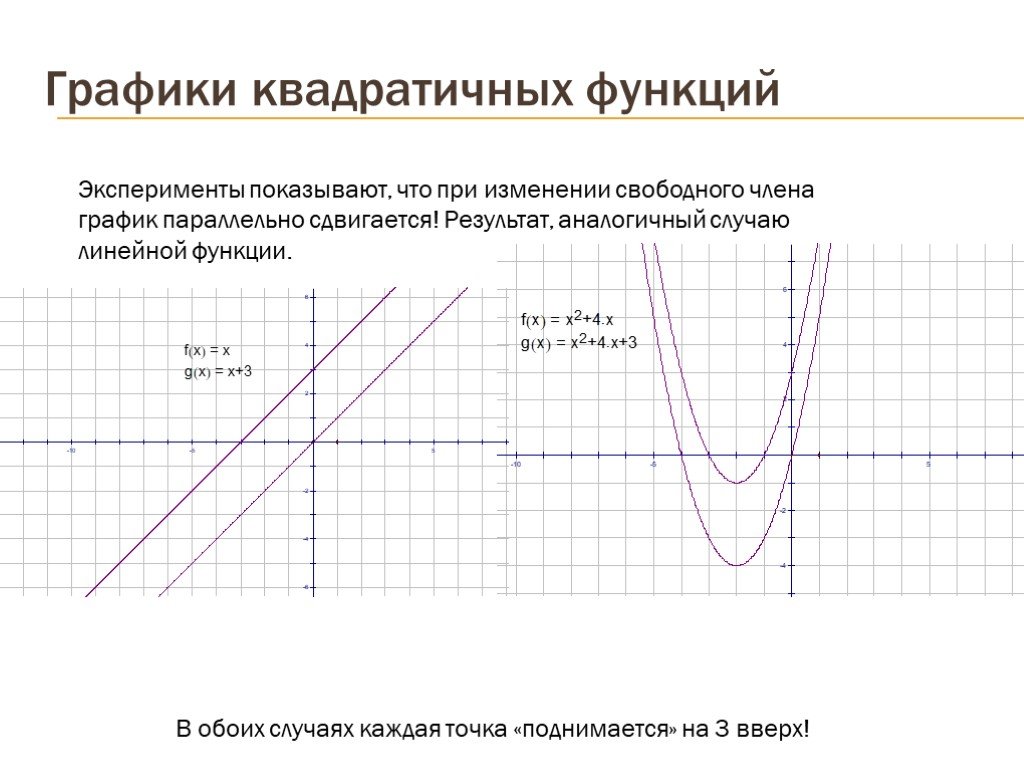
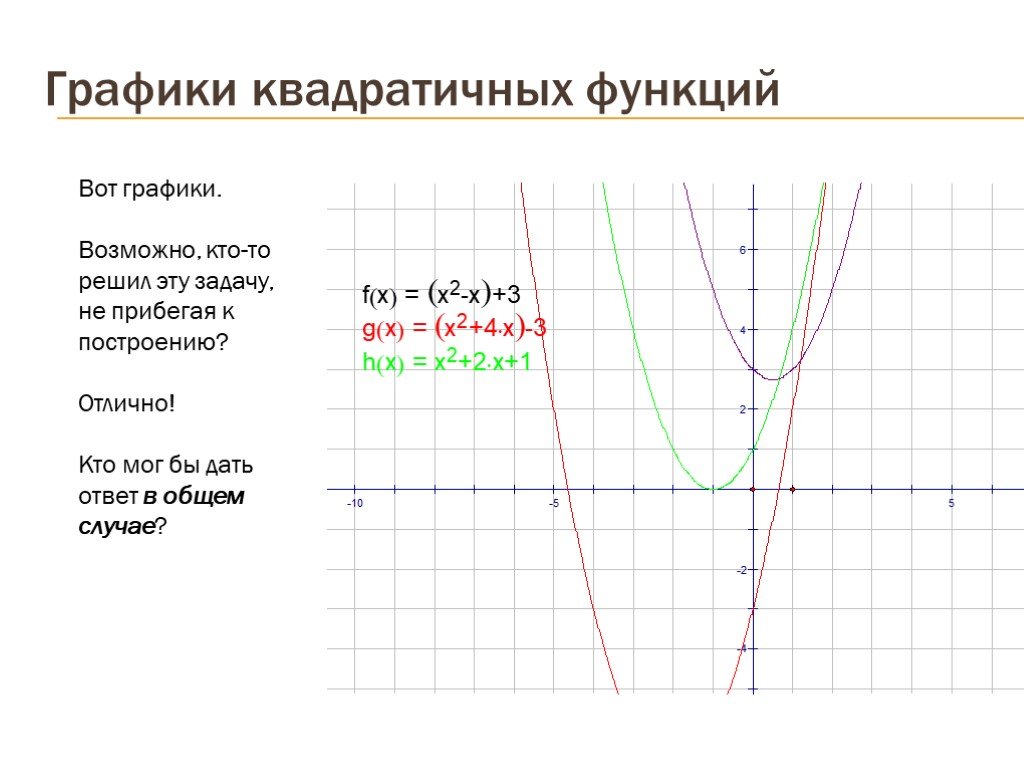
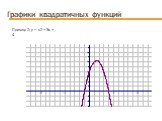
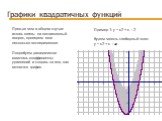
Презентация "Графики квадратичных функций" по математике – проект, доклад

Графики квадратичных функций

Учитель: Чехова Нина Григорьевна

Этапы рассмотрения Простейшие примеры Свойства графиков квадратичных функций Графики и коэффициенты уравнений – простейшие закономерности Динамические демонстрации

Простейший пример: у = х2

Какие особенности графика вы могли бы отметить?

Проведем эксперимент: у = kх2, k меняется.

Какие особенности первого графика сохранились? Какие нет?

Определение: квадратичная функция задается уравнением у = ах2 + bх + с, причем а ≠ 0 (в противном случае мы придем к случаю линейной функции).

Вопросы: Сохранится ли «форма» уже знакомой нам параболы при ненулевых b и с? Сохранится ли симметрия графика? Сохранится ли «вершина»?

Продолжение эксперимента: у = kх2, k меняется, при этом k принимает также и отрицательные значения.

Какие особенности графиков сохранились? Какие нет?

Первые гипотезы Связь формы графика с коэффициентами: Если коэффициент при х2 положительный, «ветви» параболы направлены вверх. Если коэффициент при х2 отрицательный, «ветви» параболы направлены вниз. Если коэффициент при х2 равен 0? Стоп! Получившая функция выпадает из определения квадратичных! Но закономерность, тем не менее, сохраняется!!! Возникает прямая, «ветви» которой направлены ни вверх, ни вниз! . При изменении коэффициента при х2 меняется «крутизна» графика.

Проверка гипотез Несколько экспериментов (Куда будут направлены ветви?)

Пример 1: у = х2 + х – 2

Пример 2: у = -х2 + 3х + 4

Примеры подтверждают выдвинутые нами гипотезы! Одновременно возникают новые вопросы: Всегда ли коэффициент при х2 определяет направление «ветвей» параболы? Если да, то как это доказать? Всегда ли коэффициент при х2 определяет «крутизну» графика? Если да, то как это доказать? Симметрия графика вроде бы сохраняется. Но ось симметрии уже не совпадает с осью Оу. Чем определяется ее положение? Графики перестают проходить через начало координат. Появляются новые точки пересечения с осями. Чем они определяются?

Будем шаг за шагом искать ответы на возникшие вопросы. Начнем с последнего. Вопрос №6 : «Графики перестают проходить через начало координат. Появляются новые точки пересечения с осями. Чем они определяются?»

Прежде чем в общем случае искать ответы на поставленный вопрос, проведем еще несколько экспериментов. Попробуем динамически изменять коэффициенты уравнений и следить за тем, как меняется график.

Пример 1: у = х2 + х – 2 Будем менять свободный член: у = х2 + х – а

Будем менять свободный член: у = -х2 + 3х + а

Эксперименты показывают, что при изменении свободного члена график параллельно сдвигается! Результат, аналогичный случаю линейной функции.

В обоих случаях каждая точка «поднимается» на 3 вверх!

Вернемся к вопросу №6 : «Графики перестают проходить через начало координат. Появляются новые точки пересечения с осями. Чем они определяются?» Иными словами, как найти координаты точек пересечения графика квадратичной функции с осями координат? Интересный ответ: по очереди! С какой бы оси вы начали? – В парах определите, кто чем занимается и мы через несколько минут оценим результаты. В качестве пробной функции возьмем последний пример: у = х2 + 4х + 3 Как координаты точек пересечения с осями координат связаны с коэффициентами?

Так уж получилось, что быстрее справились со своей задачи те, кто искал координаты точки пересечения графика с осью Оу. В общем-то, это неудивительно. В наших экспериментах такая точка была всегда одна! Тогда как точек пересечения с осью Ох могло быть целых две! А могло и не быть вообще!!! Для функции у = х2 + 4х + 3 точка пересечения с осью Оу имеет координаты (0; 3). Возьмем несколько других примеров. Найти координаты точки пересечения графиков функций у = х2 + 4х – 3 у = х2 – х + 3 у = х2 + 2х + 1 с осью Оу.

Вот графики. Возможно, кто-то решил эту задачу, не прибегая к построению? Отлично! Кто мог бы дать ответ в общем случае?

Совершенно верно! Координаты точки пересечения с осью Оу в общем случае, для квадратичной функции, заданной уравнением у = ах2 + bх + с, (0; с). Нужно выявить метод поиска. Шаг 1: Точка пересечения с осью Оу имеет абсциссу, равную 0. Это ясно. Шаг 2: Теперь нужно понять, как найти ординату. – Правильно, подставить абсциссу (0) в уравнение и найти у. Получим у = с! Вопрос: можно ли, несколько модифицировав, применить этот метод к поиску точек пересечения с осью Ох?

Модификация метода для поиска точек пересечения с осью Ох. Шаг 1: Точка пересечения с осью Ох имеет ординату, равную 0. Это ясно. Шаг 2: Теперь нужно понять, как найти абсциссу. – Правильно, подставить ординату (0) в уравнение и найти х. Что мы получим? Давайте сравним. Что изменилось? Каков ответ? – Его поиск требует решения квадратного уравнения 0 = ах2 + bх + с