Конспект урока «Решение уравнений нестандартными методами, используя свойства функций» по математике для 10 класса

Подготовил и провел учитель математики
МКОУ «СОШ №1» г. Поворино
Воронежской области
Карташова С. А.
2014г.
Тема урока: «Решение уравнений нестандартными методами, используя свойства функций»
Форма урока – лекция с последующим закреплением. Рассчитан на 2 урока
(Слайд №1)
Цели урока:
-
Повторить и обобщить знания по теме: «Свойства функций»
-
Научить применять функциональный метод решения уравнений
-
Развивать логическое мышление, наблюдательность
-
Воспитывать активность, творческую инициативу.
(слайд№2)
Оборудование: интерактивная доска, компьютер с презентацией.
План урока:
-
Организационный момент.
-
Мотивация учебной деятельности (сообщение темы, целей урока).
-
Актуализация опорных знаний (повторение свойств основных функций).
-
Изучение нового материала (функциональный метод решения уравнений).
-
Закрепление знаний (решение упражнений).
-
Подведение итогов. Оценки.
Ход урока.
Учитель:
Для решения большинства уравнений, встречающихся на экзаменах, достаточно владеть школьным курсом математики, но при этом необходимо уметь решать не только с помощью стандартных приемов, предназначенных для вполне определенных типов уравнений, но и «нестандартными» методами, о которых мы и поговорим сегодня на уроке. Одним из таких методов решения уравнений является функциональный, основанный на использовании свойств функций. В отличие от графического метода, знание свойств функций позволяет находить точные корни уравнения, при этом не требуется построения графиков функций. Использование свойств функций способствует рационализации решения уравнений.
(слайд№3)
Ответим на вопросы:
-
Что называется уравнением?
-
Что называется корнем уравнения?
-
Что значит решить уравнение?
-
Что называется функцией?
-
Что называется областью определения функции?
-
Что называется областью значений функции?
(слайд №4)
Рассмотрим (слайд №5)
ПРИМЕР 1. Решите уравнение:
![]()
Решение: ОДЗ: ![]()
Ответ: решений нет.
(слайд №6)
ПРИМЕР 2. Решите уравнение:
![]()
Решение: ОДЗ: ![]()
ОДЗ состоит из одной точки х=1. Остается проверить, является ли х=1 корнем уравнения. Подставив, видим, что х=1 – корень уравнения.
Ответ: х=1.
Учитель:
Иногда оказывается достаточным рассмотреть не всю область определения функции, а лишь ее подмножество, на котором функция принимает значения, удовлетворяющие некоторым условиям (например, только неотрицательные значения)
(слайд №7)
ПРИМЕР 3.
![]()
Решение. Найдем пересечение областей определения функций в правой и левой частях уравнения:
D1![]()
![]()
Ограничим множество D, учитывая, что левая часть уравнения неотрицательна, и, значит, такой же должна быть правая частью Для этого нужно рассмотреть пересечение множества D с множеством решений неравенства ![]() , то есть с множеством
, то есть с множеством ![]() . Следовательно, достаточно рассмотреть уравнение на множестве
. Следовательно, достаточно рассмотреть уравнение на множестве ![]() .
.
Подстановкой убеждаемся, что оба элемента служат решением уравнения.
Ответ: -3; 2.
(слайд №8)
ПРИМЕР 4.
![]()
Решение.
-
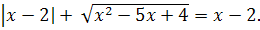
-
Так как левая часть уравнения неотрицательна, то
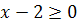 .
. -
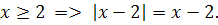
-
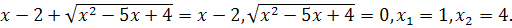
С учетом того, что ![]() корнем уравнения является х=4.
корнем уравнения является х=4.
Ответ: 4.
Учитель:
Перейдем к решению уравнений с использованием понятия области значений функции.
(слайд №9-№10)
(слайд №11)
ПРИМЕР 1.
![]() .
.
Решение. Так как ![]() , то уравнение не имеет решения.
, то уравнение не имеет решения.
Ответ: нет решений.
ПРИМЕР 2.
![]() .
.
Решение. ОДЗ: ![]()
Ответ: нет решений.
Учитель:
Если функция f(x) на промежутке Х ограничена сверху, а функция g(x) ограничена снизу, то уравнение f(x) = g(x) равносильно системе ![]()
(слайд №12)
ПРИМЕР 3.
![]()
Решение. По определению, ![]()
![]()
![]()
Равенство достигается, если 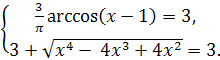
Решим первое уравнение системы:
arccos (x-1) =π, x-1 = -1, x=0.
При х=0 второе уравнение обращается в верное числовое равенство.
Следовательно, решением системы и данного уравнения является х=0.
Ответ: 0.
(слайд №13-14)
ПРИМЕР 4.
![]() .
.
Решение.
-
ОДЗ:
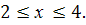
-
Рассмотрим функцию
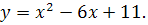 Её графиком является парабола с вершиной А(3;2), тогда
Её графиком является парабола с вершиной А(3;2), тогда 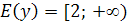 .
. -
Рассмотрим функцию
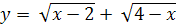
Найдем максимум этой функции на промежутке (2;4) с помощью производной.
![]()
![]() =0,
=0, ![]()
g


 ’ + -
’ + -

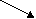
g 2 3 4 x
max
g(3)=2. Имеем ![]()
Тогда данное уравнение равносильно системе ![]()
Решив первое уравнение системы, получим х=3, проверкой, подставив во второе уравнение убедимся, что х=3 – решение системы и данного уравнения.
Ответ: 3.
(слайд №15)
Учитель:
Этот метод часто встречается на ЕГЭ по математике. Данный метод заключается в том, что одна часть уравнения ограничена сверху неким числом М, а другая часть уравнения ограничена снизу этим же числом М. Число М принято называть мажорантой, а этот метод - методом мажорант. В методе мажорант, как вы уже догадались надо хорошо понимать, что такое функция, уметь исследовать свойства функций.
(слайд №16)
Упражнения для закрепления, выработка умений и навыков.
Класс делится на 2 группы по вариантам.
1 вариант.
Докажите, что уравнение не имеет корней.
Решить уравнения:
Ответ: -0,5.
Ответ: 4,25.
Ответ: 2.
2 вариант.
Докажите, что уравнение не имеет корней.
-
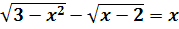 ;
; -
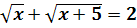
Решить уравнения:
Ответ: нет решений
Ответ:2,6.
Ответ: 2.
Учитель:
Мы сегодня рассмотрели нестандартный метод решения уравнений, используя свойства функций, который применим и для решений неравенств, но об этом мы поговорим на нескольких последующих занятиях.
Подведение итогов, оценки.
(слайд №17)
Домашнее задание:
-
arcsin (x + 2) +
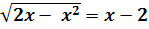 .
. -
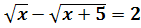
-
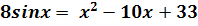
-
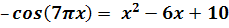
-
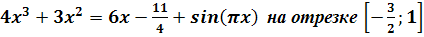
-
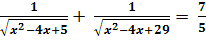
Здесь представлен конспект к уроку на тему «Решение уравнений нестандартными методами, используя свойства функций», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

