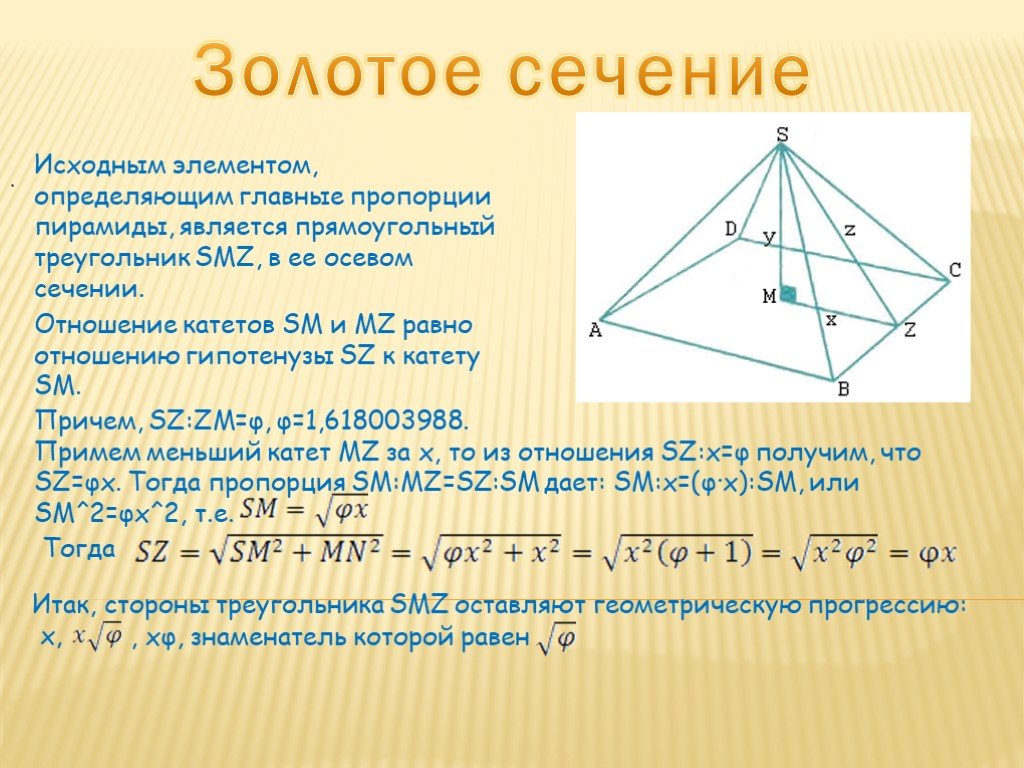
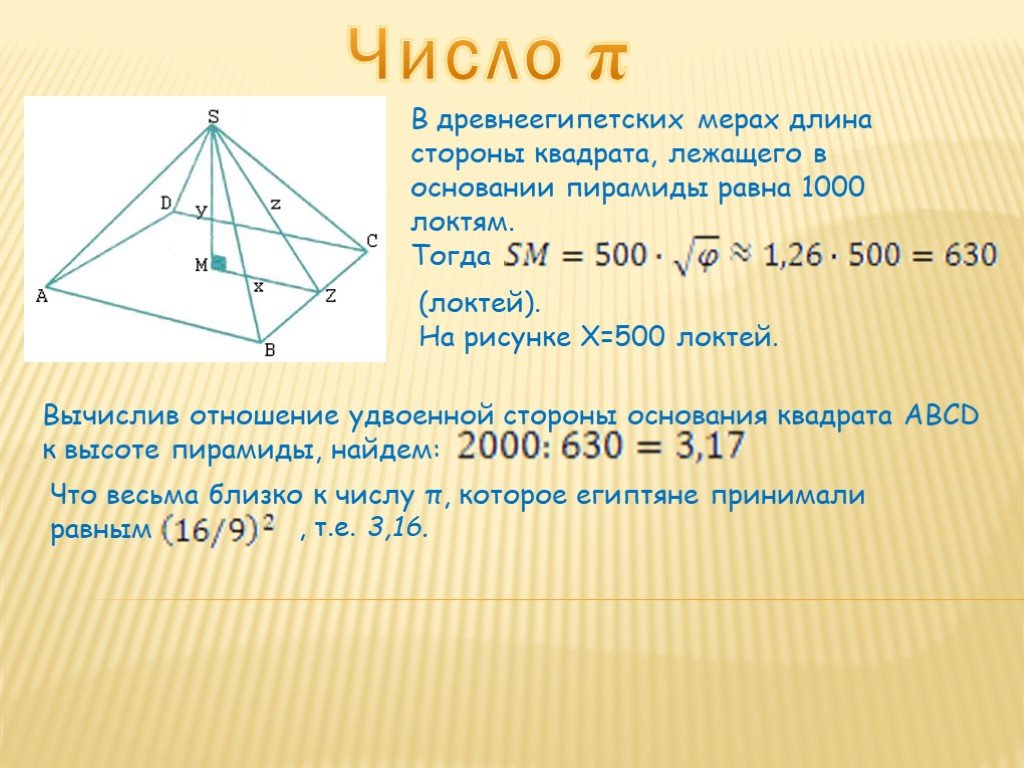
Презентация "Геометрия египетских пирамид" – проект, доклад
Презентацию на тему "Геометрия египетских пирамид" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 10 слайд(ов).
Слайды презентации
Список похожих презентаций
Геометрия пирамида
Цель. Обобщить, расширить и углубить сведения о пирамиде. Задачи:. Изучить дополнительные источники и собрать исторический и занимательный материал ...Геометрия вокруг нас. Пирамида
Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции. Первый, кто установил, чему ...Геометрия «Пирамида»
Бертран Рассел. Математика владеет не только истиной, но и высшей красотой-красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному ...Геометрия параллелограмм
Цели урока:. Продолжите предложение: При пересечении двух параллельных прямых третьей секущей…. а c b 1 + 2 = 180 1 2. накрест лежащие углы равны. ...Геометрия на вольном воздухе
Жители Древнего Египта задались вопросом: «Как найти высоту одной из громадных пирамид?» Фалес нашёл решение этой задачи. Он воткнул длинную палку ...Геометрия Лобачевского
Цель урока. Познакомить учащихся с неевклидовой геометрией , ее создателями, некоторыми теоремами геометрии Лобачевского. Расширение представлений ...Геометрия краткий курс
Содержание. Введение. Основная цель. Начальные геометрические сведения. Точки, прямые, отрезки. Луч и угол. Градусная мера угла. Смежные и вертикальные ...Геометрия и искусство
Вопрос о предпосылках прекрасного, о роли математики в искусстве волновал еще древних греков, причем свой интерес они унаследовали от предшествующих ...Геометрия Евклида
Древнегреческий математик. Родина - Афины Ученик Платона Научная деятельность протекала в Александрии (3 в. до н. э.), и ее расцвет приходится на ...Повторение «Решение треугольников» Геометрия
Теорема синусов. Синусы углов треугольника пропорциональны противоположным сторонам. а в с С В А. Теорема косинусов. Для треугольника АВС справедливо ...Геометрия «Параллельность прямой и плоскости»
Параллельные прямые. Параллельные прямые – две прямые в пространстве, которые лежат в одной плоскости и не пересекаются. Параллельность прямых обозначается ...Геометрия «Векторы»
Понятие вектора. Многие физические величины, характеризуются не только своим числовым значением, но и направлением в пространстве. Такие физические ...Геометрия «Аксиома параллельных прямых»
«Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение». (В. Произволов). ...Геометрия
1. Построить A. 2. Построить окружность произвольного радиуса с центром в вершине A. . . 4. Построить две окружности равного радиуса с центрами ...Геометрия
Учёные, внесшие вклад в развитие геометрии. Фалес Древнегреческий философ и математик, астроном и физик, путешественник и торговец, а также военный ...Геометрия
178' 179' 180' 181'. Задача №1 А В С а 1 2 Дано: АВС а АС Найти: L 1+L 2 +L 3 4 5 Ответ: L1+L2+L3= 180'. "Теорема о сумме углов треугольника.". 1 ...Геометрия четырехугольник
«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия». Эти слова, сказаны великим французским ...ГИА 2013. Модуль Геометрия №13
Повторение(3) Ответ: 23. Укажите номера верных утверждений. 1.Через любые три различные точки плоскости можно провести единственную прямую. 2.Если ...Геометрия «Параллельный перенос»
Упражнение 1. Докажите, что параллельный перенос является движением. Доказательство. Пусть параллельный перенос на вектор переводит точки A и B соответственно ...Страна "Геометрия"
Темнеет.... Бабушка-математик стала рассказывать сказку детям о стране Геометрии. В этой стране жили странные существа такие как: Теоремы, треугольники ...Конспекты
Геометрия треугольника
Тема урока:. . «Геометрия треугольника». Тип урока: обобщающий урок по курсу геометрии. . Форма проведения урока: урок - бенефис». Цель урока:. ...Геометрия окружности
Урок математики в 9 классе. учителя МОУ «СОШ № 20» г. Энгельса. Милюткиной Людмилы Николаевны. и учителя математики МОУ «СОШ № 21» г. Энгельса. ...Геометрия вокруг нас…
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа № 18. Кировский район городской округ город Уфа. . ...Геометрия вокруг нас
Разработала: Ильенко Анжела Владиславовна. Учитель начальных классов МБОУ СОШ №2 г. Стрежевого Томской области. Занятие для учеников 4х кл. по теме ...Геометрия в природе
Класс. : 8. Тема. «Геометрия в природе. ». Тип урока. : урок творческого развития. Цели:. Общеобразовательные:. 1. Систематизировать знаний ...Геометрия в ГИА
Сигайло Елена Валерьевна, учитель математики. МБОУ. . «Средняя общеобразовательная школа пос. Октябрьский». . пос. Октябрьский Лысогорского района ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:26 августа 2019
Категория:Математика
Содержит:10 слайд(ов)
Поделись с друзьями:
Скачать презентацию