Презентация "Геометрия пирамида" – проект, доклад
Презентацию на тему "Геометрия пирамида" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 42 слайд(ов).
Слайды презентации
Список похожих презентаций
Геометрия «Пирамида»
Бертран Рассел. Математика владеет не только истиной, но и высшей красотой-красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному ...Геометрия вокруг нас. Пирамида
Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции. Первый, кто установил, чему ...Геометрия четырехугольник
«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия». Эти слова, сказаны великим французским ...Геометрия на службе у архитектуры
Работу выполнила: Фёдорова Ирина Петровна, ученица 7 «А» класса МКОУ СОШ №4 руководитель учитель математики Терентьева Ольга Анатольевна городского ...Геометрия повторение
Назовите изображённые фигуры. отрезок луч прямая. Вспомните их определения. Какая фигура называется углом? Какой угол называется прямым, острым, тупым? ...Геометрия
Содержание:. Координаты вектора Связь между координатами вектора и координатами его начала и конца Уравнения окружности и прямой Синус, Косинус, Тангенс ...Геометрия Лобачевского
Сотни профессиональных геометров разных времён и народов, тысячи любителей математики в течение 20-х веков искали доказательство пятого постулата. ...Правильная пирамида
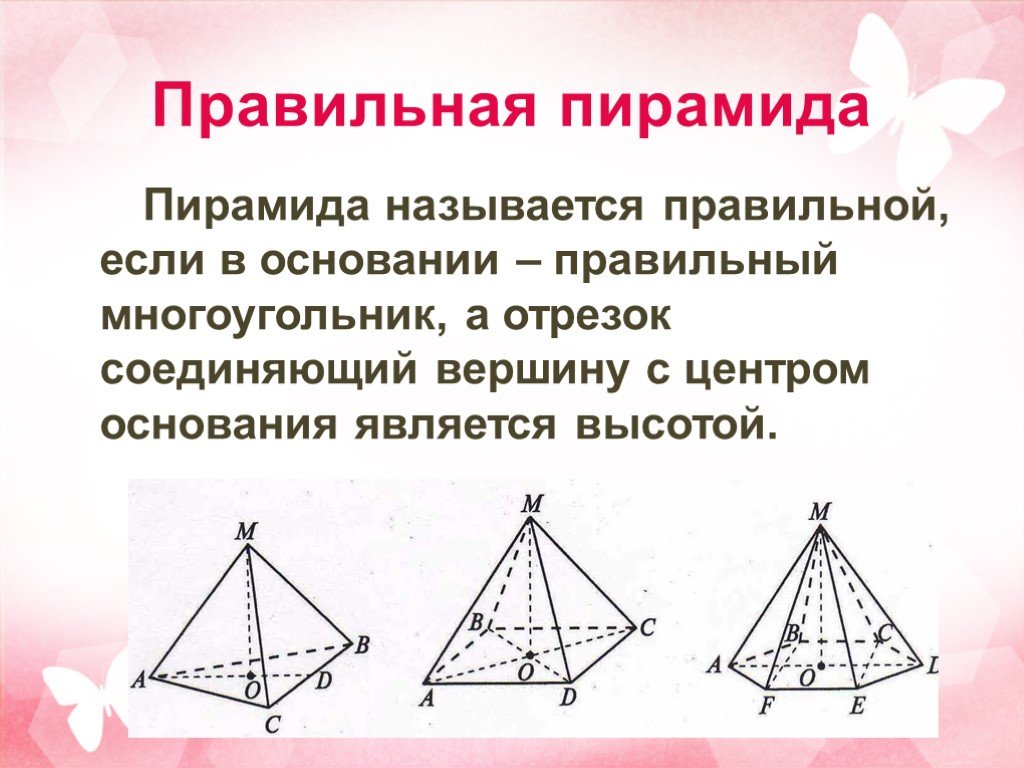
Цели урока:. введение понятия правильной пирамиды; рассмотрение свойств правильной пирамиды; введение понятия апофема; рассмотрение задач на нахождение ...Фигура пирамида
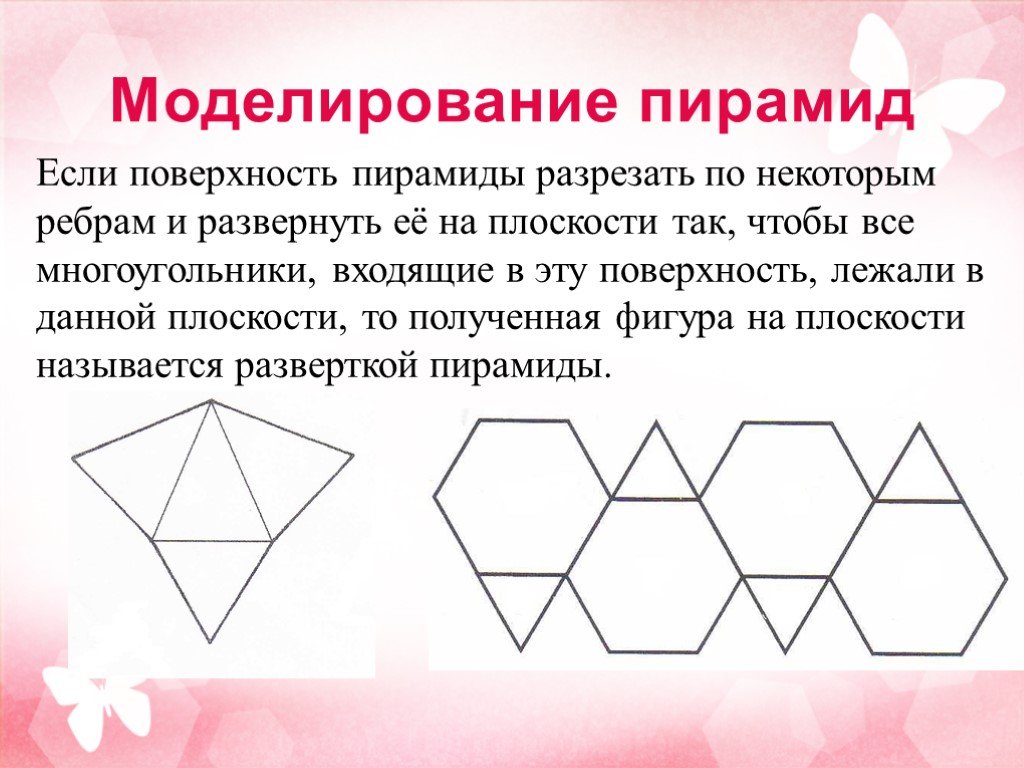
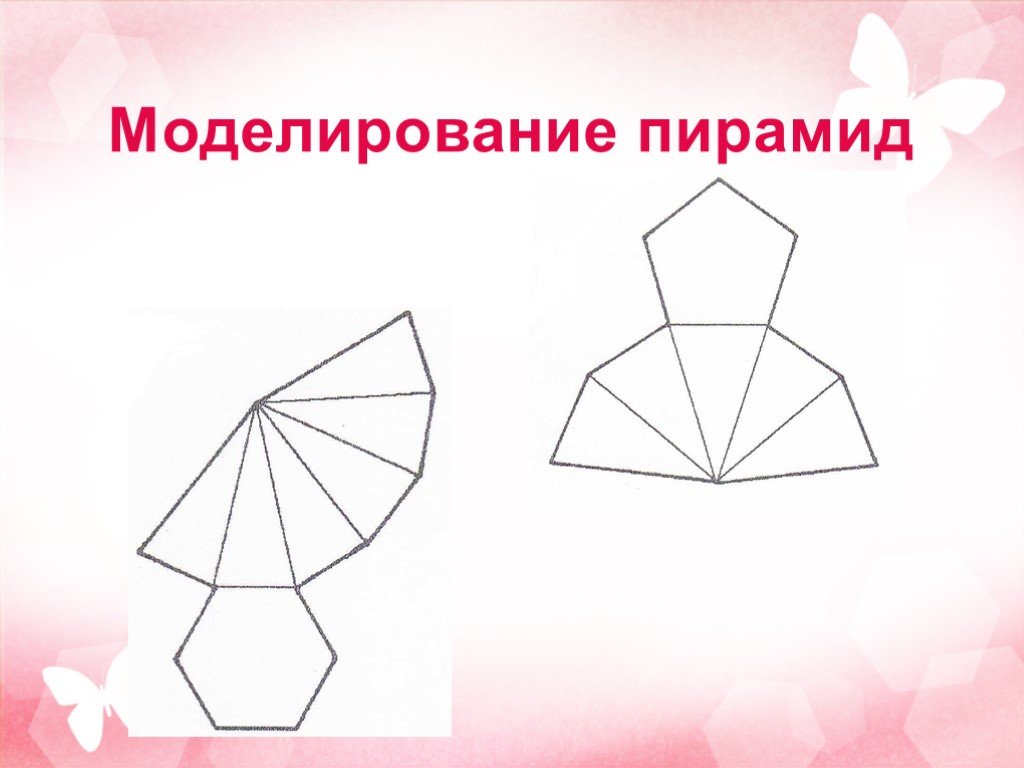
Содержание. 1 История развития геометрии пирамиды 2 Элементы пирамиды 3 Развёртка пирамиды 4Свойства пирамиды 5Теоремы, связывающие пирамиду с другими ...Геометрия «Векторы»
Понятие вектора. Многие физические величины, характеризуются не только своим числовым значением, но и направлением в пространстве. Такие физические ...Геометрия «Параллельность прямой и плоскости»
Параллельные прямые. Параллельные прямые – две прямые в пространстве, которые лежат в одной плоскости и не пересекаются. Параллельность прямых обозначается ...Геометрия
1. Построить A. 2. Построить окружность произвольного радиуса с центром в вершине A. . . 4. Построить две окружности равного радиуса с центрами ...Геометрия «Аксиома параллельных прямых»
«Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение». (В. Произволов). ...Геометрия
Учёные, внесшие вклад в развитие геометрии. Фалес Древнегреческий философ и математик, астроном и физик, путешественник и торговец, а также военный ...Геометрия
178' 179' 180' 181'. Задача №1 А В С а 1 2 Дано: АВС а АС Найти: L 1+L 2 +L 3 4 5 Ответ: L1+L2+L3= 180'. "Теорема о сумме углов треугольника.". 1 ...Геометрия
Həndəsİ fiqurlarIn qruplaşdIrIlmasI. TƏDQIQAT SUALI. BÜTÜN HƏNDƏSI FIQURLAR EYNI OLSA YDI NƏ OLARDI? . 1. Şəklə bax! Kvadratları göy, üçbucağı sarı, ...ГИА 2013. Модуль Геометрия №13
Повторение(3) Ответ: 23. Укажите номера верных утверждений. 1.Через любые три различные точки плоскости можно провести единственную прямую. 2.Если ...Геометрия «Параллельный перенос»
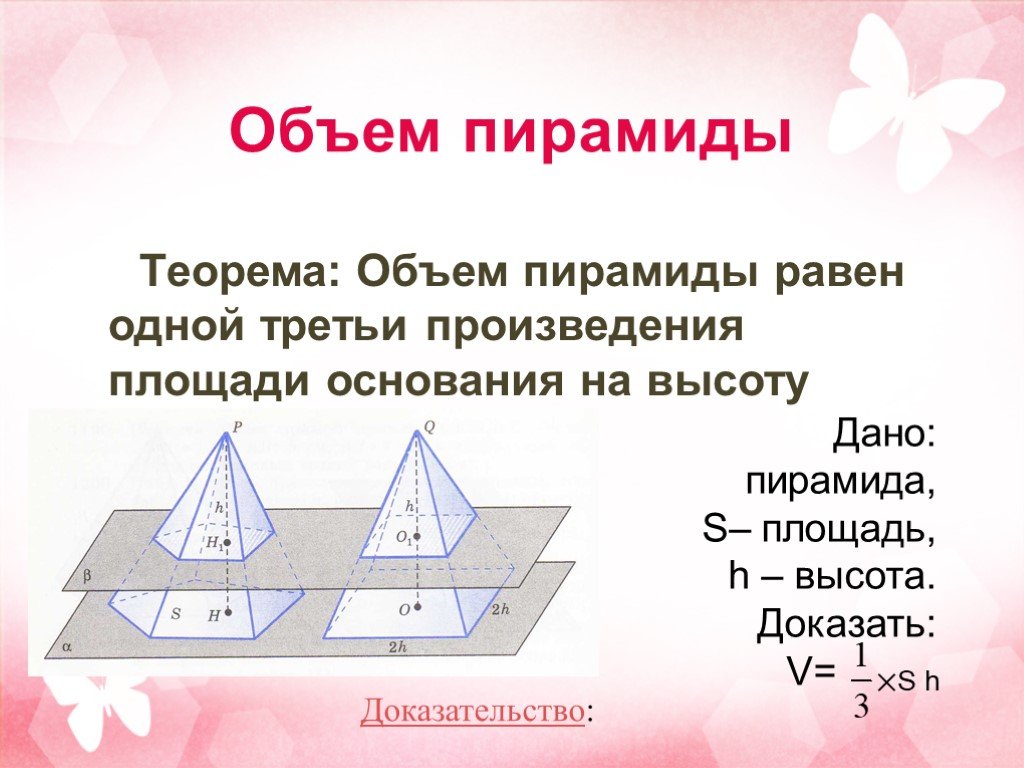
Упражнение 1. Докажите, что параллельный перенос является движением. Доказательство. Пусть параллельный перенос на вектор переводит точки A и B соответственно ...Пирамида. Усечённая пирамида
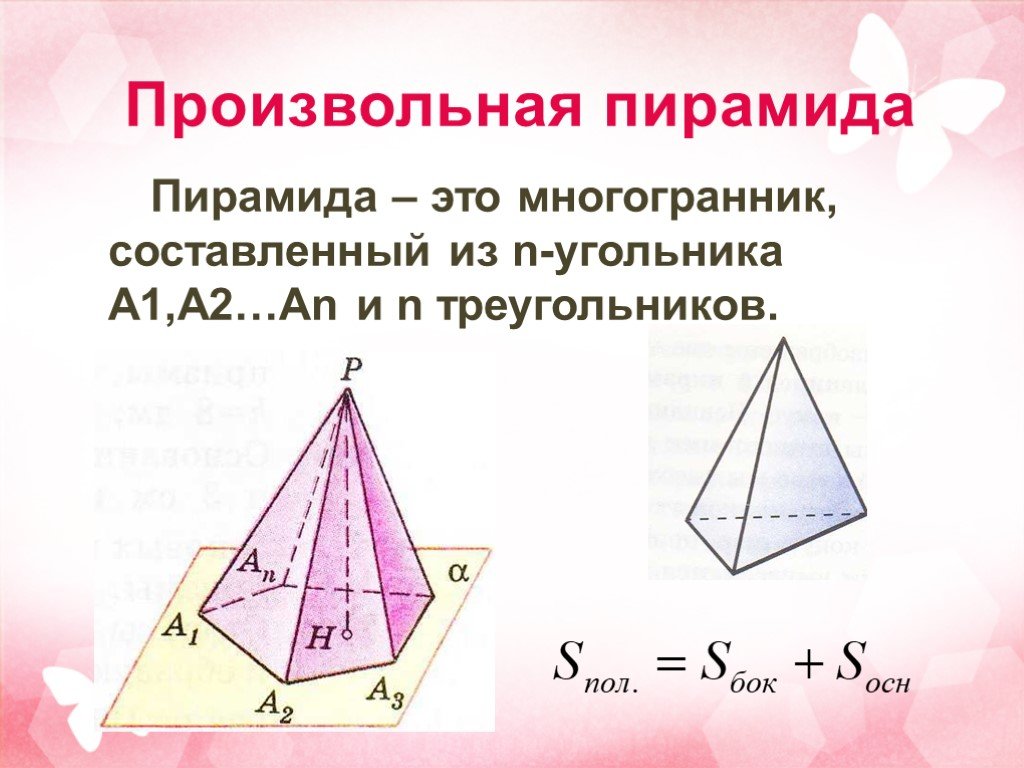
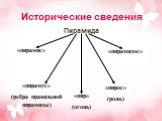
Архитектура и геометрия. . . . . . Многоугольник РА1А2А3….Ап основание пирамиды. Треугольники А1РА2, А2РА3 … боковые грани. Р –вершина пирамиды. РН ...Геометрия и лист бумаги
Если бумага…. Рвется Режется Сгибается Горит Стоит,. то может ли это свойство применяться в геометрии? Результаты опроса. Какие действия с бумагой ...Конспекты
Геометрия треугольника
Тема урока:. . «Геометрия треугольника». Тип урока: обобщающий урок по курсу геометрии. . Форма проведения урока: урок - бенефис». Цель урока:. ...Геометрия окружности
Урок математики в 9 классе. учителя МОУ «СОШ № 20» г. Энгельса. Милюткиной Людмилы Николаевны. и учителя математики МОУ «СОШ № 21» г. Энгельса. ...Геометрия вокруг нас…
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа № 18. Кировский район городской округ город Уфа. . ...Геометрия вокруг нас
Разработала: Ильенко Анжела Владиславовна. Учитель начальных классов МБОУ СОШ №2 г. Стрежевого Томской области. Занятие для учеников 4х кл. по теме ...Геометрия в природе
Класс. : 8. Тема. «Геометрия в природе. ». Тип урока. : урок творческого развития. Цели:. Общеобразовательные:. 1. Систематизировать знаний ...Геометрия в ГИА
Сигайло Елена Валерьевна, учитель математики. МБОУ. . «Средняя общеобразовательная школа пос. Октябрьский». . пос. Октябрьский Лысогорского района ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:20 сентября 2018
Категория:Математика
Содержит:42 слайд(ов)
Поделись с друзьями:
Скачать презентацию