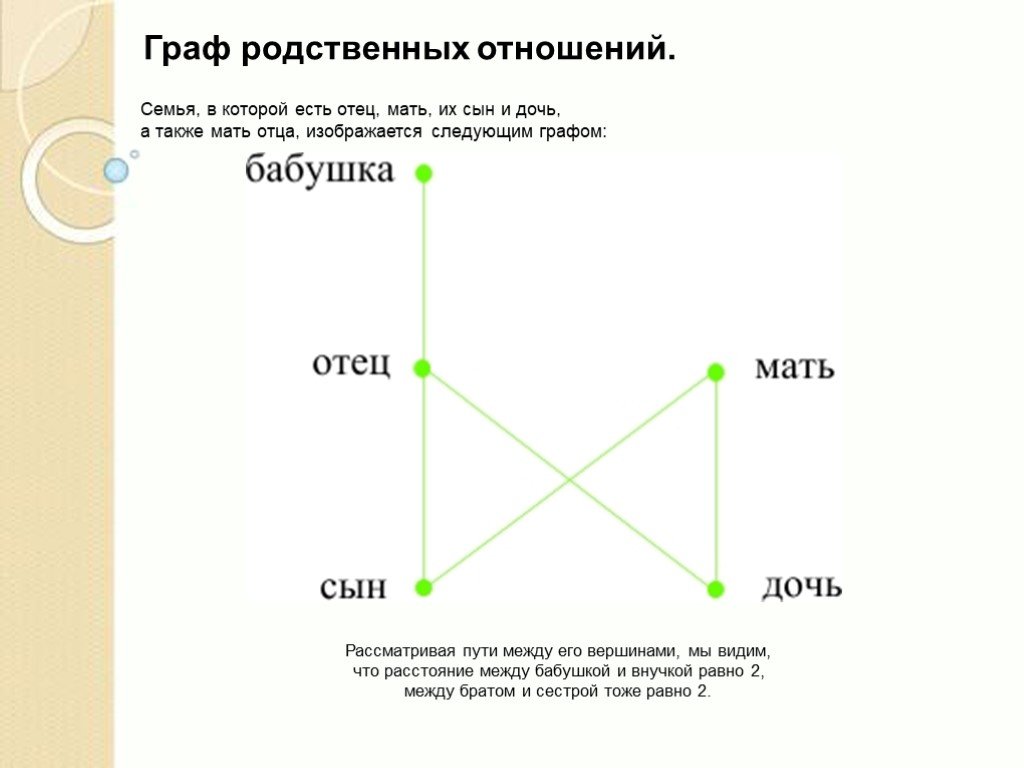
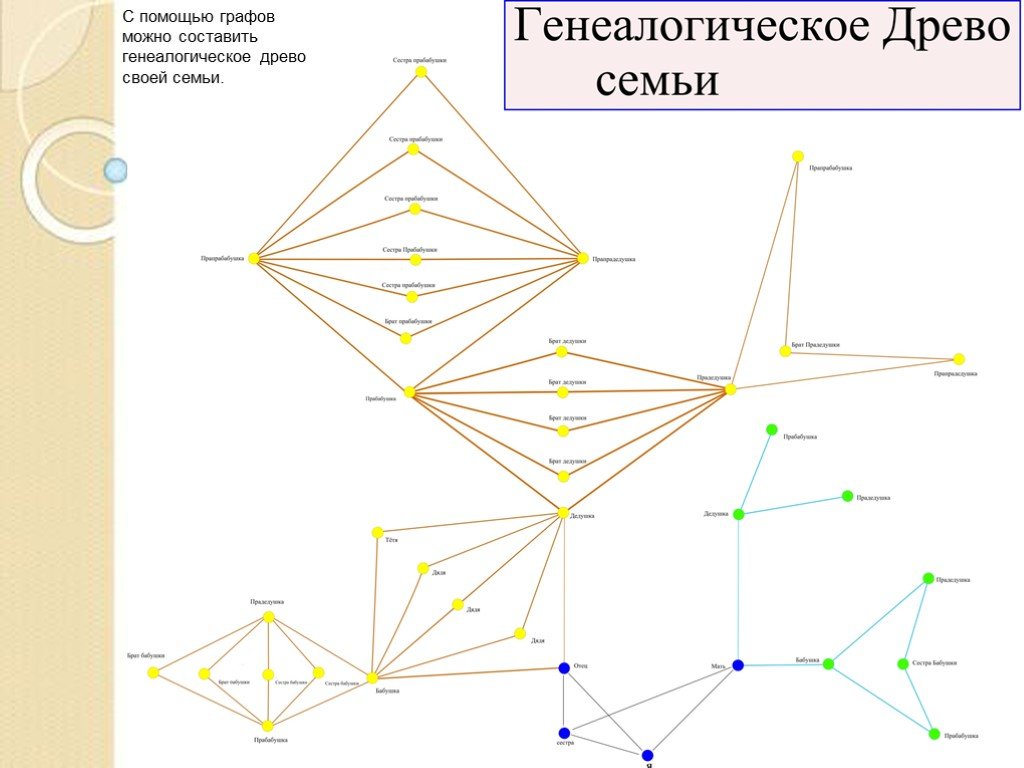
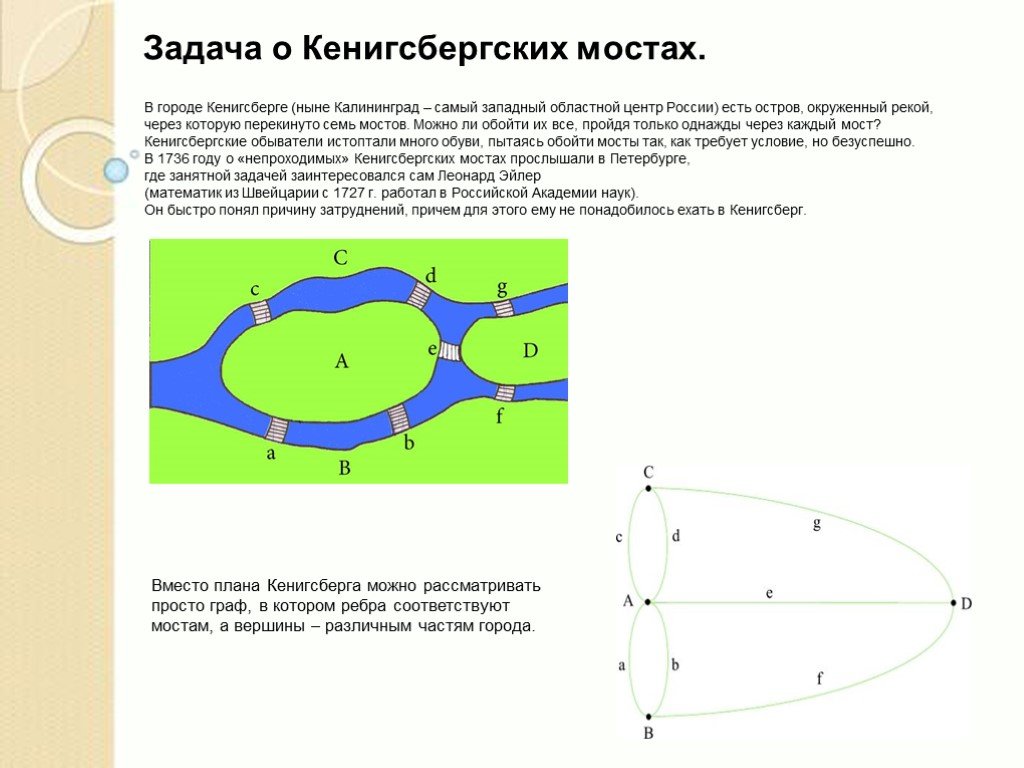
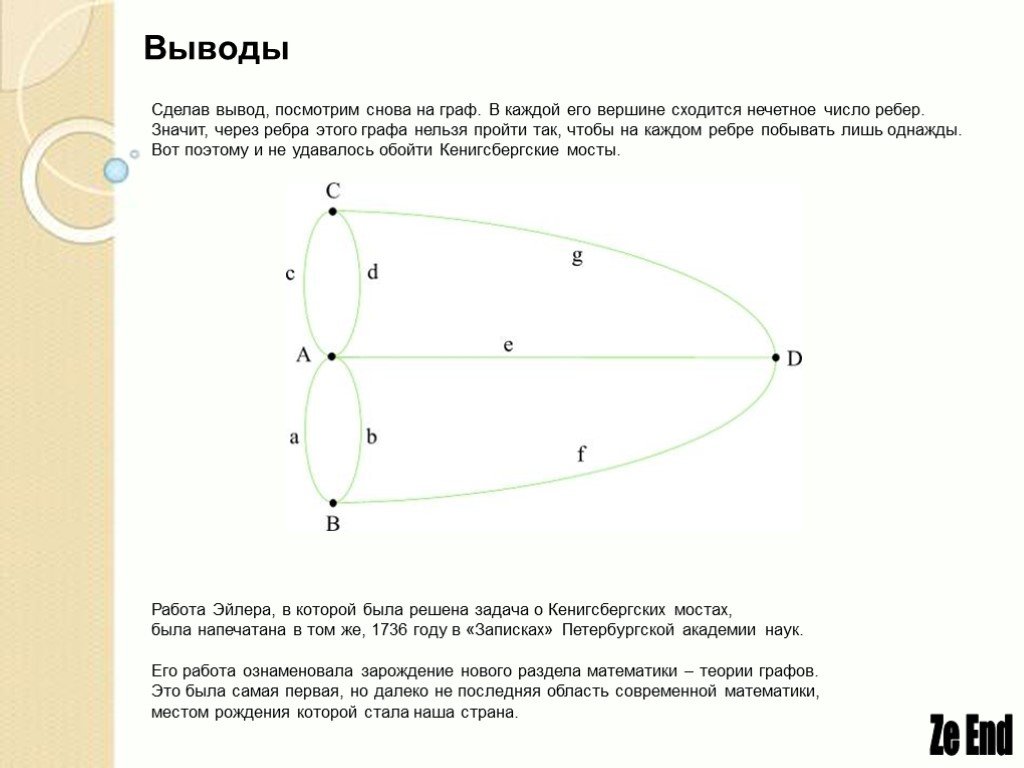
Презентация "Как измерить расстояние между родственниками" по математике – проект, доклад
Презентацию на тему "Как измерить расстояние между родственниками" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 10 слайд(ов).
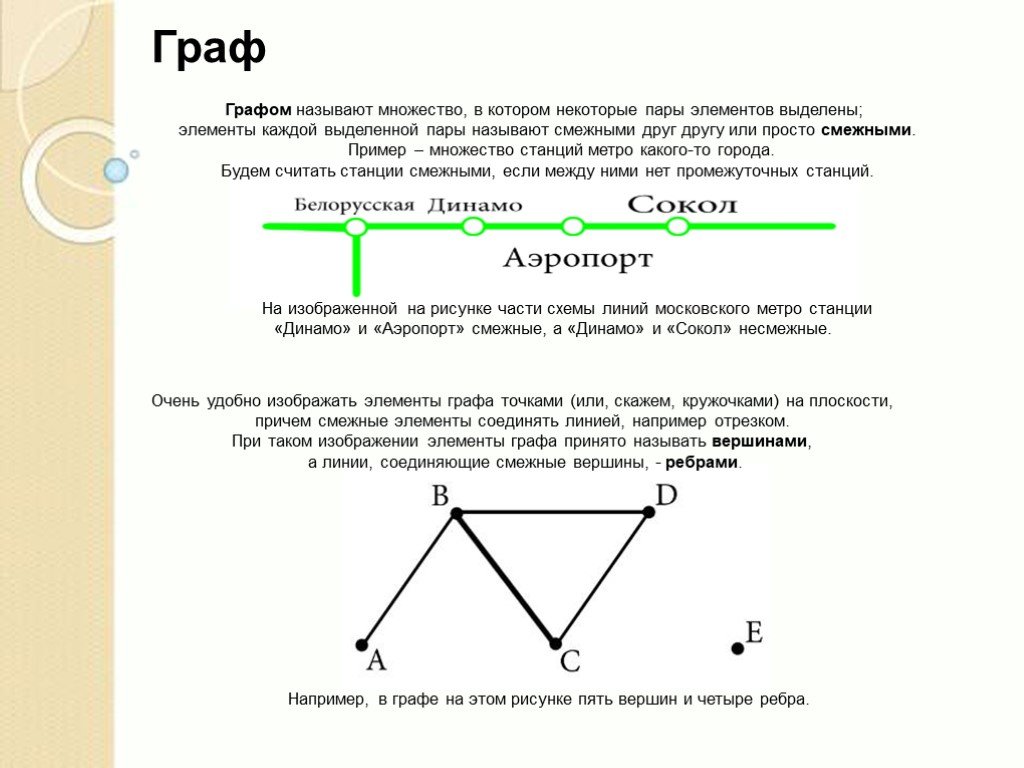
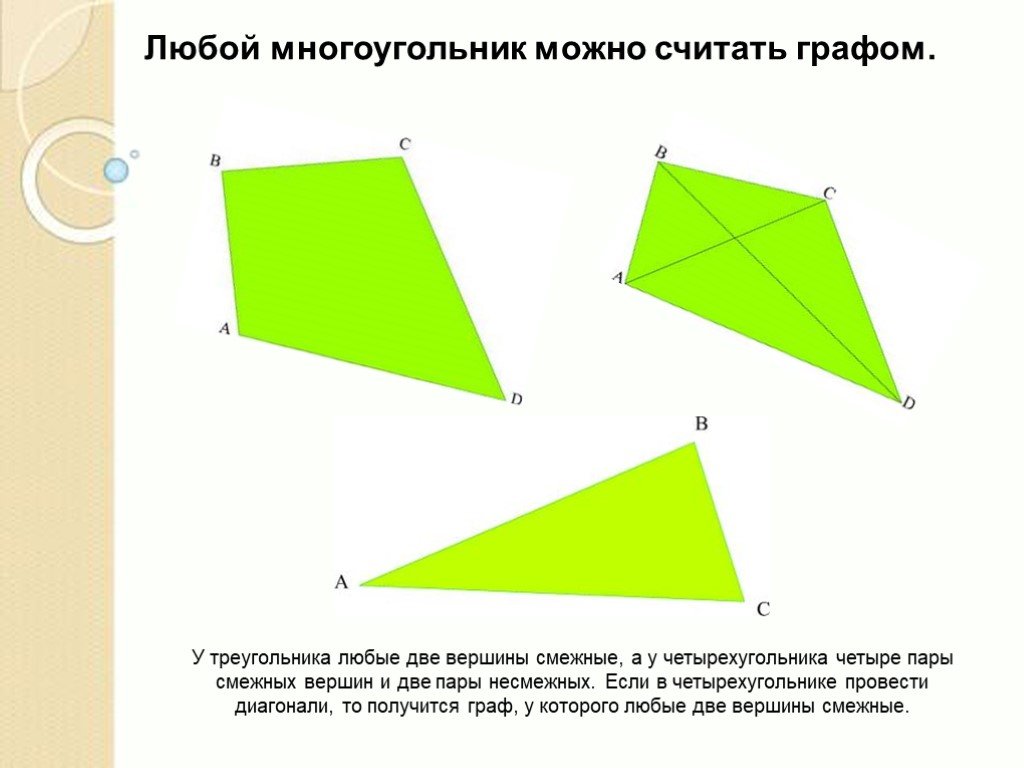
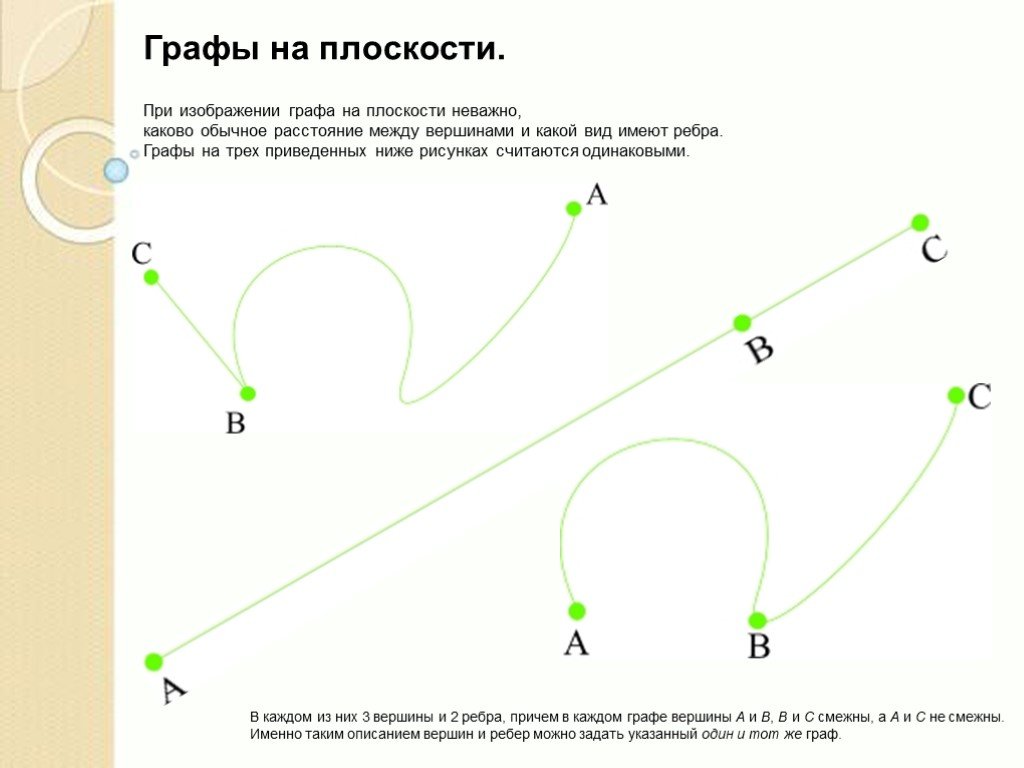
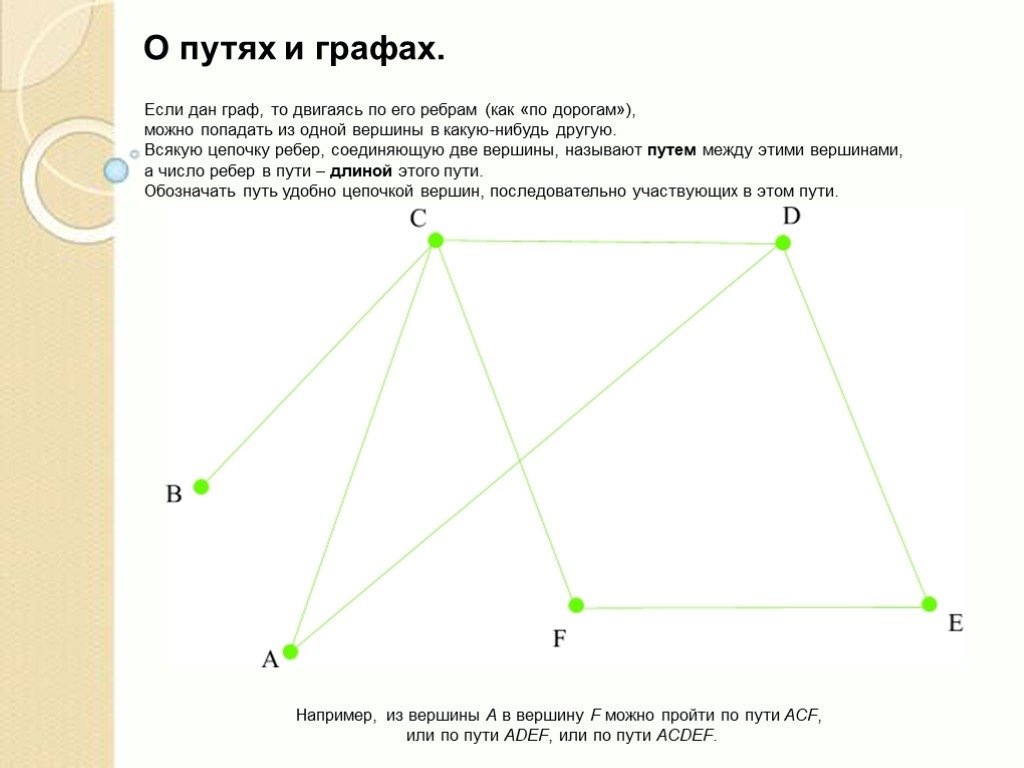
Слайды презентации
Список похожих презентаций
Расстояние между точками
Самостоятельная работа. А(1; 0) С(3; 2) D(2; -1) В(2; 3) О(а; в). А(3; -1); В(-2; 4); С(1; 0); D(0; -2). Найти координаты середины отрезка АВ, АС, ...Скорость, расстояние, время и таинственные отношения между ними
Ход урока:. Устные упражнения. Работа по теме урока. Итог урока. Домашнее задание. S – расстояние t – время v - скорость. S = v * t v = S : t t = ...Расстояние между скрещивающимися прямыми
Материал, полученный и собранный в ходе работы над проектом, является незаменимым при подготовке к решению задач ЕГЭ С2. Умение решать задачи на нахождение ...Расстояние между скрещивающимися прямыми
Основные понятия. Расстоянием между скрещивающимися прямыми называется длина общего перпендикуляра к данным прямым Расстоянием между скрещивающимися ...Взаимосвязь между скоростью, временем, расстоянием
Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении ...Расстояние между точками
Сфера и шар. Координаты точек сферы с центром в точке A0(x0,y0,z0) и радиусом R удовлетворяют равенству. (x-x0)2 + (y-y0)2 + (z-z0)2 = R2. Координаты ...Угол между прямыми в пространстве
В кубе A…D1 найдите угол между прямыми: A1C1 и B1D1. Ответ: 90o. В кубе A…D1 найдите угол между прямыми: AA1 и BC. В кубе A…D1 найдите угол между ...Как готовиться к ГИА-9 по математике
. Содержание работы. Всего в работе 26 заданий, из которых 20 заданий базового уровня (часть I) и 6 заданий повышенного уровня (часть II). Работа ...Соотношения между сторонами угла прямоугольного треугольника
─ Ввести понятие синуса, косинуса, тангенса, котангенса, секанса, косеканса острого угла прямоугольного треугольника. ─Научиться решать прямоугольные ...Угол между прямой и плоскостью
Перпендикулярны ли прямые а и в? Ответ обоснуйте. А В С D F b a. ABCD- прямоугольник, FB┴(ABC). ABCD- параллелограмм, FB┴(ABC). C B O ABCD- ромб, ...Зависимость между синусом, косинусом и тангенсом одного и того же угла
∙. . . П р о в е р ь и о ц е н и с е б я ! Ордината Абсцисса. О с н о в н о е т р и г о н о м е т р и ч е с к о е т о ж д е с т в о :. a2-b2=(a-b) ...Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Вопросы для повторения:. Пропорциональные отрезки: 1. Высота, проведённая из вершины прямого угла на гипотенузу в прямоугольном треугольнике, делит ...Модель отношения между понятиями
Модель отношения между понятиями. Описание природного явления или любого другого объекта в виде текста – это текстовая модель. Изображение объекта ...Перпендикуляр и наклонные. Угол между прямой и плоскостью
Перпендикуляр. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку ...Как выполняли арифметические действия в Древнем Риме?
узнать как выполнялись арифметические действия в Древнем Риме. Цель:. Актуальность: Я считаю необходимым проведение этого исследования, так как: Я ...Как узнать «куда дует ветер» на координатной плоскости?
Вопросы учебной темы: Квадратичная функция и ее график. Функция обратная пропорциональность и ее график. Линейная функция и ее график. Функция квадратного ...Как возникли цифры?
Цель работы:. Выяснить, когда и как возникли цифры, распознать различные системы счета. В древние времена, когда человек хотел показать сколькими ...Как возникли дроби?
«Историки». ПРЕДСТАВЛЯЮТ!!!!! «Как возникли дроби». В каких источниках впервые упоминается о дробях:. Египетский математический кожаный свиток Московский ...Как возникли дроби
Роман Корженевский, 5 класс. Слыхали ли Вы о том, как ломают числа? А ведь ломаными числами пользуются и теперь, только называют их иначе. Попробуйте ...Как «устроены» числа. Десятичный состав чисел
10 десять 1 десяток. 1 десяток и 1 10 + 1 = 11 Одиннадцать. 1 десяток и 2 10 + 2= 12 Двенадцать. 1 десяток и 3 10 + 3= 1 3 Тринадцать. 14. 15. 16. ...Конспекты
Взаимосвязь между скоростью, временем и расстоянием
Урок математики в 4 классе. Тема. Взаимосвязь между скоростью, временем и расстоянием. Вид урока:. закрепление полученных знаний. . . . ...Взаимосвязь между скоростью, временем и расстоянием
Конспект урока по теме: «Взаимосвязь между скоростью, временем и расстоянием». Цель деятельности учителя:. способствовать развитию умений составлять ...Угол и расстояние между скрещивающимися прямыми
Урок геометрии. . "Угол и расстояние между скрещивающимися прямыми". . . Учитель: Федорова Е.В., МОУ «СОШ № 77», г.Саратов. . Учебный план ...Взаимосвязи между скоростью, временем и расстоянием
Муниципальное бюджетное общеобразовательное учреждение. «Пришибинская основная общеобразовательная школа». . Конспект урока по математике ...Как сравнить углы. Как измерить углы
Конспект урока математики с применением ИКТ по теме «Как сравнить углы. Как измерить углы», проведённого в 3 классе. Цель:. Создать условия для ...Связь между величинами: скорость, время, расстояние
Тема: "Связь между величинами: скорость, время, расстояние". . . Цели: продолжить работу по формированию решения задач на движение; отрабатывать ...Скорость, время, расстояние
Урок математики 3 класс. Программа «Школа 2100». Тема урока:. Скорость, время, расстояние. Тип урока:. «открытие» новых знаний . Задачи урока:. ...Соотношение между единицами площади
Дата_______________. Тема: Соотношение между единицами площади. Цель: Познакомить учащихся с соотношением между единицами площади. Развивать ...Связь между суммой и слагаемыми
Рачкова Мария Владимировна. учитель начальных классов. ГБОУ СОШНО № 196 г. Москвы. ...Скорость, время, расстояние
Предмет: Математика. Класс: 3. Тема: Скорость, время, расстояние. Этапы урока. Ход урока. . Примечание. . . 1. Орг. Момент. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 июля 2019
Категория:Математика
Содержит:10 слайд(ов)
Поделись с друзьями:
Скачать презентацию