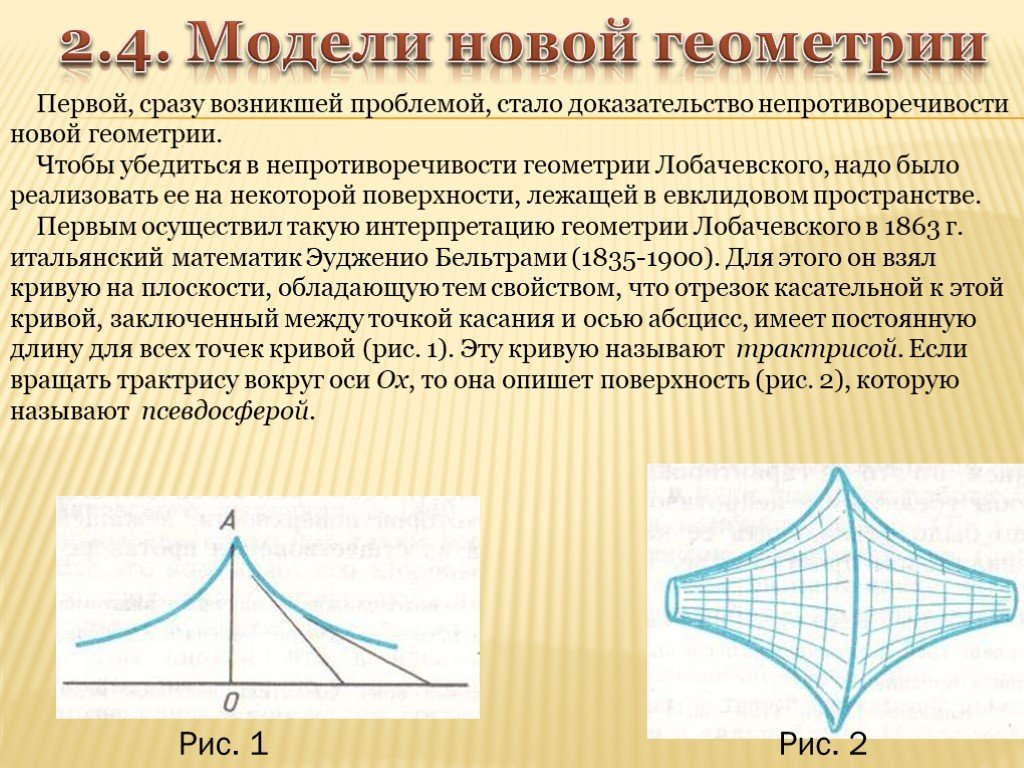
Презентация "Развитие геометрических знаний от Евклида до Лобачевского" по математике – проект, доклад
Презентацию на тему "Развитие геометрических знаний от Евклида до Лобачевского" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
Слайды презентации
Список похожих презентаций
Геометрия Евклида и геометрия Лобачевского. Сходства и отличия
Евклидова геометрия. Евкли́д или Эвкли́д (, ок. 300 г. до н. э.) — древнегреческий математик. Мировую известность приобрёл благодаря сочинению по ...Зависимость расстояния между точками пересечения прямой и окружности и расстояния от центра окружности до этой прямой
Цель:. Определение зависимости расстояния между точками пересечения прямой и окружности и расстояния от центра окружности до прямой. Задачи:. Рассмотреть ...Геометрия до Евклида в очерках и задачах
Введение:. Цель моей работы: Изучение исторических сведений, показать связь основных этапов развития математики с этапами развития человечества. Задачи ...Биографии великих математиков (от сотворения мира до наших дней)
Фалес Милетский (ок. 625–547 гг. до н.э.). Греческий купец, живший в Милете, греческом полисе (городе-государстве на западном побережье Малой Азии; ...Геометрия Н.И. Лобачевского
Оглавление. 1) Цели. 2)Задачи. 3)Содержание: 3.1 Биография Лобачевского. 3.2 Эксперимент. 3.3 Изучение постулата Евклида и аксиомы Лобачевского. 3.4 ...Геометрия Лобачевского
Проблема V постулата. Система аксиом современных школьных учебников геометрии базируется на системе аксиом Евклида. Евклидова геометрия на протяжении ...Геометрия Лобачевского
Сотни профессиональных геометров разных времён и народов, тысячи любителей математики в течение 20-х веков искали доказательство пятого постулата. ...Геометрия Лобачевского
Цель урока. Познакомить учащихся с неевклидовой геометрией , ее создателями, некоторыми теоремами геометрии Лобачевского. Расширение представлений ..."Умножение дробей, нахождение дроби от числа"
. Выполнить умножение: 3 8 ∙2=. Выполнить умножение: 3 7 ∙ 2 9 =. 2 21. Выполнить умножение: 5∙1 7 15 =. 7 1 3. Вычислить площадь квадрата со стороной ...Задачи на нахождение процента от числа
Задача. Семья из пяти человек съедает около 10 кг пищи в день. 75% рациона составляют супы, макароны и картофель (в любом виде). 15% рациона составляет ...Выделение элементов и свойств геометрических фигур
Геометрические фигуры являются эталонами, пользуясь которыми человек определяет форму предметов и их частей. Проблему знакомства детей с геометрическими ...Архимед (287 – 212 до н.э.)
Вдруг искупаться я решил И ванну полную налил, Я сел в неё и вот беда, Из ванны вылилась вода. Пришла идея мне тогда, И “Эврика! – воскликнул я”. ...V postulatum Евклида
Проект подготовили: ученики 10 класса «А» Косинов Никита Ушакова Екатерина Мурзакова Алина Кузьмина Юлия. МОУ многопрофильный лицей № 20. Ульяновск ...«Начала» Евклида
Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Но теория многогранников является и современным ...«Действия с дробями», «Нахождение дроби и процентов от числа»
Систематизация знаний по темам: «Действия с дробями», «Нахождение дроби и процентов от числа», Отработка практических навыков выполнения действий ...ГИА-2012. Решение планиметрических задач на нахождение углов геометрических фигур
1 3 4 5 6 7 8 9 10 11. Вашему вниманию представлено двенадцать прототипов задачи № 11 Открытого банка заданий по математике. ГИА – 2012. Два острых ...Динамические модели геометрических фигур
Грамота, уроки 65-66. Математика, уроки 14, 15. Математика, уроки 26, 27. Математика, уроки 28, 29. Математика, уроки 40, 41. Математика, уроки 46, ...Геометрия Евклида
Древнегреческий математик. Родина - Афины Ученик Платона Научная деятельность протекала в Александрии (3 в. до н. э.), и ее расцвет приходится на ...Загадки от Всезнайки
1 4 5 3 Реши пример. 6 7. 2. 8. Какие из этих насекомых могут только ползать? Найди тень. . . ...Геометрия Лобачевского
Гипотеза. Многие математики, жившие после Евклида, пытались доказать, что эта аксиома (V постулат Евклида) – лишняя, т.е. она может быть доказана ...Конспекты
Закрепление знаний о нумерации чисел от 1 до 10
МАТЕМАТИКА 1 класс. ТЕМА:. Закрепление знаний о нумерации чисел от 1 до 10. ЦЕЛИ:. -закрепление вычислительных умений и навыков в пределах 10;. ...Закрепление знаний нумерации чисел от 1 до 10
Творческий урок-игра. ТЕМА УРОКА: «Закрепление знаний нумерации чисел от 1 до 10». ЦЕЛИ. Повторение изученного материала по теме « Нумерация ...Действия с дробями. Нахождение доли от числа
Открытый урок по математике. 4 «а» класс, учитель Подлабухова Лидия Ивановна. средняя школа № 6 г. Конаково. Тема: Действия с дробями. Нахождение ...Геометрические фигуры. Числа от 1 до 20
ФИО: Тихонова Елена Юрьевна. Предмет: Математика. Класс: 1 класс. Учебная тема: Геометрические фигуры. Числа от 1 до 20. . (Образовательная ...Время от 0 часов до 24 часов
Математика 4 класс. УМК «Школа России». . . Конспект подготовила учитель начальных классов МБОУ «СОШ №33 г.Владимира». Королёва Любовь Петровна. ...Закрепление. Числа от 1до10
Урок. . по математике. . на тему «. Закрепление. Числа от 1 до 10. ». Тема: Закрепление. Числа от 1до10. Цели:. ...Знакомимся с числами от 11 до 20
Тип урока. «Урок открытия нового знания». Тема урока. : «Знакомимся с числами от 11 до 20» (урок № 31). Основное предметное содержание деятельности ...Исследование геометрических моделей (планиметрия)
11 класс. Базовый уровень. OC. Linux. 5.0.2 Школьный мастер или Windows. . Конспект урока. «Исследование геометрических моделей (планиметрия)». ...Закрепление числового ряда от 1 до 5
Конспект по математике в средней группе №5. Тема :«Закрепление числового ряда от 1 до 5». Программные задачи:. Формировать умение ориентироваться ...Запись и чтение чисел от 11 до 20. Сравнение чисел
Математика. 1 класс. Тема:. Запись и чтение чисел от 11 до 20. Сравнение чисел. Цели урока. Учить записывать и читать числа от 11 до 20. . ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:6 декабря 2018
Категория:Математика
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию