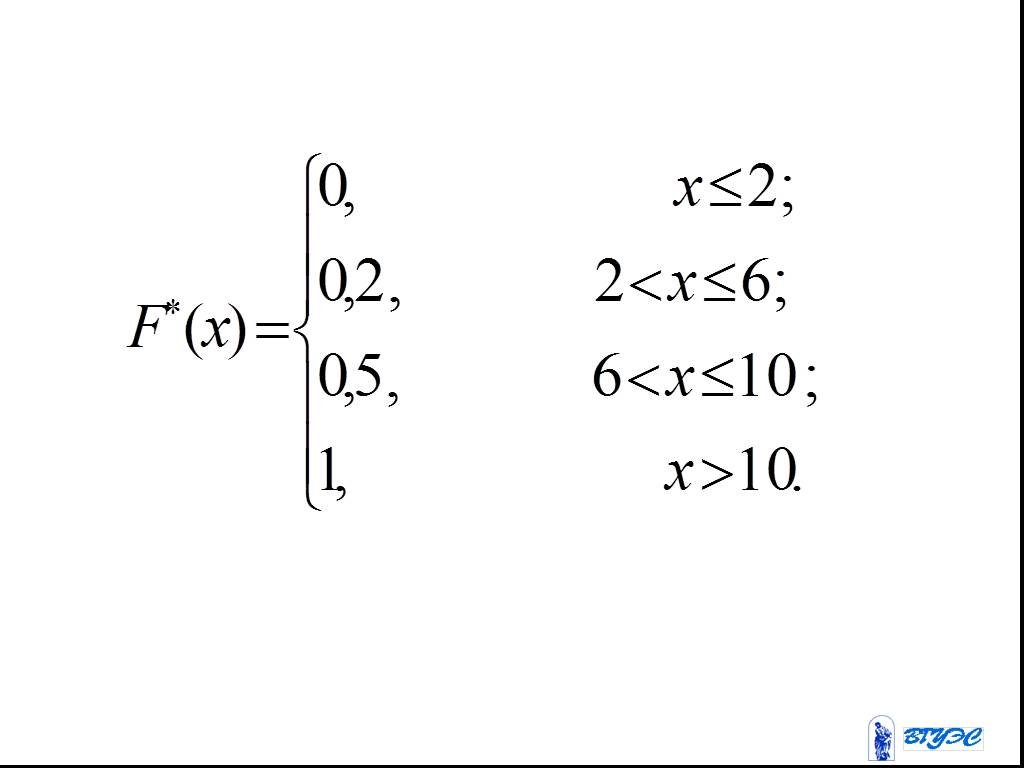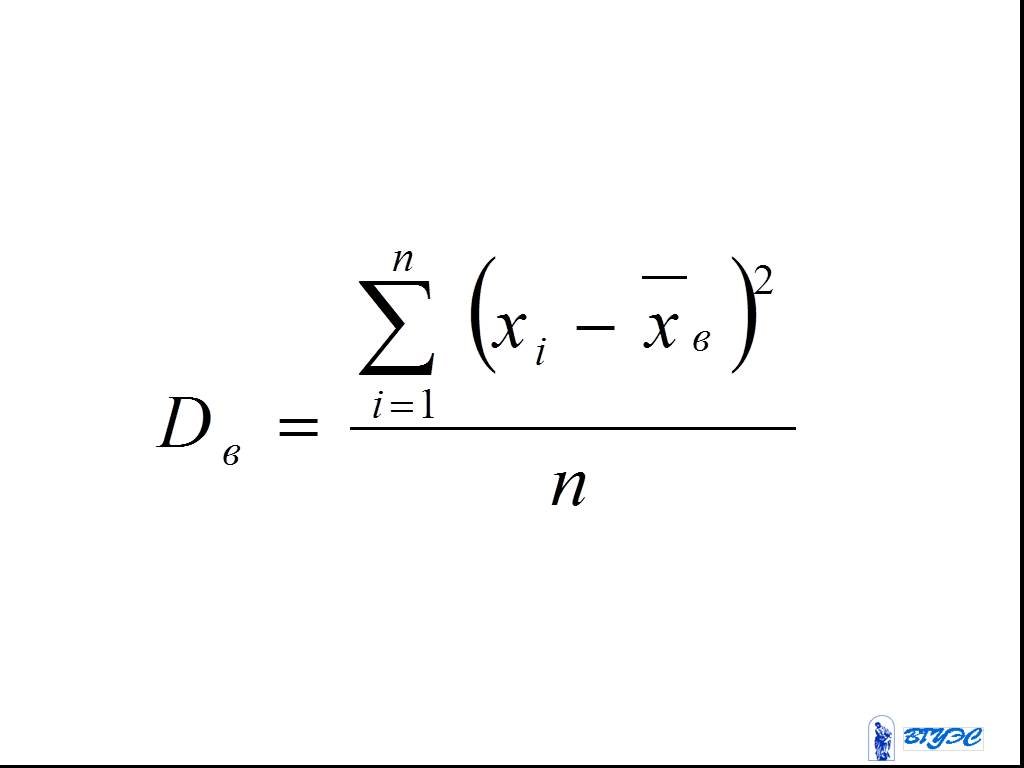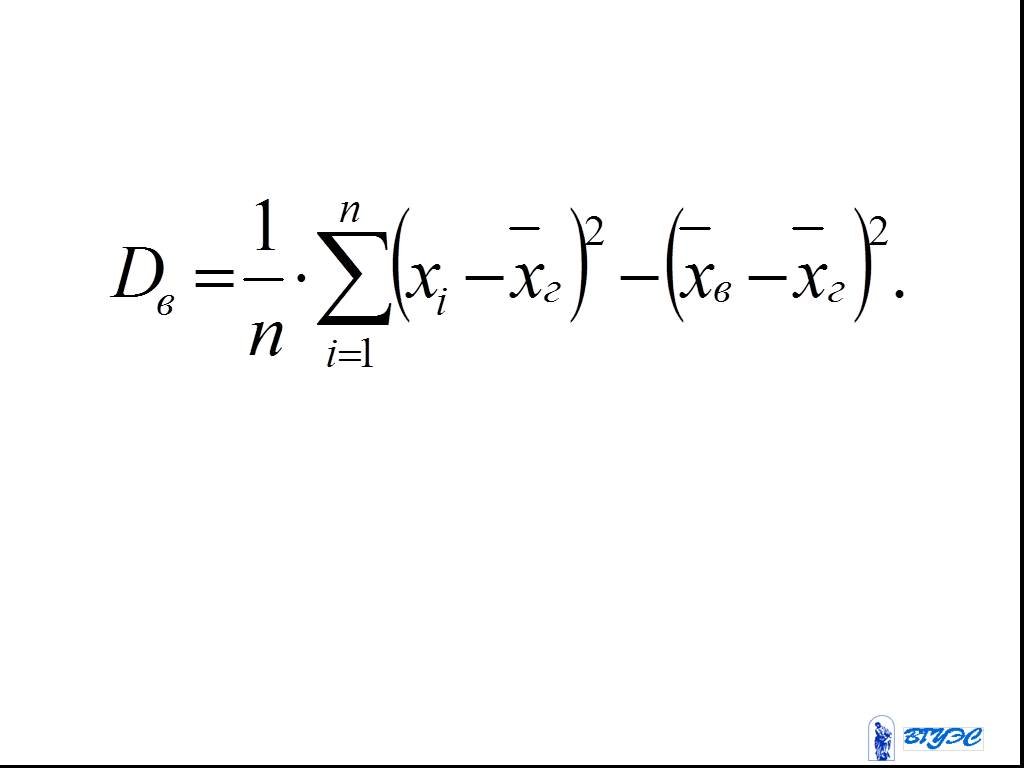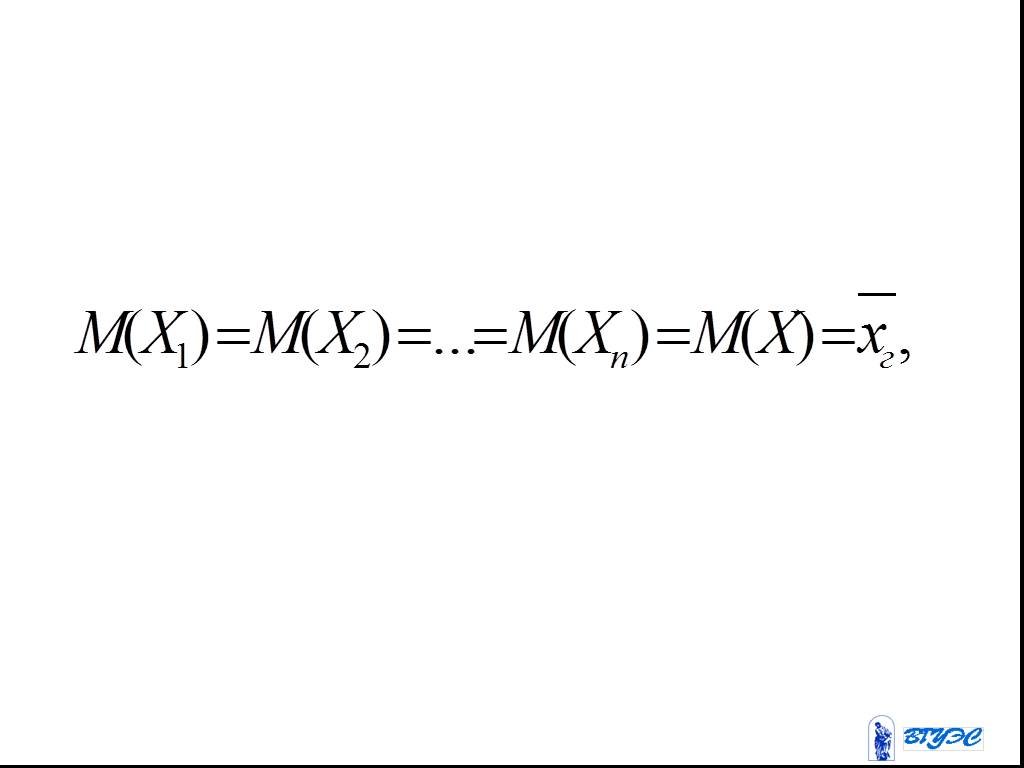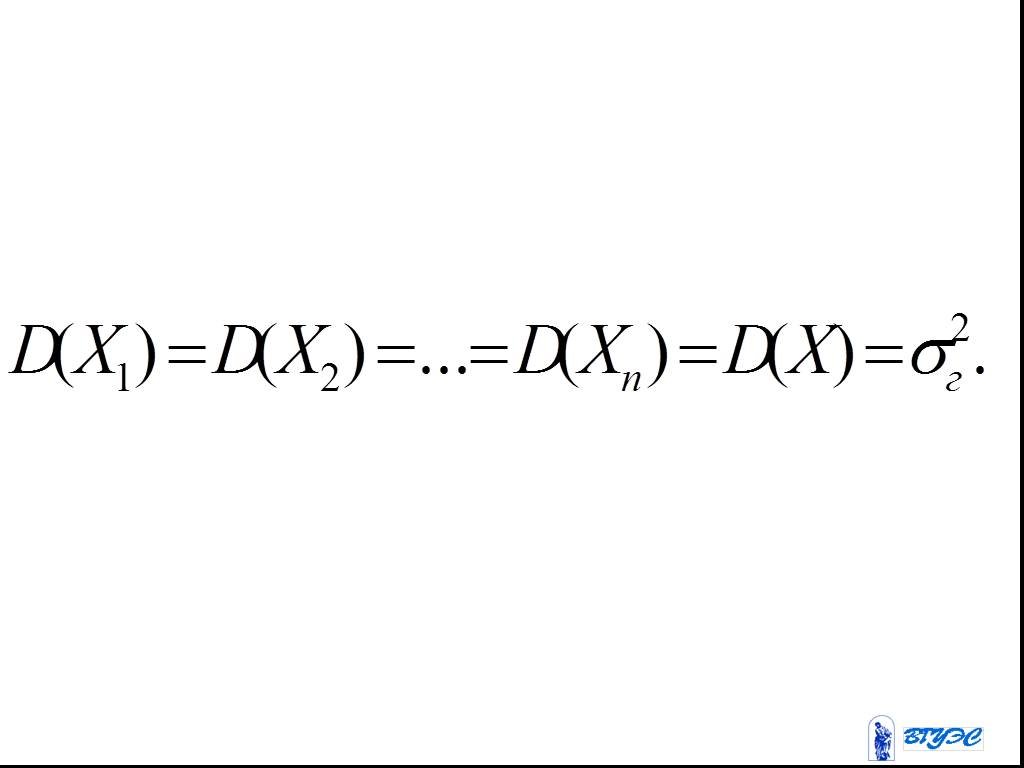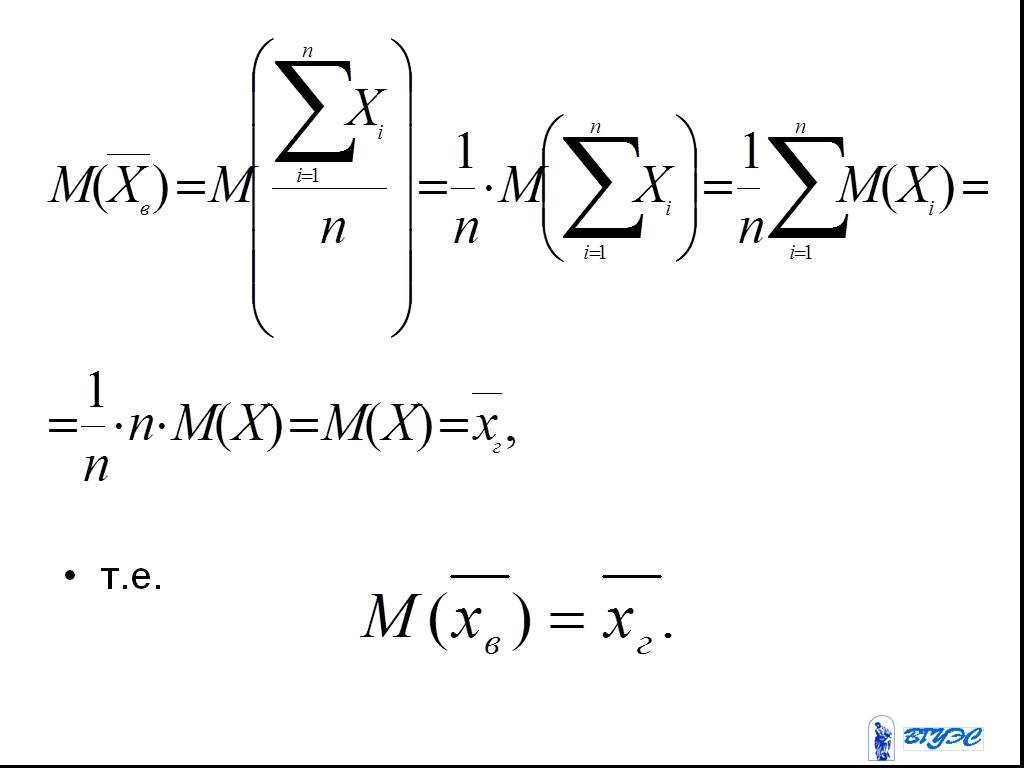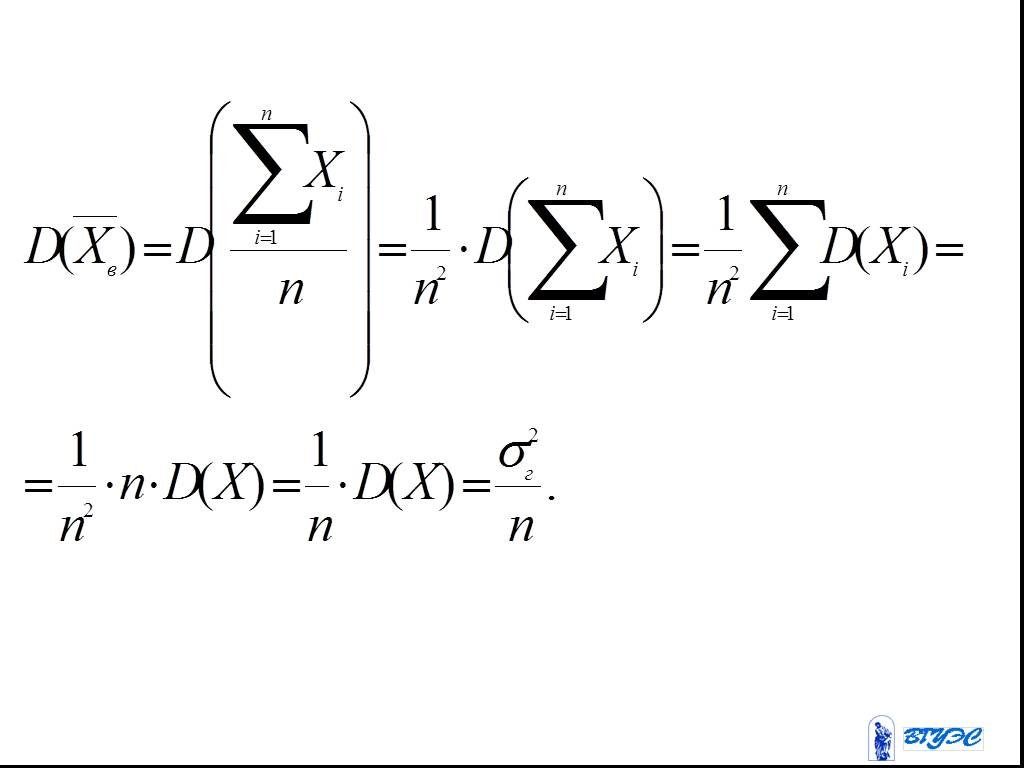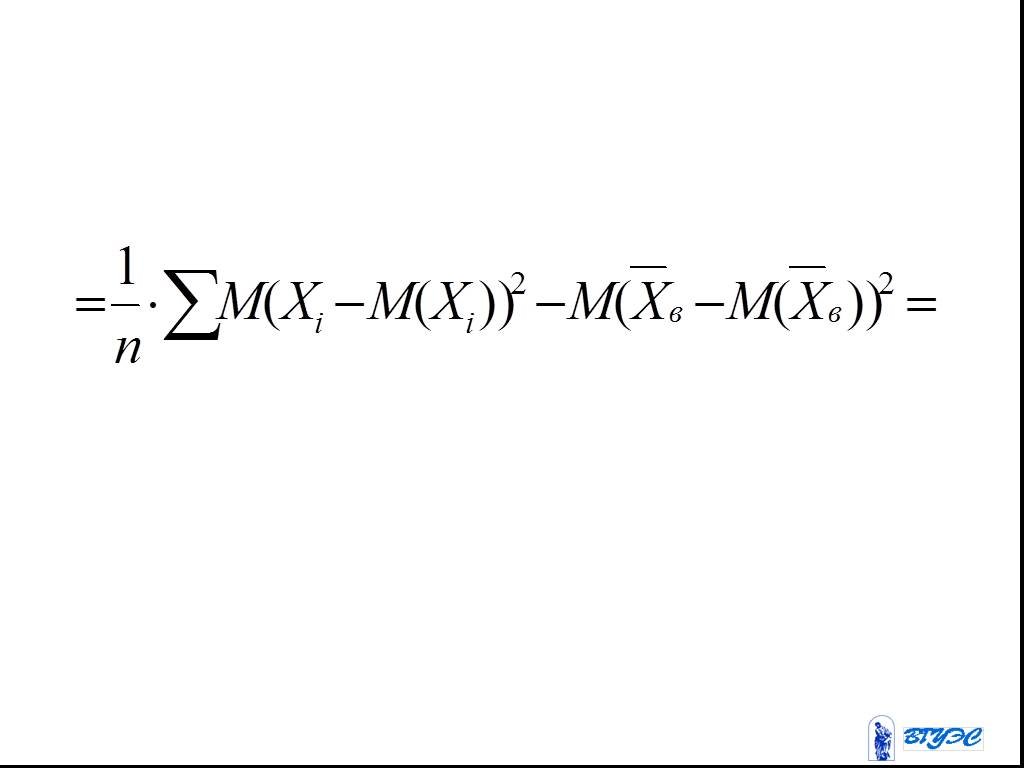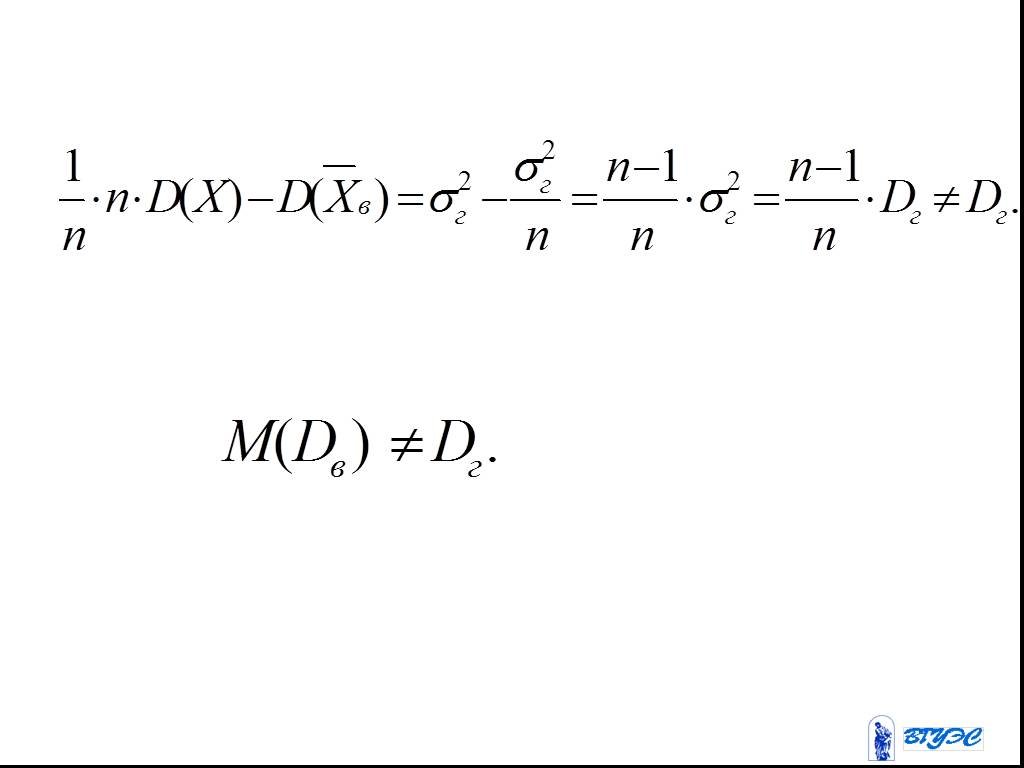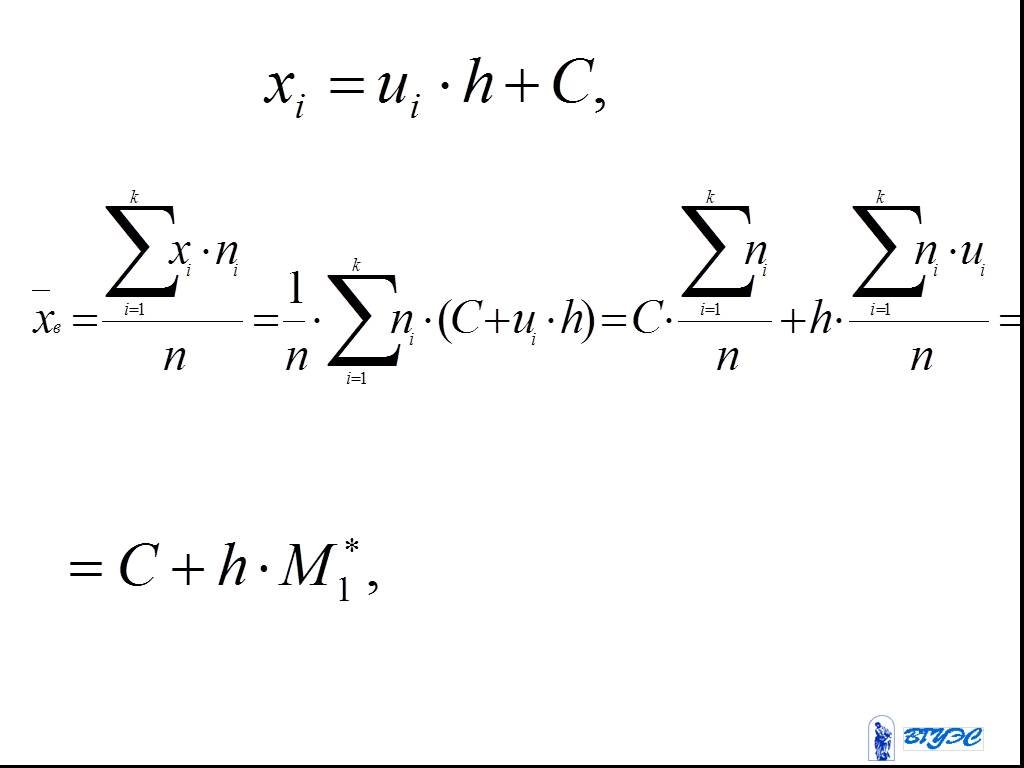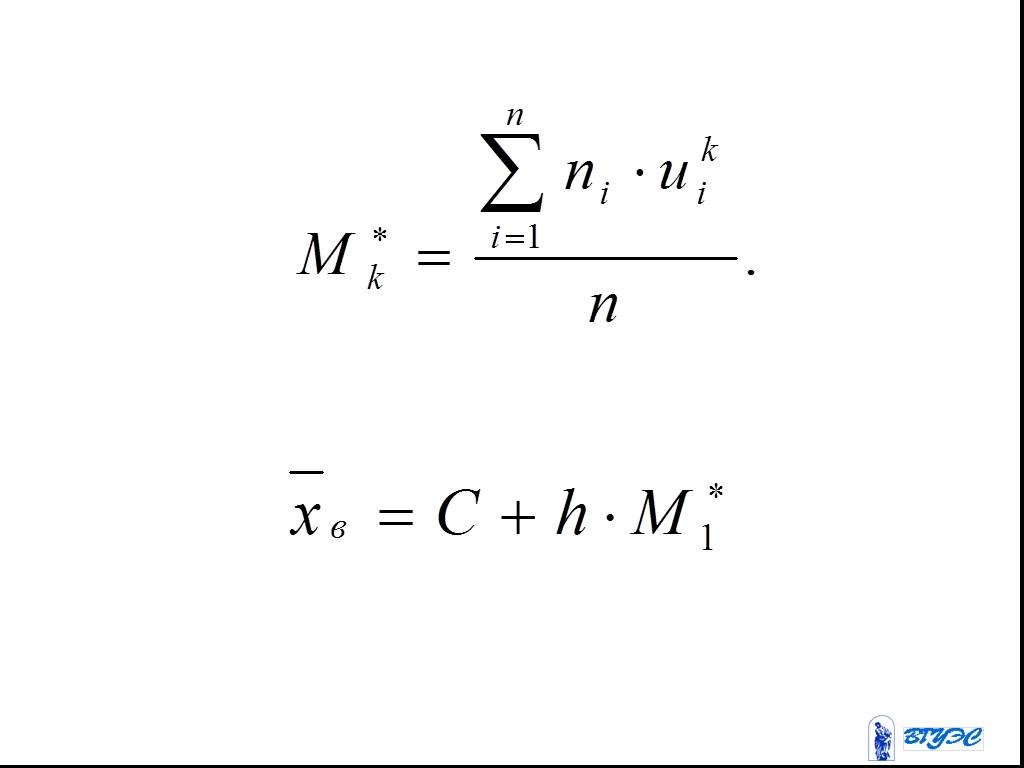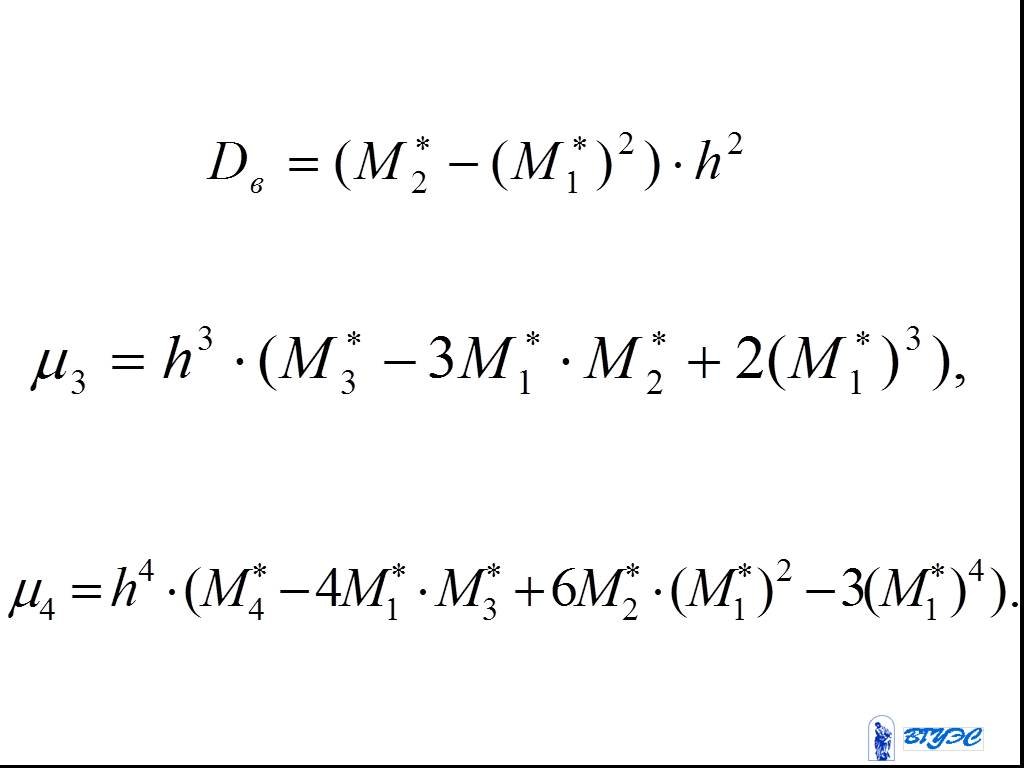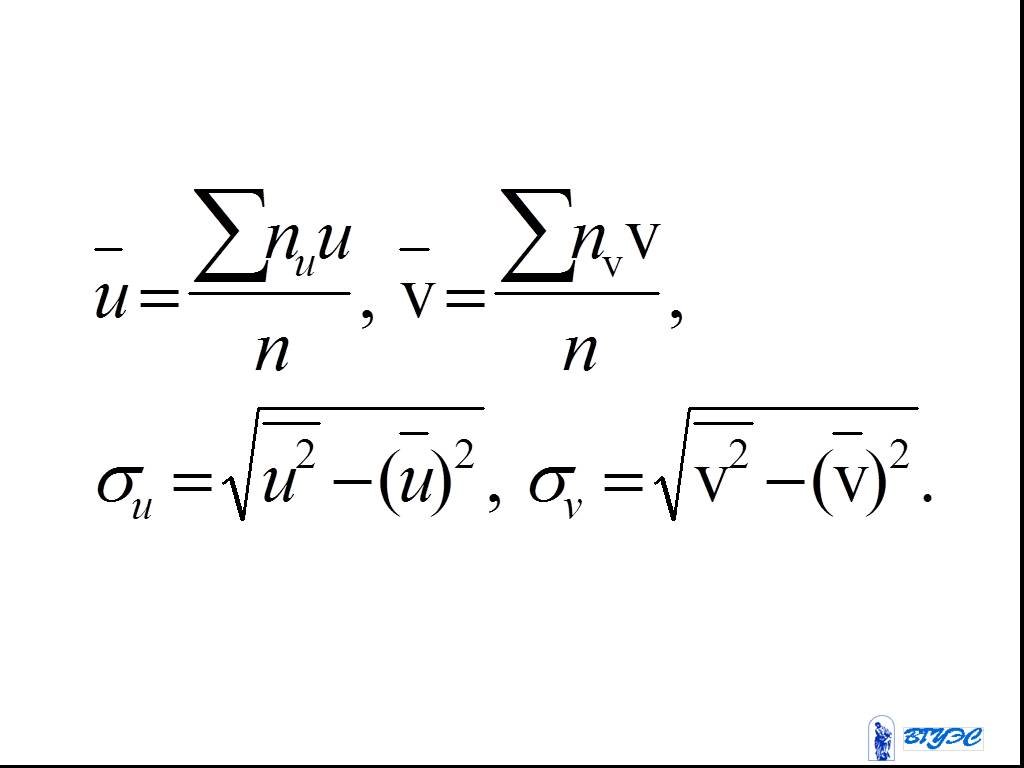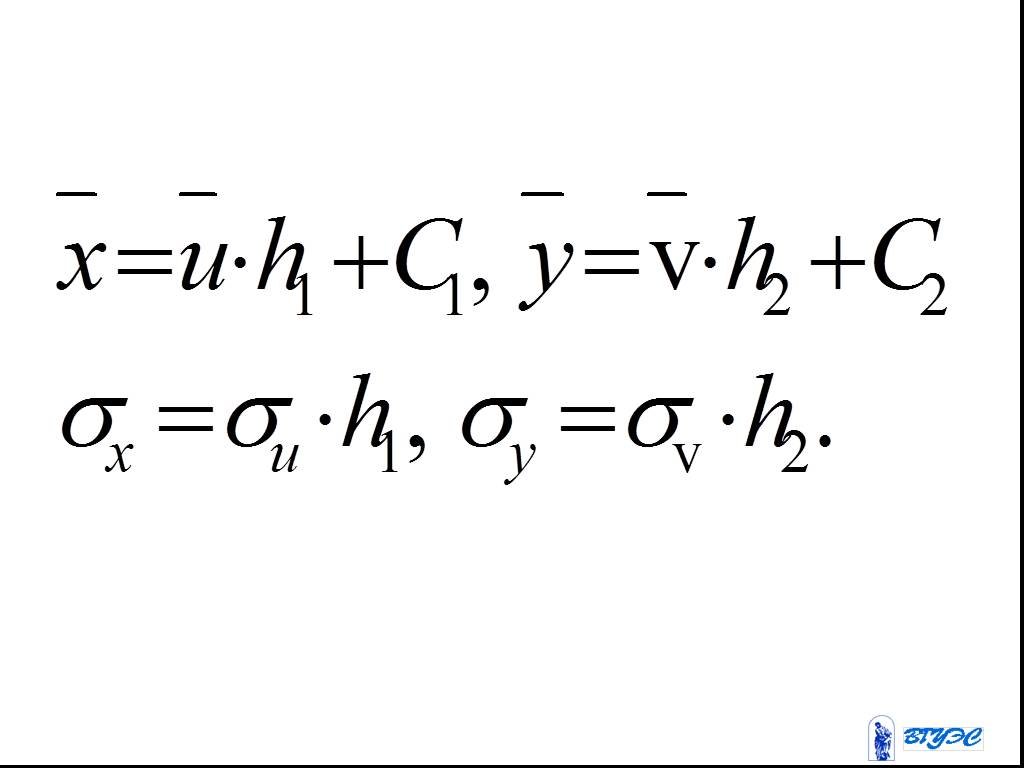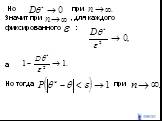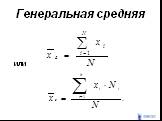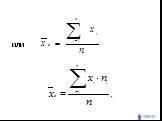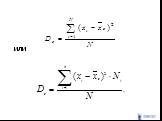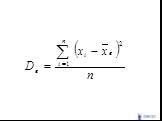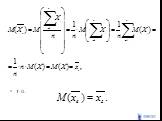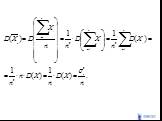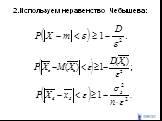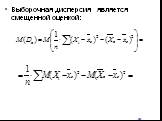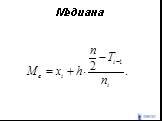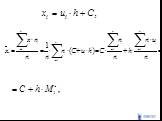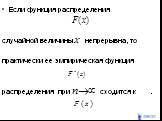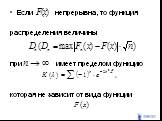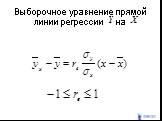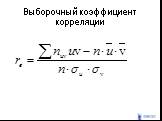Презентация "Математическая статистика" по экономике – проект, доклад

Математическая статистика

Задачи математической статистики

Оценка неизвестной функции распределения. Оценка неизвестных параметров распределения. Статистическая проверка гипотез.

Выборочный метод. Генеральная совокупность. Выборка

Опр. Исследуемая совокупность объектов наз. генеральной совокупностью ( - очень велико, в некоторых случаях количество значений, образующих генеральную совокупность, можно считать и бесконечным).

Опр. Совокупность объектов , отобранных случайным образом из генеральной совокупности наз. выборочной совокупностью (выборкой), где Число наз. объемом выборки.

Метод основанный на том, что по выборочной совокупности выделенной из данной генеральной совокупности делается заключение о всей генеральной совокупности наз. выборочным методом

Виды выборок

Собственно-случайная

Выборка образованная случайным выбором элементов без расчленения на части или группы.

Механическая

Выборка, в которую элементы из генеральной совокупности отбираются через определенный интервал. Например, если объем выборки должен составлять 10% (10%-я выборка), то отбирается каждый 10-й элемент.

Типическая

Выборка, в которую случайным образом отбираются элементы из типических групп, на которые по некоторому признаку разбивается генеральная совокупность.

Серийная

Выборка, в которую случайным образом отбираются не элементы, а целые группы совокупности(серии), а сами серии подвергаются сплошному наблюдению.

Способы образования выборки

Повторный отбор

Каждый элемент, случайно отобранный и обследованный, возвращается в общую совокупность и может быть повторно отобран.

Бесповторный

Отобранный элемент не возвращается в общую совокупность

Статистический ряд. Статистическое распределение. Эмпирическая функция распределения

Варианты: Вариационный ряд: или

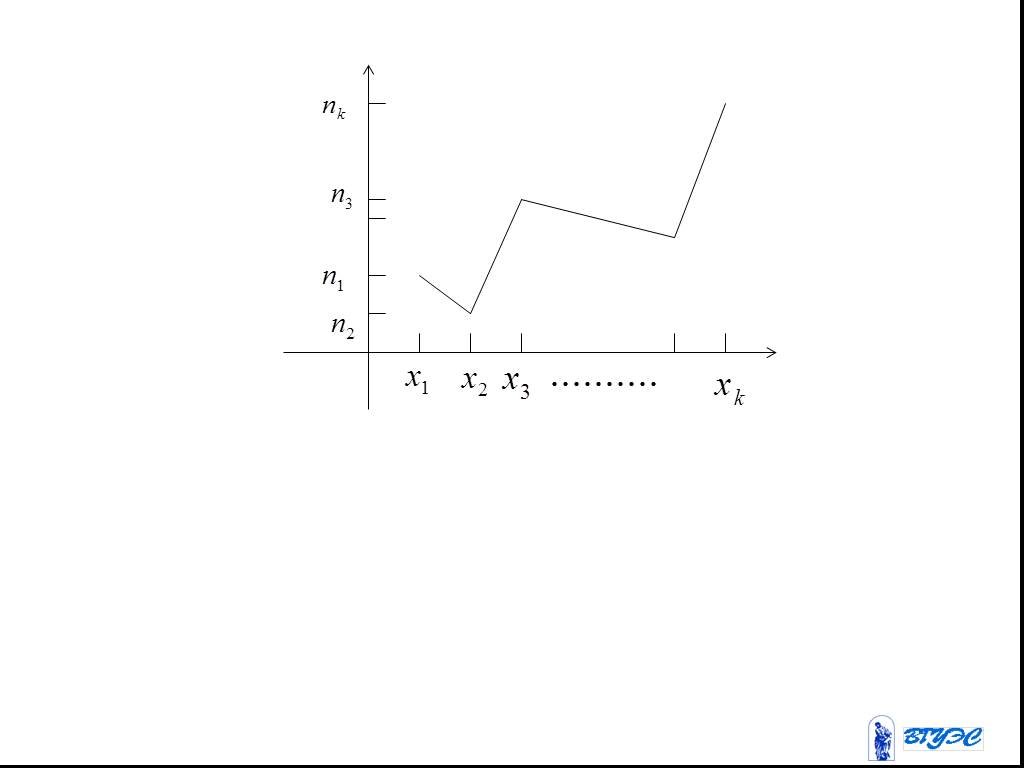
Из генеральной совокупности извлечена выборка объема наблюдалась раз; наблюдалась раза; наблюдалась раза; ………………………………… наблюдалась раз. Причем .

Числа называются частотами. Числа , где наз. относительными частотами.

Статистическое распределение выборки

Полигон частот

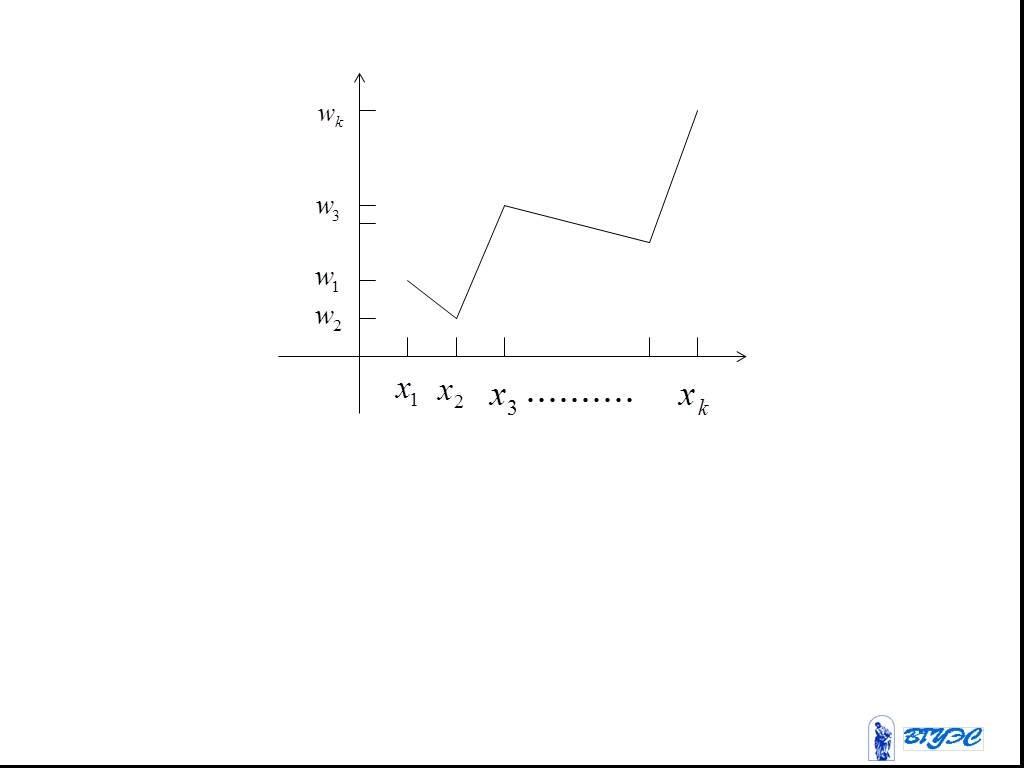
Полигон относительных частот

Эмпирическая функция распределения

Эмпирическая функция распределения это функция равная отношению числа вариант, меньших , к объему выборки: .

Свойства эмпирической функции распределения

1) 2) - неубывающая; 3) если наименьшая варианта, то при 4) если наибольшая варианта, то при

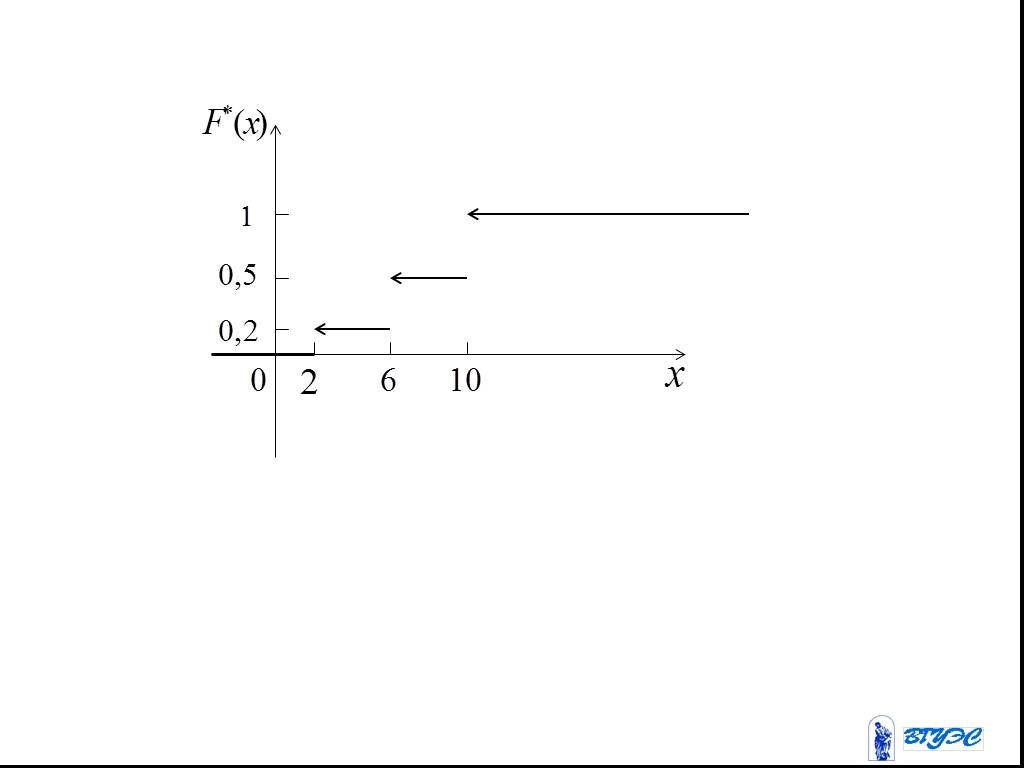
Пример. По данному распределению выборки построить эмпирическую функцию.

Статистическая совокупность

Число интервалов определяется по формуле Стерджеса

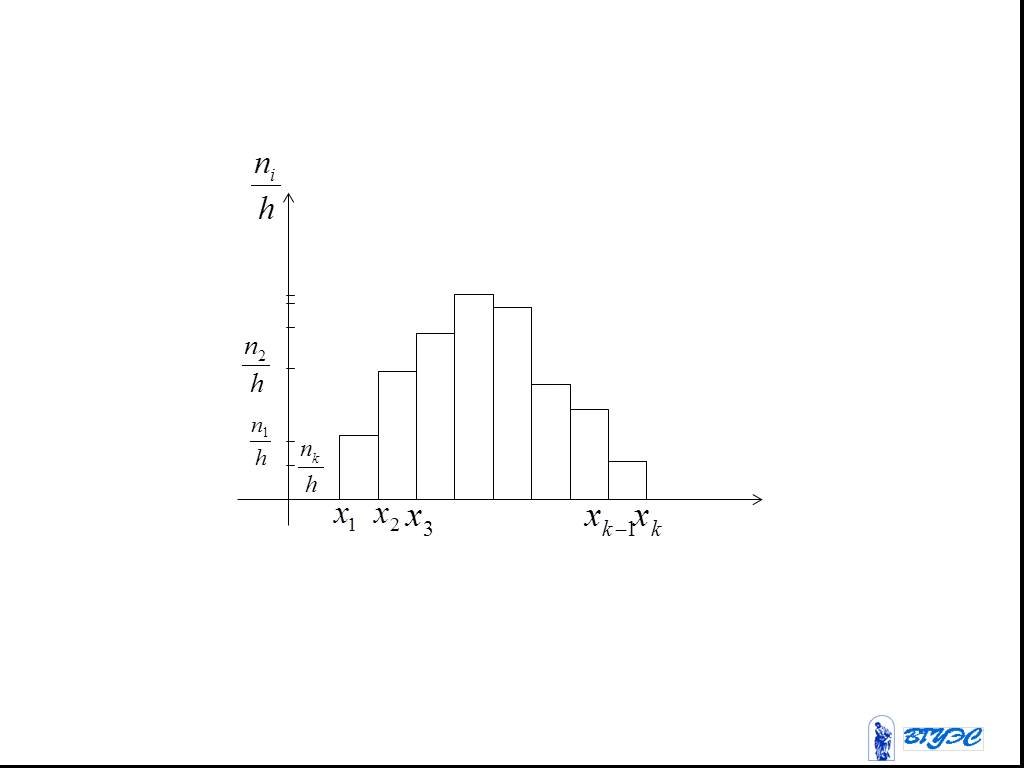
Гистограмма частот

Ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиною , а высоты равны отношению (плотность частот).

Площадь гистограммы частот тогда

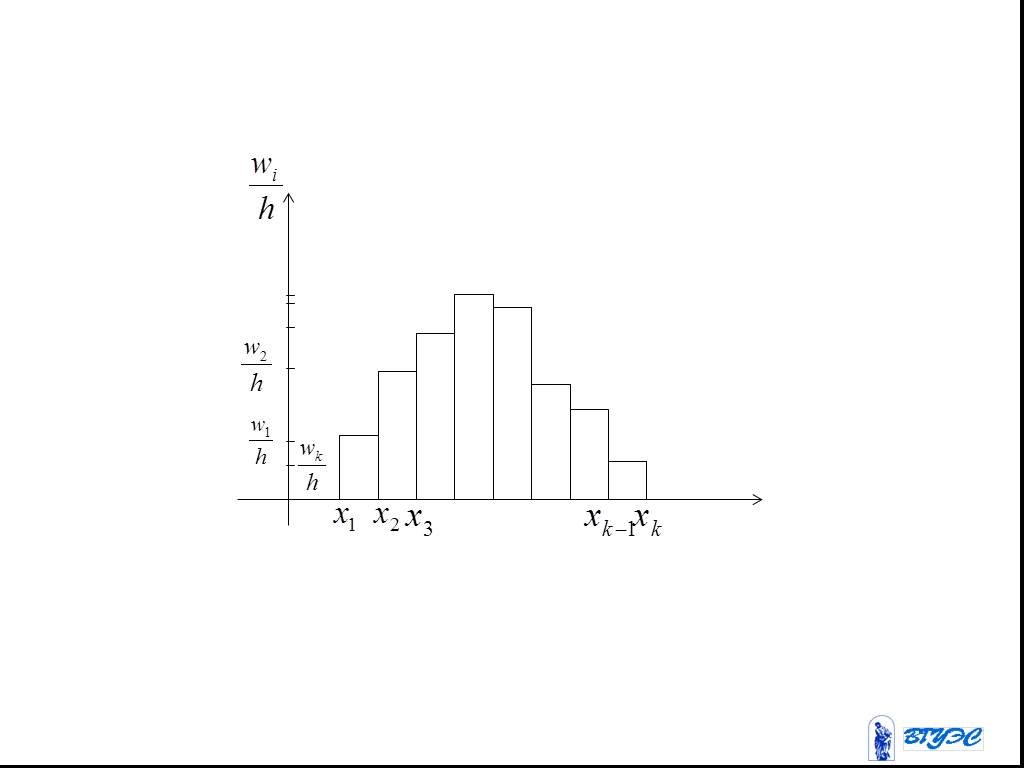
Гистограмма относительных частот

Ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиною , а высоты равны отношению (плотность относительных частот).

Площадь гистограммы относительных частот

тогда

Статистические оценки параметров распределения

Точечные оценки

Оценка, которая определяется одним число, наз. точечной.

Интервальные оценки

Оценка, которая определяется двумя числами, являющимися концами интервала, содержащего неизвестный параметр, называется интервальной.

Свойства точечных оценок

Несмещенность

Статистическая оценка наз. несмещенной, если её математическое ожидание равно оцениваемому параметру при любом объеме выборки:

Эффективность

Статистическая оценка наз. эффективной, если она имеет наименьшую возможную дисперсию.

Состоятельность

Статистическая оценка наз. состоятельной, которая при стремится по вероятности к оцениваемому параметру :

Теорема. Если дисперсия несмещенной оценки при стремится к нулю, то такая оценка состоятельна. Док-во: Оценка параметра несмещенная, т.е. , поэтому при из неравенства Чебышева следует

Но при Значит при , для каждого фиксированного : а Но тогда при

Генеральная средняя

или

Выборочная средняя

Генеральная дисперсия

Выборочная дисперсия

Выборочная средняя является несмещенной и состоятельной:

1.Рассмотрим выборочную среднюю, как случайную величину

т.е.

2.Используем неравенство Чебышева:

Пусть тогда т.е. Значит выборочная средняя является статистической оценкой генеральной средней.

Выборочная дисперсия является смещенной оценкой:

Несмещенная оценка генеральной дисперсии - исправленная выборочная дисперсия:

Статистические характеристики

Мода

Медиана

Асимметрия

Асимметрия распределения характеризуется тем, что вариант, меньших и больших моды неодинаковое число.

При асимметрия положительная; При асимметрия отрицательная.

Если , то распределение почти симметрично; если , то распределение сильно асимметрично.

Эксцесс

Эксцесс характеризует крутовершинность кривой распределения.

Если , то распределение считается близким к нормальному; если , то распределение значительно отклоняется от нормального.

Метод произведений

-условные варианты, -условный нуль.

Статистическая проверка статистических гипотез

Нулевая гипотеза - выдвинутая гипотеза. Конкурирующая гипотеза - - гипотеза, которая противоречит нулевой гипотезе.

Простая гипотеза – гипотеза, содержащая одно предположение:

Сложная гипотеза – гипотеза, которая состоит из конечного или бесконечного числа простых гипотез:

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Уровень значимости – вероятность совершить ошибку первого рода.

Статистический критерий - случайная величина, которая служит для проверки нулевой гипотезы. Наблюдаемым значением - значение критерия, вычисленное по выборке.

Критическая область – совокупность значений критерия, при которых нулевую гипотезу отвергают. Область принятия гипотезы - совокупность значений критерия, при которых нулевую гипотезу принимают. Критические точки - точки, отделяющие критическую область от области принятия гипотезы.

Правосторонняя критическая область – критическая область определяющаяся неравенством: ищут, исходя из требования чтобы

Левосторонняя критическая область – критическая область, определяющаяся неравенством: ищут, исходя из требования чтобы

Двусторонняя критическая область – критическая область, определяющаяся неравенством: ищут, исходя из требования чтобы

Если распределение критерия симметрично относительно 0 и имеются основания выбрать симметричные относительно нуля точки: то Тогда заменится или

Доверительная вероятность (надежность)- вероятность с которой осуществляется неравенство , т.е. Доверительный интервал – интервал, который покрывает неизвестный параметр с заданной надежностью .

Доверительный интервал для оценки математического ожидания нормального распределения при известном .

Число определяется из равенства

Доверительный интервал для оценки математического ожидания нормального распределения при неизвестном

Число определяется по таблице

Критерий согласия – критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Критерии согласия: ( хи квадрат) Пирсона, Колмогорова, Смирнова и др.

Проверка гипотезы о нормальном распределении генеральной совокупности

Критерий Пирсона

В качестве критерия проверки примем случайную величину где -эмпирические частоты; -теоретические частоты.

Строим правостороннюю критическую область, исходя из требования, что в предположении справедливости , где - уровень значимости; - число степеней свободы.

Число степеней свободы находят по формуле где - число групп(частичных интервалов) выборки; - число параметров предполагаемого распределения, которые оценены по данным выборки. Если предполагаемое распределение нормальное, то оценивают два параметра и тогда

Если обозначить , то при гипотезу принимают; при гипотезу отвергают.

Критерий согласия Колмогорова

Если функция распределения случайной величины непрерывна, то практически ее эмпирическая функция распределения при сходится к .

Если непрерывна, то функция распределения величины при имеет пределом функцию которая не зависит от вида функции

По таблице найдем значение функции и затем значение функции Если , то расхождение между эмпирическими и теоретическими функциями распределения несущественно, если , то расхождение существенно.

Сравнение двух дисперсий нормальных генеральных совокупностей

В качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий примем случайную величину , причем отношение большей исправленной дисперсии к меньшей:

Величина при условии справедливости имеет распределение Фишера-Снедекора со степенями свободы и где - объем выборки, по которой вычислена большая исправленная дисперсия.

Элементы теории корреляции

Основные задачи теории корреляции

О форме корреляционной связи между и в виде некоторой функциональной зависимости, которая хотя бы приближенно изображала расплывчатую корреляционную зависимость. Об оценке тесноты корреляционной связи между и , т.е. о степени близости корреляционной зависимости к функциональной.

Регрессии

Регрессией от называется функциональная зависимость между значениями и соответствующими условными средними значениями . Регрессии можно представить геометрически в виде ломанных линий, соединяющих или точки ( ; ), или точки ( ; ).

Эти линии называются эмпирическими (полученными из опыта) ломаными линиями регрессии. Плавную кривую можно получить и иначе, – если ломаную линию регрессии “сгладить” посредством какой-либо известной линии (прямой, параболы, гиперболы и т.п.). Уравнение сглаживающей линии даст хотя и приближенно, но аналитическое – в виде формулы – выражение регрессии. Подобные формулы называют эмпирическими

Задача отыскания эмпирической формулы распадается на две

1. Выбор типа линии, выравнивающей ломанную регрессии, т.е. типа линии, около которой группируются экспериментальные точки ( ; ) или ( ; ). 2. Определение параметров, входящих в уравнение линии выбранного типа, таким образом, чтобы из множества линий этого типа взять ту, которая наиболее близко проходит около точек ломаной регрессии.

Выбор типа линии, выравнивающей ломаную линию регрессии

Для выбора типа линии, выравнивающей ломаную линию регрессии, необходимо хорошо знать простейшие виды линий и их уравнения.

Определения параметров в уравнении выравнивающей линии выбранного типа

Метод средних применяют в тех случаях, когда выбранный тип уравнения выравнивающей линии содержит лишь один параметр. Метод проб используют, когда выбранная формула содержит несколько параметров .

Метод выровненных (или выбранных) точек состоит в выборе по чертежу нескольких точек (не обязательно совпадающих с точками линии регрессии), через которые проводят выравнивающую линию и определяют ее уравнение по координатам этих выбранных точек. Метод наименьших квадратов служит для оценки неизвестных величин по результатам измерений, содержащим случайные погрешности.

Метод наименьших квадратов

Необходимо минимизировать сумму где , – значения опытных данных; – значение функции, взятое из эмпирической зависимости в точке ; – число опытов.

В случае линейной эмпирической формулы сумма принимает вид , а в случае квадратической зависимости – следующий вид: .

Оценка тесноты корреляционной зависимости

Для оценки тесноты корреляционной зависимости служит корреляционное отношение: где – выборочная дисперсия случайной величины , вычисленная по всей таблице; – дисперсия условных средних относительно общей средней, так называемая внешняя дисперсия.

Критерий Фишера

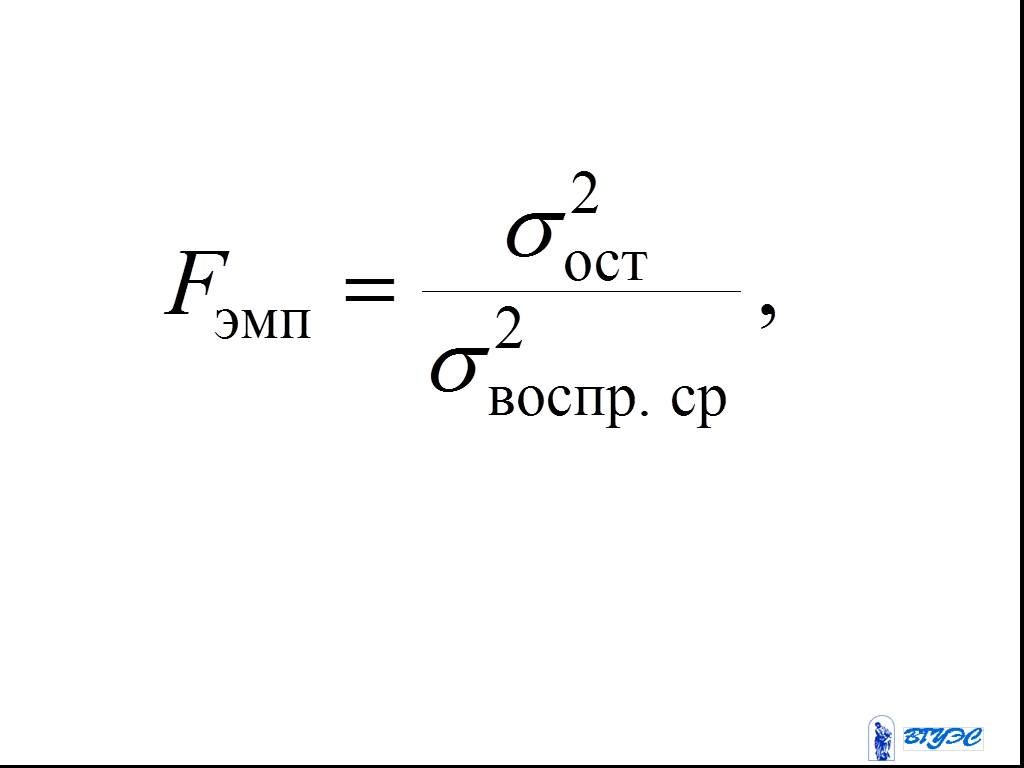
где – остаточная дисперсия; – число коэффициентов в уравнении регрессии; – ордината линии регрессии в точке ; – дисперсия воспроизводимости средних, равная исправленной внутренней дисперсии, деленной на число экспериментов , по которым вычислялись условные средние :

Величина имеет распределение Фишера с числами степеней свободы ( – число задаваемых экспериментатором значений величины , – число проводимых опытов, – число коэффициентов в уравнении регрессии). Из таблицы критических точек распределения Фишера находим .

Если расхождение между теоретической и эмпирической линиями регрессии значимо, уравнение не адекватно, следует взять многочлен более высокого порядка.

Линейная корреляция

Из всех корреляционных зависимостей надо особо выделить линейную корреляцию, т.е. такую, когда точки регрессии располагаются вблизи некоторой прямой линии.

Виды регрессии

1) регрессия на в виде функциональной зависимости ; 2) регрессия на в виде функциональной зависимости .

Выборочный коэффициент корреляции

Выборочное уравнение прямой линии регрессии на

Если данные наблюдений над признаками и заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам : ,