Конспект интегрированного урока алгебры и информатики

по теме «Формула Шеннона. Свойства логарифмов» в 10 классе

Подготовили: Грызайкина Лидия Васильевна, учитель математики МОУ «Средняя общеобразовательная школа №35» г.о. Саранск Республики Мордовия

Аникина Наталья Васильевна, учитель информатики МОУ «Средняя общеобразовательная школа №35» г.о. Саранск Республики Мордовия

Интеграция – средство получения новых представлений на основе традиционных предметных знаний, направлена на развитие эрудиции ученика, на обновление существующей узкой специализации в обучении. Но она не заменяет обучение традиционным предметам, а позволяет соединить получаемые знания в единую систему.

Интеграция является источником нахождения новых фактов, которые подтверждают или углубляют определенные наблюдения, выводы учащихся в различных предметах. Снимает утомляемость, перенапряжение обучающихся за счет переключения на разнообразные виды деятельности, предполагает усиление межпредметных связей, снижение перегрузок учащихся, расширение сферы получаемой информации, подкрепление мотивации обучения.

Интегрированные уроки являются одним из интересных направлений современного образования. На этих уроках формируются следующие компетенции:

• ценностно-смысловые (понимание цели урока, важности изучаемой темы);

• информационные (работа с компьютером, умение самостоятельно подбирать необходимый материал);

• коммуникативные (умение работать в группах, выслушивать, общаться, лояльно относиться к людям с другой точкой зрения).

Тема. Формула Шеннона. Свойства логарифмов. (Презентация)

Цель урока: познакомить учащихся с формулой Шеннона;

повторить свойства логарифмов, формулу перехода от одного основания логарифма к другому;

показать применение формулы Шеннона, свойств логарифмов, формулы перехода от одного основания логарифма к другом при решении задач.

Ход урока.

1. Орг. момент

2.Учитель информатики. Повторение.

1. Чему равен информационный объем одного символа английского алфавита?

2. Была получена телеграмма: «Встречайте вагон 11». Известно, что в составе поезда 32 вагона. Какое количество информации было получено?

3. При угадывании целого числа в диапазоне от 1 до N было получено 6 бит информации. Чему равно N?

4. Запишите формулу Хартли?

3.Учитель математики. Повторение.

1. Как называется уравнения вида а^х = b (а > 0,a ≠ 1, b > 0?

(Ответ. Показательное)

2. Сколько корней имеет показательное уравнение?

(Ответ. Один)

3. Чему равен корень уравнения 2^х = N?

(Ответ. х = log₂ N)

4. Вычислите:

а) log₂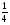; б) log₃9; в) log₂16; г) log₂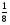; д) log₄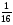; е) log₂ .

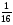(Ответ. а) – 2; б) 2; в) 4; г) – 3; д) – 2; е) – 4)

5. Какие из перечисленных логарифмов являются отрицательными?

а) log₄ 8; б) log₂16; в) log₂(1/16); г) log₂0,8; д) log₄0,04.

(Ответ. в, г, д)

6. Сравните с нулем log_а в, если

а) а >1, в >1; б) 0 1, в >1; в) а >1, 0 1.

(Ответ. а) log_а в>0, б) log_а вlog_а в

4. Учитель информатики. Изучение нового материала.

Сегодня мы рассмотрим вероятностный подход к определению количества информации, запишем формулу Шеннона, а также будем учиться решать задачи, используя эту формулу.

Формула Хартли используется для определения количества информации, которое несет равновероятное событие и не справедлива в системе неравновероятных событий.

В системах с неравновероятными событиями удобно использовать формулу Шеннона. Эту же формулу можно использовать и в системе равновероятных событий, в этом случае формула Хартли будет частным случаем формулы Шеннона.

Клод Шеннон предложил свою теорию для определения количества информации в 1948 году. Однако еще в XIX веке аналогичное выражение было получено Больцманом. Он получил его как формулу для энтропии, когда занимался проблемами статической физики. Энтропия физической системы служит мерой неопределенности системы. Энтропия – среднее количество информации, приходящееся на одно состояние физической системы.

С точки зрения теории информации можно считать, что энтропия системы является мерой неопределенности состояния элементов системы. Однако и количество информации рассматривают как меру уменьшения неопределенности состояния системы. Эта интерпретация позволяет легко понять, почему Больцман получил такую же формулу, как и Шеннон для определения количества информации.

Формула Шеннона имеет вид: ,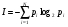

где I – количество информации; N – количество возможных событий; p_i – вероятности отдельных событий.

Можно заметить, что если вероятности p₁, p₂, …, p_n равны между собой, то каждую из них можно найти следующим образом: 1/N.

Пусть имеется источник информации, который выдает последовательность символов некоторого алфавита, при этом разные символы могут встречаться с разной частотой.

Пусть имеется алфавит, состоящий из N символов с частотной характеристикой p₁, p₂, …, p_i, где p_i выражает вероятность появления i-го символа. Вероятность неотрицательна (p_i ≥ 0) и их сумма равна 1. Тогда средний информационный вес символа такого алфавита выражается формулой: .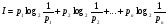

Используя вышесказанное, решим задачу №1:

Задача №1. За контрольную работу по информатике получено 8 «пятерок», 4 «четверки», 2 «тройки» и 2 «двойки». Какое количество информации получил ученик Васечкин, увидев свою оценку в тетради?

Решение:

N=8+4+2+2=16 – количество оценок

p=K/N,

р₅=8/16=1/2,

р₄=4/16=1/4,

р₃=р₂=2/16=1/8.

I = – (0,5 log₂ (0,5) + 0,25 log₂ (0,25) +0,125 log₂ (0,125) +0,125 log₂ (0,125)).

5. Учитель математики. Решение задачи № 1.

Используя определение логарифма, найдем значение данного выражения:

I = – (0,5 log₂ (0,5) + 0,25 log₂ (0,25) +0,125 log₂ (0,125) +0,125 log₂ (0,125))=

= – (0,5·(–1) +0,25·(–2) +0,125·(–3) +0,125·(–3)) = – (– (0,5+0,5+0,375+0,375))=

= 1+0,75 = 1,75.

(Ответ. 1,75)

6. Учитель информатики. Решение задачи № 2.

Задача № 2. В непрозрачном мешочке хранятся 8000 белых, 2000 красных, 40000 синих бусинок. Какое количество информации будет содержать зрительное сообщение о цвете вынутой бусинки?

Решение:

Так как количество бусинок различных цветов неодинаково, то вероятности зрительных сообщений о цвете вынутой из мешочка бусинки также различаются и равны количеству бусинок данного цвета, деленному на общее количество.

N=8000+2000+40000=50000

p=K/N,

р_Б=8000/50000=0,16;

р_К=2000/50000=0,04;

р_С=40000/50000=0,8.

События неравновероятны, поэтому снова воспользуемся формулой Шеннона

7. Учитель математики. Повторение. Для решения этой задачи нам необходимо знать свойства логарифмов. Давайте вспомним их.

7) Чему равен логарифм произведения?

(Ответ. Логарифм произведения двух множителей равен сумме логарифмов этих множителей.)

8) Чему равен логарифм частного?

(Ответ. Логарифм частного двух чисел равен разности логарифмов делимого и делителя.)

Мы с вами уже встречались с логарифмами, значения которых нельзя вычислить, не прибегая к микрокалькулятору или специальным таблицам. Это таблицы десятичных и натуральных логарифмов. Но также мы понимаем, что невозможно составить таблицы для всех случаев, так как основанием логарифма может быть любое положительное число. Как поступают в таких ситуациях?

9) Записать формулу перехода от одного основания логарифма к другому.

(Ответ. log_а в = log_с в /log_с а)

10) Какой логарифм называется десятичным? Как он обозначается?

(Ответ. Логарифм по основанию 10 называется десятичным и обозначается lgв)

11) Записать формулу перехода от логарифма по основанию 2 к логарифму по основанию 10.

(Ответ. log₂в = lgв/lg2)

12) Представьте log_1/2 в и log₂ (1/в) так, чтобы числа а и в были больше 1.

Что можно сказать об этих числах?

(Ответ. – log₂ в. Они равны)

8. Учитель математики. Решение задачи № 2.

I = – (0,16·log₂ (0,16) + 0,04·log₂ (0,04) +0,8·log₂ (0,8)) = (*)

Прежде чем приступить к вычислению I, отдельно вычислим значения логарифмов, встречающихся в выражении (*): log₂ 0,16, log₂ 0,04, log₂0,8.

Для этого воспользуемся компьютерным калькулятором Wise Calculator:

1. log₂ 0,16 = log₂ 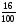= log₂16 – log₂100 = 4 – log₂100 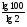= 4 – =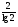

= 4 – = 4 – 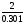= 4 – 6,645 = – 2,645;

2. log₂ 0,04 = log₂ 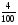= log₂ 4 – log₂100 = 2 – log₂100 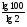= 2 – =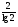

= 2 – = 2 – 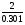= 2 – 6,645 = – 4,645;

3. log₂ 0,8 = log₂ 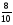= log₂8 – log₂10 = 3 – log₂10 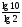= 3 – = 3 – =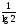

= 3 – 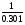= 3 – 3,322 = – 0,322.

Теперь решение нашей задачи будет выглядеть так:

I = – (– (0,16·2,645 + 0,04·4,645 + 0,8·0,322)) = 0,4232 + 0,1858 + 0,2576 = 0,866

(Ответ. 0,87)

Итог урока.

Домашнее задание. Алгебра и начала анализа: §16, 17, № 303, 304.

Информатика: §2.4, № 2.5, 2.6;

Список литературы.

1. Алгебра и начала анализа. Учебник для 10 – 11 классов/ А.Ш. Алимов, Ю.М. Колягин – М.: Просвещение, 2012

2. Дидактические материалы по алгебре и началам анализа для 10 класса/

Б.М. Ивлев, С.М. Саакян, С.И. Шварцбург. – М.: Просвещение, 2011.

3. Информатика. Учебник для 10 – 11 классов/ И.Г. Семакин – М.: Бином, 2011.

4. Информатика и информационные технологии. Учебник для 10 – 11 классов/ Н.Д. Угринович. – М.: Бином. Лаборатория знаний, 2011.