Конспект урока «УРОК-КВН» по математике для 11 класса
Муниципальное бюджетное общеобразовательное учреждение
Донская средняя общеобразовательная школа
УРОК-КВН
Подготовила:
Учитель математики
Первой категории
Естремская Лидия Ивановна
Возраст детей: 11 класс
х.Гундоровский
2013
Урок-КВН
Тема: Применение производной
Тип урока: зачёт-практикум
Цели урока: обобщение изученного материала по теме, формирование умений применять математические знания к решению практических задач, воспитание
познавательного интереса к предмету.
Оборудование: интерактивная доска, тексты тестов для каждого ученика, карточки с заданиями, цветные мелки, указка.
Правила игры:
-
Класс разбивается на 2 команды
-
Выбираются капитаны команд
-
Капитаны назначают консультантов
-
Для участия во всех видах работы вызываются к доске капитанами команд
Ход урока
1 этап. Разминка (прил.1)
Каждый ученик получает текст теста, работает с ним. Побеждает та команда, у которой больше сумма баллов. Проверку осуществляет команда-соперница. Правильные ответы проецируются на доску.
2 этап. Блицтурнир (на доску проецируются задания)
| Правильные ответы: | |||
| а) |
|
|
|
| б) |
|
|
|
| в) |
|
|
|
| г) |
|
|
|
| д) |
|
|
|
(За найденную ошибку команда получает 1 балл)
-
этап. Конкурс капитанов
Капитан каждой команды получает карточку с текстом задачи, решает её.
Представьте число 12 в виде суммы двух положительных слагаемых так, чтобы сумма их квадратов была наименьшей.
Имеется проволока длиной а метров. Требуется оградить этой проволокой прямоугольный участок земли, одна сторона которого примыкает к стене заводского здания, так, чтобы площадь огороженного участка была наибольшей.
Ответы: 1) 6 и 6 2) ![]()
Тем временем учащиеся решают задачи капитанов из противоположных команд и готовят для них вопросы по теме задания.
По результатам решения задачи и ответов на вопросы капитаны получают баллы.
-
этап. Конкурс консультантов
Исследуйте и постройте график функции:
-
этап. Конкурс эрудитов
-
В какой точке касательная к графику функции
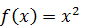 параллельна прямой у=2х+5?
параллельна прямой у=2х+5? -
В какой точке касательная к графику функции
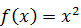 перпендикулярна прямой у=2х+5?
перпендикулярна прямой у=2х+5?
(задания записаны на карточках)
Ответы: 1. М(1;1) 2. N ![]()
6 этап. Конкурс учителей-методистов
(домашнее задание)
Двум-трём ученикам от каждой команды предлагается продемонстрировать, как бы они объяснили в 1 классе одно из понятий (функция, максимум, минимум, и др.)
7 этап. Подведение итогов
Объявляется команда-победительница, а многие учащиеся получают оценку.
8 этап. Домашнее задание
(дифференцированно)
Придумать задачи практического содержания на нахождение наибольшего и наименьшего значений функции.
Учащимся, которые интересуются математикой и готовящимся к поступлению в вузы, предлагаются задания, которые публикуются в журналах «Математика в школе», сборниках для поступающих в вузы.
Приложение 1
Тест
-
Найди производную функции
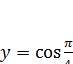 .
.
-
-1 2) -
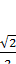 3) 0 4)
3) 0 4) 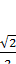 5) 1
5) 1
-
Найди наименьшее значение функции
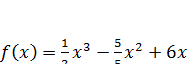 на отрезке
на отрезке 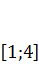
-
 2)
2) 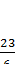 3)
3)  4)
4)  5)
5) 
-
Найди область определения функции, заданной формулой
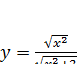
-
все числа 2)
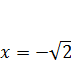 3)
3) 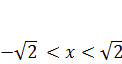 4)
4) 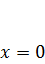
5) верного ответа нет
-
Укажите верное утверждение:
а) любая функция имеет наибольшее значение;
б) любая, ограниченная сверху функция имеет наибольшее значение;
в) если некоторое число ограничивает сверху все значения функции и совпадает с тем из них, то это число - наибольшее значение функции;
г) если некоторое число А ограничивает сверху все значения функции и никакое меньшее число их не ограничивает, то число А является наибольшим значением функции;
д) если некоторое число - наибольшее значение функции, то во всех точках, кроме одной, функция принимает значения, меньшие этого числа.
-
а 2) б 3) в 4) г 5) д
-
Укажите, какие из утверждений являются верными:
а) если функция определена в целой окрестности некоторой точки, то она дифференцируема в этой точке;
б) если функция недифференцируема в некоторой точке, то она не является непрерывной в этой точке;
в) если функция дифференцируема в некоторой точке, то она непрерывна в этой точке;
г) если функция непрерывна в некоторой точке, то она дифференцируема в этой точке.
1) а и в 2) в 3)в и г 4)б и г 5)а и б
Литература
-
Журналы «Математика в школе»
-
М.П.Галицкий и др. «Углубленное изучение курса алгебры и начала математического анализа»
-
Черкасов О.Ю «Математика. Скорая помощь абитуриентам»
-
В.С.Крамор «Повторяем и систематизируем школьный курс алгебры и начал анализа»
-
В.А.Васильева и др. «Методическое пособие по математике для поступающих в вузы»
Здесь представлен конспект к уроку на тему «УРОК-КВН», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.
