Конспект урока «Решение познавательных задач с положительными и отрицательными числами» по математике для 6 класса
Тип урока:
урок решения познавательных
задач с элементами игры.
Решение познавательных задач
с положительными и отрицательными числами (6 класс)
Цели урока: 1) образовательная: отработка и закрепление умений и навыков решения познавательных задач с положительными и отрицательными числами; выработка у учащихся умения обобщать изученный материал, анализировать, сопоставлять и делать выводы; 2) воспитательная: формирование навыков самоконтроля; воспитание терпеливости при выполнении задания, чувства ответственности за проделанную работу; 3 ) развивающая: развитие памяти, логического мышления, сообразительности, внимания.
Оборудование: написанные на доске примеры для устной работы, задания на карточках для самостоятельной работы, бумажное «домино» (см. задание), разноцветные треугольники с цифрами (см. задание), «лента времени» (см. задание), учебники.
Предварительная подготовка к уроку: учащиеся должны знать следующие темы: «Противоположные числа», «Модуль числа», «Сравнение чисел», «Сложение отрицательных чисел», «Сложение чисел с разными знаками», «Вычитание», «Умножение», «Деление», владеть навыками работы с положительными и отрицательными числами.
Ход урока
I. Устная работа.
-
Игра «Домино». (Приготовить из бумаги костяшки домино и закрепить их на доске. Цель: развитие у обучающихся внимательности и умения быстро принимать правильное решение). Сложите костяшки домино так, чтобы соединялись противоположные числа.
5 и - 4, 8 и 4, - 4 и 2, - 2 и 7, - 7 и - 10, 10 и - 11, 11 и 5.
-
(На доске прикреплены изображения яблок, кубиков и т.д. с надписями чисел. Корзинки изготовлены из бумаги. На одной из них написаны противоположные числа, на другой - взаимно обратные числа. Необходимо собрать фигурки в соответствующие корзинки. Цель: развитие внимательности и быстроты реакции. Задание выполняют у доски два человека на скорость). Соберите в корзинки яблоки (кубики и т.д.) так, чтобы пары попали в правильные корзинки.
- 5, - 4, 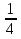 , - 5, 4, -
, - 5, 4, - 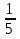 , -
, -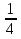 ,
, 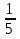 и т.д.
и т.д.
3. (На доске прикреплены разноцветные треугольники с написанными на них числами. Необходимо из них построить домики, учитывая, что из трех фигур можно построить только одно здание. Цель: воспитание интереса к предмету во время выполнения познавательного задания, развитие пространственного воображения. Можно добавить и свои пары чисел. Ниже приводится вариант такого задания.) Из 3 треугольников можно построить домик. Но для него подойдут только те из них, числа которых имеют больший модуль.
1) Для первого домика: 10 и – 7, - 5 и 2, - 8 и – 9.
2) Для второго домика: 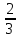 и -
и - 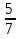 , 1
, 1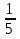 и - 3
и - 3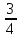 , 7
, 7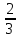 и - 7
и - 7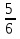 .
.
Ответы: 1) – 10, - 5, - 9; 2) - -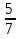 , - 3
, - 3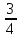 , - 7
, - 7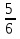 .
.
4.Найдите числа, которые спрятались за звездочками, учитывая, что за * и ** скрыты разные числа, но за одной (* или **) – числа одинаковые.
- 7 ∙ ** = *
- 28 : * =*
- 5 ∙ ** + 8 – 2 ∙ ** = 22
Ответы: ** = - 2, * = 14.
II. Выполнение заданий
-
Выполните действия с модулями:
-
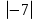 - 2 .
- 2 .
Решение: 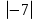 - 2 = 7 – 2 = 5.
- 2 = 7 – 2 = 5.
Ответ: 5.
-
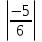 +
+ 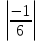 .
.
Решение: 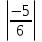 +
+ 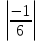 =
= 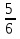 +
+ 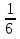 =
= 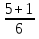 =
= 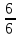 = 1.
= 1.
Ответ: 1.
-
– 2,5 +
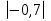 .
.
Решение: – 2,5 + 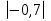 = -2,5 + 0,7 = - 1,8.
= -2,5 + 0,7 = - 1,8.
Ответ: - 1,8.
-
– 43,6 + 37,6 +
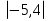 .
.
Решение: – 43,6 + 37,6 + 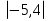 = - 6 + 5,4 = - 0,6.
= - 6 + 5,4 = - 0,6.
Ответ: - 0,6.
-
Представьте число – 15 в виде разности:
-
Двух положительных чисел.
Решение: так как в ответе должно получиться отрицательное число, то при разности двух положительных чисел уменьшаемое должно быть меньше вычитаемого. Например, 15 – 30 = - 15, 24 – 39 = - 15, 18 – 33 = - 15 и т.д.
-
Двух отрицательных чисел.
Решение: так как в ответе должно получиться отрицательное число, то при разности двух отрицательных числе модуль уменьшаемого должен быть больше модуля вычитаемого. Например, - 30 – (- 15) = - 15, - 39 – (- 24) = - 15, - 33 – (- 18) = - 15 и т.д.
-
Отрицательного и положительного чисел.
Решение: так как в ответе должно получиться отрицательное число, то при разности отрицательного и положительного числа уменьшаемое может быть как меньше вычитаемого, так и больше. Потому что в итоге получается, что мы складываем два отрицательных числа. Например, - 7 – 8 = - 15, - 5 – 10 = - 15, - 12 – 3 = - 15 и т.д.
-
Найдите значение выражения -
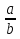 + 3c:
+ 3c:
-
Если a = 10, b = - 2, c = 4.
Решение: если a = 10, b = - 2, c = 4, то - 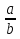 + 3c = -
+ 3c = - 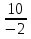 + 3 ∙ 4 = 5 + 12 = 17.
+ 3 ∙ 4 = 5 + 12 = 17.
Ответ: 17.
-
Если a = - 18, b = - 3, c = - 5.
Решение: если a = - 18, b = - 3, c = - 5, то - 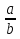 + 3c = -
+ 3c = - 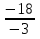 + 3 ∙ ( - 5) = - 6 – 15 = - 21.
+ 3 ∙ ( - 5) = - 6 – 15 = - 21.
Ответ: - 21.
-
Заполните пропущенные элементы цепочки. (Ученики могут также проверить, правильно ли выполнили задание.)
| * : (- | * + | * - | * : | * + (- | - 4 |
Решение:
-
-
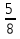 ∙
∙ 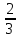 = -
= - 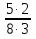 = -
= - 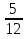 .
. -
-
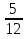 : (-
: (- 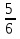 ) =
) = 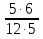 =
= 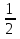 .
.
-
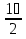 +
+ 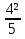 =
= 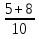 =
= 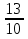 =
= 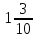 .
.
-
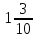 -
- 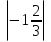 =
= 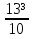 -
- 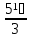 =
= 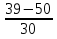 = -
= - 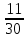 .
.
-
-
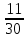 :
: 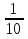 = -
= - 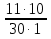 = -
= - 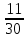 = -
= - 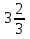 .
.
-
-
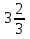 + (-
+ (- 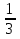 ) = -
) = - 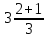 = -
= - 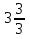 = - 4.
= - 4.
Элементы цепочки восстановлены верно.
Ответ:
| - |
|
| - | - | - 4 |
III. Устная работа
-
Ответьте, не решая примера, какое получится при выполнении действия число: положительное или отрицательное.
-
- 1∙ 2 ∙ 4 ∙ (- 7) ∙ (- 3) ∙ 8.
Ответ: при умножении встречаются три отрицательных числа. При умножении двух отрицательных чисел мы получаем положительное число. Но если мы умножим его на отрицательное число, то получим отрицательное число. Следовательно, при решении данного примера ответ будет отрицательным.
-
100 : (- 2) : 5 ∙ 2 : 3 : (-1).
Ответ: при делении встречаются два отрицательных числа. При делении двух отрицательных чисел мы получаем положительное число. Следовательно, при решении данного примера ответ будет положительным.
-
Составьте «ленту времени». Для этого расположите числа по порядку, соответственно, буквы тоже встанут на свои места. В результате вы получите математический термин, который использовали при выполнении данного задания. Данный термин состоит из двух слов. Чтобы узнать, какое слово первое, необходимо расположить числа в порядке возрастания. Для второго, наоборот, числа нужно расположить в порядке убывания.
| - 6 | 0 | - 2 | 4 | 1 | 5 | - 3 | 3 | - 1 | - 5 | - 4 | |
| т | к | н | д | а | а | я | р | н | и | о | о |
Первое слово
Ответ:
| - 5 | - 4 | - 3 | - 2 | - 1 | 0 | 1 | 2 | 3 | 4 | 5 | |
| к | о | о | р | д | и | н | а | т | н | а | я |
Второе слово
| - 2 | 2 | 1 | - 1 | 3 | |
| м | я | р | я | а | п |
Ответ:
| 2 | 1 | 0 | - 1 | - 2 | |
| п | р | я | м | а | я |
IV. Выполнение заданий
-
Сравните выражения:
-
-
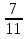 - (-
- (-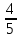 ) и – 0,2 - (-
) и – 0,2 - (-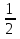 ).
).
Решение: найдем значение выражений.
- 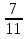 - (-
- (-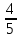 ) = -
) = - 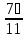 +
+ 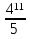 =
= 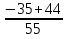 =
= 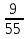 .
.
- 0,2 - (-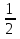 ) = -
) = - 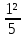 +
+ 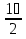 =
= 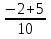 =
= 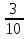 .
.
Приведем значение выражений к общему знаменателю:
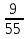 =
= 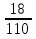 и
и 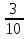 =
= 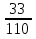 . Значит,
. Значит, 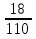 . Следовательно, -
. Следовательно, - 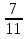 - (-
- (-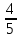 ) – 0,2 - (-
) – 0,2 - (-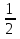 ).
).
Ответ: - 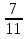 - (-
- (-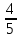 ) – 0,2 - (-
) – 0,2 - (-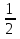 ).
).
-
– 5,5 ∙ 2 + (- 4,3) и – 4,3 – 2,2 ∙ 5.
Решение: найдем значения выражений.
– 5,5 ∙ 2 + (- 4,3) = - 11 – 4,3 = - 15,3.
– 4,3 – 2,2 ∙ 5 = - 4,3 – 11 = - 15,3.
Так как – 15,3 = - 15,3, выражения равны: – 5,5 ∙ 2 + (- 4,3) = – 4,3 – 2,2 ∙ 5.
Ответ: – 5,5 ∙ 2 + (- 4,3) = – 4,3 – 2,2 ∙ 5.
-
Исключите лишний пример в строчке:
-
– 5,5 + 4,3; 2,2 – 1,3; - 3,7 + 4,5.
Решение: при вычислении получается одно отрицательное число (- 1,2) (пример 1).
Ответ: - 5,5 + 4,3.
-
– 6,5 + 6,1, -
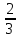 + (-
+ (-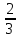 ), -
), - 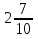 -
-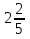 .
.
Решение: при вычисление получается одно число, у которого есть целая часть - 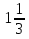 (пример 2).
(пример 2).
Ответ: - 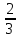 + (-
+ (-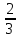 ).
).
-
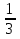 ∙
∙ 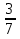 ,-
,- 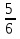 :
: 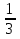 ,
, 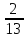 : (-
: (- 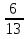 ).
).
Решение: при вычислении получается одна дробь, которую можно перевести в десятичную без остатка (- 2,5) ( пример 2).
Ответ: - 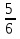 :
: 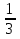 .
.
-
Найдите значение выражения:
-
( - 0,5 + ( -
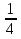 )) ∙ 2 a, если a = - 3,7.
)) ∙ 2 a, если a = - 3,7.
Решение:
Первый способ.
Преобразуем данное выражение: - 0,5 + (-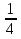 ) = - 0,5 – 0,25 = - 0,75.
) = - 0,5 – 0,25 = - 0,75.
Отсюда получим: - 0,75 ∙ 2a.
Если a = - 3,7, то – 0,75 ∙ 2a = - 0,75 ∙ 2 ∙ ( - 3,7) = - 1,5 ∙ (3 3,7) = 5,55.
Второй способ.
Преобразуем данное выражение: - 0,5 + (-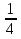 ) = - 0,5 – 0,25 = - 0,75.
) = - 0,5 – 0,25 = - 0,75.
Отсюда получим: - 0,75 ∙ 2a. Его снова можно преобразовать: - 0,75 ∙ 2a = - 1,5a.
Если a = - 3,7, то - 1,5a = - 1,5∙ (- 3,7) = 5,55.
Ответ: 5,55.
-
( - 0,1 + (-
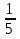 )) ∙
)) ∙ 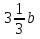 , если b = - 2,75.
, если b = - 2,75.
Решение:
Первый способ.
Преобразуем данное выражение: - 0,1 + (-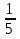 ) = - (
) = - (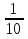 +
+ 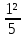 ) = -
) = - 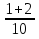 = -
= - 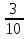 . Отсюда получим: -
. Отсюда получим: - 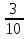 ∙
∙ 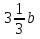 .
.
Если b = - 2,75, то - 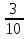 ∙
∙ 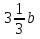 = -
= - 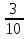 ∙
∙ 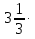 ( - 2,75) = -
( - 2,75) = -  ∙ (- 2,75) = - 1 ∙ (- 2,75) = 2,75.
∙ (- 2,75) = - 1 ∙ (- 2,75) = 2,75.
Второй способ.
Преобразуем данное выражение: - 0,1 + (-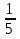 ) = - (
) = - (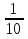 +
+ 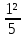 ) = -
) = - 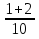 = -
= - 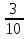 . Отсюда получим: -
. Отсюда получим: - 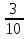 ∙
∙ 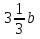 . Его снова можно преобразовать: -
. Его снова можно преобразовать: - 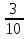 ∙
∙ 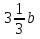 = -
= - 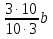 = - 1b =- b.
= - 1b =- b.
Если b = - 2,75, то – b = - (- 2,75) = 2,75.
Ответ: 2,75.
-
Найдите значение суммы и разности:
-
– 2,3 + (- 2,4 + (- 2,5)).
2 1
Решение: – 2,3 + (- 2,4 + (- 2,5)).
-
– 2,4 + (- 2,5) = - (2,4 + 2,5) = - 4,9;
-
– 2,3 + (- 4,9) = - (2,3 + 4,9) = 7,2.
Ответ: 7,2.
-
(-
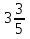 + (-
+ (-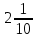 )) -
)) - 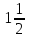 .
.
1 2
Решение: (-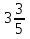 + (-
+ (-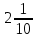 )) -
)) - 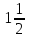 .
.
-
-
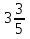 + (-
+ (-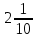 ) = - (
) = - (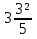 +
+ 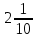 ) = - 5
) = - 5 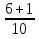 = - 5
= - 5 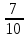 ;
; -
- 5
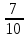 -
- 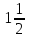 = (5
= (5 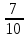 +
+ 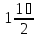 ) = - 6
) = - 6 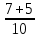 = - 6
= - 6 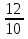 = - 6
= - 6 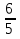 = - 7
= - 7 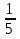 .
.
Ответ: - 7 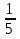 .
.
V. Итог Урока
VI. Самостоятельная работа
Преобразуйте выражения и найдите ответы в квадратиках. Рядом (справа) будут числа, которые нужно выписать. Из них составьте сумму и решите получившийся пример.
-
2
3,7
5,6
- 1,8
- 4,5
5
- 7,4
- 0,8
- 8
- 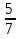 : (- 1
: (- 1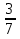 ) + 2,5 : (- 0,8) – 0,3.
) + 2,5 : (- 0,8) – 0,3.
1 3 2 4
Решение: - 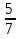 : (- 1
: (- 1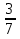 ) + 2,5 : (- 0,8) – 0,3.
) + 2,5 : (- 0,8) – 0,3.
-
-
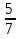 : (- 1
: (- 1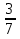 ) =
) = 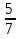 :
: 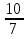 =
= 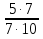 =
= 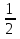 ;
; -
2,5 ∙ (- 0,8) = - 2;
-
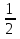 + (- 2) = 0,5 – 2 = - 1,5;
+ (- 2) = 0,5 – 2 = - 1,5; -
– 1,5 – 0,3 = - 1,8.
При решении получилась цифра – 1,8. Справа от нее расположена цифра – 4,5.
-
3
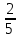
- 4
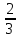
4
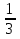
- 2,78
- 4,5
3,57
6,8
4
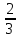
9,5
( 5 - 2 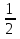 ) :
) : 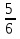 + (4 - 2
+ (4 - 2 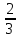 ) :
) : 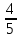 .
.
1 2 5 3 4
Решение: ( 5 - 2 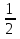 ) :
) : 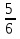 + (4 - 2
+ (4 - 2 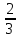 ) :
) : 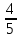 .
.
-
5 - 2
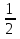 = 4
= 4 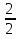 - 2
- 2 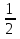 = 2
= 2 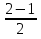 = 2
= 2 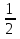 ;
; -
2
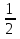 :
: 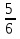 =
= 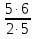 = 3;
= 3; -
4 - 2
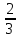 = 3
= 3 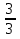 - 2
- 2 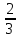 = 1
= 1 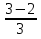 = 1
= 1 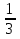 ;
; -
1
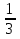 :
: 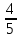 =
= 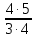 =
= 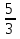 = 1
= 1 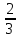 ;
; -
3 + 1
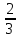 = 4
= 4 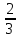 .
.
При решении получилась цифра 4 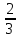 . Справа от нее расположена цифра 9,5.
. Справа от нее расположена цифра 9,5.
Сложим цифры – ответы из обоих квадратиков. Получим – 4,5 + 9,5 = 5.
Ответ: 5.
Здесь представлен конспект к уроку на тему «Решение познавательных задач с положительными и отрицательными числами», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (6 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

