Конспект урока «Методы использования ограниченности функций» по математике для 11 класса

Тема: Методы использования ограниченности функций.
Жизнь хороша тем, что в ней
можно заниматься математикой.
(Леонард Эйлер)
Цели: развитие нового нешаблонного мышления, которое можно успешно применять и в других сферах человеческой деятельности (кибернетика, вычислительная техника, экономика, радиофизика, химия и др).
Задачи: - обучение оценке объективной и субъективной трудности заданий и, разумному выбору этих заданий на экзамене;
- создание «копилки» нетрадиционных и необычных рассуждений.
Ход урока:
-
Орг. момент. Формулирование учащимися темы урока посредством выполнения заданий ЕГЭ части А и В и расшифровке темы по убыванию полученных ответов. ( В качестве предполагаемых слов зашифровать 12 карточек под номерами от -2 до 10) (приложение 1 и 2 )
| метод | использования | функций | |
| Найти абсциссу точки графика функции у=3х2-7х+7, в которой тангенс угла касательной равен -1. | Найти значение выражения | Укажите наибольшее значение функции У=3-2sin5х | Решите уравнение |
| Ответ: 1 | Ответ: 10 | Ответ: 5 | Ответ: -1 |
2. Разделить учащихся на 2 группы, вручить им набор « Теория + 10 заданий» (приложение 3 и 4 ), попросить выбрать те задания, которые можно выполнить по данной теоретической части, обосновать свой выбор.
3. Показать ход выполнения этих заданий на доске учащимися: Носкова К. , Дедевшин И., Веселов И.
4. Разделить задания из карточки на 2 группы для решения их с последующей самопроверкой по листу готовых решений. ( приложение 5)
5. Раздать группам листы с описанием новых нестандартных методов решения уравнений и неравенств для выбора следующей темы ( в качестве дом. задания отыскать в сборниках ЕГЭ задачи, которые можно решать этим методом)( приложение 6 )
6. Рефлексия учащихся ( заполнение таблички)
| Какое функциональное свойство использовали на уроке? | Свою работу Вы оцениваете на оценку……? | Практическая значимость данного метода для Вас составляет (от 0 до 5 баллов) | |
| | | | |
Приложение 1.
Решите эти задания и расположите ответы в порядке убывания, соберите по ответам тему нашего занятия.
| Найти значение выражения | Укажите наибольшее значение функции У=3-2sin5х | Решите уравнение | |
| Ответ: | Ответ: | Ответ: | Ответ: |
| | | |
Приложение 2.
9 2 0 7
Исследование функций с помощью производной.
10 5 1 -1
Метод использования ограниченности функций.
4 -2 8 12
Решение неравенств графическим способом.
3 11 6
Решения функциональных уравнений.
| функций | с помощью | производной | |
| Метод | использования | ограниченности | функций |
| Решение | неравенств | графическим | способом |
| Решение | функциональных | уравнений | |
| 2 | 0 | 7 | |
| 10 | 5 | 1 | -1 |
| 4 | -2 | 8 | 12 |
| 3 | 11 | 6 | |
Приложение 3.
Одним из эффективных методов решения уравнений или неравенств является метод, основанный на использовании ограниченности функций. К наиболее известным ограниченным функциям относятся, например, некоторые тригонометрические; обратные тригонометрические функции; функции, содержащие модуль, степень, корень с чётной степенью и другие.
Наиболее распространёнными неравенствами являются следующие:
│f(x)│≥0, -1≤sinx≤1, -1≤cosx≤1, -![]()
![]() -
-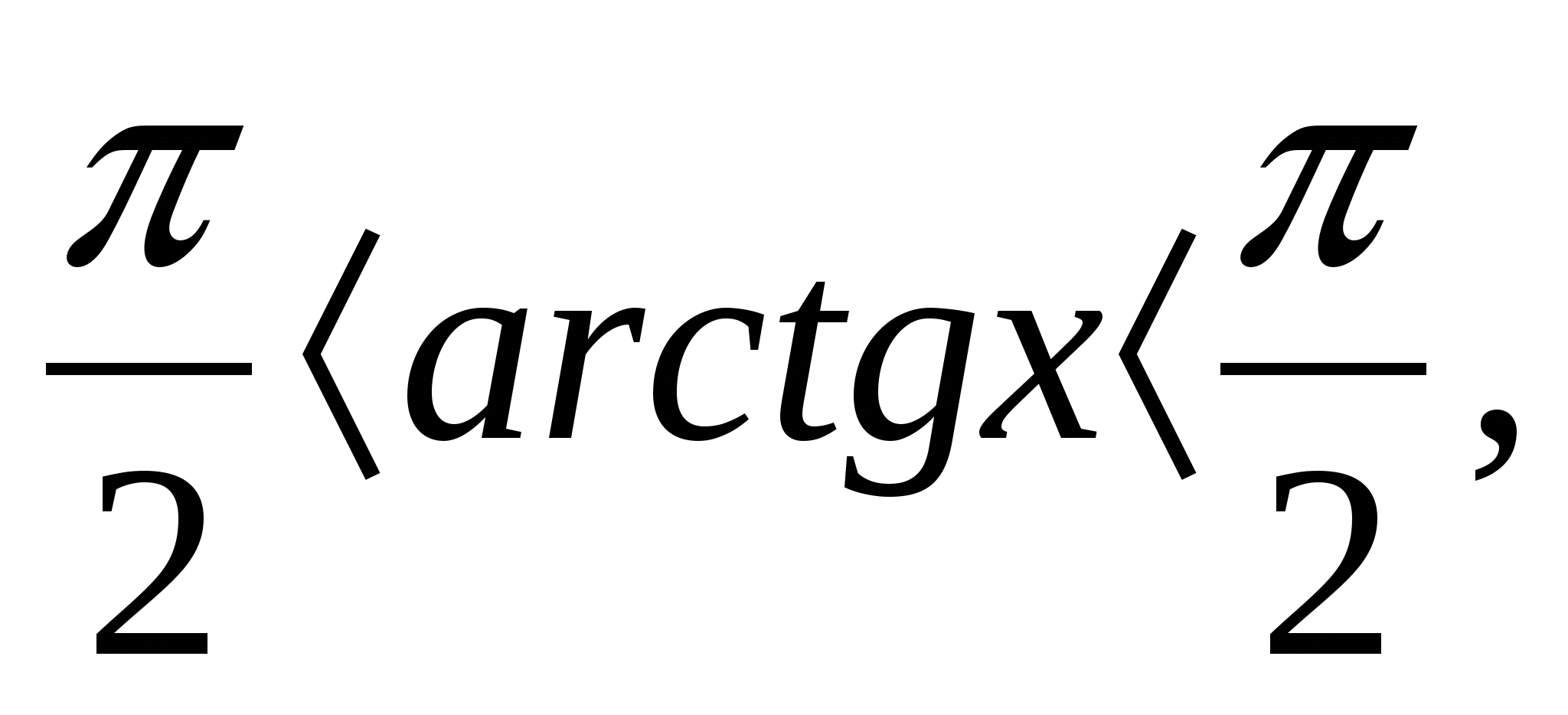
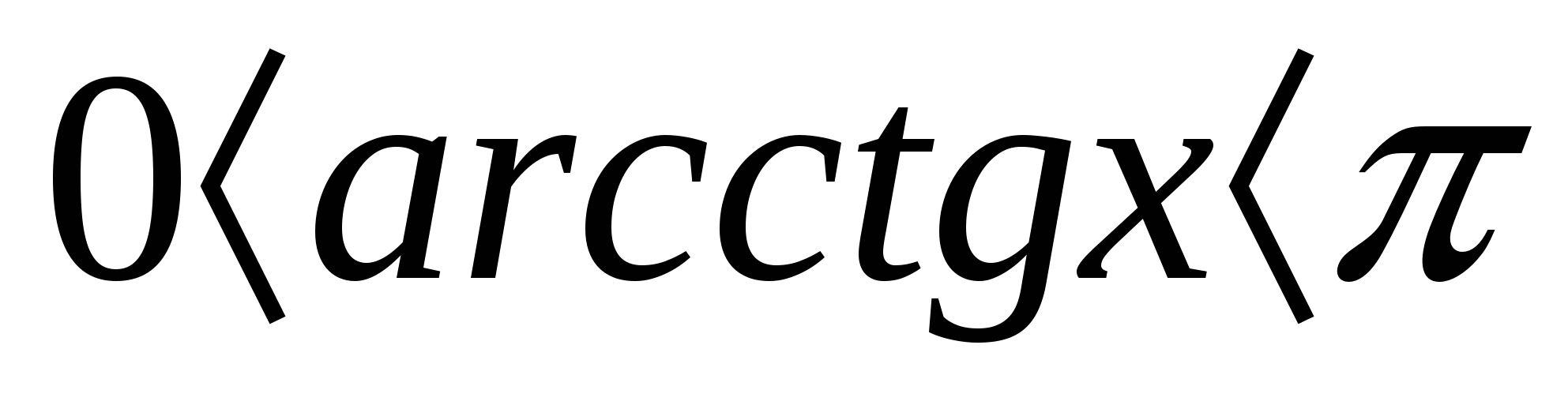 , af(x)>0, ( f(x)±g(x))2n≥0,
, af(x)>0, ( f(x)±g(x))2n≥0, ![]() , a+
, a+![]() ≥2, b+
≥2, b+![]() ≤-2 и многие другие. Здесь n-натуральное число, h(x)≥0, a>0, b0.
≤-2 и многие другие. Здесь n-натуральное число, h(x)≥0, a>0, b0.
Кроме приведённых простейших неравенств имеются и более сложные , в частности, тригонометрические неравенства -![]() ,
,
![]() ,
,
и неравенства с модулями вида ![]() .
.
Пример 1. Решить уравнение: ![]()
Решение: выделим полный квадрат в правой части уравнения, т.е. ![]() . Отсюда следует, что
. Отсюда следует, что ![]() . Так как при этом sinπx≤1, то получаем систему уравнений
. Так как при этом sinπx≤1, то получаем систему уравнений 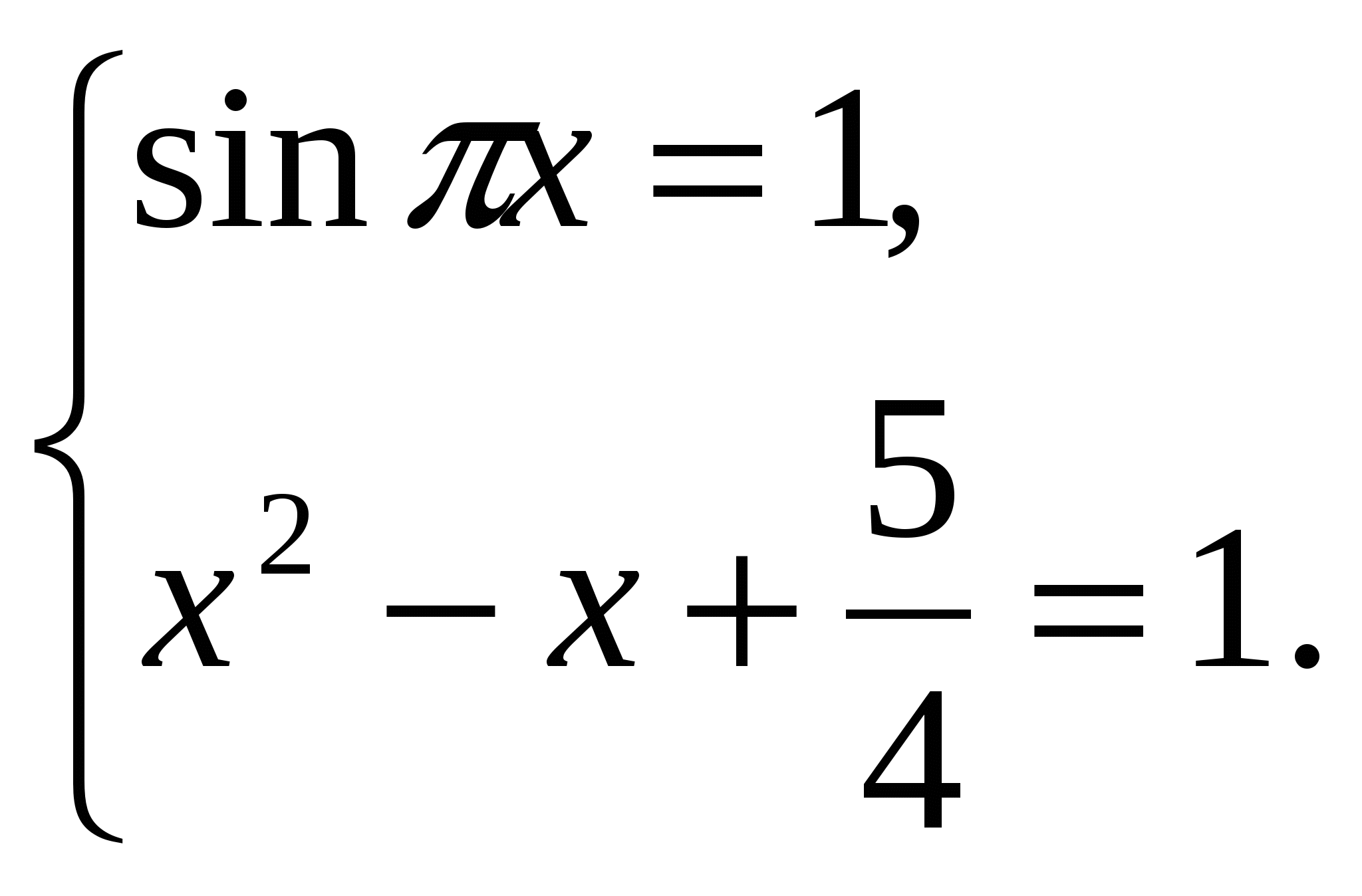
Решая второе уравнение системы, получаем что х=![]() . Подстановкой в первое уравнение убеждаемся, что найденное значение х является решением системы, а значит, является решением исходного уравнения.
. Подстановкой в первое уравнение убеждаемся, что найденное значение х является решением системы, а значит, является решением исходного уравнения.
Ответ: х=![]() .
.
Пример 2. Решить уравнение: ![]()
![]()
![]()
Решение: так как ![]() Однако sin2πx≤1. Поэтому, 5+4sin2πx≤9. Таким образом, получаем систему уравнений:
Однако sin2πx≤1. Поэтому, 5+4sin2πx≤9. Таким образом, получаем систему уравнений: 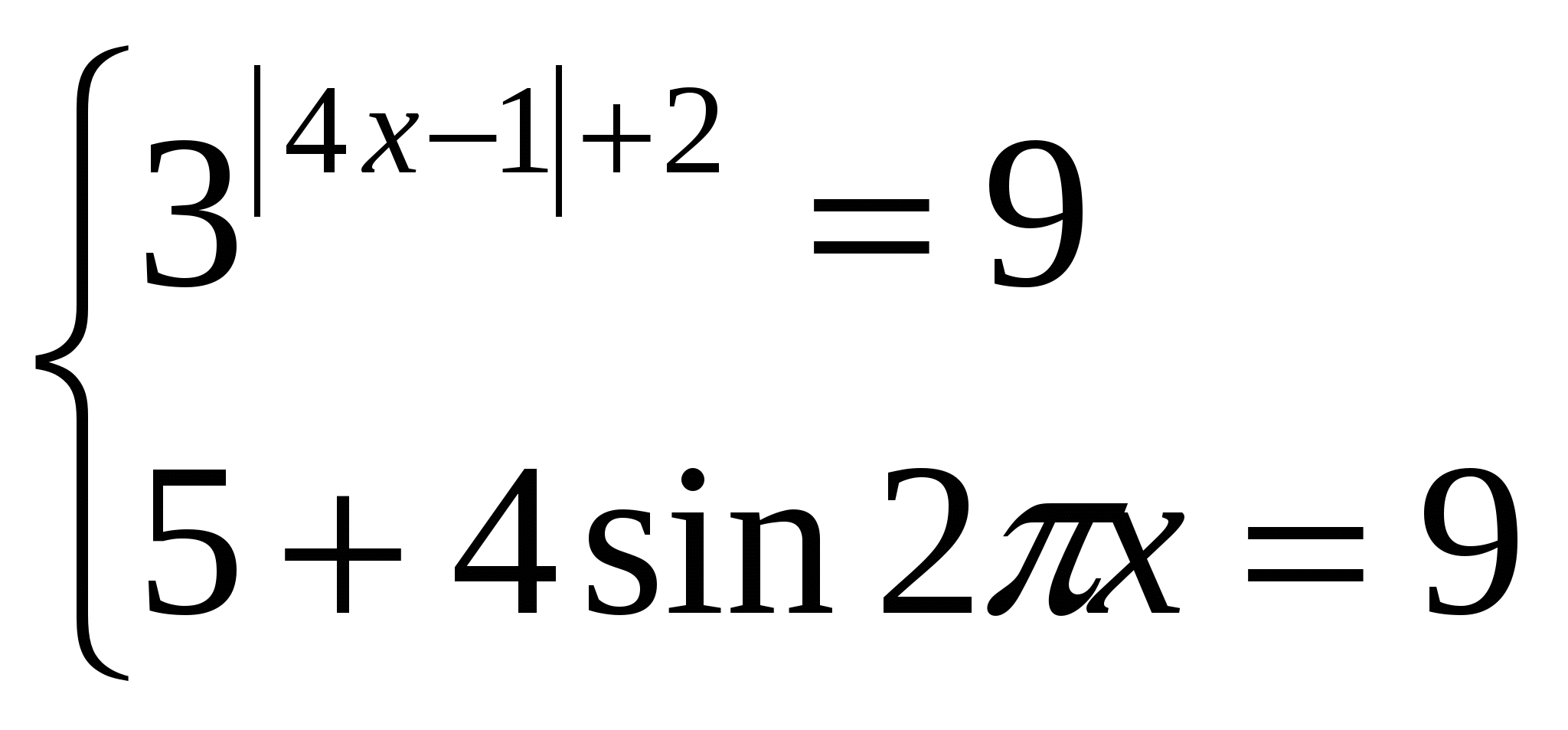
Отсюда получаем систему уравнений 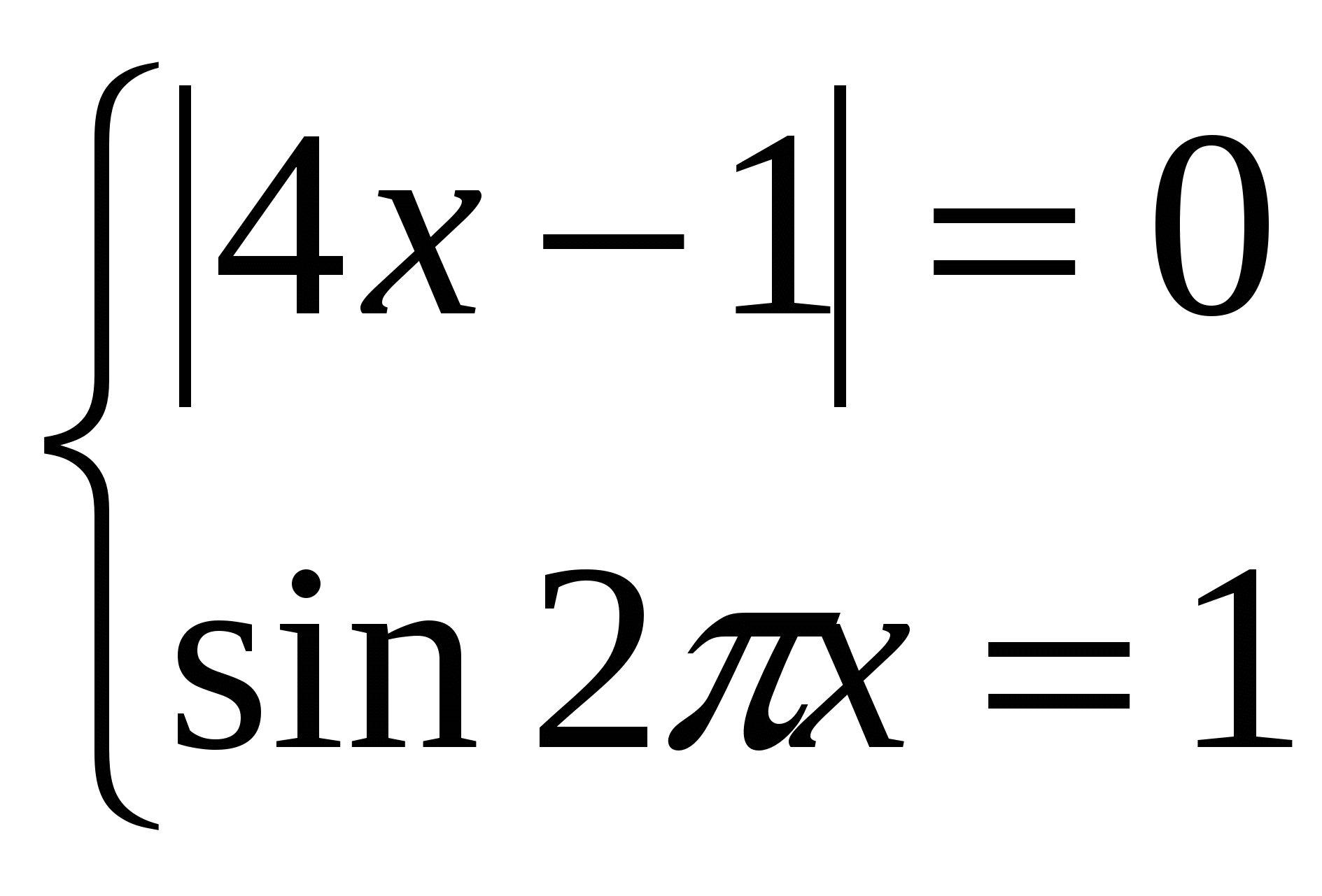 , из первого уравнения найдём х=
, из первого уравнения найдём х=![]() . Подставим его во второе уравнение системы и убедимся, что х=
. Подставим его во второе уравнение системы и убедимся, что х=![]() является решением системы, а значит, является решением исходного уравнения.
является решением системы, а значит, является решением исходного уравнения.
Ответ: х=![]()
Приложение 4.
Из предложенного списка заданий выберите те, которые можно решить и использованием метода ограниченности функций.
1. Решить уравнение х2-4x=(2-cos![]()
2. Найти количество целочисленных решений неравенства х2+7х-8≤0, удовлетворяющих условию ctg2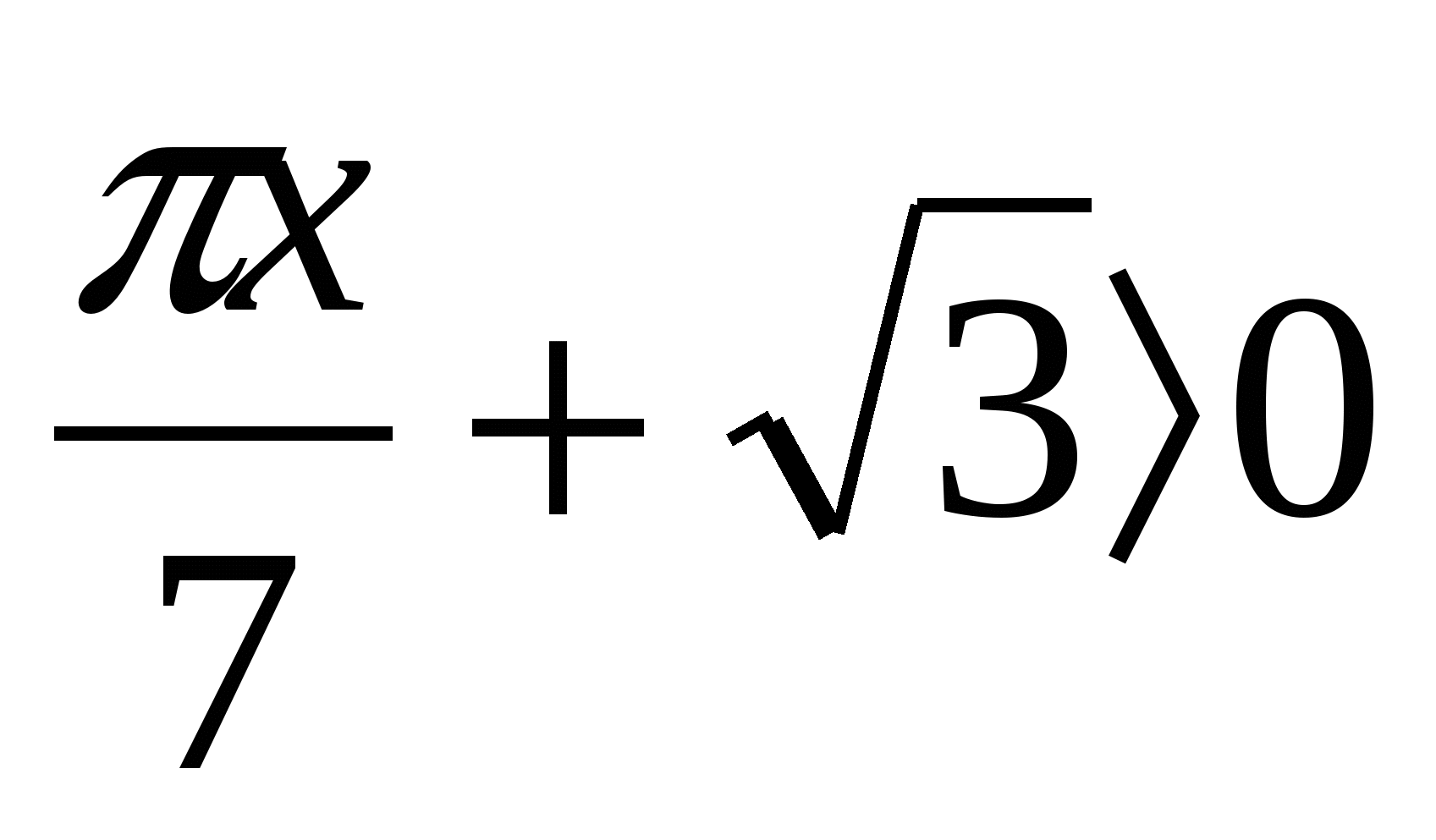
3. Решить уравнение ![]()
4. Решить уравнение 3-(![]()
5. Найти количество целочисленных решений неравенства 16-х2≥0, удовлетворяющих условию 3tg2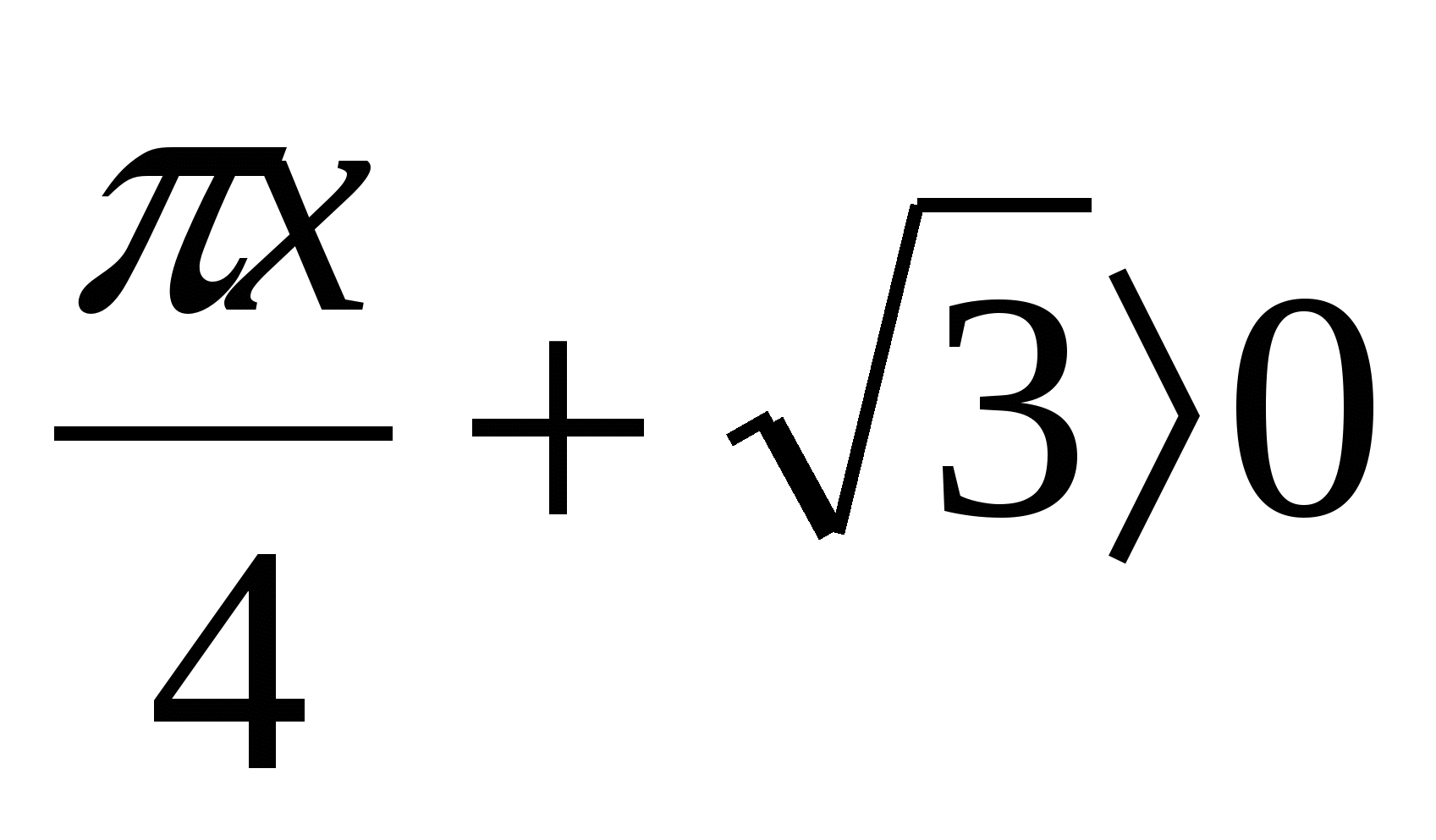
6. Решить уравнение ![]()
7. Решить уравнение -25х2+40х-23=(cos![]()
8. Найти произведение корней уравнения х![]()
9. Решить уравнение ![]()
10. Решить уравнение 3-cos2![]()
Лист самопроверки. Приложение 5.
1. Решить уравнение ![]()
Решение: т.к. , то
т.к. и , то
получаем систему уравнений
решаем первое уравнение, получаем х= , подставим это значение во второе уравнение
значит х= является решением исходного уравнения. Ответ: х=
2 . Решить уравнение 3-cos2![]()
Решение: т.к. , то
т.к. и , то
получаем систему уравнений
решаем второе уравнение, получаем х= , подставим это значение в первое уравнение
значит х= является решением исходного уравнения. Ответ: х=
3 . Найти количество целочисленных решений неравенства х2+7х-8≤0, удовлетворяющих условию ctg2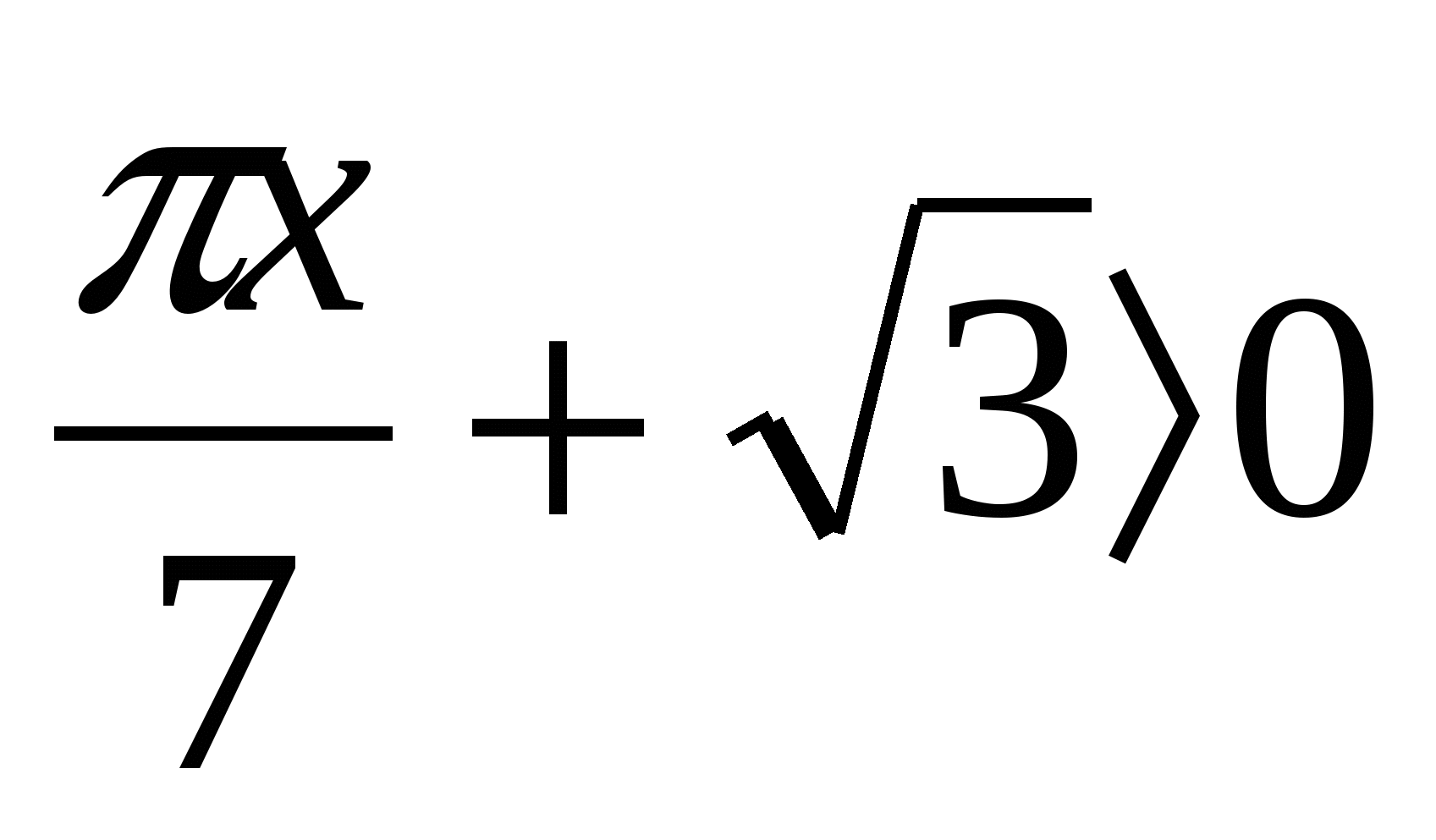
Решение: т.к. и то при любых допустимых значениях х
Найдём нули квадратного трёхчлена , по теореме Виета
Решим неравенство методом интервалов
т.о. х
знаем, что
целочисленные значения х - это числа
исключаем Ответ: 8 целочисленных решений
4 . Найти количество целочисленных решений неравенства 16-х2≥0, удовлетворяющих условию 3tg2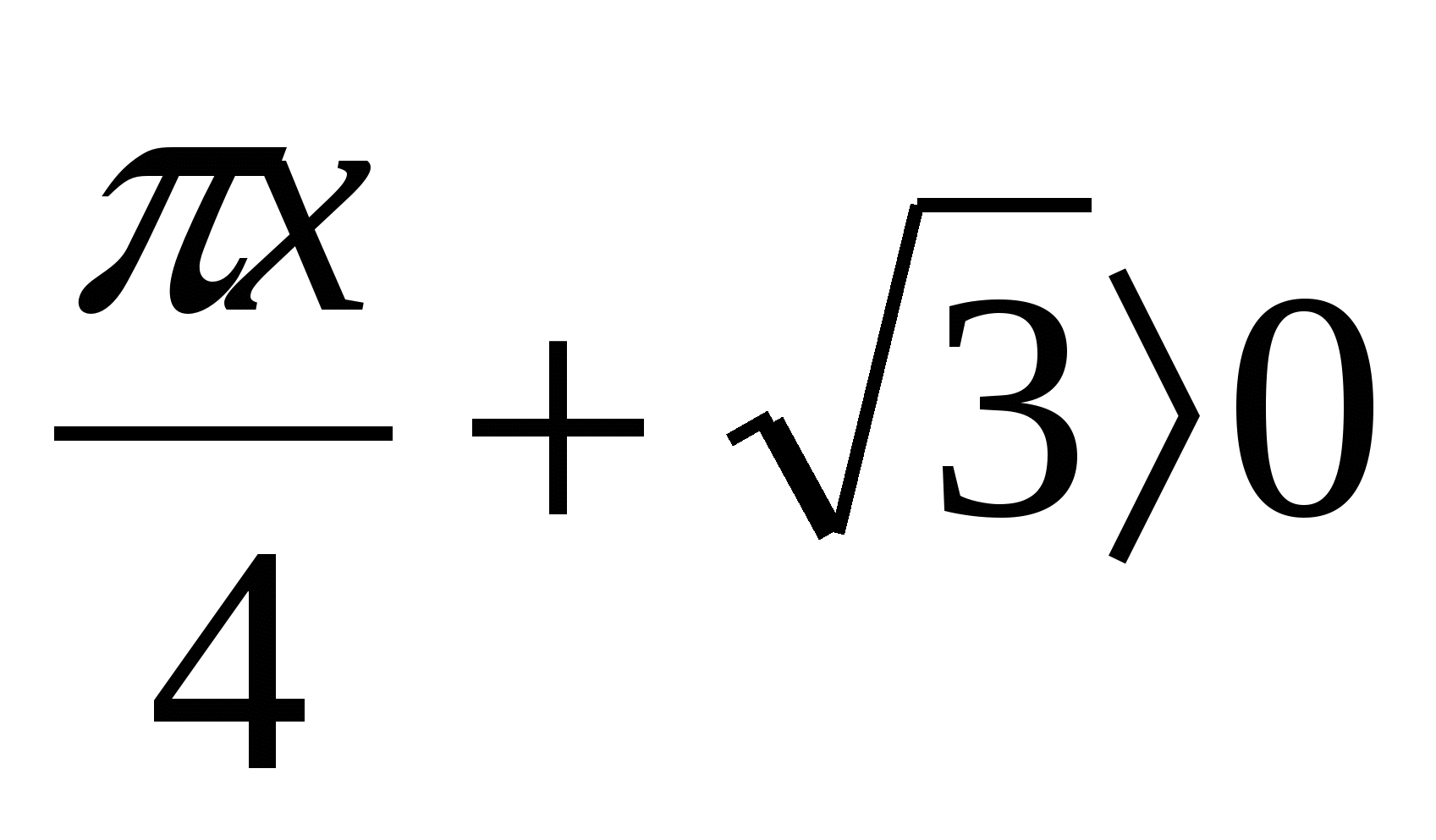
Решение: т.к. и то при любых допустимых значениях х
Найдём нули выражения , х= и х=
Решим неравенство методом интервалов
т.о. х
знаем, что
целочисленные значения х - это числа
исключаем Ответ: 7 целочисленных решений
Приложение 6.
Метод использования монотонности функций.
При решении уравнения типа f(x)=g(x) в ряде случаев эффективным является метод, который использует монотонность функций у= f(x) и у= g(x).
Если функция у= f(x) непрерывна и возрастает (убывает) на отрезке a≤x≤b, а функция у= g(x) непрерывна и убывает ( возрастает) на этом же отрезке, то уравнение f(x)=g(x) на отрезке a≤x≤b может иметь не более одного корня, значит необходимо или попытаться подбором найти единственный корень уравнения, или показать, что такого корня не существует. Особенно этот метод эффективен в том случае, когда обе части уравнения f(x)=g(x) представляют собой «неудобные» для совместного исследования функции.
Замечание: Если функция у= f(x) возрастает, а функция у= g(x) убывает для a≤x≤b и при этом f(а)>g(а), то корней уравнения среди a≤x≤b нет.
Пример: Решить уравнение ![]()
Решение: Областью допустимых значений уравнения являются х![]() . Нетрудно видеть, что на этой области левая часть уравнения возрастает, а правая - убывает, т.е. функция f(x)=
. Нетрудно видеть, что на этой области левая часть уравнения возрастает, а правая - убывает, т.е. функция f(x)=![]() является возрастающей, а функция g(x)=
является возрастающей, а функция g(x)=![]() - убывающая. В этой связи исходное уравнение может иметь только один корень ( если он есть). Подбором находим этот корень уравнения х=2.
- убывающая. В этой связи исходное уравнение может иметь только один корень ( если он есть). Подбором находим этот корень уравнения х=2.
Ответ: х=2
Метод решения функциональных уравнений.
К числу наиболее сложных задач на ЕГЭ относятся задачи, решение которых сводится к рассмотрению функциональных уравнений вида
f(f(….f(x)…))=x или f(g(x))=f(h(x)), где f(x),g(x),h(x)- некоторые функции и n≥2
Методы решения этих функциональных уравнений основаны на применении многих теорем, рассмотрим одну из них.
Теорема1. Корни уравнения f(x)=0 являются корнями уравнения f(f(….f(x)…))=x
Пример: Решить уравнение х=![]() , где квадратный корень берётся n раз и n≥1
, где квадратный корень берётся n раз и n≥1
Решение: Из условия задачи следует, что х>0. Пусть f(x)=![]() , тогда наше уравнение можно представить в виде функционального f(f(….f(x)…))=x. Так как при х>0 функция f(x)=
, тогда наше уравнение можно представить в виде функционального f(f(….f(x)…))=x. Так как при х>0 функция f(x)=![]() возрастает и f(x)>0, то уравнение х=
возрастает и f(x)>0, то уравнение х=![]() равносильно уравнению f(x)=x, т.е.
равносильно уравнению f(x)=x, т.е. ![]() =х, положительным решением которого является х=
=х, положительным решением которого является х=![]()
Ответ: х=![]()
Здесь представлен конспект к уроку на тему «Методы использования ограниченности функций», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

