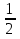Конспект урока «Типы тригонометрических уравнений и их решение» по математике


 Тема: «Типы тригонометрических уравнений и их решение»
Тема: «Типы тригонометрических уравнений и их решение»
Цели:
1.Образовательная: познакомить учащихся с типами тригонометрических уравнений и научить решать простейшие виды однородных, приводимых к алгебраическим и решаемых разложением на множители уравнений.
2. Развивающая: развивать навыки работы учащихся с дополнительным справочным материалом и таблицами тригонометрических формул.
3.Воспитательная: воспитывать познавательную активность и самостоятельность учащихся.
Тип урока: изучения нового материала
Вид урока: урок – семинар.
Форма работы: групповая
Оборудование и материалы:
-
Папка со справочным материалом и таблицами тригонометрических формул
-
Карточки-инструкции, раздаточный материал.
Ход урока
-
Организационный момент
-
Актуализация опорных знаний реализуется в форме соревнования между группами по вопросам и заданиям (табл.1).
| Вопросы для соревнования групп | № отвечающей группы | Начисленные баллы | |
| 1 | Какие уравнения называются тригонометрическими? | 1 | |
| 2 | Приведите примеры простейших ТУ | 2 | |
| 3 | Сколько корней может иметь ТУ? | 3 | |
| 4 | В уравнениях cosx=a, sinx=a оцените а | 4 | |
| 5 | Как решаются простейшие ТУ? | 5 | |
| 6 | По какой формуле находятся кони уравнения cosx=a? | 1 | |
| 7 | Соотнесите уравнения с их решениями cosx=1, cosx=-1, cosx=0 | 2 | |
| 8 | Отметить на единичной окружности точки, удовлетворяющие уравнению: cosx= - | 3 | |
| 9 | По какой формуле находятся корни уравнения sinx=a? | 4 | |
| 10 | Соотнесите уравнения с их решениями: sinx=1, sinx= -1, sinx= 0. | 5 | |
| 11 | Отметить на единичной окружности точки, удовлетворяющие уравнению sinx= | 1 | |
| 12 | По какой формуле находятся корни уравнения tgx=a | 2 | |
| 13 | По какой формуле находятся корни уравнения ctgx=a | 3 | |
| 14 | В уравнениях tgx=a, ctgx=a оцените а. | 4 | |
| 15 | Чему равен arcctg (-x) | 5 | |
| | | | |
За каждый правильный ответ группе начисляется 1 балл.
-
Объяснение нового материала.
1.Учитель знакомит учащихся с типами уравнений-однородные, приводимые к алгебраическим и решаемые разложением на множители (табл.1)
ТРИГОНОМЕТРИЧЕСКИЕУРАВНЕНИЯ
однородные приводимые к алгебраическим решаемые разложением
на множители
-
а).Решение алгебраических уравнений заключается в том, что все тригонометрические функции, которые входят в уравнение, выражают через какую-нибудь одну тригонометрическую функцию, зависящую от одного и того же аргумента.
Пример. 2sin2 2x + 5 sin2x – 3 = 0
б) Решение однородных уравнений (уравнения, в которых у всех слагаемых сумма показателей одинакова) и приводимых к ним сводится к решению алгебраических относительно tgx путём деления обеих частей уравнения на cosx≠0 и cos2 x≠0 соответственно.
Пример. 1 – 3sinx*cosx – 5cos2x = 0
в) Решение с помощью разложения на множители сводится к решению двух элементарных уравнений.
Пример. 2cosx-4cosxsinx=0
-
Работа в группах.
Закрепление реализуется по РМ 1
Задание №1
Назовите тип уравнений
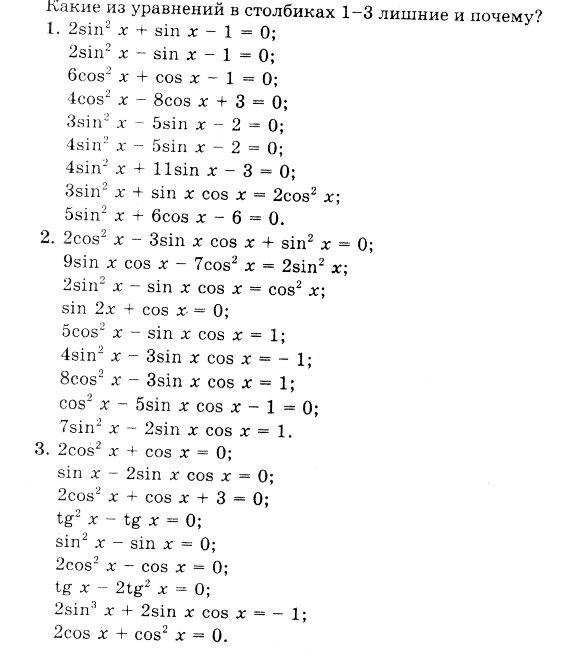
Каждая группа получает карточку-инструкцию для самостоятельного решения одного из типов уравнений. Учащимся необходимо выбрать из предложенных уравнений два уравнения указанного в задании типа и решить их, используя карточку-инструкцию.
Задание №2
I, III группа
Решение однородных уравнений (уравнения, в которых у всех слагаемых сумма показателей одинакова) и приводимых к ним сводится к решению алгебраических относительно tgx, путём деления обеих частей уравнения на cosx≠0 и cos2 x≠0 соответственно.
Алгоритм
решения однородного уравнения
1. Приведение к однородному уравнению.
2. Деление левой и правой части на Cos2x при условии Cosx![]() 0.
0.
3. Решение квадратного уравнения.
4. Подстановка.
5. Решение простейших тригонометрических уравнений.
Из предложенных уравнений выбрать три однородных и решить их, используя алгоритм.
Задание №2
II, IV группа
Решение алгебраических уравнений заключается в том, что все тригонометрические функции, которые входят в уравнение, выражают через какую-нибудь одну тригонометрическую функцию, зависящую от одного и того же аргумента.
Алгоритм
решения уравнения сводящегося к алгебраическому
1. Замена переменной.
2. Решение квадратного уравнения.
3. Решение простейших тригонометрических уравнений.
Из предложенных уравнений выбрать три сводящихся к алгебраическим и решить их, используя алгоритм.
Задание №2
III группа
Решение уравнений с помощью разложения на множители сводится к решению двух элементарных уравнений.
Алгоритм
решения уравнений с помощью разложения на множители
-
Разложить на множители любым известным способом
-
Приравнять каждый сомножитель к нулю на основании теоремы : «Произведение рано 0, тогда и только тогда. Когда один из сомножителей равен 0, а другой при этом не теряет смысла»
-
Решить получившиеся элементарные уравнения.
Из предложенных уравнений выбрать три решаемых разложением на множители и решить их, используя алгоритм.
-
Отчет групп о выполненной работе .
К доске вызываются по одному учащемуся от группы с решенным уравнением указанного типа. Остальные учащиеся слушают, комментируют, задают вопросы.
-
Итоги урока. Подсчитываются набранные баллы, выставляются оценки.
-
Домашнее задание. Решить по три уравнения разного типа из РМ.
Здесь представлен конспект к уроку на тему «Типы тригонометрических уравнений и их решение», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.