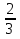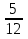Конспект урока «Применение производной к исследованию функции» по алгебре для 11 класса


 Урок 49
Урок 49
Тема урока: «Применение производной к исследованию функции»
Предмет: Алгебра и начала анализа
Тип занятия: закрепления изученного материала
Класс: 11
УМК: Колмогоров А.Н. Алгебра и начала анализа. 2006 год.
Учитель математики: Дерюгина Дарья Ивановна.
Должность: учитель математики
Место работы: Муниципальное общеобразовательное бюджетное учреждение средняя общеобразовательная школа № 21 Краснодарского края, Лабинского района, станицы Ахметовской.
Цели урока: учить применять производную для исследования функций и построения графиков.
образовательные
- применение полученных теоретических знаний по теме: «Производная» при решения упражнений;
- применение схемы исследования функции;
- продолжить подготовку к ЕГЭ и КДР по математике;
воспитательные
- воспитание культуры общения, взаимопомощи, умение слушать товарища;
- воспитание потребности в знаниях;
- воспитание навыков умственного труда;
развивающие
- развитие творческой стороны мышления;
- умение осуществлять исследовательскую деятельность.
Ход урока
1.Организационный момент
2.Сообщение темы и целей урока
3.Актуализация опорных знаний
1.Устная работа
- В чем состоит геометрический смысл производной?
- Что такое экстремумы функции; максимумы; минимумы?
- Сформулируйте достаточный признак убывания и возрастания функции.
- Расскажите, как найти наибольшее (наименьшее) значения функции на отрезке [а;b].
2.Фронтальная работа
Выполнение заданий 1-11 (задания В8 ЕГЭ по математике).
На рисунке изображен график производной функции у =f (x), заданной на промежутке (- 8; 8). Исследуя свойства графика, мы можем ответить на множество вопросов о свойствах функции, хотя графика самой функции не представлено!
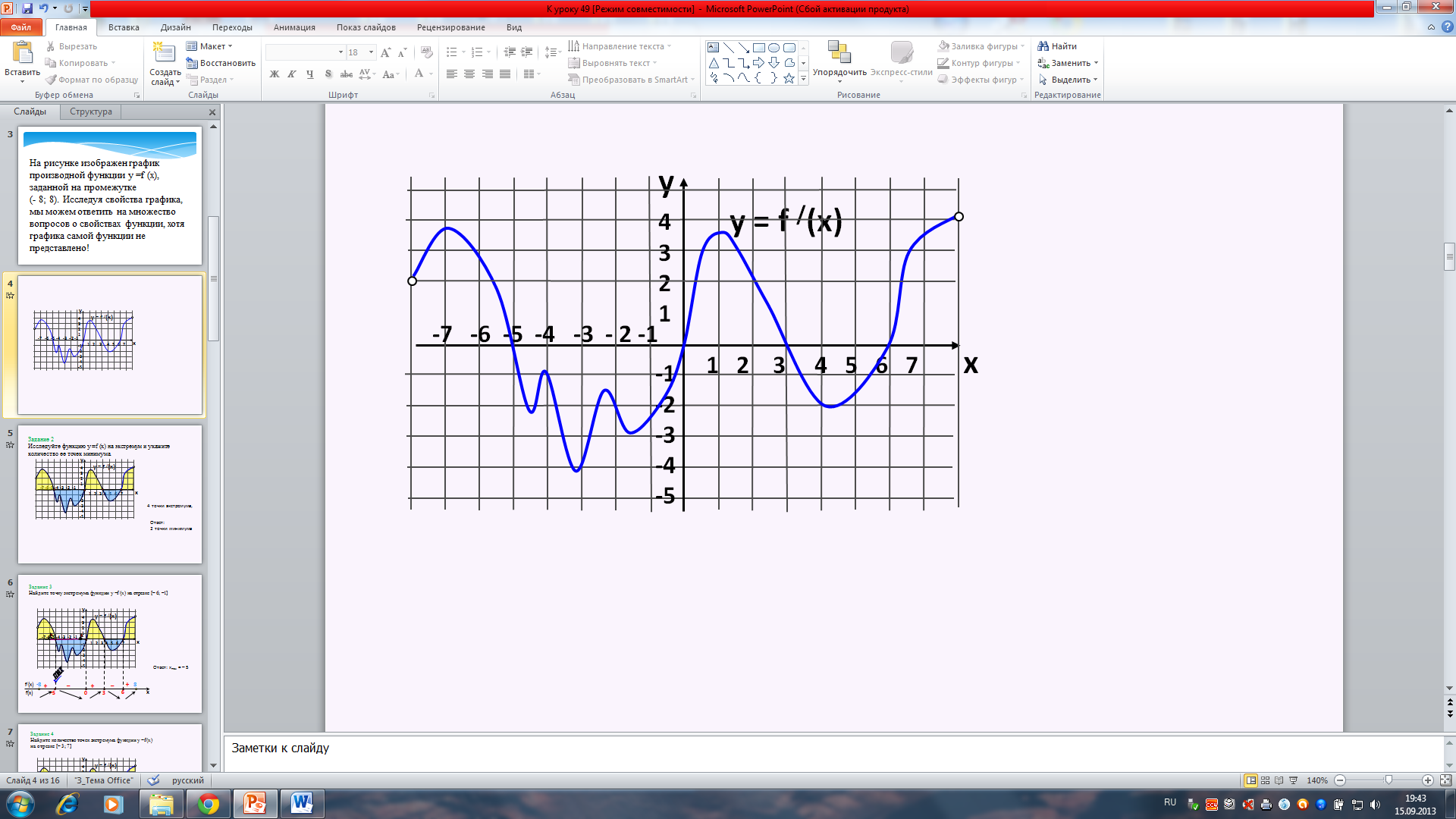
Задание 1. Найдем точки, в которых f /(x)=0.
Задание 2. Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума.
Задание 3. Найдите точку экстремума функции у =f (x) на отрезке [– 6; –1].
Задание 4. Найдите количество точек экстремума функции у =f (x)
на отрезке [– 3; 7]
Задание 5. Найдите промежутки возрастания функции у =f (x).
Задание 6. Найдите промежутки возрастания функции у =f (x). В ответе укажите сумму целых точек, входящих в эти промежутки.
Задание 7. Найдите промежутки убывания функции у =f (x). В ответе укажите длину наибольшего из них.
Задание 8. В какой точке отрезка [– 4; –1] функции у =f (x) принимает наибольшее значение?
Задание 9 . В какой точке отрезка [– 4; –1] функции у =f (x) принимает наименьшее значение?
Задание 10. В какой точке отрезка [ 0; 3] функции у =f (x) принимает наибольшее значение?
Задание 11. В какой точке отрезка [1; 4] функции у =f (x) принимает наибольшее значение?
4. Работа по теме урока. Решение упражнений
1.Назовите схему исследования функции с применением производной
2.Решение упражнения из учебника А.Н.Колмогорова «Алгебра и начала анализа»
а) № 10 (2, в) страница 172
Исследуем функцию:
- найдем критические точки
- найдем промежутки возрастания и убывания функции ;
- найдем максимумы и минимумы функции;
- найдем значения функции в критических точках;
- найдем область определения функции;
- определим четность (нечетность) функции.
Заполним таблицу:
| ( | - 2 | (- 2; 0) | 0 | (0; 1) | 1 | (1; + | |
| f /(x) | - | 0 | + | 0 | - | 0 | + |
| f (x) | | - 2 | | 0 | | - | |
| | | min | | max | | min | |
б) Более подготовленные учащиеся выполняют № 10 (3, г) страница 172.
2.Работа со слабоуспевающими учащимися
Выполнение заданий карточки (подготовка к ЕГЭ по математике)
Карточка 1
В1. Поезд Самара-Волгоград отправляется в 19:54 , а прибывает в 12:24 следующего дня (время московское). Сколько часов поезд находится в пути?
В2. На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией.
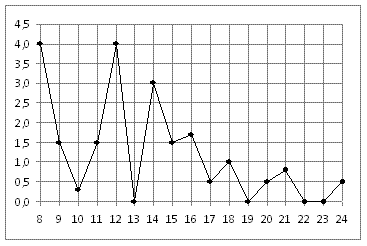
Определите по рисунку, сколько дней не выпадало осадков.
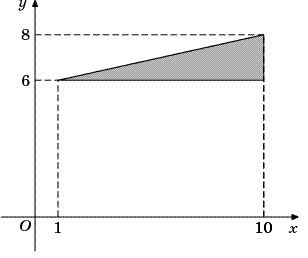
В3.Найдите площадь треугольника, вершины которого имеют координаты (1;6), (10;6), (10;8) .
В4. В таблице указаны средние цены на некоторые основные продукты питания в трех городах России (по данным некоторого исследования).
| Средняя цена (в рублях) | |||
| Кострома | Тамбов | Хабаровск | |
| Пшеничный хлеб (батон) | 11 | 14 | 12 |
| Молоко (1 литр) | 26 | 23 | 25 |
| Картофель (1 кг) | 17 | 11 | 14 |
| Сыр (1 кг) | 240 | 215 | 260 |
| Мясо (говядина) (1 кг) | 285 | 235 | 260 |
| Подсолнечное масло (1 литр) | 52 | 60 | 65 |
Определите, в каком из этих трех городов окажется самым дешевым следующий набор продуктов: - 2 батона пшеничного хлеба; - 2 л молока; - 1 кг сыра. В ответ запишите полученную сумму в рублях.
В5. Решите уравнение: 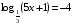
3. Проверка упражнения № 10 (3, г) страница 172
5. Подведение итогов урока
- Под каким номером тема «Производная» находится в ЕГЭ по математике?
- В чем состоит геометрический смысл производной?
6. Домашнее задание
I (слабоуспевающим учащимся): вариант 5 (КДР январь – 2012),
№ 7 (1; 3(а; в)) страница 172;
II (подготовленным учащимся): № 10(3, б), №11 (2, а; б) страница 172 – 173.
Здесь представлен конспект к уроку на тему «Применение производной к исследованию функции», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (11 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

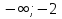 )
)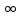 )
)