Конспект урока «ПРИЕМЫ УСТНОГО РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ» по алгебре
Федеральное государственное казенное
общеобразовательное учреждение
«Средняя общеобразовательная школа №151»
ПРИЕМЫ
УСТНОГО РЕШЕНИЯ
КВАДРАТНЫХ УРАВНЕНИЙ
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений и неравенств.
Одна из основных целей изучения школьного курса математики заключается в овладении способами решения алгебраических уравнений второй степени и приводимых к ним уравнений. В школьном курсе изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения. Желательно научить ребят решать квадратные уравнения несколькими способами. Впоследствии при решении других видов уравнений, сводящихся к квадратным, рационально использовать те способы, которые позволяют находить корни квадратных уравнений устно: свойства коэффициентов и способ «переброски» старшего коэффициента.
Данные приемы устного решения квадратных уравнений заслуживают внимания, поскольку не отражены в школьном учебнике математики. Овладение приемами поможет обучающимся экономить время, эффективно решать уравнения, развить математические, интеллектуальные способности, навыки исследовательской работы.
Рассмотрим некоторые приемы устного решения квадратных уравнений.
-
Приведенные квадратные уравнения.
Наиболее распространенное устное решение приведенных квадратных уравнений, но и оно у многих учеников вызывает затруднение, особенно в случаях, когда корни имеют разные знаки.
Напомним, что приведенное квадратное уравнение это уравнение вида
х2 + рх + q = 0
Корни х1 и х2 удовлетворяют теореме Виета
х1 х2 = q х1 + х2 = - р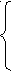
Определить знаки корней без решения уравнения (при условии, D0)
можно по следующим правилам:
| р 0 | р 0 | |
| q 0 | оба корня отрицательны | оба корня положительны |
| q 0 | корни имеют противоположные знаки | |
Рассмотрим случаи.
-
q 0
Если в уравнении х2 + рх + q = 0 q 0 ( или последним знаком является знак «минус»), то корни имеют разные знаки, причем знак меньшего корня совпадает со знаком второго коэффициента в уравнении ( будем называть его в дальнейшем вторым знаком уравнения, а числа р и q будем называть модули коэффициентов).
Зная, что при сложении чисел с разными знаками их модули вычитаются, сформулируем правило нахождения корней уравнения.
-
найти такие множители числа q, чтобы их разность была равна числу р;
-
поставить перед меньшим из найденных чисел второй знак уравнения, другой корень будет иметь противоположный знак.
Пример 1.Решить уравнение х2 – 2х – 15 = 0
Решение.
1) Найдем множители числа 15: 1 и 15, 3 и 5. Выберем те, разность которых равна 2. Это числа 3 и 5.
2)Перед меньшим числом ставим второй знак уравнения, т.е. «минус».
Таким образом, корни уравнения: х1 = - 3, х2 = 5.
Ответ: -3 и 5.
Пример 2. Решить уравнение х2 + 10х – 24 = 0
Решение.
Множители числа 24: 1 и 24; 2 и 12; 3 и 8; 4 и 6 .
10 = 12 - 2 и второй знак уравнения «+» , то х1= 2, х2 = - 12
Ответ: - 12; 2.
Пример 3. Решить уравнение х2 – 5х – 14 = 0.
Решение.
14 = 2 7 и 5 = 7 – 2, то х1 = - 2, х2 = 7.
Ответ: - 2; 7.
Такой алгоритм помогает быстро решать уравнения тем обучающимся, у которых имеются трудности с подбором знаков в теореме Виета.
Задания для самостоятельного решения.
-
Решите уравнения:
-
х2 – 4х – 77 = 0 3) х2 + х – 56 = 0
-
х2 + 8х – 20 = 0 4) х2 – 7х – 8 = 0
-
Составьте уравнение, корнями которого являются числа:
-
6 и - 7 3) - 1 и 24
-
13 и – 9 4) - 5 и 4
-
Составьте четыре произвольных уравнения с целыми корнями, имеющими разные знаки.
-
q 0
Если в уравнении х2 + рх + q = 0 q 0 (или последним знаком является знак «плюс») то уравнение имеет два корня и оба корня имеют одинаковые знаки, противоположные второму знаку уравнения.
Сформулируем правило нахождения корней.
-
если в уравнении два знака «плюс», то оба корня имеют знак «минус»;
-
чтобы найти корни, нужно найти такие множители свободного члена q, чтобы их сумма была равна числу р.
Пример 1. Решить уравнение х2 + 7х + 12 = 0.
Решение.
12 = 1 12 = 2 6 = 3 4 и 3 + 4 = 7, а в уравнении два «плюса»,
то корни уравнения х1 = -3, х2 = -4.
Ответ: х1 = -3, х2 = -4.
Пример 2. Решить уравнение х2 – 9х + 14 = 0.
Решение.
14 = 2 7 и 2 + 7 = 9, второй знак «минус», последний знак «плюс»,
значит, корни уравнения х1 = 2, х2 = 7.
Ответ: х1 = 2, х2 = 7.
Задания для самостоятельного решения.
-
Решите уравнения:
-
х2 –11х + 24 = 0 3) х2 – 17х + 30 = 0
-
х2 + 4х + 3 = 0 4) х2 + 9х + 14 = 0
-
Составьте уравнение, корнями которого являются числа:
-
5 и 7 3) 11 и 8
-
- 1 и – 6 4) - 4 и - 20
Таким образом, для нахождения корней приведенного квадратного уравнения
х2 + рх + q = 0 можно применить следующий алгоритм.
-
Найти множители свободного члена, для которых действие, указанное последним знаком уравнения, дает второй коэффициент;
2. расставить знаки у найденных множителей по следующему правилу:
-
если в уравнении два «плюса», то в ответе два «минуса»,
-
если последний знак уравнения «минус», то меньшему корню присваивается второй знак уравнения, больший корень имеет противоположный знак.
Пример 1. Решить уравнение х2 – 7х – 30 = 0.
Решение.
Множители числа 30: 1 и 30; 2 и 15; 3 и 10; 5 и 6.
Последний знак « - », подбираем те, разность которых равна 7. Это 3 и 10. Меньшему числу присваиваем знак « - ».
Таким образом, корни уравнения: х1 = -3 , х2 = 10.
Ответ: х1 = -3 , х2 = 10.
Пример 2. Решить уравнение х2 – 7х + 6 = 0.
Решение.
Среди множителей числа 6 ищем такие, сумма которых равна 7
(последний знак уравнения « + »). Это числа 1 и 6., таким образом, х1 = 1, х2 = 6.
Ответ: х1 = 1, х2 = 6.
-
Квадратные уравнения вида ax2 + bx + c = 0, a 0.
Свойства коэффициентов квадратного уравнения.
-
Пусть дано квадратное уравнение ax2 + bx + c = 0, a 0.
Если а + b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1, ![]() - корни этого уравнения.
- корни этого уравнения.
Доказательство:
Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение ![]()
Согласно теореме Виета 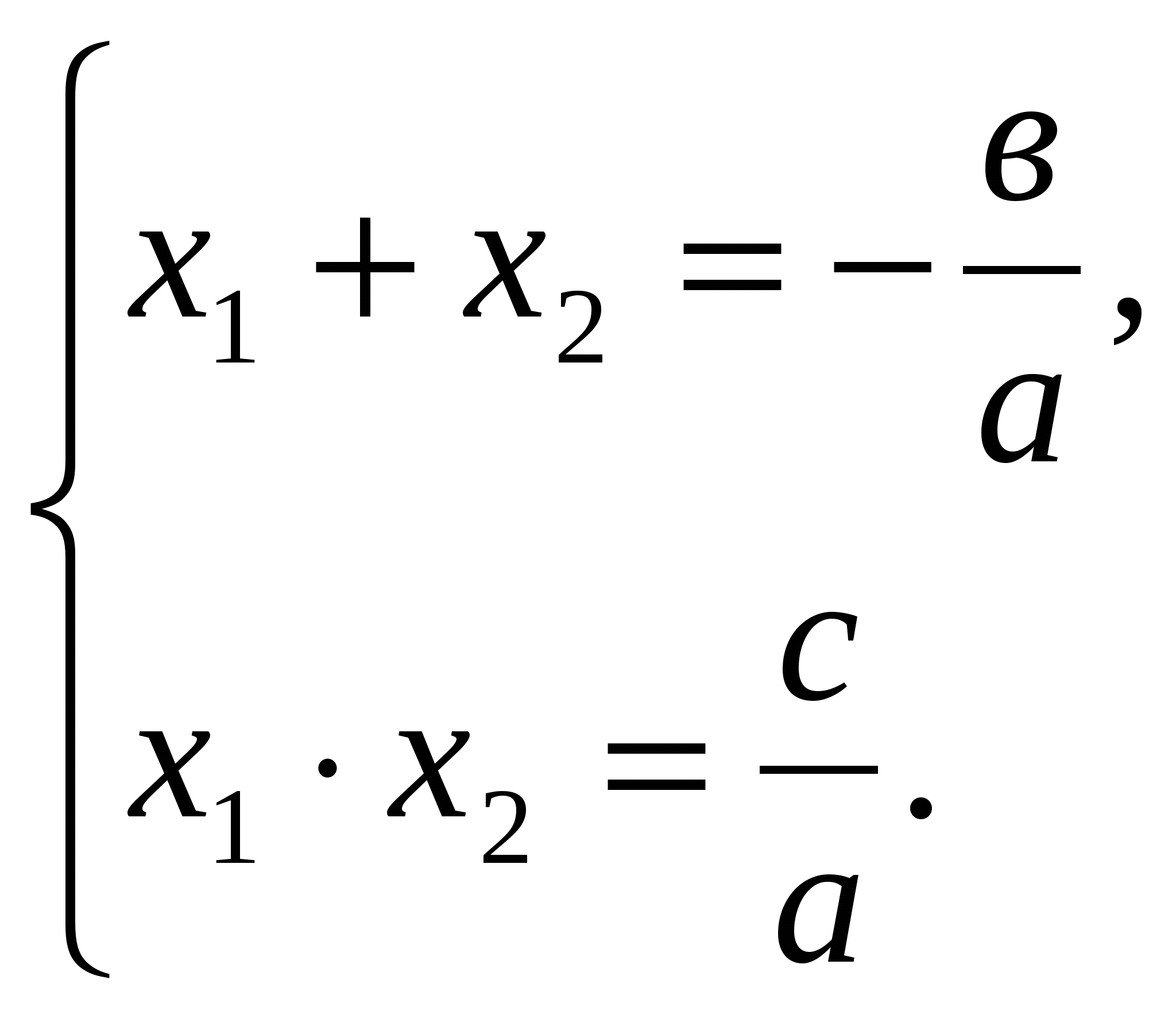
По условию а + в + с = 0, откуда в = - а – с. Значит, 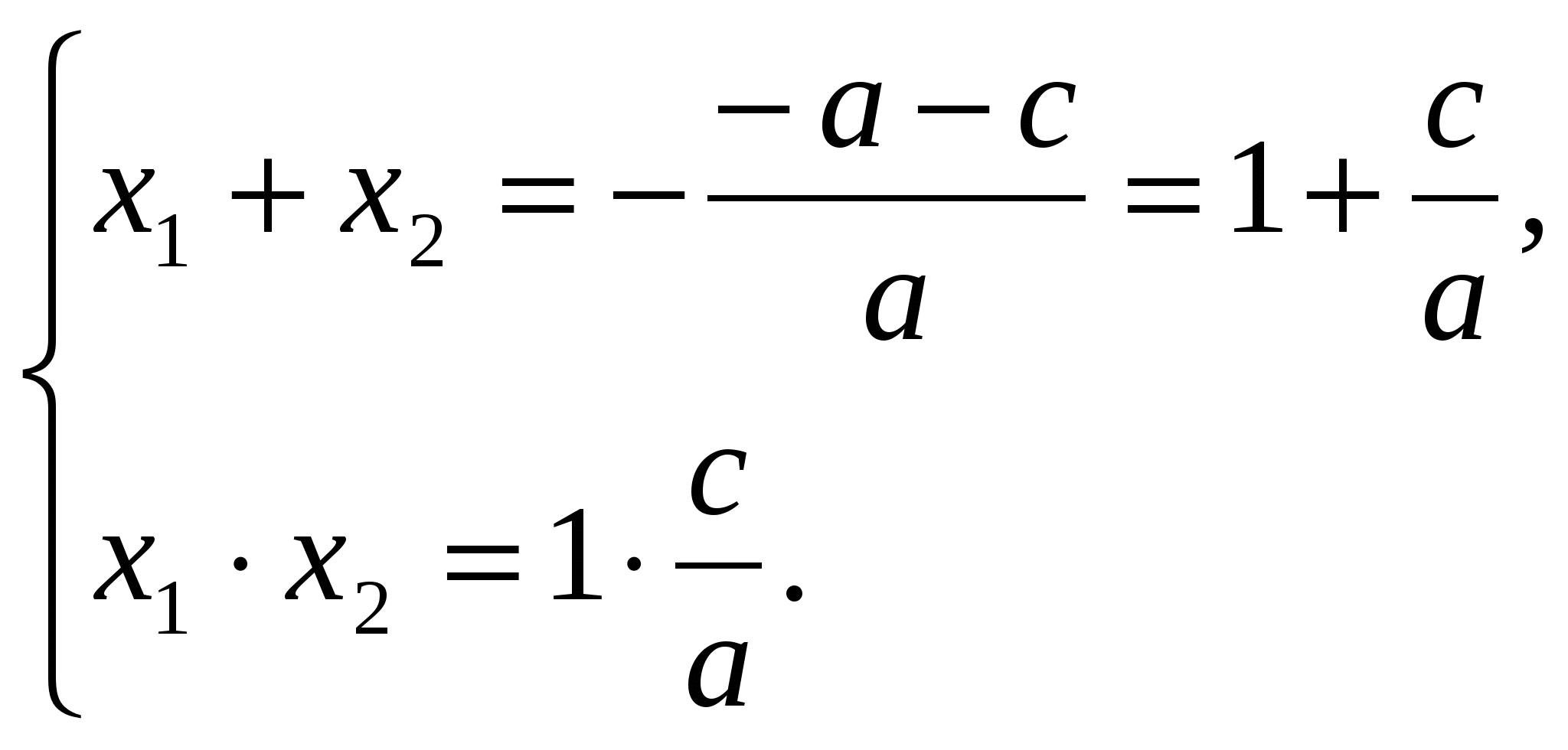
Получаем: ![]() что и требовалось доказать.
что и требовалось доказать.
2. Если а – в + с = 0, или в = а + с, то ![]()
Доказательство:
По теореме Виета 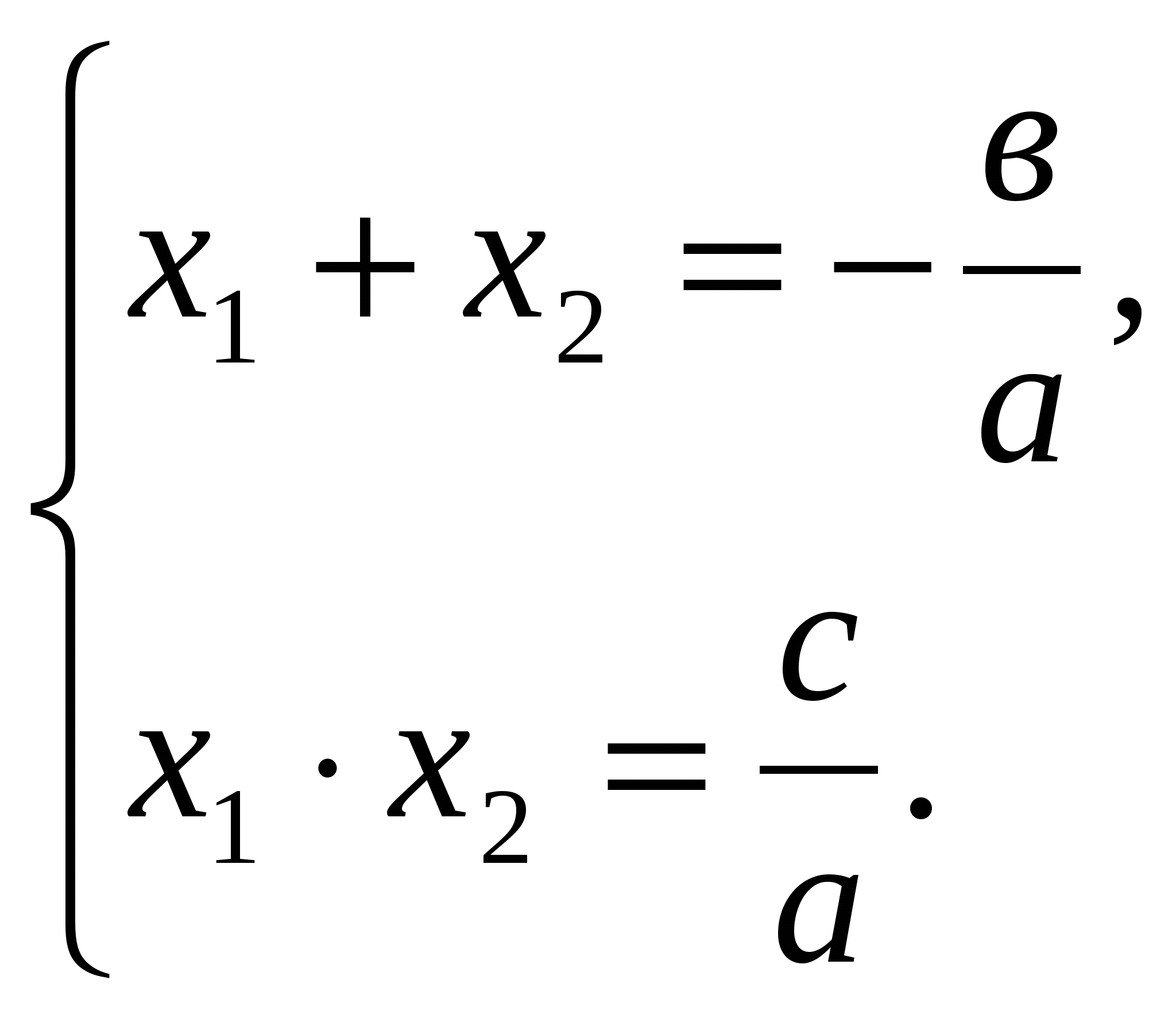
По условию а – в + с = 0, откуда в = а + с. Таким образом, 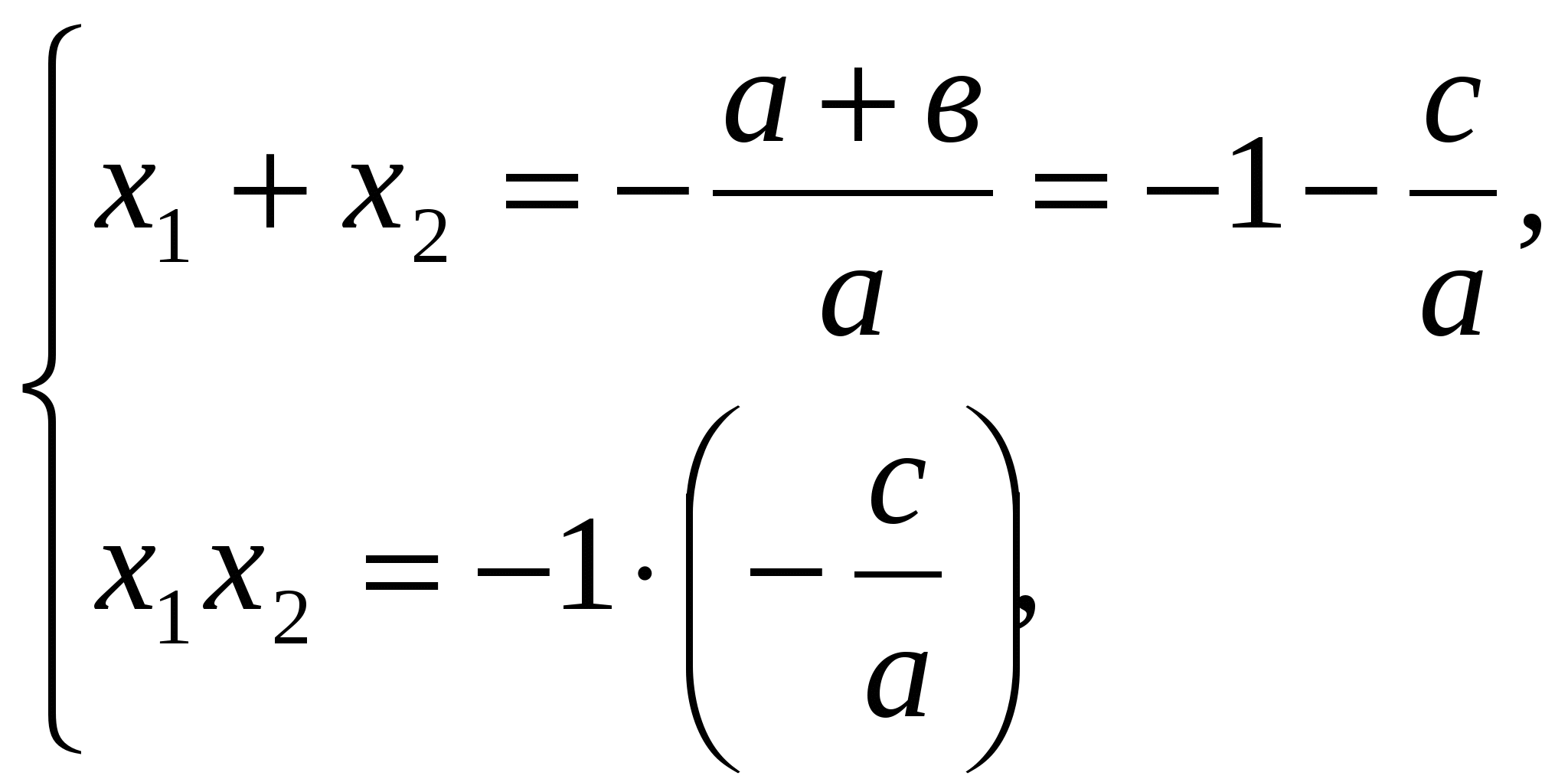
т.е. ![]() что и требовалось доказать.
что и требовалось доказать.
Из свойства коэффициентов следуют приемы устного решения квадратного уравнения – приемы «коэффициентов».
Прием 1. Если а + b + с = 0, то ![]()
Пример 1. Решить уравнение 4х2 – 13х + 9 = 0.
Решение.
Сумма коэффициентов 4 – 13 + 9 = 0, значит, ![]() - корни уравнения. Ответ:
- корни уравнения. Ответ: ![]() .
.
Пример 2. Решить уравнение ![]() = 0.
= 0.
Решение.
Сумма коэффициентов 839 – 448 – 391 = 0 , значит, ![]()
Прием 2. Если b = а + с, то ![]()
Пример 1. Решить уравнение ![]()
Решение.
7 = 2 + 5, значит, ![]() - корни уравнения
- корни уравнения
Ответ: ![]()
Пример 2. Решить уравнение 5х2 + 3х -2 = 0
Решение.
3 = 5 + (-2), значит,![]() .
.
Ответ: ![]()
Решение уравнений способом «переброски».
Если а ± b + с 0, используем метод «переброски коэффициента».
Решим уравнение ![]() Умножим обе части уравнения на a0, получим
Умножим обе части уравнения на a0, получим ![]() Пусть
Пусть ![]() , откуда
, откуда ![]()
Тогда приходим к уравнению, равносильному данному ![]() Его корни у1 и у2 .
Его корни у1 и у2 .
Окончательно ![]() .
.
При этом способе коэффициент a умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Пример 1.Решить уравнение 3х2 + 2х – 1 = 0
Решение.
3х2 + 2х – 1 = 0, | 3
9х2+ 6х – 3 = 0
(3х )2 + 2 (3х) – 3 = 0
Пусть 3х = у, тогда получим уравнение: у2 + 2у – 3 = 0. Сумма коэффициентов равна нулю: 1 + 2 + 3 = 0, значит, у1 = 1, у2= -3/ 1 = -3.
Вернемся к подстановке: 1) 3х = 1, х = 1/ 3.
2) 3х = - 3, х = - 1.
Ответ: х1 = - 1, х2 = 1/3.
Р ешение может быть таким:
ешение может быть таким:
П ример 2. Решить уравнение 2х2 – 11х + 5 = 0
ример 2. Решить уравнение 2х2 – 11х + 5 = 0
Решение.
«Перебросив» коэффициент, получим приведенное квадратное уравнение
х2 - 11 х + 10 = 0, корни которого 1 и 10. Делим каждое число на 2, получаем корни данного уравнения: х1 = 0,5, х2 = 5.
Пример 3. Решить уравнение 6х2 – 7х – 3 = 0.
Решение.
«Перебросив» коэффициент, получим приведенное квадратное уравнение
х2 – 7х – 18 = 0, корни которого 9 и – 2.
Делим на ![]() ,
, ![]() - корни данного уравнения
- корни данного уравнения
 Ответ:
Ответ: ![]() .
.
Пример 4. Решить уравнение ![]()
Решение:
Используя метод «переброски», получим уравнение
![]()
По теореме Виета 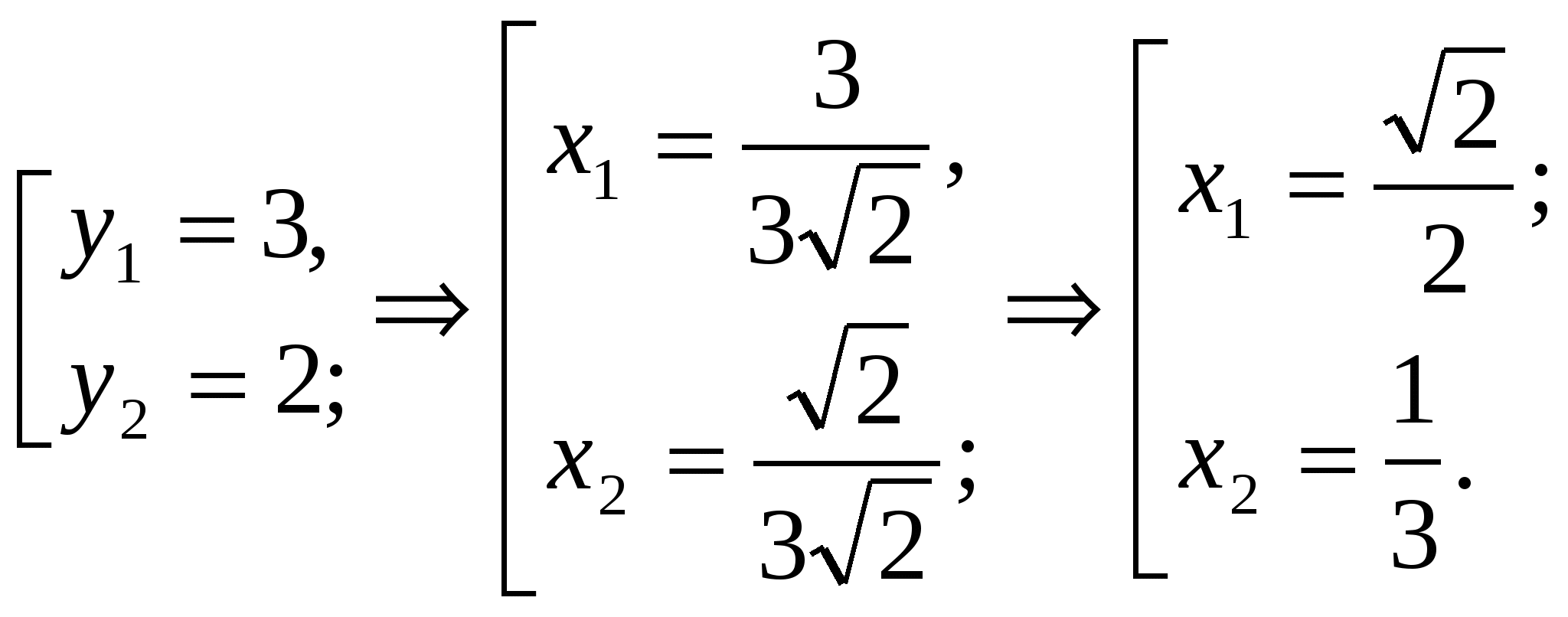
Ответ: ![]()
Задания для самостоятельного решения.
Решить уравнения:
-
5х2 - 7х +2 =0 1) 5х2 - 7х -12 =0
-
11х2 +25х - 36=0 2) 11х2 +25х +14=0
-
345х2 -137х -208=0 3) 3х2 +5х +2=0
-
3х2 +5х - 8=0 4) 5х2 + 4х - 1=0
-
5х2 + 4х - 9=0 5) х2 + 4х +3=0
-
2х2 -9х +9=0
-
10х2 -11х + 3=0
-
3х2 +11х +6=0
-
6х2 +5х - 6=0
-
3х2 +1х - 4=0
Литература.
-
Мордкович А. Г.. Алгебра 8 кл. Учебник для общеобразовательных учреждений.// М. Мнемозина.- 2012 г.
-
Плужников И. Г. « 10 способов решения квадратных уравнений» //Математика в школе.-2000.- № 40.
-
Михайлова Ж. Н. Алгоритмы – ключ к решению задач по алгебре. Ч 1.// М. Просвещение.-2008г.
Здесь представлен конспект к уроку на тему «ПРИЕМЫ УСТНОГО РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

