Тест по информатике для 7 класса














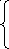 Тест по информатике для 7 класса
Тест по информатике для 7 класса
1. В каком году появился термин “Линейное программирование”?
-
1935;
-
1951;
-
1899;
-
1962;
-
1901.
2. Кто из нижеперичисленных учёных провёл первые исследования в области математического программирования?
-
Канторович;
-
Лейбниц
-
Ломоносов
-
Лебедев
-
Паскаль
3. Исследованием каких задач занимается математическое программирование?
-
задач, в которых из множества возможных решений требуется выбрать наилучшее (оптимальное);
-
задач, в которых из множества возможных решений требуется выбрать наихудшее;
-
задач, в которых из множества возможных решений требуется выбрать нулевое;
-
верны A) и B);
-
нет верного.
4. Выберите неправильный вариант синонимов математического программирования.
-
математическое планирование;
-
оптимальное планирование;
-
математическое прогнозирование;
-
оптимальное программирование;
-
нет правильного.
5. Как называется область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума или минимума) линейной функции многих переменных при наличии линейных ограничений, т. е. равенств или неравенств, связывающих эти переменные?
-
Математический анализ;
-
Линейная алгебра;
-
Аналитическая геометрия;
-
Линейное программирование;
-
Нелинейное программирование.
6. Какой формы записи задач линейного программирования не существует?
-
Общая;
-
Основная;
-
Разветвлённая;
-
Стандартная;
-
нет правильного.
7. В какой форме записана следующая задача линейного программирования
F=c1x1+c2x2+…+cnxn
при условиях:
a11x1+a12x2+…+a1nxn = a10
a21x1+a22x2+…+a2nxn = a20
………………………
am1x1+am2x2+…amnxn = am0
x1,x2,…,xn ≥ 0
-
в общей;
-
в основной;
-
в стандартной;
-
в квадратичной;
-
нет верного.
8. В какой форме записана следующая задача линейного программирования
F=c1x1+c2x2+…+cnxn
при условиях:
a11x1+a12x2+…+a1nxn ≤ a10
a21x1+a22x2+…+a2nxn ≤ a20
………………………
am1x1+am2x2+…amnxn ≥ am0
x1,x2,… ≥ 0
-
в общей;
-
в основной;
-
в стандартной;
-
в квадратичной;
-
нет верного.
9. В какой форме записана следующая задача линейного программирования
F=c1x1+c2x2+…+cnxn
при условиях:
a11x1+a12x2+…+a1nxn ≤ a10
a21x1+a22x2+…+a2nxn ≤ a20
………………………
am1x1+am2x2+…amnxn ≤ am0
x1,x2,…,xn ≥ 0
-
в общей;
-
в основной;
-
в стандартной;
-
в квадратичной;
-
нет верного.
10. В какой задаче линейного программирования ограничения представлены в виде, как равенств, так и неравенств?
-
в основной;
-
в стандартной;
-
в квадратичной;
-
в общей;
-
во всех.
11. В какой задаче линейного программирования все переменные неотрицательны и ограничения имеют форму равенств?
-
в основной;
-
в стандартной;
-
в квадратичной;
-
в общей;
-
во всех.
12. В какой задаче линейного программирования все переменные неотрицательны и ограничения имеют форму однотипных неравенств?
-
в стандартной;
-
в общей;
-
в квадратичной;
-
в основной;
-
во всех.
13. Дайте определение плана.
-
Совокупность чисел X=(x1,x2,…,xn) удовлетворяющих ограничениям задачи ЛП;
-
Совокупность чисел c1, c2, …, cn;
-
Совокупность чисел a10, a20, …, am0;
-
Совокупность чисел X=(x1,x2,…,xn) неудовлетворяющих ограничениям задачи ЛП;
-
Нет верного.
14. Что даёт совокупность чисел X=(x1,x2,…,xn) удовлетворяющих ограничениям задачи ЛП?
-
вектор;
-
нулевой вектор;
-
прямую;
-
план задачи;
-
нет правильного.
15. План X*=(x1*,x2*,…,xn*) при котором целевая функция задачи ЛП принимает своё максимальное (минимальное), значение называется …?
-
Неоптимальным планом;
-
Нулевым решением;
-
Бесконечным решением;
-
Комплексным решением;
-
Оптимальным планом.
16. Дайте определение оптимального плана.
-
план X*=(x1*,x2*,…,xn*) при котором целевая функция задачи ЛП принимает нулевое значение;
-
план X*=(x1*,x2*,…,xn*) при котором целевая функция задачи ЛП принимает своё максимальное (минимальное), значение;
-
совокупность чисел c1, c2, …, cn, при которых целевая функция стремится к бесконечности;
-
совокупность чисел c1, c2, …, cn, при которых целевая функция принимает нулевое значение;
-
нет правильного.
17. Найдите неверный пункт алгоритма перехода от одной формы записи задачи линейного программирования к другой.
-
сводить задачу минимизации функции к задачи максимизации функции;
-
переходить от ограничений в виде неравенств к ограничениям в виде равенств и наоборот;
-
заменять переменные, которые не подчинены условиям не отрицательности;
-
заменять нулями свободные члены;
-
все верны.
18. Что образует непустое множество планов задачи Линейного программирования?
-
Бесконечное пространство;
-
Окружность диаметра d;
-
Многогранник решений;
-
Шар радиуса R;
-
Нет правильного.
19. Каким множеством является планов основной задачи Линейного программирования?
-
выпуклым;
-
невыпуклым;
-
пустым;
-
бесконечным;
-
верны B) и D).
20. Как называется всякая угловая точка многогранника решений?
-
центром;
-
вершиной;
-
серединой боковой стороны;
-
центром тяжести;
-
нет правильного.
21. Как определяется вектор c?
-
По коэффициентам при x целевой функции;
-
По коэффициентам при x первого ограничения системы;
-
По коэффициентам при x второго ограничения системы;
-
Из свободных членов;
-
Произвольно.
22. Из нижеперичисленного выберите уравнение линии уровня.
-
c1x1 - c2x2 = h;
-
a10x1 + a20x2 = h;
-
a10x1 - a20x2 = h;
-
c1x1 + c2x2 = h;
-
(c1x1)/(c2x2) = h;
23. Как называется уравнение c1x1 + c2x2 = h, по которому находится решение задачи ЛП графическим способом?
-
уравнение касательной;
-
уравнение линии уровня;
-
уравнение стороны многогранника решений;
-
уравнение прямой, проходящей через центр многогранника решений;
-
нет правильного.
24. Как направляют линию уровня, чтобы найти решение задачи ЛП на максимум?
-
вдоль оси Ox;
-
вдоль оси Oy;
-
по направлению вектора c;
-
параллельно вектору c;
-
в произвольном направлении.
25. Какой оптимальный план имеет следующая задача
0
x1
x2
1
1
-
(1; 2);
-
(2; 1);
-
(4; 1);
-
(1; 4);
-
задача неразрешима.
26. Какой из нижеперичисленных методов ЛП ещё называют методом последовательного улучшения плана?
-
Симплексный метод;
-
Графический метод;
-
Метод искусственного базиса;
-
Логарифмический метод;
-
Все вышеперечисленные методы.
27. Какой из нижеперичисленных методов ЛП основан на переходе от одного опорного плана к другому при котором значение целевой функции возрастает (если задача задана на максимум)?
-
Графический метод;
-
Абстрактный метод;
-
Симплексный метод;
-
Матричный метод;
-
Верны А) и D).
28. Какое условие необходимо, чтобы использовать симплексный метод для решения задачи ЛП?
-
задача имеет нулевой план;
-
данная задача имеет оптимальный план;
-
данная задача может не иметь оптимального плана;
-
верны А) и В);
-
верны В) и С).
29. Что происходит со значением целевой функции при переходе от одного опорного плана к другому при решении задачи ЛП симплексным методом (задача задана на максимум)?
-
стремится к нулю;
-
убывает;
-
возрастает;
-
верны А) и В);
-
верны А) и С).
30. Что происходит со значением целевой функции при переходе от одного опорного плана к другому при решении задачи ЛП симплексным методом (задача задана на минимум)?
-
убывает;
-
возрастает;
-
стремится к нулю;
-
верны А) и С);
-
верны В) и С).
31. Из скольки этапов складывается решение задача ЛП симплексным методом?
-
5 этапов;
-
4 этапов;
-
3 этапов;
-
2 этапов;
-
1 этапов.
32. На каком этапе находят начальный опорный план задачи ЛП симплексным методом (если в столбце свободных членов есть отрицательные элементы)?
-
на 5 этапе;
-
на 4 этапе;
-
на 3 этапе;
-
на завершающем этапе;
-
на 1 этапе.
33. Какой опорный план находят на начальном этапе при решении задачи ЛП симплексным методом (если в столбце свободных членов есть отрицательные элементы)?
-
начальный опорный план;
-
оптимальный опорный план;
-
нулевой опорный план;
-
промежуточные опорные планы;
-
верны В) и D).
34. Выберите неверный пункт алгоритма нахождения оптимального опорного плана задачи ЛП симплексным методом.
-
разрешающий элемент заменяется обратной величиной;
-
функция меняет знак на противоположный;
-
элементы разрешающей строки делятся на разрешающий элемент;
-
элементы разрешающегося столбца делятся на разрешающий элемент и меняют знак на противоположный;
-
остальные элементы преобразуются по правилу прямоугольника.
35. Какое условие необходимо, чтобы непосредственно записать начальный опорный план симплексным методом?
-
ai0 = 0;
-
ai0 ≥ 0;
-
ai0 ≤ 0;
-
ci > 0;
-
выполнялось A) и D);
36. Что происходит с разрешающим элементом после того как он был найден путём жордановых исключений при решении задачи ЛП симплекс-методом?
-
умножается на 2;
-
заменяется на нулевую величину;
-
заменяется на обратную величину;
-
умножается на -1;
-
делится на -2.
37. Что с разрешающей строкой после того как был найден разрешающий элемент при решении задачи ЛП симплекс-методом?
-
умножается на разрешающий элемент;
-
вычёркивается их симплекс-таблицы;
-
умножается на -1;
-
делится на разрешающий элемент;
-
делится на разрешающий элемент и заменяется на обратную величину.
38. Что с разрешающим столбцом после того как был найден разрешающий элемент при решении задачи ЛП симплекс-методом?
-
делится на разрешающий элемент и заменяет знак на противоположный;
-
умножается на разрешающий элемент;
-
умножается на разрешающий элемент и заменяет знак на противоположный;
-
делится на разрешающий элемент;
-
вычёркивается.
39. Как находят элементы не принадлежащие разрешающей строке и разрешающему столбцу при осуществлении симплексных преобразований над таблицей?
-
заменяют на обратные величины;
-
делят на разрешающий элемент;
-
умножают на разрешающий элемент;
-
по правилу прямоугольника;
-
умножаются на 2.
40. Как определяется разрешающий столбец симплексной таблицы, если в F-строке есть отрицательные элементы?
-
по наибольшему из положительных элементов;
-
по наименьшему из положительных элементов;
-
по нулевому элементу;
-
по наименьшему по абсолютной величине отрицательному элементу;
-
по наибольшему по абсолютной величине отрицательному элементу.
41. Как определяется разрешающая строка после того как в симплексной таблице был найден разрешающий столбец;
-
по наибольшему из элементов разрешающего столбца;
-
по наименьшему из отношений свободных членов к соответствующим положительным элементам разрешающего столбца;
-
по наибольшему из отношений свободных членов к соответствующим положительным элементам разрешающего столбца;
-
по наименьшему из элементов разрешающего столбца;
-
по нулевым элементам разрешающего столбца.
42. Как определяется разрешающий элемент симплекс-таблицы, после того как были найдены разрешающие столбец и строка?
-
на пересечении разрешающей строки и разрешающего столбца;
-
по наибольшему из положительных элементов разрешающей строки;
-
по наименьшему из положительных элементов разрешающей строки;
-
по наибольшему из положительных элементов разрешающего столбца;
-
по наименьшему из положительных элементов разрешающего столбца.
43. При каком условии задача ЛП решаемая симплекс-методом решений не имеет?
-
если в F-строке отрицательные элементы;
-
если все свободные члены положительны;
-
если встретится нулевая строка, все элементы которой равны нулю, а свободный член отличен от нуля;
-
верна A) и B);
-
нет верного.
44. Какой оптимальный план имеет следующая задача?
-
бп
сп
1
-x5
-x4
x3=
3
4
4
x1=
12
-1
1
x2=
2
2
-2
F=
54
1
5
-
(3; 12; 2; 0; 0);
-
(1; 5; 0; 0; 0);
-
(12; 2; 3; 0; 0);
-
(0; 0; 0; 1; 5);
-
(0; 0; 3; 2; 12).
45. При каком условии план задачи ЛП, решаемой симплекс-методом, является оптимальным?
-
все элементы в столбце свободных членов отрицательны;
-
все элементы F-строки отрицательны;
-
в F-строке все элементы нули;
-
в F-строке и столбце свободных членов нет отрицательных элементов;
-
в столбце свободных членов одни нули.
46. Если в F-строке симплексной таблицы есть хотя бы один отрицательный элемент, а в соответствующем ему столбце нет положительных элементов, то …?
-
задача имеет оптимальный план;
-
задача неразрешима;
-
опорный план не оптимален, и можно перейти к новому опорному плану;
-
задача имеет только нулевое решение;
-
нет правильного.
47. Если в F-строке симплексной таблицы есть хотя бы один отрицательный элемент, а в соответствующем ему столбце есть положительные элементы, то …?
-
задача имеет оптимальный план;
-
задача неразрешима;
-
опорный план не оптимален, и можно перейти к новому опорному плану;
-
задача имеет только нулевое решение;
-
в столбце свободных членов одни нули.
48. Если в столбце свободных членов и F-строке симплексной таблицы нет отрицательных элементов, то …?
-
задача имеет оптимальный план;
-
задача неразрешима;
-
опорный план не оптимален, и можно перейти к новому опорному плану;
-
задача имеет только нулевое решение;
-
нет правильного.
49. Если в столбце свободных членов есть отрицательный элемент и в соответствующей строке есть хотя бы один отрицательный элемент, то …?
-
план является оптимальным;
-
найден начальный опорный план;
-
задача неразрешима;
-
план не является опорным и его можно найти;
-
нет правильного.
50. Если в столбце свободных членов есть отрицательный элемент, и в соответствующей строке нет отрицательных элементов, то …?
-
план является оптимальным;
-
найден начальный опорный план;
-
задача неразрешима;
-
план не является опорным и его можно найти;
-
нет правильного.
51. До каких пор применяют симплекс-метод к решению задач ЛП, если задача имеет решение?
-
пока не будет найден начальный опорный план;
-
пока не будет найден оптимальный план или установлена неразрешимость задачи;
-
пока не будет найден разрешающий элемент;
-
пока не будет найдена разрешающая строка;
-
пока не будет найден разрешающий столбец.
52. По какой формуле можно свести задачу минимизации функции к задаче максимизации функции?
-
min(F)=max(F);
-
min(F)=max(F/10);
-
min(F)=-max(F);
-
min(F)=max(-F);
-
min(F)=-max(-F).
53. Выберите признак оптимальности опорного плана задачи минимизации функции, решаемой симплекс-методом.
-
отсутствие положительных элементов в F-строке симплекс-таблицы;
-
отсутствие отрицательных элементов в F-строке симплекс-таблицы;
-
отсутствие нулевых элементов в F-строке симплекс-таблицы;
-
отсутствие дробных элементов в F-строке симплекс-таблицы;
-
нет правильного.
54. Какой оптимальный план имеет следующая задача (max)?
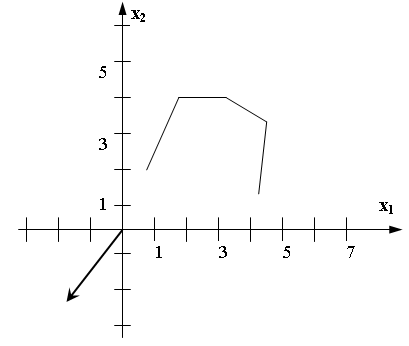
-
(2; 4);
-
(3; 4);
-
Задача неразрешима;
-
(1; 1);
-
(3; 3).
55. Какой оптимальный план имеет следующая задача (max)?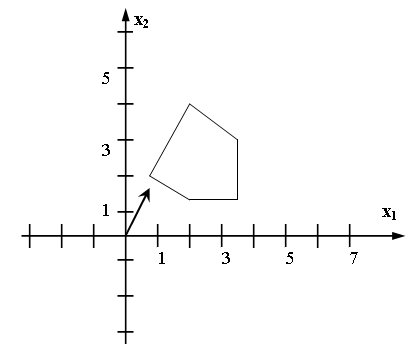
-
(2; 4);
-
(0; 3);
-
(1; 1);
-
(3; 1);
-
(4; 2).
56. Какой оптимальный план имеет следующая задача (max)?
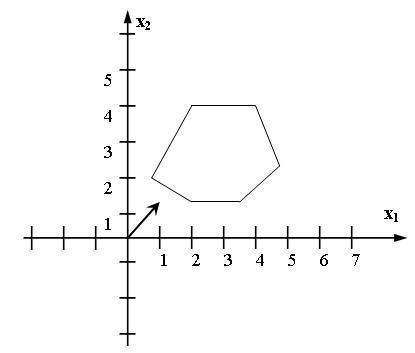
-
(2; 4);
-
(1; 1);
-
(5; 3);
-
(4; 4);
-
(0; 4).
57. Какой оптимальный план имеет следующая задача (min)?
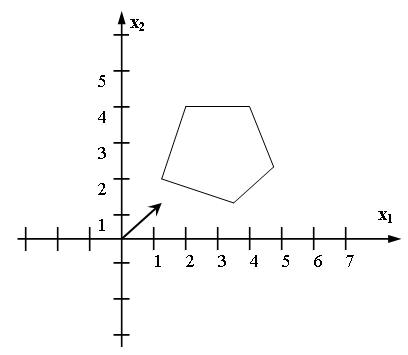
-
(2; 4);
-
(1; 2);
-
(2; 5);
-
(5; 2);
-
(4; 4).
58. Какой оптимальный план имеет следующая задача (min)?
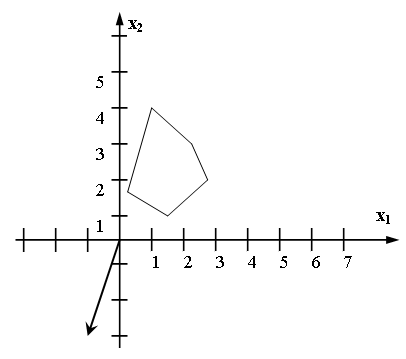
-
(2; 5);
-
(1; 2);
-
(1; 1);
-
(3; 1);
-
(1; 4).
59. Какие координаты будет иметь вектор с, если задана следующая задача?
F = x1 + x2 → max
при условиях
2x1 + 4x2 ≤ 16;
2x1 - 4x2 ≤ 8;
x1 + 3x2 ≥ 9;
x1, x2 ≥ 0
-
(0; 0);
-
(1; 3);
-
(1; 1);
-
(2; -4);
-
(2; 4).
60. Какие координаты будет иметь вектор с, если задана следующая задача?
F = -6x1 + 2x2 → max
при условиях
x1 + 2x2 ≤ 9;
-1x1 - 4x2 ≤ -2;
-2x1 + 5x2 ≥ 3;
x1, x2 ≥ 0
-
(-6; 2);
-
(1; 2);
-
(-1; -4);
-
(-2; 5);
-
(0; 0).
61. Какой оптимальный план имеет следующая задача (max)?
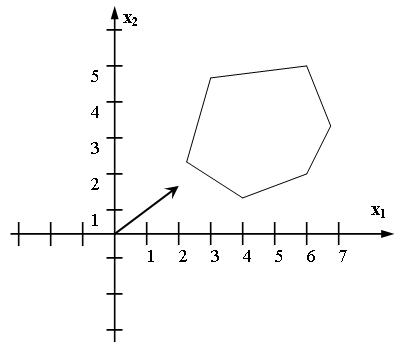
-
(3; 2);
-
(3; 5);
-
(6; 5);
-
(7; 1);
-
(1; 1).
62. Сколько базисных переменных будет добавлено к следующей задаче ЛП, записанной в стандартной форме, если данная задача решается симплекс-методом?
F = -2x1 + x2+ 6 (max);
3x1 + x2 ≥ 6;
4x1 + 5x2 ≥ 19;
4x1 + 3x2 ≥ 24;
xj ≥ 0.
-
1;
-
2;
-
4;
-
5;
-
3.
63. Сколько базисных переменных будет добавлено к следующей задаче ЛП, записанной в стандартной форме, если данная задача решается симплекс-методом?
F = 5x1 + 4x2+ 6 (min);
-x1 + 2x2 ≤ -12;
2x1 - 2x2 ≥ 2;
-7x1 + 4x2 ≤ 5;
2x1 - 3x2 ≥ 1;
xj ≥ 0.
-
1;
-
4;
-
3;
-
5;
-
2.
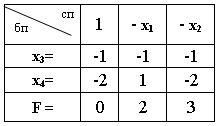
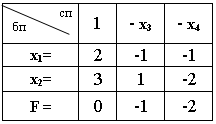
64. Составьте начальную симплекс-таблицу для следующей задачи ЛП.
F = 2x1 + 3x2 (max);
x1 + x2 ≥ 1;
-x1 + 2x2 ≥ 2;
xj ≥ 0.
-
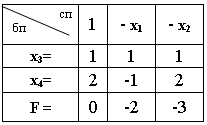
-
-
-
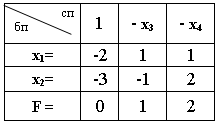
-
нет правильного
65. Какой начальный опорный план имеет следующая задача ЛП?
F = 5x1 + 4x2+ 6 (max);
2x1 + 5x2 ≥ 3;
2x1 - 2x2 ≥ 5;
-21 + x2 ≥ 6;
xj ≥ 0
-
(5; 4; 0; 0; 0);
-
(0; 0; 0; 5; 4);
-
(0; 0; 0; 0; 6);
-
(0; 0; 3; 5; 6);
-
(3; 5; 6; 0; 0).
| 1 | -x1 | -x2 | |
| x3= | -2 | 1 | 1 |
| x4= | -3 | -1 | 2 |
| x5= | 5 | 1 | 5 |
| F = | 0 | -1 | 2 |
-
(0; 0; -2; -3; 5);
-
задача не имеет начального опорного плана;
-
(-2; -3; 0; 0; 0);
-
(0; 0; -2; -3; 5);
-
(1; 2; 0; 0; 0).
| 1 | -x1 | -x2 | |
| x3= | 5 | 1 | 4 |
| x4= | 2 | -1 | -1 |
| x5= | 1 | 1 | 3 |
| F = | 0 | -3 | -1 |
-
(0; 0; 0; -3; -1);
-
(-3; -1; 0; 0; 0);
-
(0; 0; 5; 2; 1);
-
(5; 2; 1; 0; 0);
-
задача не имеет начального опорного плана.
| 1 | -x1 | -x2 | -x3 | |
| x4= | -5 | 1 | -4 | 2 |
| x5= | 3 | 1 | 1 | -2 |
| x6= | 5 | 5 | 3 | 2 |
| x7= | 1 | 3 | -3 | 6 |
| F = | 0 | -3 | -1 | 9 |
-
в строке x4;
-
в строке x5;
-
в строке x6;
-
в строке x7;
-
задача неразрешима.
| 1 | -x1 | -x2 | -x3 | |
| x4= | 6 | 3 | -4 | 6 |
| x5= | 5 | 1 | -3 | -2 |
| x6= | 1 | -5 | 1 | 2 |
| F = | 0 | -3 | -1 | 2 |
-
на пересечении строки x5 и столбца x3;
-
на пересечении строки x4 и столбца x2;
-
на пересечении строки x6 и столбца x1;
-
на пересечении строки x4 и столбца x1;
-
на пересечении строки x5 и столбца x1.
| 1 | -x1 | -x2 | |
| x3= | 4 | 2 | -9 |
| x4= | 8 | 1 | -3 |
| F = | 0 | -6 | 5 |
-
-9;
-
-3;
-
1;
-
0;
-
2.
| 1 | -x2 | -x5 | |
| x1= | 1 | -1 | 2 |
| x4= | 3 | 1 | 4 |
| x3= | 5 | 3 | -1 |
| F = | 18 | 2 | 1 |
-
(1; 3; 5; 0; 0);
-
(1; 0; 5; 3; 0);
-
(0; 0; 1; 3; 5);
-
(2; 1; 0; 0; 0);
-
(0; 0; 0; 2; 1).
| 1 | -x3 | -x5 | |
| x2= | 4 | 1 | 0 |
| x4= | 3 | 0 | 2 |
| x1= | 2 | -1 | 3 |
| F = | 1 | -3 | -1 |
-
(0; 0; 0; -3; -1);
-
(-3; -1; 0; 0; 0);
-
(2; 4; 0; 3; 0);
-
(4; 3; 2; 0; 0);
-
(0; 0; 4; 3; 2).
73. Дана задача ЛП, решаемая симплекс-методом
F = 2x1 + 3x2 – x3 (max)
x1 – x2 + 2x3 ≥ 6;
2x1 + x2 – x3 ≥ 2.
xi ≥ 0.
Запишите F-строку начальной симплекс-таблицы.
-
F =
0
-2
-3
1
-
F =
0
2
3
-1
-
F =
0
1
-1
2
-
F =
0
2
1
-1
| 0 | 6 | 2 |
74. Дана целевая функция задачи ЛП F = x1 + 3x2 – x3 (max). Оптимальный план равен 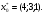 Вычислить значение целевой функции.
Вычислить значение целевой функции.
-
20;
-
16;
-
8;
-
10;
-
12.
75. Дана целевая функция задачи ЛП F = 3x1 - x2 – x3 (min). Оптимальный план равен 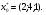 Вычислить значение целевой функции.
Вычислить значение целевой функции.
-
4;
-
6;
-
-3;
-
1;
-
0.
| 1 | -x2 | -x3 | |
| x1= | 4 | 1 | 0 |
| x4= | 6 | 2 | 3 |
| F = | 5 | -2 | 1 |
-
(0; 0; 1; 3);
-
(1; 3; 0; 0);
-
(0; 0; 4; 6);
-
(0; 2; 1; 0);
-
(0; 3; 0; 4).
| 1 | -x4 | -x1 | |
| x2= | 4 | 0 | -1 |
| x3= | 2 | 1 | 1 |
| F = | 1 | 4 | -3 |
-
(2; 6; 0; 0);
-
(0; 6; 3; 1);
-
(0; 0; 6; 2);
-
(0; 7; 3; 0);
-
(0; 3; 1; 0).
| 1 | -x4 | - x5 | |
| x2= | 4 | 2 | 3 |
| x1= | 3 | 0 | 1 |
| x3= | 1 | 1 | 0 |
| F = | ? | 4 | -3 |
-
9;
-
10;
-
13;
-
16;
-
8.
79. Какой оптимальный план имеет следующая задача (max)?
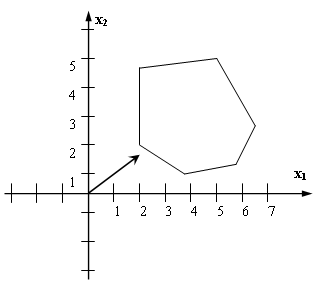
-
(3; 5);
-
(7; 5);
-
(1; 4);
-
(5; 5);
-
(4; 1).
80. Какой оптимальный план имеет следующая задача (min)?
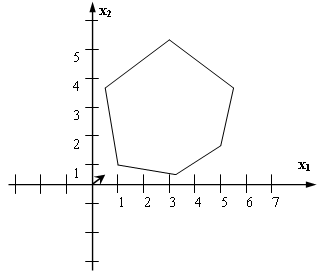
-
(1; 1);
-
(4; 4);
-
(5; 5);
-
(3; 6);
-
(2; 4).
81. С чего начинается решение задачи ЛП симплекс-методом?
-
с изменения знаков свободных членов на противоположные;
-
с построения многоугольника решений;
-
с нахождения какого-либо опорного плана;
-
с нахождения оптимального плана;
-
нет правильного.
82. Когда завершают процесс решения задачи ЛП симплекс-методом?
-
когда найден какой-либо опорный план;
-
когда найден оптимальный план;
-
когда матрица, составленная из коэффициентов при неизвестных примет треугольный вид, где все элементы ниже главной диагонали равны нулю;
-
когда матрица, составленная из коэффициентов при неизвестных примет треугольный вид, где все элементы выше главной диагонали равны нулю;
-
когда функция станет равной нулю.
83. Какой метод используется при решении задачи ЛП, когда к системе ограничительных уравнений нельзя непосредственно добавить единичные векторы?
-
графический метод;
-
симплекс-метод;
-
метод северо-западного угла;
-
метод искусственного базиса;
-
метод Фогеля.
84. Когда при решении задач ЛП используется метод искусственного базиса?
-
когда нельзя непосредственно добавить к системе ограничительных уравнений единичные векторы;
-
когда все
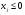 ;
; -
когда все
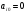 ;
; -
верны В) и С);
-
нет верного.
85. Как называются переменные, которые добавляются к системе ограничительных уравнений в методе искусственного базиса?
-
нулевыми;
-
комплексными;
-
вторичными;
-
функциональными;
-
искусственными.
86. Что происходит с линейной функцией (max) в методе искусственного базиса, после того как к системе ограничительных уравнений были добавлены искусственные переменные?
-
она меняет знак;
-
сумма этих переменных, умноженная на как угодно большое положительное число, вычитается из линейной функции;
-
если функция на максиму, то она минимизируется;
-
если функция на минимум, то она максимизируется;
-
нет правильного.
87. Какой вид принимает целевая функция (max) при решении задачи ЛП методом искусственного базиса?
-
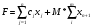 ;
; -
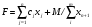 ;
; -
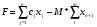 ;
; -
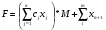 ;
; -
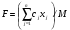 .
.
88. Что происходит с линейной функцией (min) в методе искусственного базиса, после того как к системе ограничительных уравнений были добавлены искусственные переменные?
-
сумма этих переменных, умноженная на как угодно большое положительное число, прибавляется к линейной функции;
-
она меняет знак;
-
если функция на максиму, то она минимизируется;
-
если функция на минимум, то она максимизируется;
-
нет правильного.
89. Какой вид принимает целевая функция (min) при решении задачи ЛП методом искусственного базиса?
-
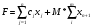 ;
; -
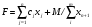 ;
; -
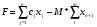 ;
; -
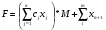 ;
; -
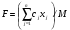 .
.
90. Какой базис образуют переменные 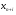 , добавляемые к системе ограничительных уравнений при решении задачи ЛП методом искусственного?
, добавляемые к системе ограничительных уравнений при решении задачи ЛП методом искусственного?
-
нулевой;
-
функциональный;
-
искусственный;
-
базис Гомори;
-
нет правильного.
91. Если в оптимальном плане М-задачи по методу искусственного базиса все искусственные переменные 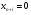 (i = 1,2, …, n), то … .
(i = 1,2, …, n), то … .
-
план
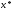 является оптимальным планом исходной задачи;
является оптимальным планом исходной задачи; -
план x является начальным опорным планом исходной задачи;
-
исходная задача имеет только нулевое решение;
-
задача неразрешима;
-
нет правильного.
92. При каком условии план x является оптимальным по методу искусственного базиса?
-
все искусственные переменные
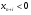 ;
; -
все искусственные переменные
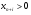 ;
; -
все искусственные переменные
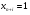 ;
; -
все искусственные переменные
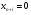 ;
; -
при любом условии.
93. Если в оптимальном плане М-задачи по методу искусственного базиса по крайней мере одна из искусственных переменных положительна при любом большом М, то … .
-
задача имеет только нулевое решение;
-
задача имеет бесконечное множество решений;
-
исходная задача не имеет ни одного плана;
-
опорный план является оптимальным;
-
нет правильного.
94. Выберите условие, при котором задача ЛП, решаемая методом искусственного базиса не имеет ни одного плана.
-
все искусственные переменные отрицательны;
-
когда, по крайней мере, одна из искусственных переменных положительна;
-
если все искусственные переменные равны нулю;
-
когда все коэффициенты при неизвестных x1 отрицательны;
-
нет правильного.
95. Если М-задача по методу искусственного базиса не имеет решения, то … .
-
исходная задача имеет оптимальный план;
-
исходная задача имеет бесконечное множество решений;
-
исходная задача имеет только нулевое решение;
-
исходная задача неразрешима;
-
нет правильного.
96. Сколько слагаемых будет содержать целевая функция задачи ЛП, если она решается по методу искусственного базиса?
-
2;
-
3;
-
4;
-
5;
-
6.
97. До каких пор осуществляют процесс жордановых преобразований по методу искусственного базиса?
-
когда все искусственные переменные станут отрицательными;
-
пока из базиса не будут исключены все искусственные переменные;
-
пока в F-строке значение целевой функции станет равным нулю;
-
пока в первой строке таблицы окажутся все нули;
-
нет правильного.
98. Сколько искусственных переменных будет добавлено к следующей задаче ЛП, записанной в стандартной форме, если данная задача решается методом искусственного базиса?
F = 2x1 - 3x2 (max);
x1 + 5x2 = 5;
-2x1 + 2x2 = -2;
x1 - 3x2 = 3;
xj ≥ 0.
-
1;
-
2;
-
3;
-
4;
-
5.
99. Сколько искусственных переменных будет добавлено к следующей задаче ЛП, записанной в стандартной форме, если данная задача решается методом искусственного базиса?
F = 2x1 - 3x2 + x3 (max);
x1 + 2x2 - 2x3 = 1;
5x1 + x2 +3x3 = 5;
x1 - 4x2 +4x3 = 2;*
xj ≥ 0.
-
2;
-
1;
-
3;
-
4;
-
5.
100. Сколько ограничительных уравнений содержит система ограничений задачи ЛП, если решая её по методу искусственного базиса к ней было добавлено 2 искусственные переменные?
-
5;
-
4;
-
3;
-
1;
-
2.
Здесь представлены материалы теста на тему «Тест по информатике для 7 класса», которые могут быть просмотрены в онлайн режиме или же их можно бесплатно скачать. Предмет теста: Информатика (7 класс). Также здесь Вы найдете подборку тестов на схожие темы, что поможет в еще лучшей подготовке к тестированию.

