Презентация "Доверительный интервал и доверительная вероятность" по обществознанию – проект, доклад

Выполнила: студентка Адутова А.Р. Группы 3ТБб-02-21оп Проверил: преподаватель Шестаков Н.И.

Доверительный интервал и доверительная вероятность.

В результате отдельных измерений мы получаем некоторые строго фиксированные результаты (точки) измеряемой величины. Их значения являются случайными с некоторым распределением.

На практике мы всегда имеем дело с ограниченным числом измерений, и задача, которая всегда стоит перед оператором, состоит в том, как оценить точность измерений, т.е. найти его меру приближения к истинному значению на основании группы результатов наблюдения.

Понятие о доверительных интервалах.

После получения точечной оценки θ* желательно иметь данные о надежности такой оценки. Особенно важно иметь сведения о точности оценок для небольших выборок. Поэтому точечная оценка может быть дополнена интервальной оценкой — интервалом (θ1, θ 2), внутри которого с наперед заданной вероятностью γ находится точное значение оцениваемого параметра θ.

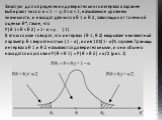
Зачастую для определения доверительного интервала заранее выбирают число α = 1 — γ, 0 θ 2 ) = α/2 (рис. 1)

Длина доверительного интервала, характеризующая точность интервальной оценки, зависит от объема выборки п и надежности γ (уровня значимости γ= 1 - α). При увеличении величины п длина доверительного интервала уменьшается, а с приближением надежности γ к единице — увеличивается. Выбор α (или γ = 1 - α) определяется конкретными условиями. Обычно используется α=0,1; 0,05; 0,01, что соответствует 90, 95, 99%-м доверительным интервалам.

Общая схема построения доверительного интервала: 1. Из генеральной совокупности с известным распределением f(x, θ) случайной величины X извлекается выборка объема п, по которой находится точечная оценка θ * параметра θ. 2. Строится случайная величина Y(θ), связанная с параметром θ и имеющая известную плотность вероятности f(у, θ). 3. Задается уровень значимости α. 4. Используя плотность вероятности случайной величины Y, определяют два числа с1 и с2 такие, что (2) Значения с1 и с2 выбираются как правило, из условий

Интервальная оценка также носит случайный характер, так как она напрямую связана с результатами выборки. Однако она позволяет сделать следующий вывод. Если построен доверительный интервал, который с надежностью γ = 1 - α накрывает неизвестный параметр, и его границы рассчитываются по К выборкам одинакового объема п, то в (1-α)К случаях построенные интервалы накроют истинное значение исследуемого параметра.

Пример 2. Найти доверительный интервал для оценки неизвестного математического ожидания нормально распределенного признака, если известны: σ = 2; = 5,4; n = 10; γ = 0,95. Решение. 2Ф(t) = 0,95, Ф(t) = 0,5*0,95=0,475. Найдя t = 1,96, получим Доверительный интервал

Генеральной совокупностью называется множество всех возможных значений или реализаций исследуемой случайной величины при данном реальном комплексе условий. Выборкой называют часть генеральной совокупности, отобранную для изучения. Изучение всей генеральной совокупности во многих случаях либо невозможно, либо нецелесообразно в силу больших материальных затрат, поэтому на практике часто приходится иметь дело с выборками небольшого объема п

Генеральная совокупность.

Построение доверительного интервала для генеральной средней по малой выборке.

Используя свойства математического ожидания и дисперсии, получим, что:

Пример 5. Для контроля срока службы электроламп из большой партии было отобрано 17 электроламп. В результате испытаний оказалось, что средний срок службы отобранных ламп равен 980 ч, а среднее квадратическое отклонение их срока службы — 18 ч. Необходимо определить: а) вероятность того, что средний срок службы ламп во всей партии отличается от среднего срока службы отобранных для испытаний ламп не более чем на 8 ч (по абсолютной величине); б) границы, в которых с вероятностью 0,95 заключен средний срок службы ламп во всей партии. Решение. Имеем по условию п = 20, = 980(ч), S = 18 ч. а) Зная предельную ошибку малой выборки = 8 (ч), найдем из соотношения (9): Теперь искомая доверительная вероятность , а находится по таблице значений при числе степеней свободы = 16. Итак, вероятность того, что расхождение средних сроков службы электроламп в выборке и во всей партии не превысит 8 ч (по абсолютной величине), равна 0,906.

Построение доверительного интервала для генеральной доли по малой выборке. где – фактическое число элементов выборки, обладающих признаком.

Пример 6. Опрос случайно отобранных 15 жителей города показал, что 6 из них будут поддерживать действующего мэра на предстоящих выборах. Найти границы, в которых с надёжностью 0,9 заключена доля граждан города, которые будут поддерживать на предстоящих выборах действующего мэра. Решение. Выборочная доля жителей, поддерживающих мэра, w = т/п = 6/15 = 0,4 . По рисунку 3 для γ = 0,9 находим при w = 0,4 и для п = 15 по нижнему графику p1=0,23, а по верхнему — р2 = 0,60, т.е. доля жителей города, поддерживающих мэра, с надёжностью 0,9 заключена в границах от 0,23 до 0,60. Очевидно, что более точный ответ на вопрос задачи может быть получен при увеличении объёма выборки п.

В данной работе рассмотрено понятие доверительного интервала и его разновидности в метрологии. Провести бесконечное число измерений для получения верного результата в реальной жизни невозможно, поэтому важно дать объективное представление результатов ограниченного числа измерений, чему и призван помочь изучаемый подход. Цель любого оценивания состоит в получении наиболее точного значения исследуемой характеристики. Доверительный интервал позволяет с определенной точностью получить распределение параметра, что дает хорошее представление об исследуемом объекте.

Заключение