Конспект урока «ПРЕОБРАЗОВАНИЕ ПОДОБИЯ» по математике для 9 класса
Разработка урока по геометрии с применением технологии критического мышления.
Вводное учебное занятие с использованием технологии развития критического мышления.
Учитель: Крючкова И.А.
УРОК ПО ТЕМЕ: «ПРЕОБРАЗОВАНИЕ ПОДОБИЯ» (9класс).
Цели:
-
Актуализировать личностные опорные знания учащихся к изучению новой темы ;
-
Создать содержательные и организационные условия для развития у школьников критического мышления;
-
Обеспечить создание у школьников образного представления о преобразованиях плоскости;
-
Создать условия развития у школьников аналитических и синтетических навыков
(сотрудничество, умение высказывать свою точку зрения).
Оборудование: тетради, чертёжные инструменты, таблицы с изображением различных видов движений, подобия и гомотетии, тексты с новым материалом.
| ДЕЯТЕЛЬНОСТЬ УЧИТЕЛЯ | ДЕЯТЕЛЬНОСТЬ УЧАЩИХСЯ | ФОРМА РАБОТЫ | |
| 1.Вызов ( актуализация субъективного опыта). | Создание условий для активизации знаний, формирование проблемы и цели на основе мотивации. 1.Вспомните и напишите у себя в тетрадях всё, что вы знаете о преобразованиях плоскости. 2. В тетради нарисуйте маркировочную таблицу с тремя одинаковыми колонками. 3. В левой колонке таблицы запишите всё, что вы знаете о преобразованиях плоскости. 4. Обменяйтесь своими знаниями в паре. 5. Давайте обсудим то. что у нас получилось. Записывает на доске в левой колонке таблицы всё, что говорят учащиеся. Первая колонка таблицы маркируется словом «Знаю». | 1.Каждый в тетради записывает всё, что помнит о преобразованиях плоскости. 2.Рисуют маркировочную таблицу. 3.Записывают в левую колонку всё, что вспомнили о познавательном объекте. 4.Обмениваются друг с другом своими знаниями. 5.Каждый по очереди информирует класс о том, что знает о рассматриваемом объекте. Левая колонка таблицы маркируется словом «Знаю». Дополняют записи в левой колонке таблицы. | Индивидуально. В парах. Фронтально. |
| 2.Осмысление. Создание условий для обобщения изученного ранее материала, обозначение проблемных вопросов. | 1.Попробуйте классифицировать записанные на доске знания. 2. На доске оформляется структурно- логическая схема ( см. после таблицы). Учитель обращает внимание учащихся на приготовленные ранее таблицы. | 1.Предлагают основания для классификации полученных о преобразованиях плоскости сведениях. 2.Записывают структурно-логическую схему, обсуждая вопрос о распределении по предложенным основаниям полученных на предыдущем этапе сведений. | Фронтально. |
| 3.Чтение с пометками. Получение новой информации. | 1. Предлагает каждому ученику текст ( см. ниже). 2.Ччитайте и делайте в тексте пометки (не более 10 мин.) Пометки: «V» - «знаю»; «-» - « противоречит моим первоначальным представлениям»; «?» - «хочу знать»; «+» - « это для меня новое». 3. Продолжите работу с маркировочной таблицей индивидуально. 4. Маркирует две оставшиеся колонки таблицы: «Хочу узнать» и «Узнал новое». 5. Давайте обсудим данные, записанные в третьей колонке в ходе самостоятельной работы. Заполняет вместе с учащимися колонку таблицы «Узнал новое». 6.Давайте обсудим данные, записанные вами во второй колонке таблицы «Хочу узнать». Заполняет в ходе обсуждения вторую колонку таблицы. 7.Является ли преобразование подобия движением? Почему? Какие свойства подобия сходны со свойствами движения? Какие утверждения из прочитанного вами текста требуют доказательства? Кто может к следующему занятию разобрать по учебнику и представить доказательства , изложенных фактов? 8. Установка на домашнее задание: «К следующему уроку необходимо ответить на возникшие вопросы. Если возникнут затруднения, попробуем разобрать вместе.» | Получают распечатку текста, содержащего информацию о новом представителе преобразования плоскости «Подобии». 2. Читают текст и на полях делают пометки. 3. Самостоятельно в тетрадях заполняют маркировочную таблицу в соответствии со сделанными пометками. 4.Учавствуют в обсуждении 5. Отвечают на вопросы учителя. | Индивидуально. Фронтально. |
| 3.Рефлексия. Создание условий для обобщения полученной информации | Используется методика неоконченного предложения: « Сегодня на уроке мы узнали…»; «Преобразование подобия - это…»; «Преобразование подобия является движением при …»; «Преобразование подобия обладает следующими свойствами…»; «Гомотетией называется…»; «Фигура F называется подобной фигуре F2 , если…» | Фронтально. | |
| 5.Домашнее задание. | Доработайте сформированную в ходе занятия структурно-логическую схему с учётом новой информации. Подготовьте доказательства следующих утверждений: гомотетия есть преобразование подобия ; Преобразование подобия сохраняет углы между полупрямыми; Если фигура F1 подобна фигуре F2, а фигура F2 подобна фигуре F3, то фигуры F1 и F3 подобны. (Использовать учебник стр. 145 – 148). | Записывают задание на дом. | Индивидуально. |
Структурно-логическая схема
Преобразования плоскости
Движения
Не являющиеся движением дввввдвижениями
свойства
виды
Поворот
Параллельный перенос
Симметрия относительно точки и относительно прямой.
Способы построения
Текст «Преобразование подобия»
Преобразование фигуры F в фигуру F´ называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и тоже число раз.

Это значит, что если произвольные точки X и Y фигуры F при преобразовании подобия переходят в точки X´ и Y´ фигуры F´, то X´ Y´ = k XY, причём число k одно и тоже для всех точек X и Y . Число k называется коэффициентом подобия. При k = 1 преобразование подобия является движением.
Две фигуры называются подобными, если они переводятся друг в друга преобразованием подобия. Для обозначения подобия фигур используется специальный значок: ~. Запись F~ F´ читается так: «Фигура F подобна фигуре F´».
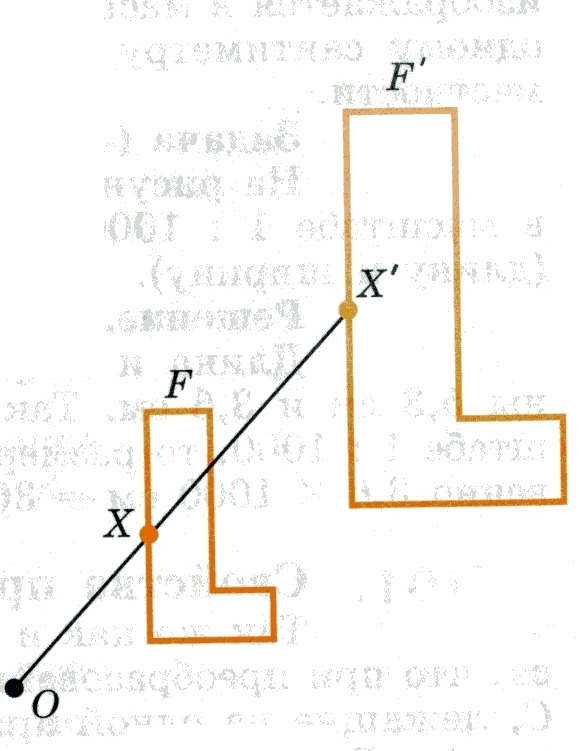
Пусть F – данная фигура и О – фиксированная точка. Проведём через произвольную точку X фигуры F луч ОX и отложим на нём отрезок ОX´, равный k ОX, где k - положительное число. Преобразование фигуры F, при котором каждая её точка X переходит в точку X´, построенную указанным способом, называется гомотетией относительно центра О. Число k называется коэффициентом гомотетии, фигуры F и F´ называются гомотетичными.
Гомотетия есть преобразование подобия.
Свойства подобия:
-
При преобразовании подобия прямые переходят в прямые, отрезки в отрезки, лучи в лучи.
-
Преобразование подобия сохраняет углы между полупрямыми.
-
При преобразовании подобия три точки А, В, С, лежащие на одной прямой, переходят в точки также лежащие на одной прямой. Причём если точка В лежала между точками А и С, то точка В´лежит между точками А´ и С´.
-
Если фигура F1 подобна фигуре F2, а фигура F2 подобна фигуре F3, то фигуры F1 и F3 подобны.
-
У подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, у подобных треугольников АВС и А1В1С1 1, 1, 1;
АВ/ А1В1 = ВС/В1С1 = АС/А1С1.
Преобразование подобия широко применяется на практике при выполнении чертежей деталей машин, сооружений, планов местности, изготовлении макетов и др. Эти изображения представляют собой подобные преобразования воображаемых изображений в натуральную величину. Коэффициент подобия при этом называется масштабом. Например, если участок местности изображается в масштабе 1: 100, то это значит, что одному сантиметру на плёнке соответствует 1м на местности.
Анализ урока.
Данный урок является первым уроком при изучении темы «Преобразование фигур» и первым уроком в 9 классе после повторения материала, изученного в 8 классе.
Урок организован по технологии развитие критического мышления через чтение и письмо. Он представляет собой комплекс заданий, выполняя которые учащиеся 9 класса подойдут к пониманию темы «Преобразование подобия», помогает включению в работу всех без исключения учащихся.
Урок предполагает разнообразные по форме и содержанию задания для учащихся:
1)работа с текстом ;
2)эвристические задания;
3)индивидуальная работа;
4)групповая работа;
5)фронтальная;
6)работа со структурно-логической схемой.
Урок охватывает не всю тему, но создает условия для осознанного изучения материала и получения нового; способствует осмыслению нового материала и систематизации ранее изученного; даёт возможность развитию навыка анализа материала, навыка групповой работы учащихся; развивает исследовательские умения учащихся.
Здесь представлен конспект к уроку на тему «ПРЕОБРАЗОВАНИЕ ПОДОБИЯ», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

