Тест на тему «Математические основы программирования»

1. информация, алгоритм, программа, исполнитель

2. система команд исполнителя, система счисления

3. двоичная арифметика, логические операции

1. 1, 2

2. 1, 3

3. 2, 3

4. 1, 2, 3

5. среди перечисленных нет правильного ответа

2 Первые программы для управления ЭВМ появились в

1. первом поколении

2. втором поколении

3. третьем поколении

4. четвёртом поколении

5. пятом поколении

3 Под термином «поколение ЭВМ» понимается

1. совокупность машин, предназначенных для обработки, хранения и передачи информации

2. все счётные машины

3. все типы и модели ЭВМ, построенные на одних и тех же научных и технических принципах

4. все типы моделей процессоров Pentium

5. год выпуска ЭВМ

4 Разработка основных принципов цифровых вычислительных машин принадлежит

1. Лейбницу

2. Блезу Паскалю

3. Джону фон Нейману

4. Чарльзу Беббиджу

5. Орднеру

5 Первая машина, выполняющая автоматически все арифметические операции

1. абак

2. машина С.А.Лебедева

3. машина Беббиджа

4. машина Чебышева

5. МЭСМ

6 Первоначальный смысл слова «компьютер»:

1. электронный аппарат

2. вид телескопа

3. электронно-лучевая трубка

4. человек, производящий расчёты

5. электронно-вычислительное устройство

7 Основоположником математической логики считается

1. Чарльз Беббидж

2. Готфрид Вильгельм Лейбниц

3. Блез Паскаль

4. Джордж Буль

5. Джон фон Нейман

8 Основоположником двоичной системы счисления является

1. Чарльз Беббидж

2. Готфрид Вильгельм Лейбниц

3. Блез Паскаль

4. Джордж Буль

5. Джон фон Нейман

9 К основным этапам решения задачи на ЭВМ относятся:

1. идентификация, концептуализация, формализация, выполнение, тестирование и опытная эксплуатация

2. постановка, моделирование, разработка алгоритма, программирование, выполнение, анализ результатов

3. анализ, алгоритмизация, программирование, выполнение и тестирование

4. постановка, формализация, выполнение, тестирование

5. математическое моделирование, программирование, выполнение, анализ результатов

10 Этап формализации задачи означает:

1. построение математической модели задачи

2. построение алгоритма решения задачи

3. запись алгоритма на формальном языке

4. тестирование работоспособности программы

5. анализ полученных результатов

11. Измерение параметров окружающей среды (температуры, воздуха, атмосферного давления и пр.) на метеостанции представляет собой информационный процесс …

1. хранения информации

2. получения информации

3. передачи информации

4. защиты информации

5. обработки информации

12 Информационный процесс представляет собой …

1. содержание сообщения

2. поиск, передачу, хранение, обработку информации

3. объем информации

4. все ответы верны

5. нет правильного ответа

13. К основным свойствам алгоритма относятся:

1. дискретность, массовость, определенность, результативность

2. понятность, полнота, простота, сложность

3. непрерывность, непротиворечивость, актуальность, научность

4. линейность, цикличность, выборка

5. линейные, разветвляющиеся, циклические

14. По структуре алгоритмы классифицируются на:

1. линейные, циклические, антициклические

2. простые, сложные

3. переборные, комбинаторные

4. линейные, разветвляющиеся, циклические

5. циклы с параметром, условные циклы

14. К основным базовым конструкциям алгоритма относятся:

1. следование, развилка, цикл

2. циклы с параметром, циклы с условием

3. развилка, выбор, цикл

4. линейные, разветвляющиеся

5. разветвляющиеся, циклические

14. Основными типами циклических конструкций являются:

1. полная, неполная конструкция

2. циклы с предусловием, с постусловием, с параметром

3. линейная, разветвляющаяся, циклическая конструкции

4. циклы с предусловием, с постусловием

5. простые, сложные циклы

14. Происхождение термина «алгоритм» связано с именем ученого …

1. Аль Фараби

2. Аль Хорезми

3. Никлаус Вирт

4. Блез Паскаль

5. Евклид

14. Первый разработанный алгоритм принадлежит …

1. Декарту

2. Евклиду

3. Аль Хорезми

4. Аль Фараби

5. Никлаусу Вирту

14. Принципы программного управления ЭВМ впервые были сформулированы …

1. Евклидом

2. Декартом

3. Паскалем

4. Никлаусом Виртом

5. Фон Нейманом

14. Разработка языка программирования Pascal принадлежит …

1. Б. Паскалю

2. Н. Вирту

3. Чебышеву

4. Дейкстре

5. Л.Эйлеру

14. Основоположником тории графов является …

1. Леонард Эйлер

2. Никлаус Вирт

3. Фон Нейман

4. Блез Паскаль

5. Дейкстра

14. Аппарат теории графов используется при решении …

1. головоломок, игровых задач

2. переборных задач, задач на лабиринтах

3. задач на лабиринтах, шахматной доске

4. задач искусственного интеллекта

5. задач всех перечисленных типов

14. Возникновение теории графов связано с решением задачи …

1. о Кенигсбергских мостах

2. о коммивояжере

3. о Ханойских башнях

4. о шахматных фигурах

5. о фанерном тресте

14. Граф представляет собой структуру, обладающую свойствами …

1. упорядоченности, нелинейности, неоднородности

2. упорядоченности, линейности, однородности

3. упорядоченности, многомерности, однородности

4. неупорядоченности, нелинейности, неоднородности

5. упорядоченности, однородности

14. Примерами графовых моделей могут служить …

1. блок-схема алгоритма, сеть автомобильных дорог

2. сеть автомобильных дорог, локальная сеть в компьютерном классе

3. локальная сеть в компьютерном классе, генеалогическое дерево

4. генеалогическое дерево, блок-схема алгоритма

5. все из перечисленных

14. Основное различие между структурами дерево и граф заключается в том, что …

1. в графе нет листьев

2. в графе нет циклов

3. дерево не имеет циклов

4. дерево не имеет взвешенных ребер

5. дерево не может быть ориентированным

14. В ЭВМ используются системы счисления …

1. восьмеричная, двоичная, десятичная

2. десятичная, двоичная, троичная

3. двоичная, троичная, четверичная

4. шестнадцатеричная, восьмеричная

5. двоичная, восьмеричная, шестнадцатеричная

14. Лишним среди шестнадцатеричных кодов символов {29, 81, 79, 7A, 34} из таблицы ASCII является:

1. 29

2. 81

3. 79

4. 7A

5. 34

14. Для того, чтобы могли быть записаны числа 22, 984, 1010, A219, система счисления должна иметь минимальное основание

1. 10

2. 11

3. 16

4. 2

5. 9

14. 15-ю букву в латинском алфавите определяет выражение:

1. 'A'+chr(14)

2. ord('A')+14

3. chr(ord('A')+14)

4. chr(ord('A'+15)

5. chr('A')+chr(14)

14. Основание системы счисления, в которой справедливы равенства 3+4=7; 3*4=13; 39+29=70, должно быть равно:

1. 10

2. 9

3. 11

4. такой системы не существует

5. 12

14. Если восстановить пропущенные двоичные цифры в примере (вместо знака "*")

1*01₂ + 1**₂ =1*100₂, то получим верное равенство:

1. 1001₂ + 101₂ = 11100₂

2. 1101₂ + 101₂ = 10100₂

3. 1101₂ + 111₂ = 10100₂

4. 1001₂ + 111₂ = 11100₂

5. 1101₂ + 101₂ = 11100₂

14. Этап, на котором устраняются синтаксические ошибки в программе …

1. ввод программы

2. отладка программы

3. тестирование программы

4. сопровождение программы

5. сохранение программы

14. Свойство, не являющееся характеристикой алгоритма …

1. дискретность

2. информативность

3. результативность

4. массовость

5. детерминированность (определённость)

14. Неориентированный граф называется двудольным, если его можно раскрасить …

1. в 2 цвета так, что концы любого ребра - разного цвета;

2. в 3 цвета так, что концы любого ребра – одинакового цвета;

3. в 1 цвет так, что концы любого ребра – разного цвета;

4. в 2 цвета так, что концы любого ребра – одинакового цвета;

5. в 3 цвета так, что концы любого ребра – разного цвета.

14. Под графом понимают:

1. пару (V, E) где E это множество вершин, а V множество пар;

2. пару (V, E) где V это множество вершин, а E множество пар;

3. пару (V, E) где E и V это множество вершин;

4. пару (V, E) где E и V это множество пар;

5. нет правильного ответа.

14. Если в графе все дуги имеют направления, то он называется …

1. связным графом;

2. неориентированным графом;

3. направленным (неориентированным, орграфом);

4. направленным (ориентированным, орграфом);

5. взвешенным графом.

14. Если последовательность ребер соединяет две вершины в орграфе, то она называется …

1. циклом;

2. графом;

3. сетью;

4. цепью;

5. деревом.

14. Если каждому ребру графа приписывается вес (длина), то граф называется:

1. ориентированным

2. неориентированным

3. направленным

4. связным

5. взвешенным

14. Граф, в котором существует цепь между каждой парой вершин, называется …

1. полным;

2. неориентированным;

3. связным;

4. направленным;

5. взвешенным.

14. Граф, в котором проведены все возможные ребра, называется …

1. полным;

2. неориентированным;

3. связным;

4. направленным;

5. взвешенным.

14. Если граф можно разбить на k связных частей, то он называется:

1. полным графом;

2. неориентированным графом;

3. связным графом;

4. k-связным графом;

5. взвешенным графом.

14. Матрица, элемент M[i][j] которой равен 1, если существует ребро из вершины i в вершину j, и равен 0, если такого ребра нет, называется:

1. матрицей смежности;

2. матрицей инцидентности;

3. весовой матрицей;

4. матрицей стоимостей;

5. нет правильного ответа.

14. Матрица, элемент W[i,j] которой равен весу ребра из вершины i в вершину j (если оно есть), или равен ∞, если такого ребра нет, называется:

1. матрицей смежности

2. матрицей инцидентности

3. весовой матрицей

4. матрицей достижимости

5. матрицей связности

14. Матрица размера m*n (m – количество ребер, n – количество вершин), элементы которой определяются по формуле

0, если ребро а не инцидентно вершине А_j

а_ij = 1, если ребро а инцидентно вершине А_j } называется:

1. матрицей смежности

2. матрицей инцидентности

3. весовой матрицей

4. матрицей достижимости

5. матрицей связности

14. К нуль-графам относятся графы:

1

2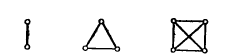

3 *

4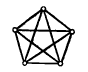

5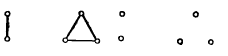

14. Нуль-граф - это граф, который …

1. состоит из вершин с четной степенью

2. состоит из вершин, соединенных ребрами

3. состоит из изолированных вершин, т. е. из вершин, не соединенных ребрами

4. не имеет циклов

5. не имеет вершин нечетной степени

14. Полными графами являются:

1

2

3

4

5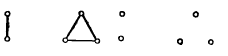

14. Полный граф – это граф, …

1. который состоит из одних вершин

2. который состоит из неизолированных вершин, т. е. из вершин, соединенных ребрами

3. который состоит из одних изолированных вершин, т. е. из вершин, не соединенных никакими ребрами

4. в котором каждая пара вершин соединена ребром

14. Загрузить текст программы в окно редактирования программ можно с помощью клавиши (комбинации клавиш)

1. F1

2. F2

3. F3

4. F5

5. F6

14. Окно вывода результата можно открыть с помощью клавиши (комбинации клавиш)

1. F9

2. Ctrl + F9

3. F3

4. Alt+F5

5. F7

14. Режим пошагового выполнения программы можно осуществить с помощью клавиши (комбинации клавиш)

1. Ctrl + F9

2. Ctrl + F7

3. Alt + F9

4. F7

5. Ctrl + F8

14. Открыть файл в среде TurboPascal можно с помощью клавиши (комбинации клавиш)

1. F1

2. F2

3. F3

4. F9

5. F10

14. Если величина имеет тип Integer, то диапазон изменения ее значений:

1. 0…255

2. 0…65535

3. -32768…32767

4. -128…127

5. 1…256

14. Если величина имеет тип Byte, то диапазон изменения ее значений:

1. 0…255

2. 0…65535

3. -32768…32767

4. -128…127

5. 1…256

14. Если величина имеет тип Word, то диапазон изменения ее значений:

1. 0…255

2. 0…65535

3. -32768…32767

4. -128…127

5. 1…256

57. Если величина имеет тип Shortint, то диапазон изменения ее значений:

1. 0…255

2. 0…65535

3. -32768…32767

4. -128…127

5. 1…256

58. Зарезервированные слова – это слова, …

1. которые находятся в резерве

2. которые можно в случае необходимости использовать в программе

3. за которыми в языке Pascal закреплено определенное смысловое значение и которые нельзя использовать в качестве имен переменных*

4. с помощью которых в Pascal описываются переменные

5. которые в языке программирования Pascal ни в коем случае использовать нельзя

58. Комментарии к программе в языке программирования Pascal – это последовательность слов, …

1. заключенных в круглых скобках.

2. заключенных в фигурных скобках { … }

3. заключенных в квадратных скобках

4. перед которыми стоит служебное слово REM.

5. перед которыми стоят две наклонные черты.

58. Операторные скобки в языке программирования Pascal - это совокупность символов …

1. { }

2. [ ]

3. ( )

4. (* *)

5. begin end;

58. Если объявлен тип Char, то он определяет …

1. Только одну букву.

2. Слово.

3. Строку.

4. Любой набор символов ASCII.

5. Один символ из таблицы кодов ASCII.

58. В качестве разделителя между операторами в языке программирования Pascal используется:

1. “.” точка

2. “,” запятая

3. “;” точка с запятой

4. “:” двоеточие

5. символ «новая строка»

58. Правильным описанием перечисляемого типа является:

1. Type X = 1980 .. 2000;

2. Type X = ( 1979, 1981, 2000);

3. Type X = {1, 4, 5, 6, 8};

4. Type X = [1, 4, 5, 6, 8];

5. Type X = integer;

58. К правильному описанию типа-диапазона (интервального типа) относится:

1. Type X = 1980 .. 2000;

2. Type X = ( 1979, 1981, 2000);

3. Type X = {1, 4, 5, 6, 8};

4. Type X = [1, 4, 5, 6, 8];

5. Type X = integer;

58. К идентификаторам, воспринимаемым компилятором языка Pascal как одна и та же переменная, относятся:

1. Mumi_Trol

2. mumi_trol

3. Mumi_trol

4. MuMi_tRol

5. Mumi Trol

1. 1, 5

2. все, кроме 5

3. все идентификаторы уникальны

4. все

5. все, кроме 3, 5

58. Раздел объявления нестандартных типов начинается с зарезервированного слова …

1. var

2. type

3. const

4. label

5. procedure

67. Возведение в степень А^х в языке программирования Pascal можно организовать с помощью формулы

1. А**x.

2. А^x

3. A*x

4. Exp(x*Ln(a))

5. Нельзя организовать возведение в степень

   68. Ошибка в записи арифметического выражения (для языка Pascal) у:=tan(Х*Х)+ arctan(X); заключается:

1. в языке Pascal нет функции tan()

2. в языке Pascal нет функции arctan()

3. нельзя писать знак «:=»

4. нельзя писать знак «;»

5. строка не содержит ошибок

68. Результатом выполнения заданного фрагмента программы является:

begin а:=5; b:=2; с:=а/b+b/а; write(c); end. является:

1. 2

2. 2.9

3. 4.9

4. 5

5. 7

68. Если задано выражение not(X>100 and Хor not(Xor Х>1), то при Х=5 его значение равно:

1. истина

2. ложь

3. вся числовая ось

4. пустое множество

5. среди ответов A)-D) нет верного

68. Поиск вхождения заданного фрагмента в исходном тексте позволяет выполнить функция …

1. Copy()

2. Length()

3. Pos()

4. ASCII()

5. CHR()

68. Значение Р после выполнения операции логического присваивания P:=(2*2=4) and (3*3=10) равно:

1. 14

2. Истина

3. 0

4. Ложь

5. 1

68. Если значение выражения NOT(XY) or NOT(X=Z) ложно, то значения X,Y, Z равны:

1. X=0; Y=-8; Z=0

2. X=-2;Y=8; Z=-2

3. X=2; Y=0; Z=2

4. X=1; Y=2; Z=3

5. X=3; Y=2; Z=1

68. Значения переменных A и B после выполнения фрагмента программы A:=1; B:=10; A:=A+B; B:=A-B; A:=A-B; равны:

1. A=1, B=10

2. A=10, B=1

3. A=11, B=1

4. A=1, B=1

5. A=11, B=11

75. Если переменные a и b имеют тип Integer, то результаты выполнения операторов a:=b*2 div 2 и a:=b div 2*2 не совпадут для значения b=…

1. 0

2. 2

3. MaxInt

4. Для любых значений b

5. Таких значений нет

76. Если вместо знака "?" подставить одно из выражений, то при х=1 данное логическое выражение станет истинным "?" ((x>0) and (xand "?" ((x>0) or (x

1. "not" и " "

2. " " и " "

3. "and" и " "

4. " " и "and"

5. "not" и "not"

77. Если вместо переменной Х подставить значение Х=1, то истинными будут выражения:

1. not((x>1) and (x

2. (x5)

3. not(x>0) or x

4. not(not(x)) and x

1. все, кроме второго

2. только истинны

3. все истинны

4. первое и третье

5. первое и четвёртое

   78. Если х= - 6.3, то результат выражения writeln(trunc(X*X)+trunc(X+1.8)+2):

1. пустое множество

2. 37

3. 36

4. 37.19

5. 36.19

79 Если дано выражение writeln((21 or 29) and (17 or 24)), то его результат:

1. 25

2. 0

3. 29

4. 17

5. 24

80. Если задана процедура write(2*x+ 5*arctan(m/х)), то при х=2 будет выведен результат:

1. ничего не напечатает

2. напечатает сообщение об ошибке

3. число 4

4. число 6

5. число 5

81 Если идёт k-я секунда суток, то к этому моменту прошло полных часов X и полных минут Y:

1. X:=K DIV 3600; Y:=(K DIV 3600) MOD 60

2. X:=K DIV 3600; Y:=(K MOD 3600) DIV 60

3. X:=K MOD 3600; Y:=(K MOD 3600) DIV 60

4. X:=K DIV 3600; Y:=(K-X*3600) NOD 60

5. X:=K MOD 3600; Y:=(K-X*3600) DIV 60

82. Если дано выражение (ord(chr(ord('8')+1))-ord('0'))+round(cos(sin(0))+3/1.5, то результат:

1. 10

2. 11

3. 12

4. 13

5. выражение содержит ошибку

83. Если a и b - два условия, то из приведённых ниже логических выражений соответствуют высказыванию: "Из двух условий a и b истинно одно и только одно":

1. a or b

2. (a or b) and (not a or not b)

3. a and b

4. a and b or not (a and b)

5. a and not b or b and not a

84. Если a и b - два множества, то из приведённых ниже выражений тождественны выражению (a + b)*(a - b)*(b - a):

1. a-a*b-b

2. a*b

3. a-b

4. [ ]

5. a+b

85. Если дано выражение chr(ord('2')+ord(chr(ord('2')+(ord('2')-ord('1')+1))'3')), то его результат:

1. '3'

2. значение выражения нельзя вычислить

3. '2'

4. false

5. '1'

86. Если a и b - переменные типа Boolean, то значение выражения … всегда равно a:

1. ( a and not a) or (not a and a)

2. not (a or not a)

3. not a and((b or not b) and not a)

1. 1

2. 2

3. 3

4. все выражения

5. ни одно из выражений

87. Если дано выражение (a or b) and (a or c), то тождественными ему являются:

1. a

2. b and c

3. b or c

4. a or (b and c)

5. a and (b or c)

88. Если задано выражение Not((x>0) and (xand not((xor (x>1)), то его результат:

1. вся числовая ось

2. точки х=0 и х=1

3. пустое множество

4. точка х=0

5. отрезок [0;1]

89. Если переменные a и b имеют тип множества, то после упрощения выражение

a*(b-a)+a*(b+a) примет вид:

1. a*b

2. [ ]

3. а

4. 2*a*b

5. нельзя упростить - в выражении есть ошибка

90. Если будет выполнена программа, то результат ее выполнения:

var c: shortint;

begin

c: =1; c: =128*(c+1)-3; writeln(c)

end.

1. -125

2. сообщение об ошибке

3. 0

4. 253

5. -3

91. Если в приведенной программе есть ошибка, то она имеет вид:

Program a1 (input, output);

Var x:integer;

Begin

x := 3; y := 2*x; Writeln( y )

End.

1. Нельзя писать первую строку.

2. После End нельзя ставить точку.

3. После оператора Writeln( y ) пропущен символ точки с запятой.

4. Нельзя писать директиву Input, поскольку нет ввода а с клавиатуры.

5. Не описан тип переменной у.

92. Если в приведенном примере программы есть ошибка, то она имеет вид:

Program a1 (input, output);

Var x, у: integer;

Begin

x := 3; y := x/2; Writeln( y )

End.

1. Нельзя писать первую строку.

2. После End нельзя ставить точку.

3. После оператора Writeln( y ) пропущен символ точки с запятой.

4. Нельзя писать директиву Input, поскольку нет ввода а с клавиатуры.

5. Неверно описан тип переменной у.

93. С помощью фрагмента программы реализован алгоритм:

while (x>y) or (y>z) do

begin

if x>y then begin a:=x;x:=y;y:=a end;

if y>z then begin a:=y; y:=z; z:=a end;

if x>y then begin a:=x;x:=y;y:=a end;

end;

1. поиска максимального значения среди величин z, y, z

2. сортировки трёх величин по убыванию

3. поиска минимального значения среди величин x, y, z

4. сортировки трёх величин по возрастанию

5. обмена значениями величин x и z

94. Условным является оператор:

1. if условие> then s1 else s2

2. while do s

3. repeat s until

4. for then s

5. case s

95. Выражение, тождественное выражению a and b:

1. (a or b) and (not a or not b)

2. not (not a and not b)

3. not (a or b)

4. not (a or (c and b and not c))

5. a and (a and b) and (c or not c)

96. Значение выражения (если это возможно) ord(odd(round(cos(0))+ord('F')-ord('G'))):

1. в записи выражения есть ошибка

2. 0

3. true

4. 1

5. 2

97. Если задано выражение (r : real; b: byte ):b:=ord('8'то его значение равно:

1. 1.000000E+00

2. 1

3. 0

4. 0.000000E+00

5. в записи операторов есть ошибка

98. Если a и b – множества, то тождественными выражению (a+b)*(b+a)*a*b-(a+b) являются:

1. a*b

2. [ ]

3. a+b

4. a*b - b*a

5. a-b

99. Если будет выполнена программа, то ее результатом является значение функции:

const e=0.001;

var x, s, p:real; i: integer;

begin

readln(x); i: =0; s: =1; p: =1;

while abs(p)>e do

begin

i: =i+1; p: =p*(x*x/(2*i*(2*i+1))); s: =s+p

end;

writeln(s)

end.

1. в тексте программы есть ошибки

2. программа зациклится

3. 

4. 

5. 

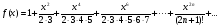
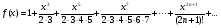
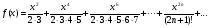
100. Результат выполнения фрагмента программы равен:

P:=x; for k:=3 to n do P:=P*(-x);

1. (-x)ⁿ

2. (-x)^n-1

3. (-1)ⁿx^n-1

4. (-1)ⁿx^n-2

5. x^n-1

101. К операторам цикла, которые можно использовать с шагом, отличным от 1 (-1), относятся:

1. FOR и WHILE

2. FOR и REPEAT

3. FOR …DOWNTO

4. WHILE и REPEAT

5. FOR, WHILE и REPEAT

102. Если дан фрагмент программы, то результат ее выполнения:

var с:integer;

begin

for k:=1 to 5 do

begin

for j:=1 to 3 do i:=i*j; if k>9 then break; end;

writeln(k,' ',i,' 'j);

end.

1. 1244

2. 933

3. 934

4. 1243

5. Сообщение об ошибке

103. Данный фрагмент программы реализует алгоритм

readln(a); m:=0;

repeat

р:=trunc(a/10); m:=m*10+а - р*10; а:= р;

until а=0;

writeln( m);

1. подсчёта суммы цифр натурального числа

2. перестановки цифр натурального числа

3. произведения цифр натурального числа

4. подсчета количества цифр натурального числа

5. удаления первой цифры натурального числа

104. Если будет выполнен фрагмент программы, то ее результатом является

p:=1; for i:=1 to 10 do if i mod 3=0 then p:=p*2; writeln(p);

1. 4

2. 8

3. 10

4. 12

5. 16

105. Результатом выполнения фрагмента программы является:

p:=1;

i:=3; while i

begin

p:=p*2; i:=i+3;

end;

writeln(p);

1. 2

2. 4

3. 6

4. 8

5. 16

106. Переменная Y в результате выполнения фрагмента алгоритма примет значение:

y:=5; x:=0;

while x

begin

y:=y+x; x:=x+2

end;

1. 15

2. 11

3. 9

4. 5

5. 12

107. Переменная s в результате выполнения фрагмента алгоритма примет значение:

s:=0; x:=2;

while x

begin

p:=1; for i:=1 to x do p:=p*2;

s:=s+ p; x:=x+1;

end;

1. 32

2. 28

3. 60

4. 5

5. 65

108. В результате выполнения программы количество повторений тела цикла в алгоритме равно:

m:=36; n:=56;

while mn do

if m>n then m:=m-n else n:=n-m;

1. бесконечное число раз

2. 8

3. 4

4. 6

5. 5

109. Приведенный фрагмент программы реализует алгоритм:

s:=0; k:=1;

repeat

k:=k+2;

s:=s+k*k;

until k>n;

1. вычисления суммы квадратов чётных чисел в промежутке 1…n

2. вычисления суммы квадратов нечётных чисел в промежутке 1…n

3. вычисления суммы квадратов чётных чисел в промежутке 3…n

4. вычисления суммы квадратов нечётных чисел в промежутке 3…n

5. вычисления суммы квадратов чисел в промежутке 3…n

110. Если в программе описаны целочисленные переменные var i, s: integer, то

в результате выполнения фрагмента программы будет выдан результат:

i: =15; s:=0;

while i

begin

s: = s+i; i: = i+16

end;

writeln(s);

1. 60

2. MaxInt

3. -1

4. при выполнении программы произойдёт ошибка

5. программа зациклится и не выведет никакого результата

111 Следующая программа при а=103452 выведет результат:

Var a, p, b: longint; n, i, x: integer;

Begin

Readln(a);

b:=0; p:=1;

repeat

x:=a mod 10; if x mod 2=0 then b:=b+x*p; p:=p*10; a:=a div 10;

until a=0;

write(b);

end.

1. 1042

2. 402

3. 135

4. 24

5. 531

112 Если в примере допущена ошибка, то она имеет вид:

i := 5;

Repeat

S := S +i; i := i+1

Until i > 10;

1. После служебного слова Repeat необходим символ « ; »

2. Внутри цикла пропущены операторные скобки Begin … End;

3. После оператора i := i + 1 пропущен символ « ; »

4. Неверно записано условие после служебного слова Until

5. В приведенном примере ошибок нет.

113 Если в приведенном примере программы есть ошибка, то она имеет вид:

Var x, y: real;

Begin

For x := 1 to 5 do y := x/2;

Writeln (y)

End.

1. После служебного слова Do пропущен символ « ; »

2. После цикла « For » пропущены операторные скобки Begin … End;

3. Переменная цикла «Для» не может быть вещественного типа.

4. После оператора Writeln необходим символ « ; »

5. В приведенном примере нет ошибок.

114 Структурами данных, используемыми в графовых алгоритмах, являются:

1. очередь, стек, массив, список, множество

2. очередь, стек, цикл, развилка

3. массив, строки, списки

4. массивы, строки, матрицы, перестановки

5. сочетания, размещения, строки, списки

115. Структура данных, в которой элементы обрабатываются по правилу «последним пришел – первым вышел», называется:

1. очередью

2. стеком

3. массивом

4. строкой

5. матрицей

115. Структура данных, в которой элементы обрабатываются по правилу «последним пришел – последним вышел», называется:

1. очередью

2. стеком

3. массивом рангов

4. строкой

5. матрицей стоимости

115. Структура данных, в которой хранятся номера вершин-истоков, называется:

     1. очередью

     2. стеком

     3. массивом предков вершин графа

     4. массивом рангов

     5. матрицей стоимости

116. Структура данных, в которой хранятся номера «фронта волны», называется:

     1. очередью

     2. стеком

     3. массивом рангов вершин графа

     4. строкой

     5. матрицей смежности графа

117. Метод восстановления пройденного пути в графе из очереди основан на:

     1. обработке стека номеров вершин

     2. обработке массива предков

     3. обработке очереди «с конца»

     4. просмотра матрицы стоимостей

     5. выдачи массива кратчайших путей

118. При решении задач динамического программирования используются методы:

     1. алгоритм перебора вершин графа в глубину

     2. алгоритм перебора вершин графа в ширину

     3. поиск рекуррентных соотношений

     4. алгоритм перебора вершин графа в ширину, поиск рекуррентных отношений

     5. метод Эйлера

119. При решении задач динамического программирования используются методы:

1. алгоритм перебора вершин графа в глубину

2. алгоритм перебора вершин графа в ширину

3. поиск рекуррентных соотношений

4. построение матрицы стоимостей, поиск рекуррентных отношений

5. метод Эйлера

115. Этап, на котором устраняются синтаксические ошибки в программе:

1. ввод программы

2. отладка программы

3. тестирование программы

4. сопровождение программы

5. сохранение программы

115. К методам оптимизации алгоритма относятся:

1. метод полного перебора

2. метод динамического программирования

3. метод ветвей и границ

4. метод ветвей и границ, метод динамического программирования

5. метод полного перебора, метод ветвей и границ

115. При решении задач на лабиринтах используются методы

1. перебор в глубину, в ширину

2. перебор в ширину, в глубину, рекурсивные, комбинаторные

3. рекурсивные, комбинаторные

4. комбинаторные, рекурсивные, рекуррентные

5. волновой метод

115. Метод перебора клеток лабиринта в ширину носит название

     1. волнового метода

     2. метода лесного пожара

     3. метода проб и ошибок, метода лесного пожара

     4. перебора с возвратом

     5. волнового метода, метода лесного пожара

116. Метод перебора клеток лабиринта в глубину носит название

     1. волнового метода

     2. метода лесного пожара

     3. метода проб и ошибок, метода лесного пожара

     4. перебора с возвратом, метода проб и ошибок

     5. волнового метода, метода лесного пожара

117. Метод перебора вершин в ширину, волновой метод, метод лесного пожара – это методы, используемые при:

     1. поиске пути в графе, лабиринте

     2. поиске кратчайшего пути в графе, лабиринте

     3. поиске дешевого пути в графе, лабиринте

     4. решении задач методом динамического программирования

     5. поиске пути во взвешенном графе

118. Формирование матрицы стоимостей, использование рекуррентных соотношений, использование алгоритма Дейкстры – методы, используемые при:

     1. нахождении дешевого пути во взвешенном графе

     2. нахождении кратчайшего пути в невзвешенном графе

     3. нахождении кратчайшего пути в ориентированном графе

     4. нахождении кратчайшего пути в лабиринте

     5. нахождении дешевого пути во взвешенном графе, лабиринте

119. Алгоритмы Дейкстры, Флойда – алгоритмы поиска:

     1. кратчайшего пути между вершинами графа

     2. кратчайших путей между вершинами графа

     3. путей с максимальной стоимостью

     4. пути с минимальной стоимостью

     5. путей с минимальной суммой весов ребер

120. Алгоритм Эйлера представляет собой алгоритм построения:

1. кратчайшего пути в графе

2. эйлерова цикла в графе

3. гамильтонова цикла в графе

4. построения каркаса графа

5. построения дерева графа

115. Алгоритм построения уникурсальной линии основан на применении алгоритма:

1. Гамильтона

2. волнового метода

3. Эйлера

4. перебора в глубину

5. Дейкстры

115. Алгоритм Флойда является обобщением алгоритма:

1. Прима

2. Эйлера

3. Дейкстры

4. Гамильтона

5. перебора в ширину

115. Алгоритмом построения кратчайших путей между всеми парами вершин графа является:

1. алгоритм Дейкстры

2. алгоритм Эйлера

3. алгоритм Флойда

4. алгоритм перебора вершин графа в глубину

5. алгоритм перебора вершин графа в ширину

115. Алгоритм Дейкстры – это алгоритм построения:

1. кратчайших путей между всеми парами вершин взвешенного графа

2. кратчайших путей между указанной вершиной и всеми остальными вершинами взвешенного графа

3. кратчайших путей в лабиринте

4. кратчайшего пути в графе

5. циклов в графе

115. Алгоритмы Дейкстры, Флойда используются для построения кратчайших путей:

1. во взвешенном графе

2. в ориентированном графе

3. в связном графе

4. в полном графе

5. в двудольном графе

115. Если граф может быть разбит на два пустых подграфа, то такой граф называется:

1. пустым

2. полным

3. двудольным

4. связным

5. несвязным

115. Если граф имеет цикл Эйлера, то такой граф называется:

1. эйлеровым графом

2. полуэйлеровым графом

3. гамильтоновым графом

4. полным графом

5. связным графом

115. Если граф имеет цепь Эйлера, то такой граф называется:

1. эйлеровым графом

2. полуэйлеровым графом

3. гамильтоновым графом

4. полным графом

5. связным графом

115. Если существует путь между всеми парами вершин графа, то в таком случае граф является:

1. достижимым

2. связным

3. полным

4. пустым

5. эйлеровым

115. Если граф является связным, то в таком случае в графе:

1. существует цикл Эйлера

2. существует цепь Эйлера

3. существует путь между каждой парой вершин графа

4. существует гамильтонов цикл

5. существует путь, соединяющий все вершины графа

115. Цикл repeat … until будет продолжаться до тех пор:

1. пока условие не выполняется

2. пока условие выполняется

3. пока не пройдёт заданное количество итераций

4. цикл не выполняется ни разу

5. бесконечный цикл

115. Что Цикл while … do будет продолжаться до тех пор:

     1. пока условие не выполняется

     2. пока условие выполняется

     3. пока не пройдёт заданное количество итераций

     4. цикл не выполняется ни разу

     5. цикл выполняется бесконечное число раз

116. Стандартная процедура GotoXY() выполняет:

1. установку курсора в графическом режиме

2. управление позиционированием курсора в текстовом режиме

3. смещение курсора на позицию X,Y

4. прерывание процесса и переход на метку XY

5. вывод текста в точке X,Y

115. Над элементами типа "множество" в Pascal допустимыми являются операции:

1. объединение, пересечение, дополнение, разность, отрицание

2. объединение, пересечение, дополнение, отрицание, умножение

3. объединение, пересечение, дополнение, разность

4. объединение, пересечение, дополнение

5. объединение, пересечение, разность

115. Над элементами типа string допустимыми являются операции:

1. сложение, вычитание, умножение, конкатенация, отрицание

2. сложение, умножение, конкатенация, отрицание

3. слияние, вычитание, умножение, конкатенация, отрицание

4. слияние, конкатенация, отрицание

5. конкатенация, слияние

115. К логическим операциям не относится:

1. not

2. or

3. mod

4. and

5. xor

115. Если логическое выражение (x>=a) and (xb) принимает значение true, то значение Х:

1. x[a,b]

2. x[a,∞) [b, ∞)

3. x(-∞,a] [b, ∞)

4. x(-∞,b] [a, ∞)

5. x(-∞,a] [b, ∞)

115. Расстоянием от вершины Аi до Аj в графе называют:

1. максимальное число ребер пути

2. минимальное число ребер пути

3. сумму степеней вершин графа

4. количество ребер графа

5. количество вершин графа

115. Расстояние от вершины А_i до А_i в графе считают равным:

1. 0

2. 1

3. -1

4. 2

5. бесконечности

115. Расстояние межу вершинами графа А_i и А_j считают равным бесконечности, если:

1. если пути из А_i в А_i нет

2. если пути из А_i в А_j нет

3. если есть пути из А_i в А_j

4. если есть пути из А_i в А_i

5. нет верного ответа

115. В случае неотрицательного веса дуги графа при нахождении кратчайших путей между заданными вершинами в графе применяется:

1. Алгоритм Флойда

2. Сложный алгоритм

3. Простой алгоритм

4. Алгоритм Дейкстры

5. Алгоритм перебора с возвратом

115. Если граф задан матрицей смежности, то значение величины Sm[i,j] обозначает:

1. ширину ребра

2. высоту ребра

3. длину ребра

4. сумму ребер

5. глубину ребер

115. Если ребра между вершинами взвешенного графа нет, то его длина полагается равной:

1. Sm [i,j] =0

2. Sm [i, j] =1

3. Sm [i, i]

4. Sm [i, i] >=0

5. Sm [i, j] =

115. Если ребра между вершинами невзвешенного графа нет, то его длина полагается равной

1. Sm [i,j] =0

2. Sm [i, j] =1

3. Sm [i, i]

4. Sm [i, i] >=0

5. Sm [i, j] =

115. Если в задаче необходимо найти кратчайшие пути между каждой из пар вершин графа, можно воспользоваться:

1. Алгоритмом Флойда

2. Сложным алгоритмом

3. Простым алгоритмом

4. Алгоритмом Дейсктры

5. Сложным алгоритмом или Алгоритмом Дейсктры

115. Рекурсивный спуск в рекурсивном алгоритме заканчивается, если:

1. на кратчайшем пути между двумя вершинами не окажется промежуточных вершин

2. на кратчайшем пути между тремя вершинами не окажется промежуточных вершин

3. на кратчайшем пути между двумя вершинами окажутся промежуточные вершины

4. на кратчайшем пути между тремя вершинами окажутся промежуточные вершины

5. путь окажется бесконечным

115. Если пути из вершины А_i в вершину А_j во взвешенном графе нет, то:

1. расстояние полагается равным бесконечности

2. расстояние полагается равным 0

3. расстояние полагается равным 1

4. расстояние полагается равным -1

5. расстояние полагается равным Maxint

115. Если для невзвешенного графа Sm [i,j] >=1, то это означает, что:

1. ребра нет, и его длина полагается равной бесконечности

2. ребра нет, и его длина полагается равной 0

3. ребро есть, и его длина полагается равной 1

4. ребро есть, и оно полагается равным -1

5. ребро есть, и оно полагается равным любому положительному числу

115. Под графом понимается

1. совокупность точек и соединяющих их линий

2. совокупность отрезков и соединяющих их точек

3. совокупность вложенных отрезков

4. множество отрезков и точек их пересечения

5. множество пересекающихся отрезков

115. Алгоритм нахождения наикратчайшего расстояния путём выбора самого короткого, ещё не выбранного ребра в графе, называется:

1. Жадным алгоритмом

2. Деревянным алгоритмом

3. Алгоритмом Дейкстры

4. Алгоритмом Флойда

5. Алгоритмом Эйлера

115. Эйлеров цикл в графе существует тогда и только тогда, когда:

1. граф связный

2. граф связный и все его вершины имеют нечетные степени

3. граф связный и все его вершины имеют четные степени

4. граф несвязный и все его вершины имеют четные степени

5. граф несвязный и все его вершины имеют нечетные степени

115. Если граф связный, и все его вершины имеют четные степени, то граф имеет:

1. цикл с предусловием

2. Эйлеров цикл

3. цикл с постусловием

4. Гамильтонов цикл

5. цикл с параметрами

115. «Деревянный алгоритм» может ошибаться:

1. менее чем в 2 раза

2. менее чем в 4 раза

3. более чем в 2 раза

4. более чем в 4 раза

5. ни разу

115. Алгоритм, который может ошибаться менее чем в 2 раза

1. жадный алгоритм

2. деревянный алгоритм

3. алгоритм Дейкстры

4. алгоритм Флойда

5. алгоритм Эйлера

115. К методам решения задачи коммивояжера относятся:

1. метод Анищенко

2. метод Литтла

3. метод Хука – Дживса

4. метод Нелдера – Мида

5. метод Дейкстры

115. Метод Анищенко реализует:

1. метод ветвей и границ

2. метод градиентного спуска

3. метод решения задачи коммивояжера

4. метод покоординатного спуска

5. метод полного перебора

115. К методам оптимизации алгоритма относятся:

1. метод полного перебора

2. метод динамического программирования

3. метод ветвей и границ

4. метод ветвей и границ, метод динамического программирования

5. метод полного перебора, метод ветвей и границ

115. При решении задач на лабиринтах используются методы:

1. перебор в глубину

2. перебор в ширину, в глубину

3. рекурсивные, комбинаторные

4. комбинаторные, рекурсивные, перебор в глубину

5. перебор в глубину, в ширину, рекурсивные, комбинаторные

115. Структуры данных, используемые в графовых алгоритмах:

1. очередь, стек, массив, список, множество

2. очередь, стек, цикл, развилка

3. массив, строки, списки

4. массивы, строки, матрицы, перестановки

5. сочетания, размещения, строки, списки

115. Этап, на котором устраняются синтаксические ошибки в программе

1. ввод программы

2. отладка программы

3. тестирование программы

4. сопровождение программы

5. сохранение программы

115. Свойство, не являющееся характеристикой алгоритма:

1. дискретность

2. информативность

3. результативность

4. массовость

5. детерминированность (определённость)

115. К свойствам информации относятся:

1 достоверность, конечность, массовость, полнота

2 конечность, массовость, полнота, ясность

3 массовость, полнота, ценность, актуальность

4 полнота, ценность, достоверность, актуальность, ясность

5 ценность, актуальность, ясность, сложность

115. Сколько раз повторяется тело цикла в алгоритме:

m:=36; n:=56;

while mn do

if m>n then m:=m-n else n:=n-m;

1. бесконечное число раз

2. 8

3. 4

4. 6

5. 5

115. Значение Р после выполнения операции логического присваивания

P:=(2*2=4) and (3*3=10)

1. 14

2. истина

3. 0

4. ложь

5. 1

115. К реке подошли два мальчика и один взрослый. У берега они увидели лодку, вмещавшую либо двух мальчиков, либо одного взрослого. Если каждая поездка через реку (в одну сторону) занимает 20 минут, то какое минимальное время потребуется на переправу:

1. 40 минут

2. 60 минут

3. 1 час 40 минут

4. 1 час 20 минут

5. 20 минут

115. Если идёт k-я секунда суток, то сколько полных часов X и полных минут Y прошло к этому моменту:

1. X:=K DIV 3600; Y:=(K DIV 3600) MOD 60

2. X:=K DIV 3600; Y:=(K MOD 3600) DIV 60

3. X:=K MOD 3600; Y:=(K MOD 3600) DIV 60

4. X:=K DIV 3600; Y:=(K-X*3600) NOD 60

5. X:=K MOD 3600; Y:=(K-X*3600) DIV 60

115. Если выражение NOT(XY) or NOT(X=Z) будет ложным, то значения X, Y, Z равны:

1. X=0; Y=-8; Z=0

2. X=-2;Y=8; Z=-2

3. X=2; Y=0; Z=2

4. X=1; Y=2; Z=3

5. X=3; Y=2; Z=1

115. Оператор цикла, тело которого выполняется как минимум один раз независимо от значения параметра цикла:

1. WHILE

2. REPEAT

3. FOR X=A TO B DO

4. FOR X=B DOWNTO A DO

5. IF THEN

115. Значения переменных A и B после выполнения фрагмента программы:

A:=1; B:=10; A:=A+B; B:=A-B; A:=A-B;

1. A=1, B=10

2. A=10, B=1

3. A=11, B=1

4. A=1, B=1

5. A=11, B=11

115. Минимальное основание системы счисления, в которой могут быть записаны числа 22, 984, 1010, A219:

1. 9

2. 10

3. 11

4. 16

5. 2

   181. Основание системы счисления, в которой верны равенства: 3+4=7; 3*4=13; 39+29=70

1. 10

2. 9

3. 11

4. такой системы не существует

5. 12

182 Восстановите двоичные цифры в примере: 1*01₂ + 1**₂ =1*100₂

1. 1001₂ + 101₂ = 11100₂

2. 1101₂ + 101₂ = 10100₂

3. 1101₂ + 111₂ = 10100₂

4. 1001₂ + 111₂ = 11100₂

5. 1101₂ + 101₂ = 11100₂

183. Если ученик пересказывает услышанное, то при этом учеником выполняются информационные процессы:

1. Прием и передача

2. Прием и обработка

3. Прием, обработка и хранение

4. Прием, хранение и отправление.

5. Прием, обработка, хранение и передача

183. Слово «информатика» в восьмиразрядной кодировке имеет объем информации:

1. 11 бит

2. 11 бод

3. 11 байт

4. 11 Кбайт

5. 11 Мбайт

183. Происхождение слова «алгоритм» связано с фамилией ученого:

1. Евклид

2. Аль-Хорезми

3. Декарт

4. Коши

5. Пифагор

183. Автором самого древнего алгоритма является:

1. Декарт

2. Пифагор

3. Евклид

4. Герон

5. Гаусс

183. Слова, смысл и способ употребления которых задан раз и навсегда, называют:

1. Командами

2. Простыми словами

3. Служебными словами

4. Составными словами

5. Алгоритмическими конструкциями

183. Аргументами алгоритма называются величины, …

1. являющиеся результатами алгоритма

2. не являющиеся исходными данными алгоритма

3. являющиеся исходными данными алгоритма

4. не являющиеся ни входными, ни выходными данными

5. используемые для промежуточных вычислений

183. Условия, состоящие только из одного отношения между величинами, называются:

1. Одиночными

2. Простыми

3. Одноуровневыми

4. Составными

5. Многоуровневыми

183. Условия, состоящие из двух и более отношений, соединённых логическими связками, называются:

1. Простыми

2. Сложными

3. Составными

4. Многоуровневыми

5. Одиночными

183. Алгоритмы, целиком используемые в составе других алгоритмов, называются:

1. Разветвляющимися

2. Подчинёнными

3. Вспомогательными

4. Второстепенными

5. Циклическими

183. Слово, в котором нет символов, называется:

1. Нулевым

2. Пустым

3. Коротким

4. Машинным словом

5. Символом

183. Число символов в слове называется:

1. Глубиной слова

2. Шириной слова

3. Длиной слова

4. Расширением слова

5. Идентификатором слова

183. Результат выполнения алгоритма K=a mod 10, z=k+c, при a=123, b=345, c=456:

1. 456

1. 459

2. 345

3. 123

4. 579

183. Первоначальный смысл слова «компьютер»:

1. электронный аппарат

2. вид телескопа

3. электронно-лучевая трубка

4. человек, производящий расчёты

5. электронно-вычислительное устройство

183. Основоположником математической логики считается:

1. Чарльз Беббидж

2. Готфрид Вильгельм Лейбниц

3. Блез Паскаль

4. Джордж Буль

5. Джон фон Нейман

183. Основоположником двоичной системы счисления является:

1. Чарльз Беббидж

2. Готфрид Вильгельм Лейбниц

3. Блез Паскаль

4. Джордж Буль

5. Джон фон Нейман

183. Первые мониторы в ЭВМ появились:

1. в первом поколении

2. во втором поколении

3. в третьем поколении

4. в четвёртом поколении

5. в пятом поколении

183. Основные этапы решения задачи на ЭВМ:

1. идентификация, концептуализация, формализация, выполнение, тестирование и опытная эксплуатация

2. постановка, моделирование, разработка алгоритма, программирование, выполнение, анализ результатов

3. анализ, алгоритмизация, программирование, выполнение и тестирование

постановка, формализация, выполнение, тестирование

4. математическое моделирование, программирование, выполнение, анализ результатов

5. моделирование, алгоритмизация, программирование

183. Этап формализации задачи означает:

1. построение математической модели задачи

2. построение алгоритма решения задачи

3. запись алгоритма на формальном языке

4. тестирование работоспособности программы

5. анализ полученных результатов