Слайд 1ВВЕДЕНИЕ В БАЙЕСОВСКИЕ СЕТИ
Алгоритмы для Интернета, ИТМО & СПбГУ С.-Петербург, 26 октября 2006 Рук. семинара Ю.М. Лифшиц
Логико-вероятностная модель баз фрагментов знаний с неопределенностью
Александр Львович Тулупьев ведущий научный сотрудник лаборатория прикладной информатики Санкт-Петербургский институт информатики и автоматизации РАН вице-президент Российской ассоциации нечетких систем и мягких вычислений ALT@iias.spb.su Александр Владимирович Сироткин аспирант лаборатория прикладной информатики Санкт-Петербургский институт информатики и автоматизации РАН avs@iias.spb.su
Слайд 2ПЛАН
БС — что это БС — праксис и генезис Вероятностная логика Фрагменты знаний (ФЗ) Алгебраические байесовские сети Байесовские сети доверия БС — дидактическое применение БС — монография
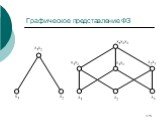
Слайд 3
Слайд 4Идеологическое определение
Байесовские сети --- это графические структуры для представления вероятностных отношений между большим количеством переменных и для осуществления вероятностного вывода на основе этих переменных.
Learning Bayesian Networks Neapolitan R.E., 2004
Слайд 5Уточнение-1
Предположение, лежащее в основе любой вероятностной сети, заключается в том, что, в то время как общая проблема чересчур сложна для применения наивных методов вычисления и обновления вероятностей…, отдельные клики… имеют приемлемый, разумный размер…
Probabilistic Networks and Expert Systems Cowell R.G. et al., 2004
Слайд 6Уточнение-2
…В частности, мы предполагаем, что можем производить (пользуясь, например, «грубой силой», т.е. подходом по определению) любые желаемые операции, такие, как маргинализацию или нормировку, внутри любой клики, но необязательно непосредственно для всей сети сразу…
Слайд 7Уточнение-3
Наша цель --- использовать структуру сети для того, чтобы распространить такие вычисления на полный набор переменных.
Слайд 8Цель ---
представить распределение вероятностей (или их семейство) над (большим числом) переменных, в общем виде выглядящее как
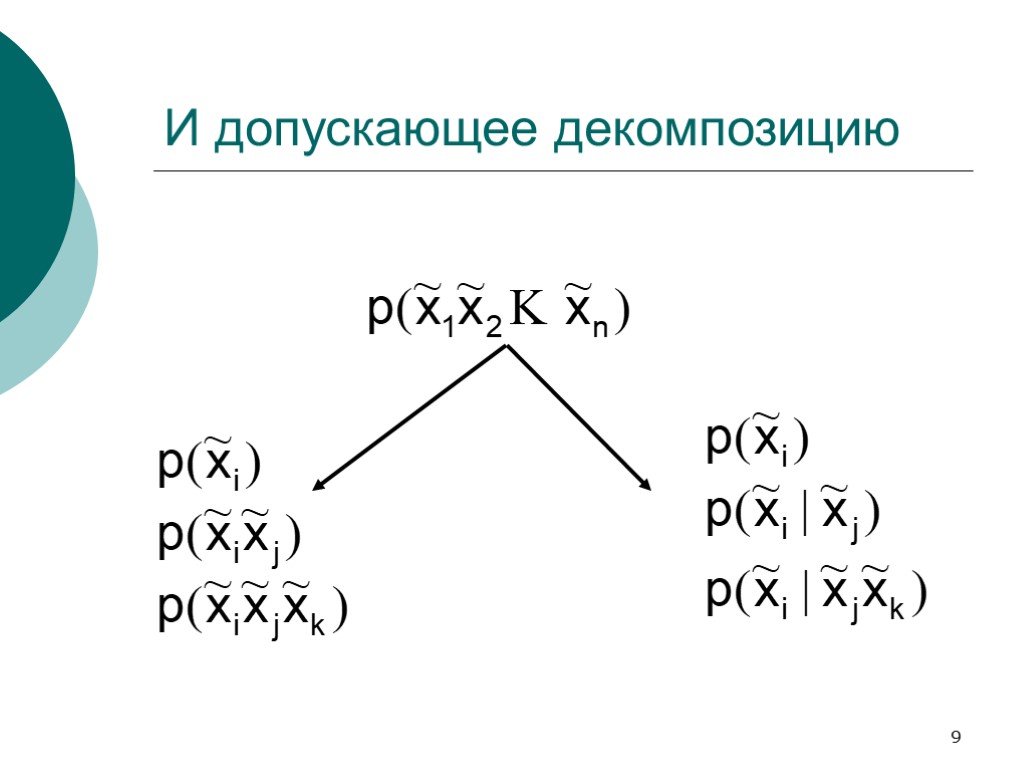
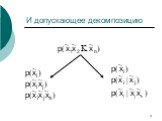
Слайд 9И допускающее декомпозицию
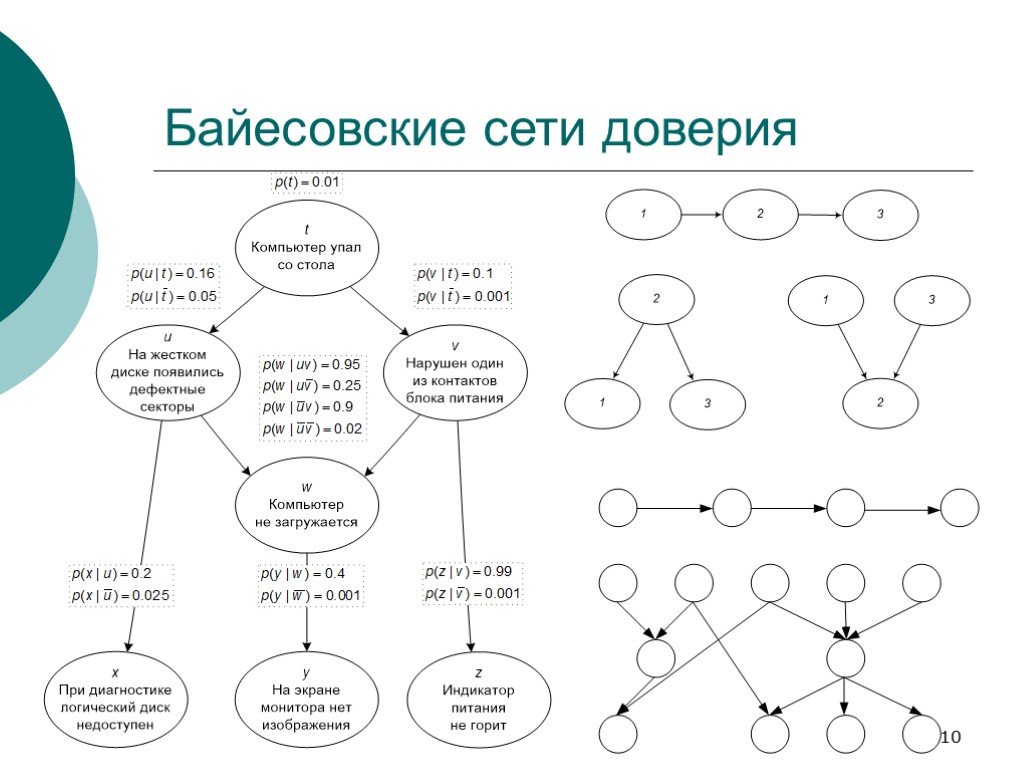
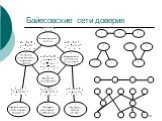
Слайд 10Байесовские сети доверия
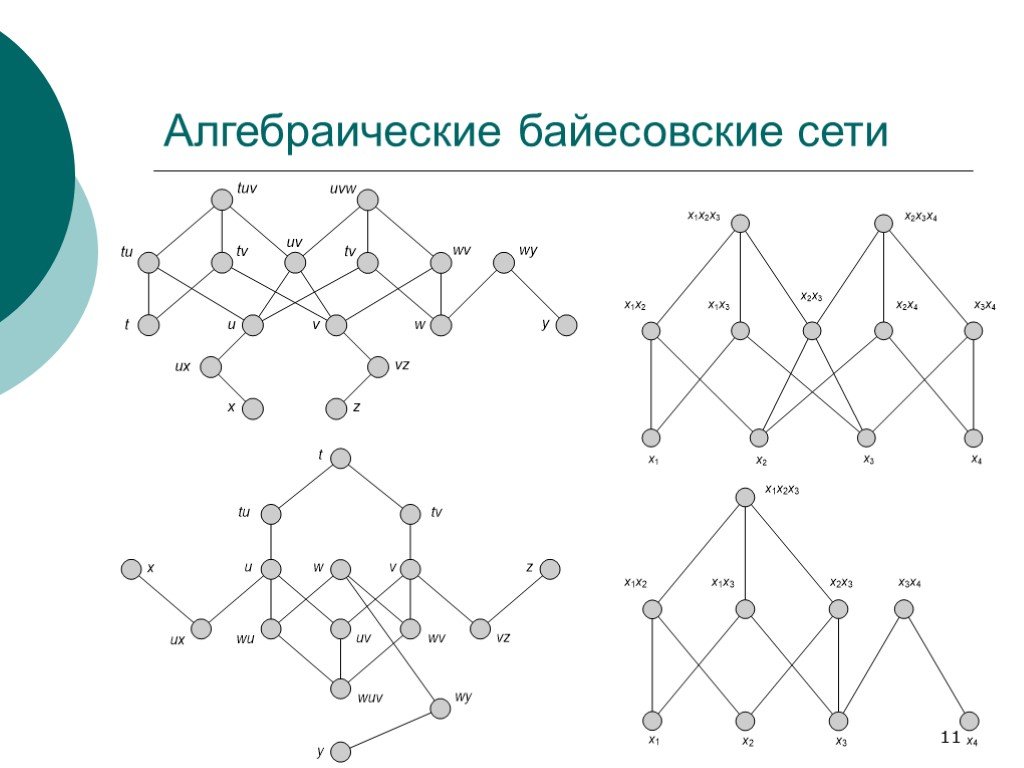
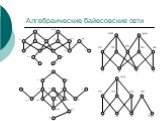
Слайд 11Алгебраические байесовские сети
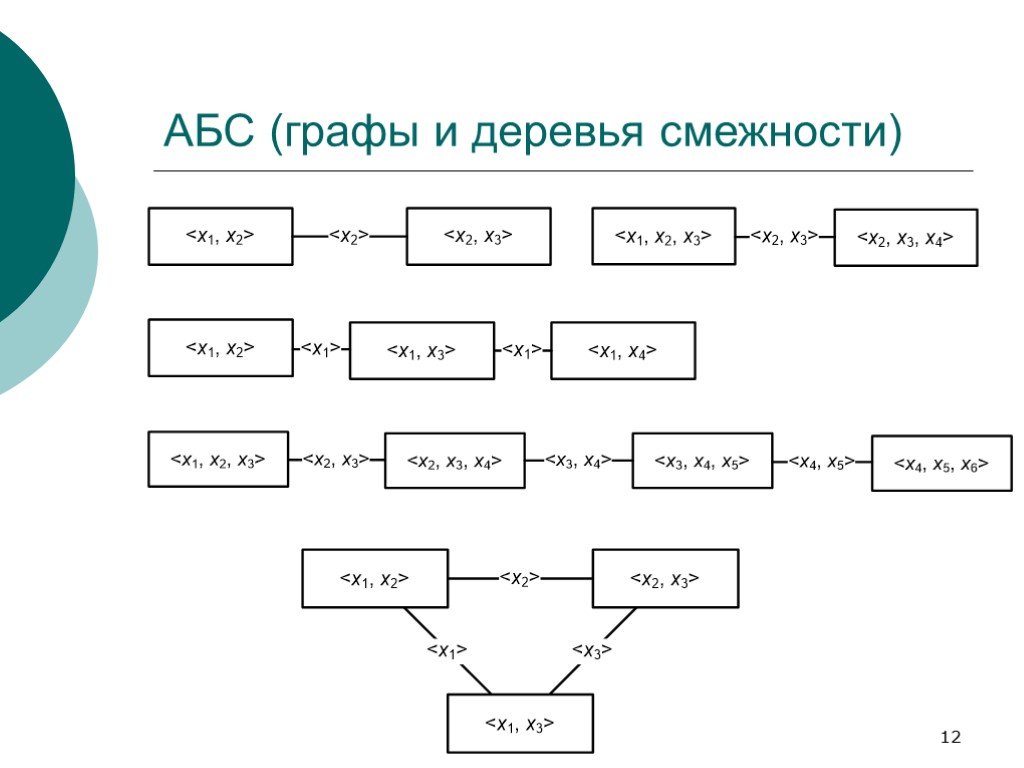
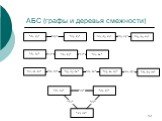
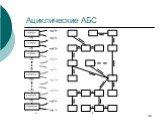
Слайд 12АБС (графы и деревья смежности)
Слайд 13
Слайд 14Почему БС востребованы
ИИ (МВ): знания с неопределенностью, фрагменты знаний, базы фрагментов знаний Статистика: много переменных, связи всех со всеми неописуемые и неоцениваемые, зато отдельные скопления можно неплохо охарактеризовать Техника: декомпозируемость систем, знание свойств элементов и связей между ними
Слайд 15Что предшествовало
Анализ родословных для поиска источника и путей передачи генетических аномалий. Представление результатов статистических наблюдений, когда наблюдаемых переменных очень много, но их удается разбить на условно независимые наборы.
Слайд 16БС применяются в медицине
Для быстрой постановки диагноза, чтобы выбрать правильное учреждение для госпитализации Для дифференциальной диагностики заболеваний, симптоматические проявления которых сходны [но не совпадают полностью]
Слайд 17БС применяются в технологических процессах
Для диагностики отказов и дефектов В драйверах принтеров Для анализа результатов тестирования ПО Для оптимизации запросов в БД Для представления результатов data mining
Слайд 18БС применяются в научных исследованиях
Диагностика концентрации уровня кислорода в озере (PhD Thesis!) Геномика и биоинформатика Все то же представление результатов статистической обработки
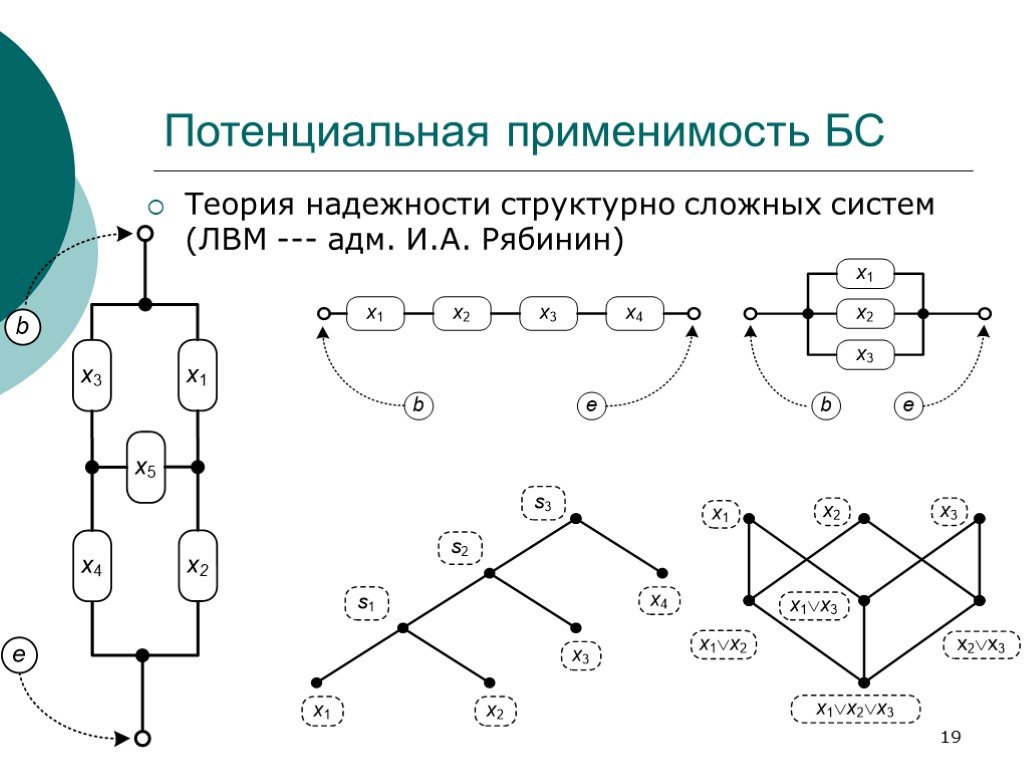
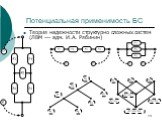
Слайд 19Потенциальная применимость БС
Теория надежности структурно сложных систем (ЛВМ --- адм. И.А. Рябинин)
Слайд 20БС в учебном процессе
Подробнее --- немного позже. Основное Комбинирование и актуализация знаний из нескольких дисциплин; Все объекты и предметы исследования «под рукой»; Полигон для применения программных технологий.
Слайд 21Немного об истории
Логика (от Аристотеля и раньше); Вероятностная логика (от Дж. Буля и позже); в ИИ удачно ввел Н. Нильссон в 1986; различные формализации, мы пользуемся Хальперном, Фагином и Меггиддо; Байесовские сети (БСД – Дж. Пиэрл, АБС – В.И. Городецкий), еще и марковские сети (???); история этим не исчерпывается; смежные дисциплины...
Слайд 22Немного об особенностях
Очень большой упор на графическое представление отношений независимости и условной независимости. Стремление избежать обсуждения тех проблем, решения которых они не знают (подмена циклов последовательностью фрагментов знаний, …) А нам бы о представлении данных хотелось бы поговорить побольше, непротиворечивость посмотреть, алгоритмы вывода выписать и сделать понятными, на доступные программные технологии опереться.

Слайд 23БСД: литература
Статьи Pearl J. (1985). How to Do with Probabilities what People Say You Can't. Artificial Intelligence Applications. Ed. Weisbin C.R., IEEE, North Holland, pp. 6--12. Pearl J. (1986). Fusion, Propagation, and Structuring in Belief Networks. Artificial Intelligence, vol. 29. Elsevier Science Publishers B.V., North Holland, pp. 241--288. Pearl J. (1986a). Constraint-Propagation Approach to Probabilistic Reasoning. Machine Intelligence & Pattern Recognition (Uncertainty in Artificial Intelligence). Eds. Kanal L.N., Lemmer J.F. Vol. 4, Elsevier Science Publishers B.V., North Holland, pp. 357--369. Pearl J. (1986b). On Evidentional Reasoning in Hierarchy of Hypotheses. Artificial Intelligence, vol. 28. Elsevier Science Publishers B.V., North Holland, pp. 9--15. Pearl J. (1986c). Distributed Revision of Composite Beliefs. Artificial Intelligence, vol. 33. Elsevier Science Publishers B.V., North Holland, pp. 173--215. Монографии Pearl J. (1988). Probabilistic Reasoning in Intelligent Systems. Morgan Kaufmann Publishers, 552 pp. Pearl J. (2000). Causality: Models, Reasoning, and Inference. Cambridge University Press, 386 pp. Jensen F.V.(2001). Bayesian Networks and Decision Graphs. Springer-Verlag, NY. 268 pp. Korb K.B., Nicholson A.E. (2004). Bayesian Artificial Intelligence. Chapman and Hall/CRC, 364 pp. Kyburg H.E. Jr. (2001). Uncertain Inference. Cambridge University Press, 298 pp. Lauritzen, S. L. (1996). Graphical Models, Oxford University Press, Oxford, 1996. Neapolitan R.E. (2004). Learning Bayesian Networks. Pearson Prentice Hall, 674 pp. Nilsson N.J. (1998). Artificial Intelligence: A New Synthesis. Morgan Kaufmann Publishers, 514 pp.

Слайд 24АБС: литература
Gorodetsky V.I., Drozdgin V.V., Jusupov R.M. Application of Attributed Grammar and Algorithmic Sensitivity Model for Knowledge Representation and Estimation // Artificial Intelligence and Information, Control Systems of ROBOTSA. North Holland, Elsevier Science Publ., 1984. pp. 232--237. Городецкий В.И. Байесовский вывод. АН СССР, ЛИИАН, Препринт № 149. Л., 1991. Городецкий В.И. Алгебраические байесовские сети --- новая парадигма экспертных систем // Юбилейный сборник трудов институтов Отделения информатики, вычислительной техники и автоматизации Российской Академии наук, т. 2. М., РАН, 1993. с. 120--141. Городецкий В.И., Тулупьев А.Л. Формирование непротиворечивых баз знаний с неопределенностью // Известия РАН. Серия "Теория и системы управления». 1997. №5. Тулупьев А.Л. Алгебраические байесовские сети. Теоретические основы и непротиворечивость. СПб.: СПИИРАН, 1995. 76 с. Тулупьев А.Л. Алгебраические байесовские сети. Логико-вероятностный подход к моделированию баз знаний с неопределенностью. СПб.: СПИИРАН, 2000. 292 с. Тулупьев А.Л., Николенко С.И., Сироткин А.В. Байесовские сети: логико-вероятностный подход. СПб.: Наука, 2006. 607 с.

Слайд 25Веб-сайты
БСД: стоит начинать с www.auai.org АБС: сайт в разработке, можно периодически проверять www.spiiras.nw.ru (а пока пользоваться Зеленой книгой)
Слайд 26
Слайд 27БА пропозициональных формул
Универсум, множество атомов, множество булевских переменных, Множество атомарных пропозиций…
Алгебра пропозициональных формул, построенных над заданным универсумом.
Фактор-алгебра классов тождественных пропозициональных формул. Как правило, далее эквивалентные формулы не различаются. В частности, вероятности истинности эквивалентных формул будут совпадать.
true или 1 --- тождественная истина, константа false или 0 --- тождественная ложь, константа, (f) --- истинностное означивание пропозициональной формулы f.
Слайд 28Аргументное место (литерал)
Аргументное место или литерал. Используется как обозначение означивания атомарной формулы x или как скользящий индекс.
Внутри одной и той же формулы означивания одного и того же аргументного места совпадают. Возможные несовпадения оговариваются отдельно.
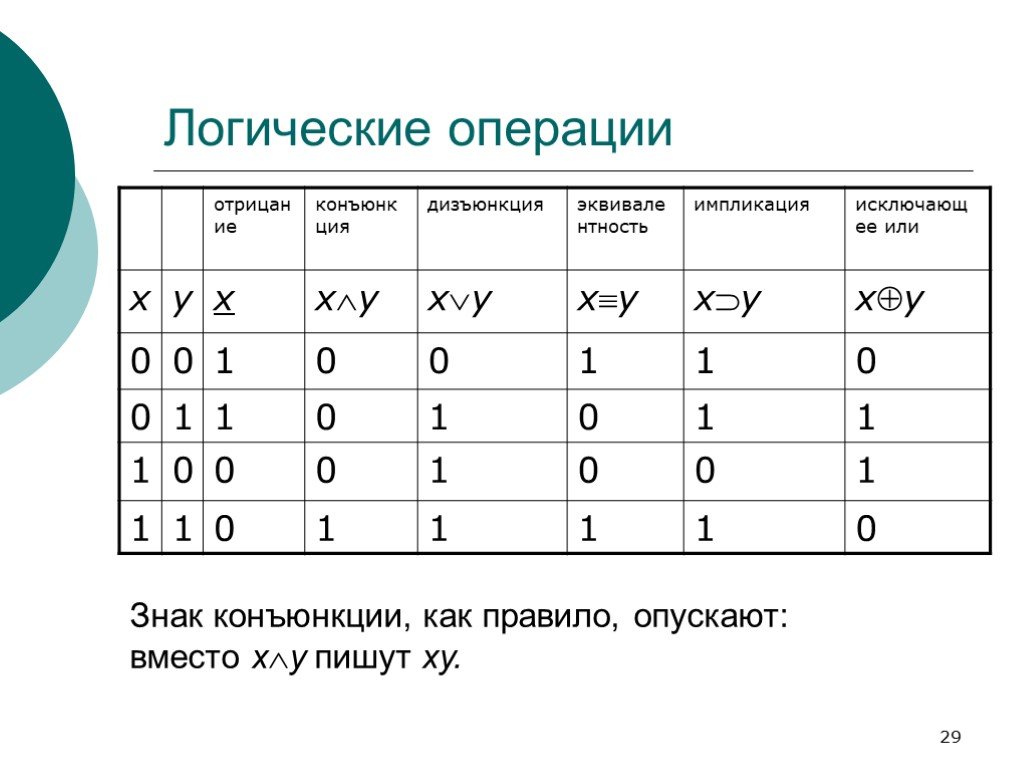
Слайд 29Логические операции
Знак конъюнкции, как правило, опускают: вместо xy пишут xy.
Слайд 30Кванты
Пусть нам задан набор атомов
Квантом называется конъюнкция, в которую входят все атомы из набора. Каждый атом входит с одним из означиваний: либо положительным либо отрицательным.
Пример записи кванта, краткой и полной.
Обозначение множества квантов:
Пример:
Слайд 31Конъюнкты
Конъюнктом называется конъюнкция положительно означенных атомов из набора. В эту конъюнкцию атом либо входит, либо вообще не входит. Один положительно означенный атом тоже является конъюнктом. Пустая конъюнкция (пустой конъюнкт) эквивалентен тождественной истине.
--- примеры конъюнктов.
--- краткая запись конъюнкта.
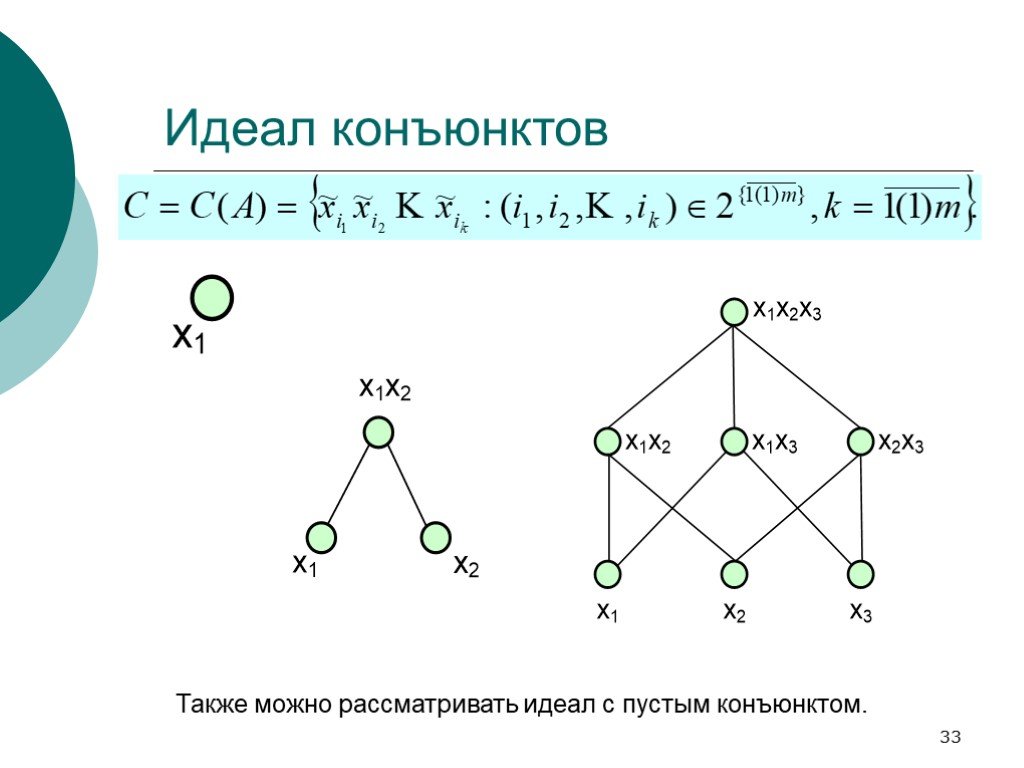
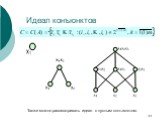
Слайд 33Идеал конъюнктов
Также можно рассматривать идеал с пустым конъюнктом.
Слайд 34Особенности идеала
Множество всех непустых конъюнктов над заданным набором атомов --- идеал; Множество всех (все непустые и один пустой) конъюнктов над заданным набором атомов --- идеал; Непустое пересечение идеалов --- идеал.
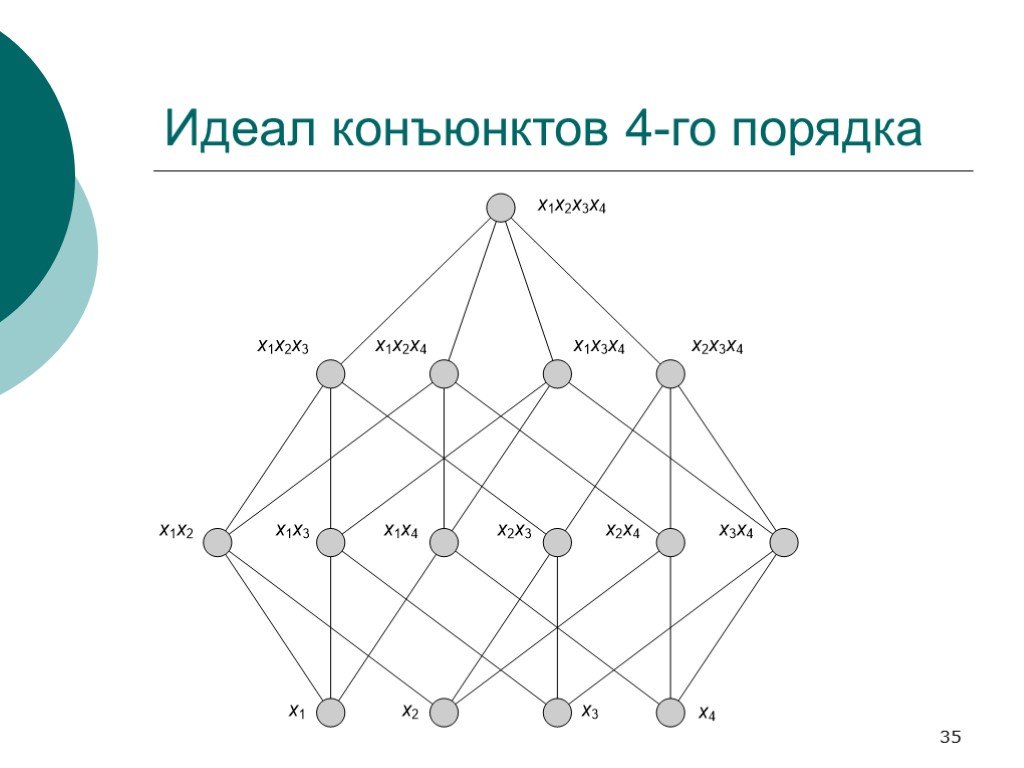
Слайд 35Идеал конъюнктов 4-го порядка
Слайд 38Вероятность истинности
Подход по Н. Нильссону (1986 г.) Более глубокая формализация дана в работах коллектива Фагина, Хальперна, Миггидо (пригодна для рассуждений об оценках сложности) Другие глубокие формализации Спор о приоритетах (de Finetti…) Дж. Буль --- тоже писал о вероятности пропозиции
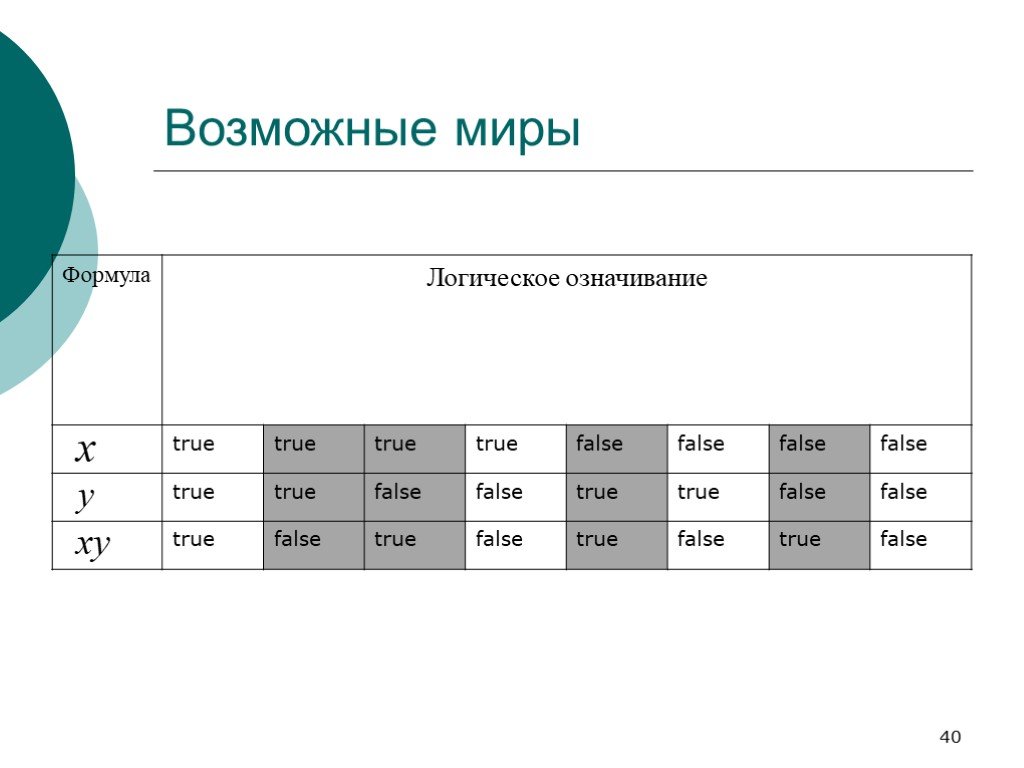
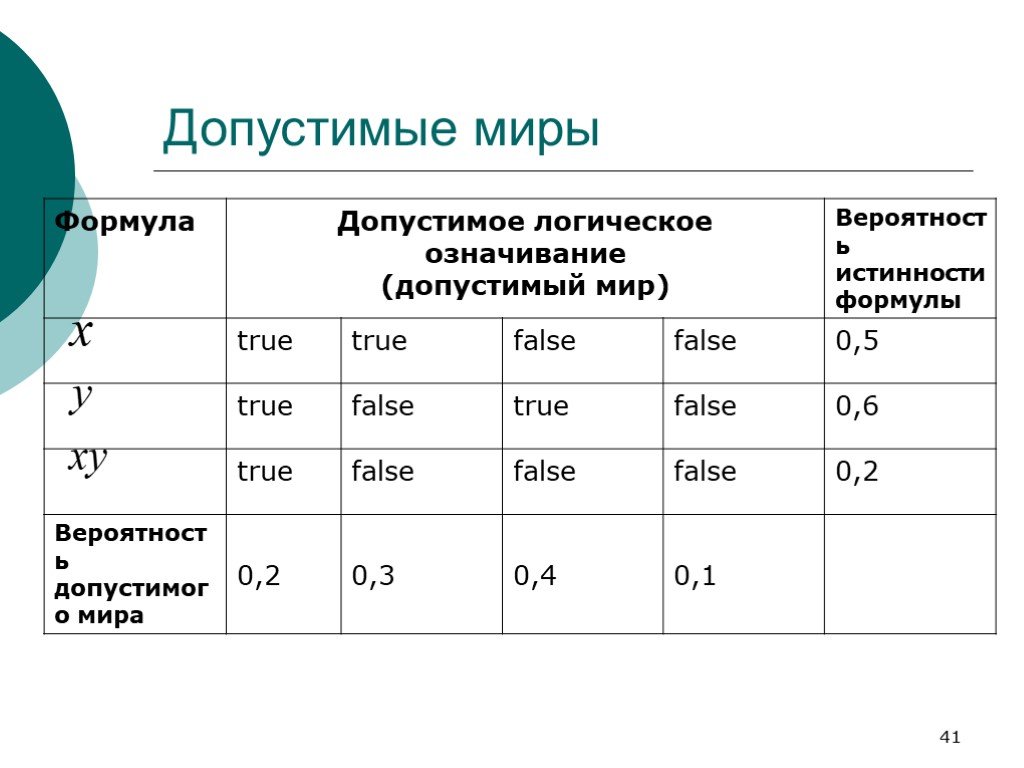
Слайд 42Вероятность пропозиции
В рамках подхода Н. Нильссона мы рассуждаем о вероятности истинности пропозиции; Для краткости говорят вероятность пропозиции
Слайд 43
Слайд 44КВАНТЫ: Множество элементарных событий
Слайд 45ВЕРОЯТНОСТЬ ПРОПОЗИЦИИ
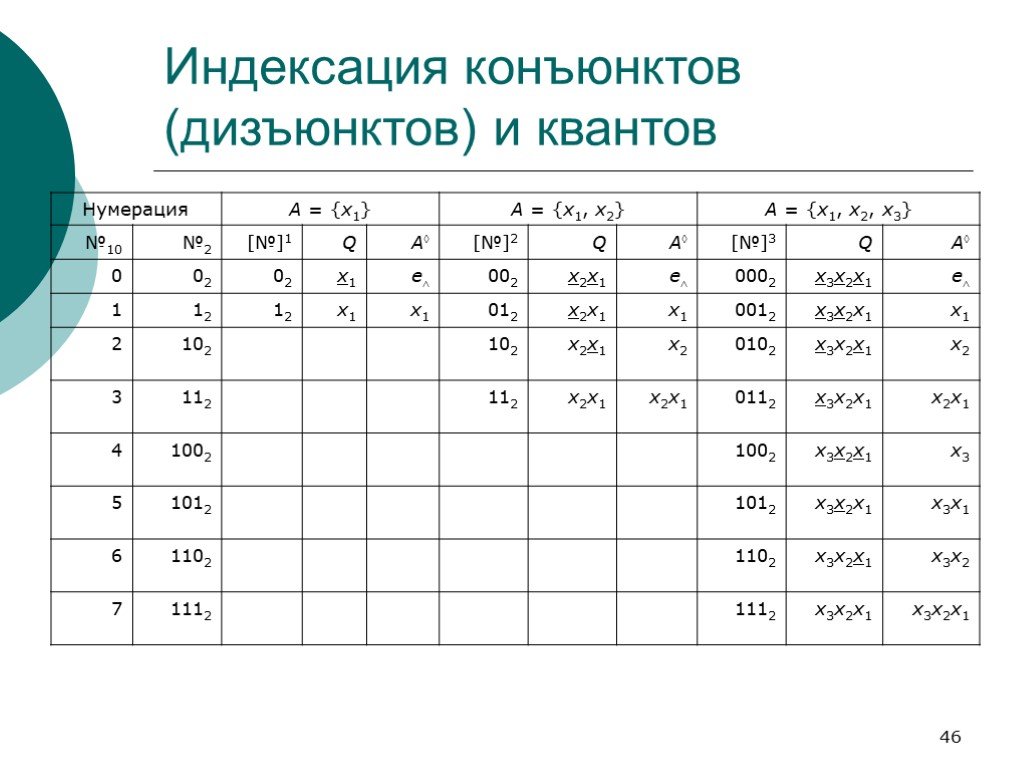
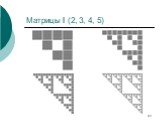
Слайд 46Индексация конъюнктов (дизъюнктов) и квантов
Слайд 47Случайные бинарные последовательности
Слайд 48Базовые понятия ТВ на языке СБП
Слайд 49Кванты и вероятность истинности
Слайд 50Конъюнкты и вероятность истинности
Слайд 51Вероятности квантов и конъюнктов
Связи между наборами квантов и конъюнктов будет обсуждаться ещё неоднократно, поскольку кванты формируют множество элементарных событий, а конъюнкты --- идеал, образующий одну из моделей фрагмента знаний.
Слайд 52Интервальная вероятность конъюнкции
Оценки вероятностей не могут быть произвольно назначены. Вероятности истинности пропозициональных формул находятся в определенных отношениях. Вместе с тем, по точечным оценкам вероятностей одних формул даже в простейших случаях не всегда удается восстановить точечные оценки вероятностей других формул (без привлечения дополнительных предположений).
--- дано.
Слайд 53Modus ponens
И в этом случае даже из точечных оценок вероятностей в антецеденте будут получаться, как правило, интервальные оценки вероятностей в консеквенте. Кроме того, некоторые сочетания оценок в антецеденте будут противоречить аксиоматике вероятностной логики.
Слайд 54
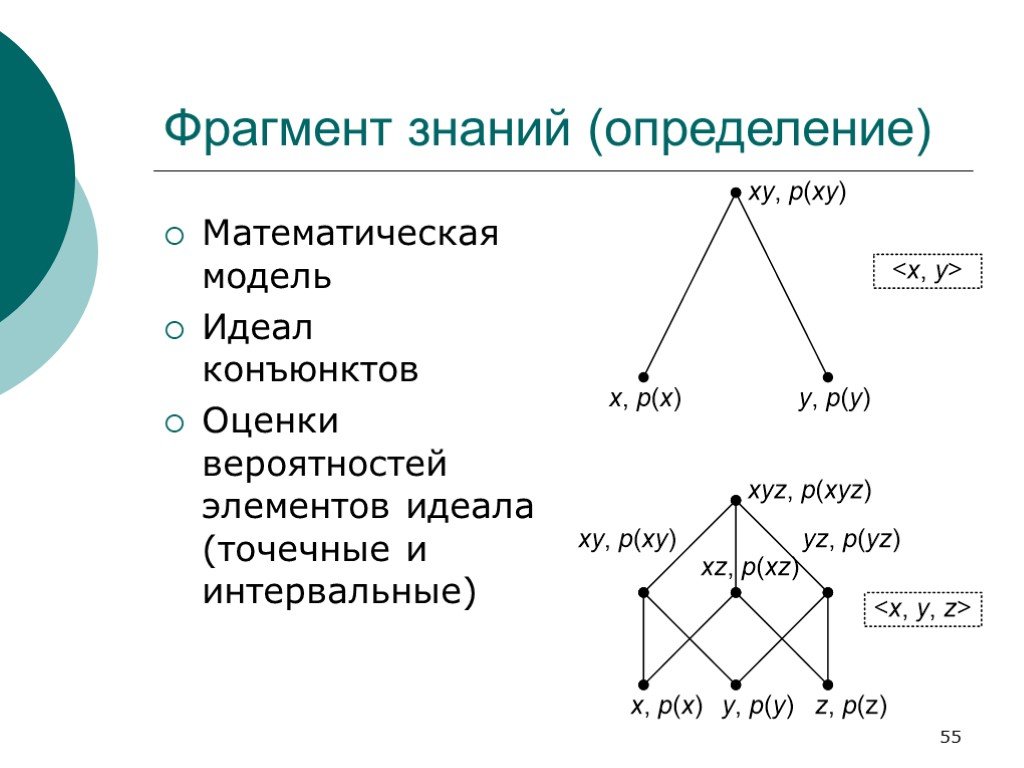
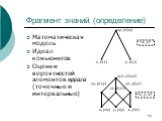
Слайд 55Фрагмент знаний (определение)
Математическая модель Идеал конъюнктов Оценки вероятностей элементов идеала (точечные и интервальные)
Слайд 56ФЗ: Brute Force Calculations
Поддержание непротиворечивости Априорный вывод Апостериорный вывод Вывод оценок чувствительности Объемлющая непротиворечивость Линейные комбинации ФЗ ...
Слайд 57«Точечная» непротиворечивость
p(x)=0.4 p(x)=0.6 непротиворечиво (согласовано, совместно)
p(x)=0.7 p(x)=0.6 противоречиво (несовместно)
Слайд 58«Интервальная» непротиворечивость
p(x)=[0.4;0.5] p(x)=[0.5;0.6] непротиворечиво (согласовано, совместно)
p(x)=[0.7;0.8] p(x)=[0.5;0.6] противоречиво (несовместно) p(x)=[0.3;0.5] p(x)=[0.4;0.6] непротиворечиво (не согласовано, совместно)
Слайд 59Непротиворечивость ФЗ (.)
Преобразовать вероятности на конъюнктах в вероятности на квантах; Проверить соответствие вероятностной аксиоматике получившихся оценок на квантах
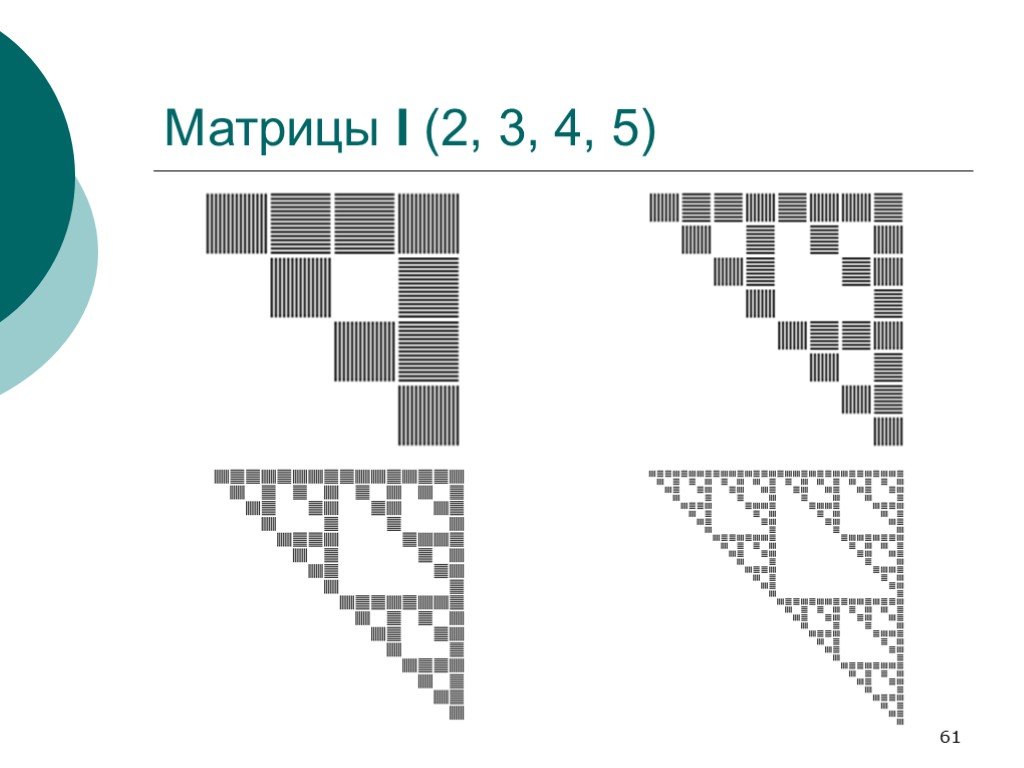
Слайд 60Матрицы In и Jn
Матрицы преобразования вектора вероятностей конъюнктов в вектор вероятностей квантов и наоборот строятся как прямое произведение матриц Кронекера.
Слайд 61Матрицы I (2, 3, 4, 5)
Слайд 62Множество ограничений E(n)
Обозначим множество ограничений, вытекающих из вероятностной аксиоматики, как E(n). В матрично-векторном виде они записываются как
Слайд 63ФЗ с [,]-ми оценками
Задан набор интервальных оценок, который мы обозначим как D(n).
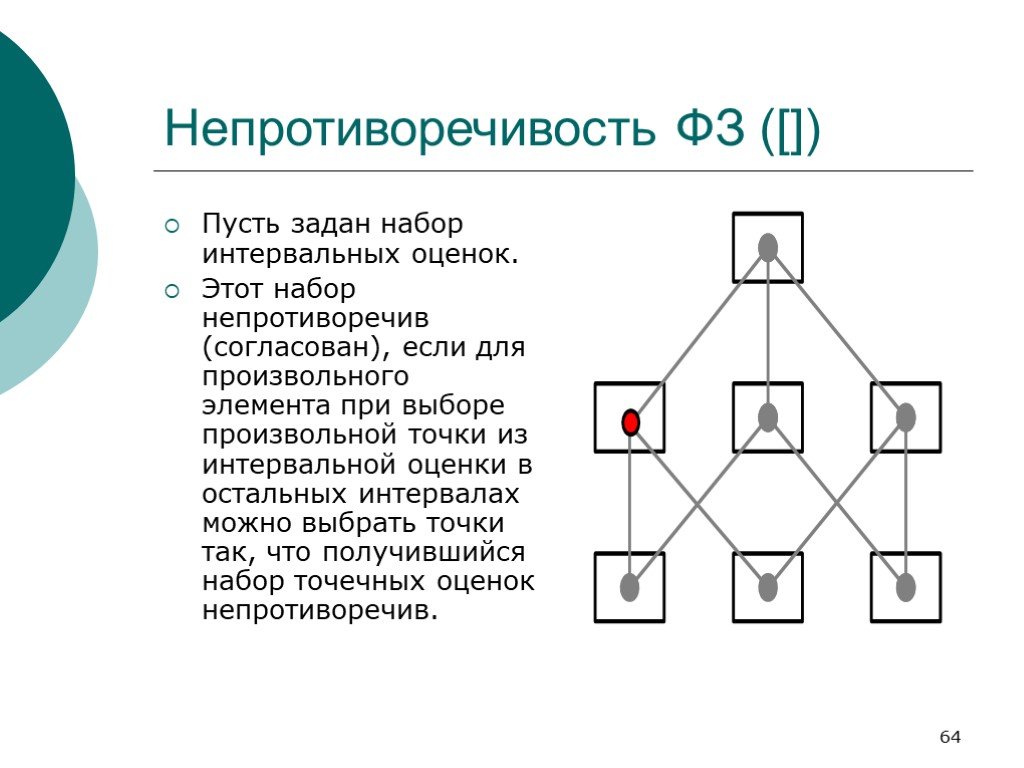
Слайд 64Непротиворечивость ФЗ ([])
Пусть задан набор интервальных оценок. Этот набор непротиворечив (согласован), если для произвольного элемента при выборе произвольной точки из интервальной оценки в остальных интервалах можно выбрать точки так, что получившийся набор точечных оценок непротиворечив.
Слайд 65Поддержание непротиворечивости ФЗ в [,]-ом случае
Слайд 66Априорный вывод
Можно как выводить оценку истинности пропозиции, не вошедшей в ФЗ, так и учитывать эту оценку в процессе поддержания непротиворечивости или априорного вывода оценок вероятности истинности других формул.
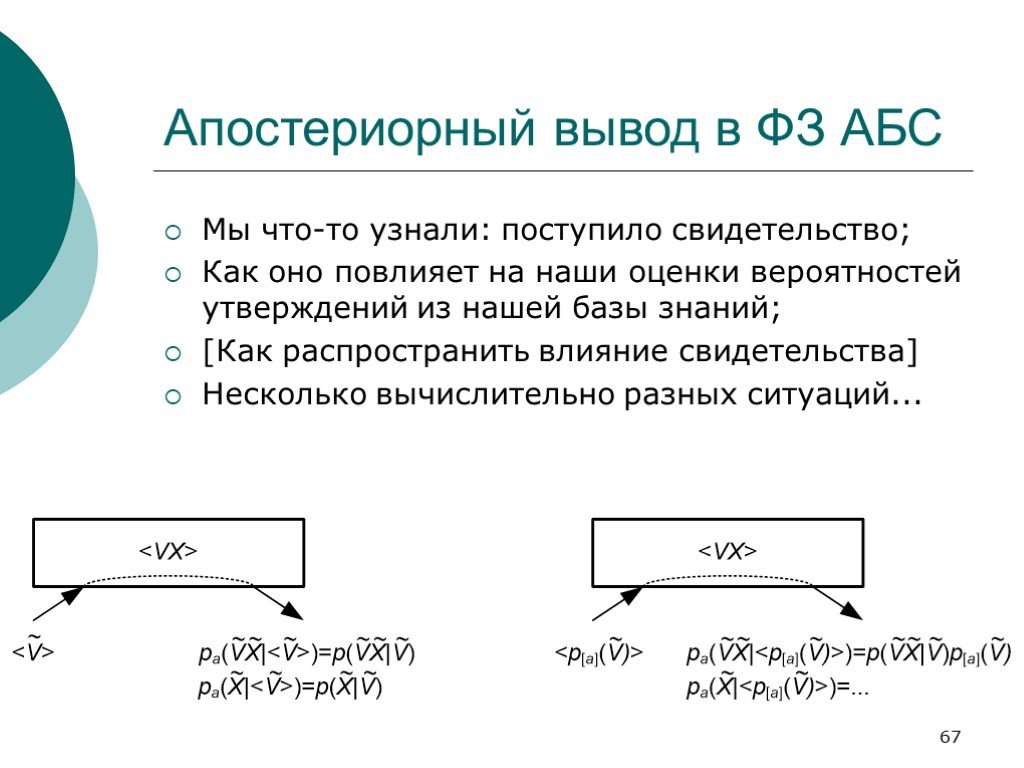
Слайд 67Апостериорный вывод в ФЗ АБС
Мы что-то узнали: поступило свидетельство; Как оно повлияет на наши оценки вероятностей утверждений из нашей базы знаний; [Как распространить влияние свидетельства] Несколько вычислительно разных ситуаций...
Слайд 68Детерминированное свидетельство
Атомарные или и кортежи , , ... Кратко
Слайд 69Недетерминированное свидетельство
Атомарные
и Кортежи В краткой записи:
Апостериорное распределение вероятностей (задающее свидетельство) подчиняется аксиомам вероятностной логики. В нашей теории кортеж недетерминированных свидетельств также представляется в виде фрагмента знаний.
Слайд 70Свидетельство с неопределенностью
Кортеж недетерминированных свидетельств с неопределенностью представляется в виде фрагмента знаний с интервальными оценками истинности.
Слайд 71Апостериорный вывод: (.) и [,]
Вид оценок в ФЗ, куда поступает свидетельство, также создают особый вычислительный аспект: точечные оценки --- «прямые» вычисления по определению условной вероятности; интервальные оценки --- задачи гиперболического программирования.
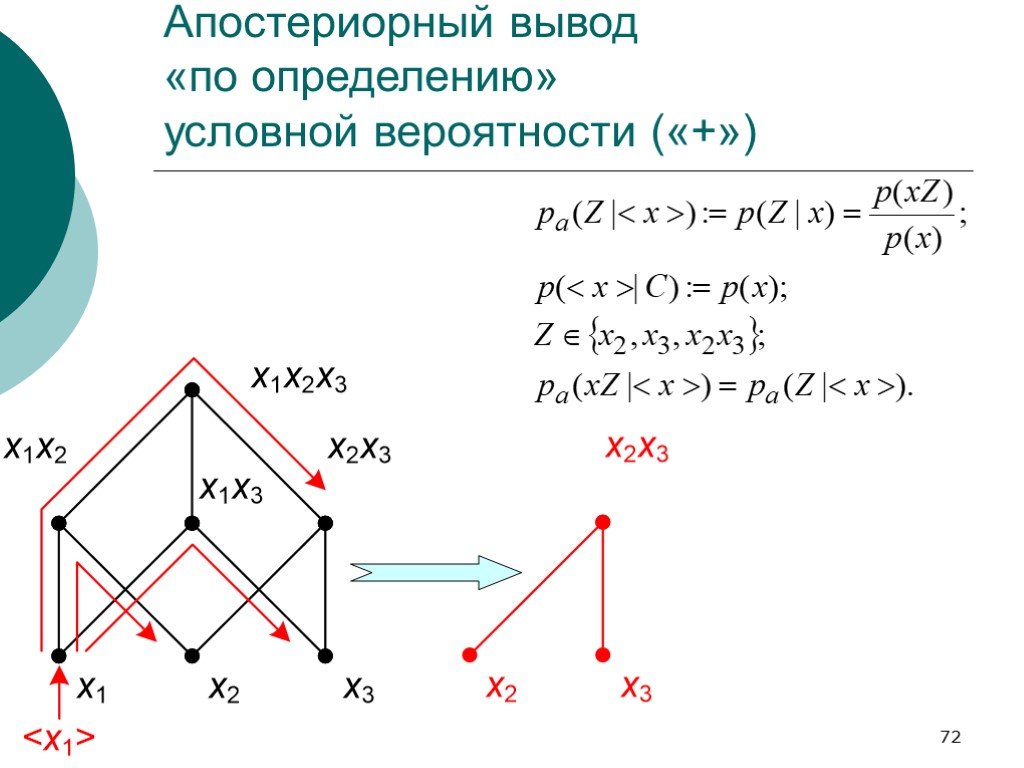
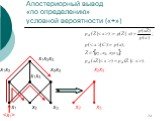
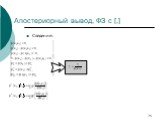
Слайд 72Апостериорный вывод «по определению» условной вероятности («+»)
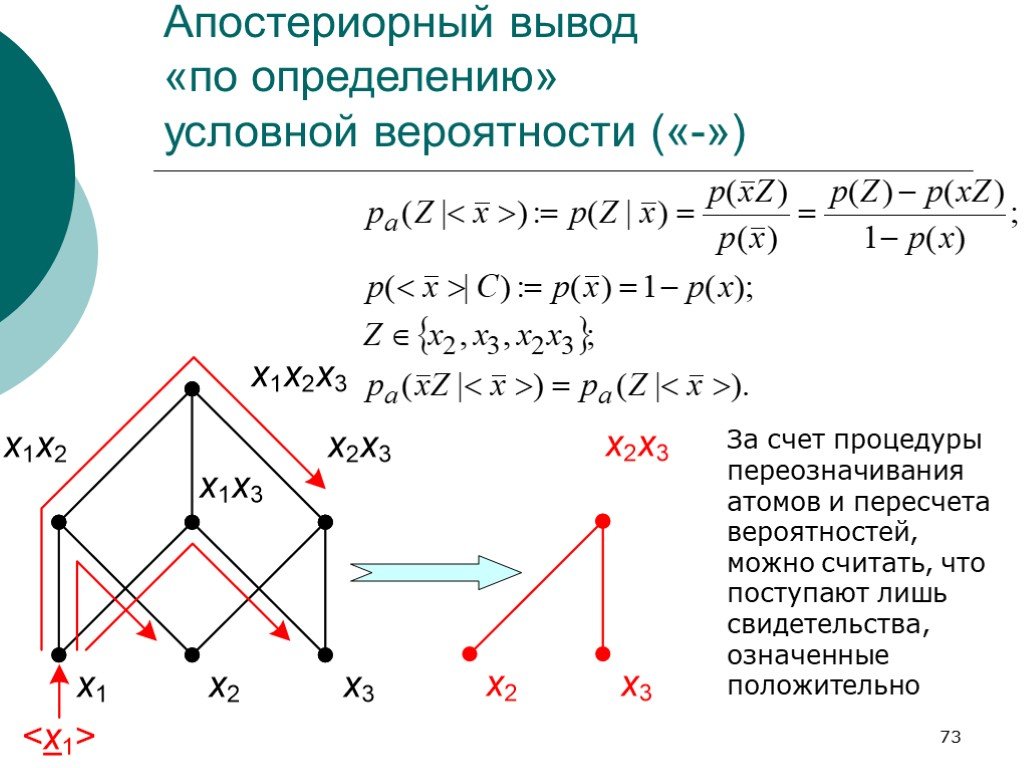
Слайд 73Апостериорный вывод «по определению» условной вероятности («-»)
За счет процедуры переозначивания атомов и пересчета вероятностей, можно считать, что поступают лишь свидетельства, означенные положительно
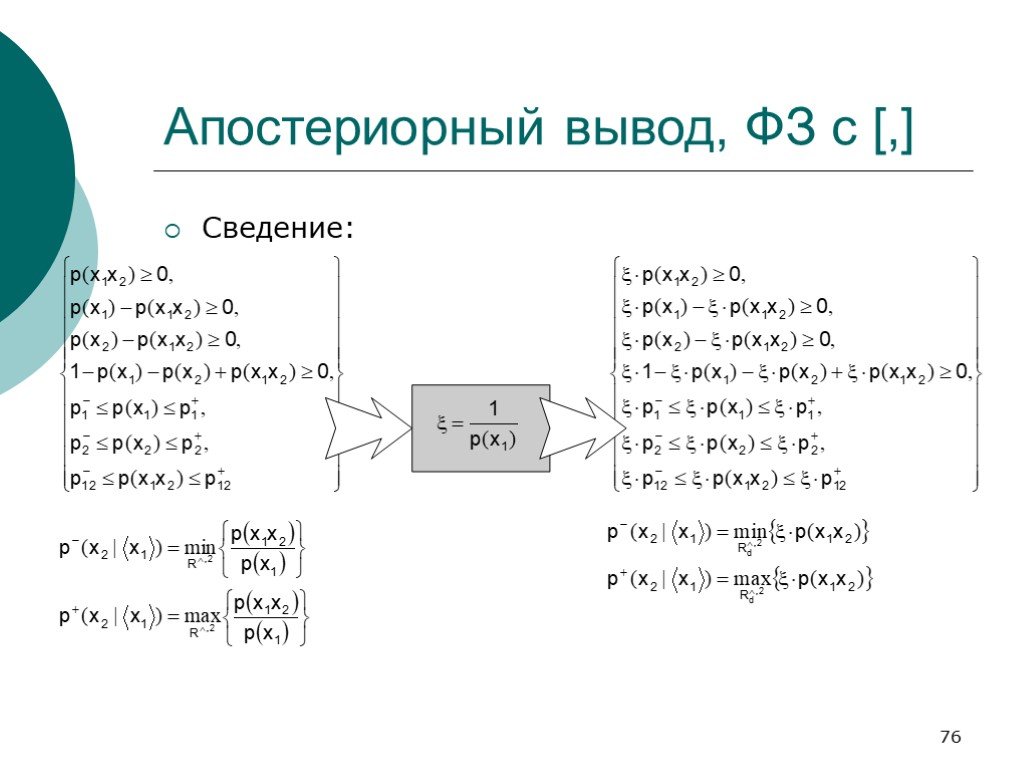
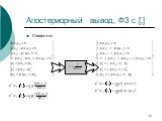
Слайд 74Апостериорный вывод, ФЗ с [,]
Сведение:
Слайд 75
Слайд 76
Слайд 77
Слайд 78
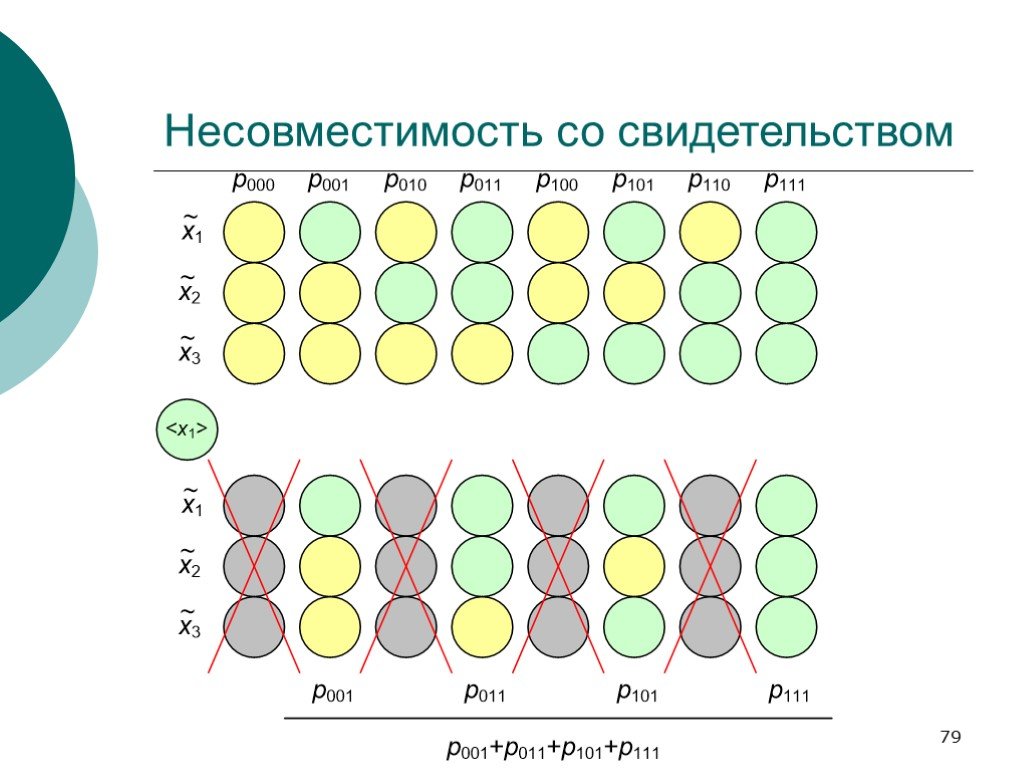
Слайд 79Несовместимость со свидетельством
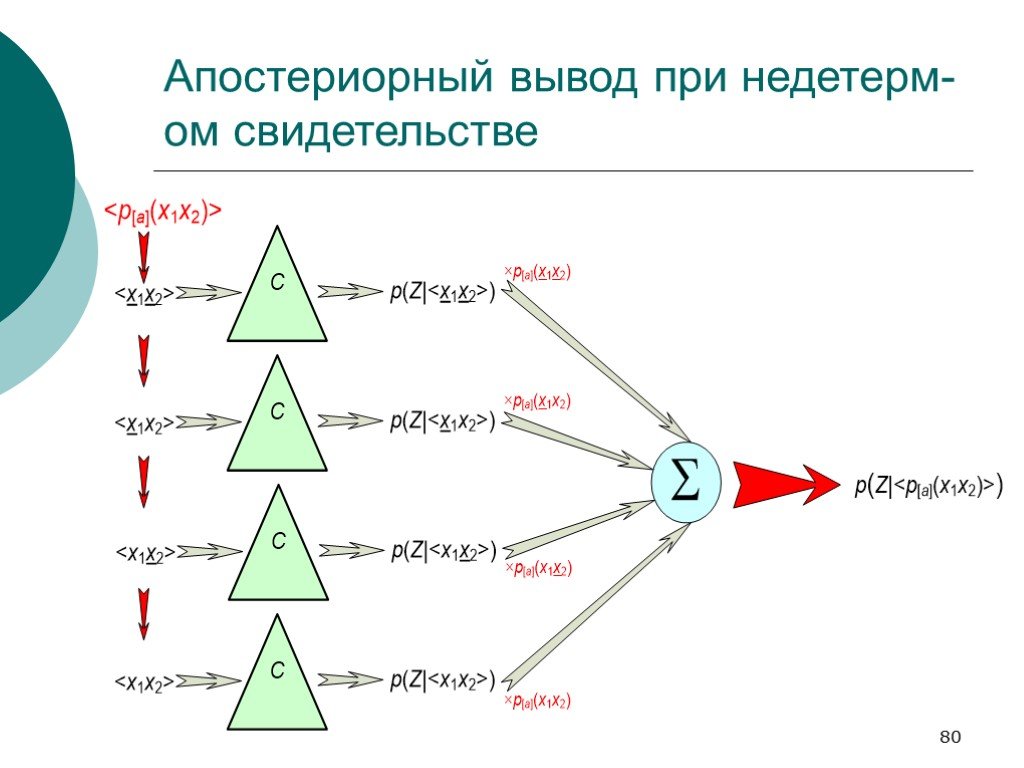
Слайд 80Апостериорный вывод при недетерм-ом свидетельстве
Слайд 81Примеры формул для рассчетов
Слайд 82
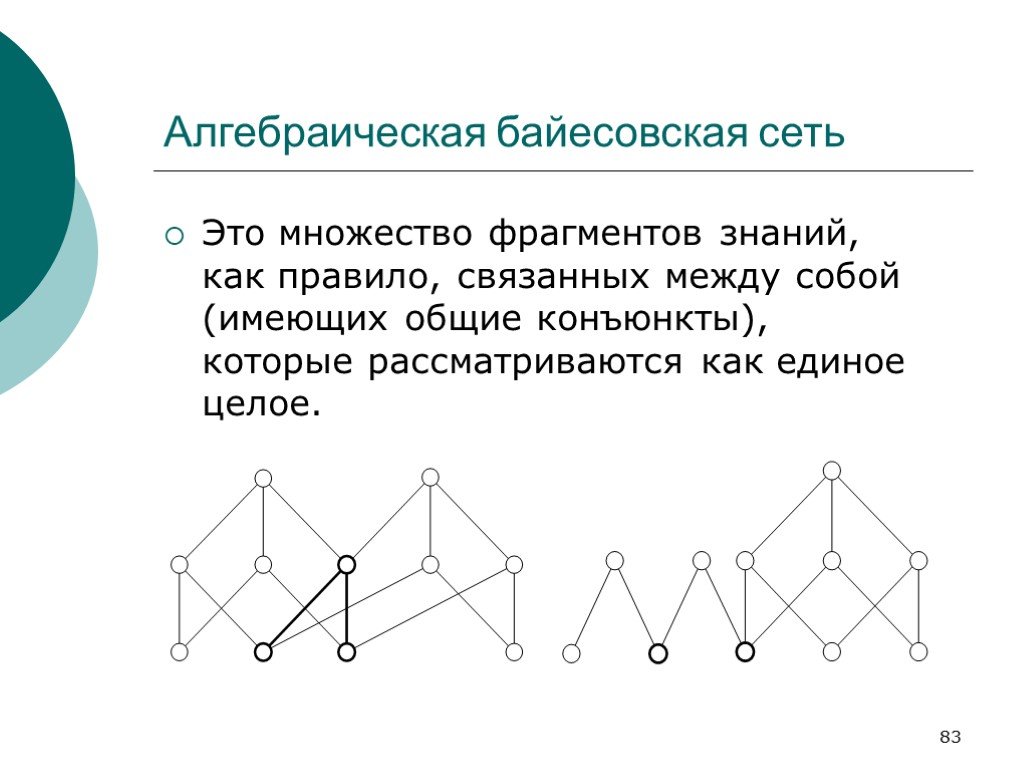
Слайд 83Алгебраическая байесовская сеть
Это множество фрагментов знаний, как правило, связанных между собой (имеющих общие конъюнкты), которые рассматриваются как единое целое.
Слайд 84Граф и дерево смежности - веса
Узлу графа смежности ставится в соответствие фрагмент знаний; весом же узла является идеал конъюнктов, лежащий в основе этого ФЗ.
Слайд 85Граф смежности --- определение
Графом смежности называется ненаправленный граф, в котором между каждой парой узлов, веса которых содержат общие элементы, существует путь; в веса каждого из узлов любого пути (в графе) входят все элементы, общие для начального и конечного узлов этого пути; вес одного узла не входит полностью в вес никакого другого узла.
Слайд 86Сепараторы
Каждому ребру в графе смежности также удобно приписать вес – пересечение весов, приписанных тем двум узлам, которые соединяются рассматриваемым ребром. Вес на ребре --- сепаратор (или разделитель). Непустое пересечение идеалов конъюнктов --- идеал конъюнктов.
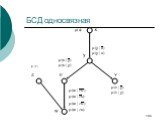
Слайд 87Дерево смежности
Деревом смежности называется ациклический граф смежности --– такой граф, что в нем нет ни одного цикла, то есть пути (без повторяющихся узлов), начало и конец которого бы совпали.
Слайд 88АБС --- определение
Алгебраическая байесовская сеть (АБС) определяется как граф смежности с фрагментами знаний в узлах. АБС, представимая в виде дерева смежности, называется ациклической (ААБС). АБС является одной из логико-вероятностных моделей БФЗ с неопределенностью.
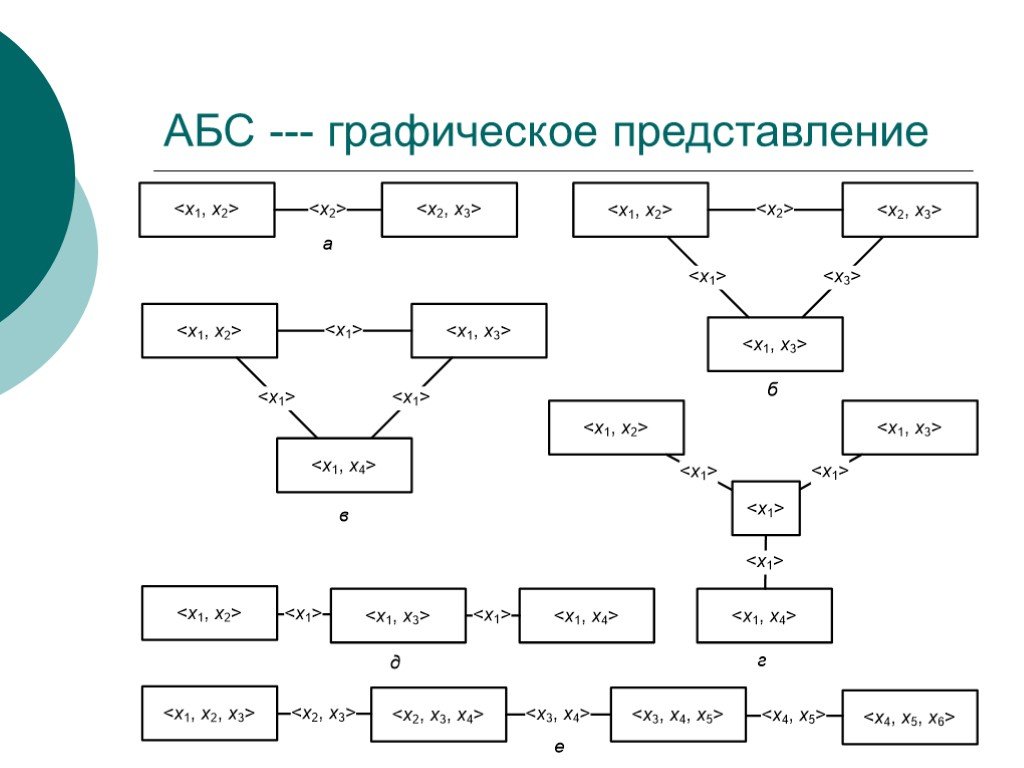
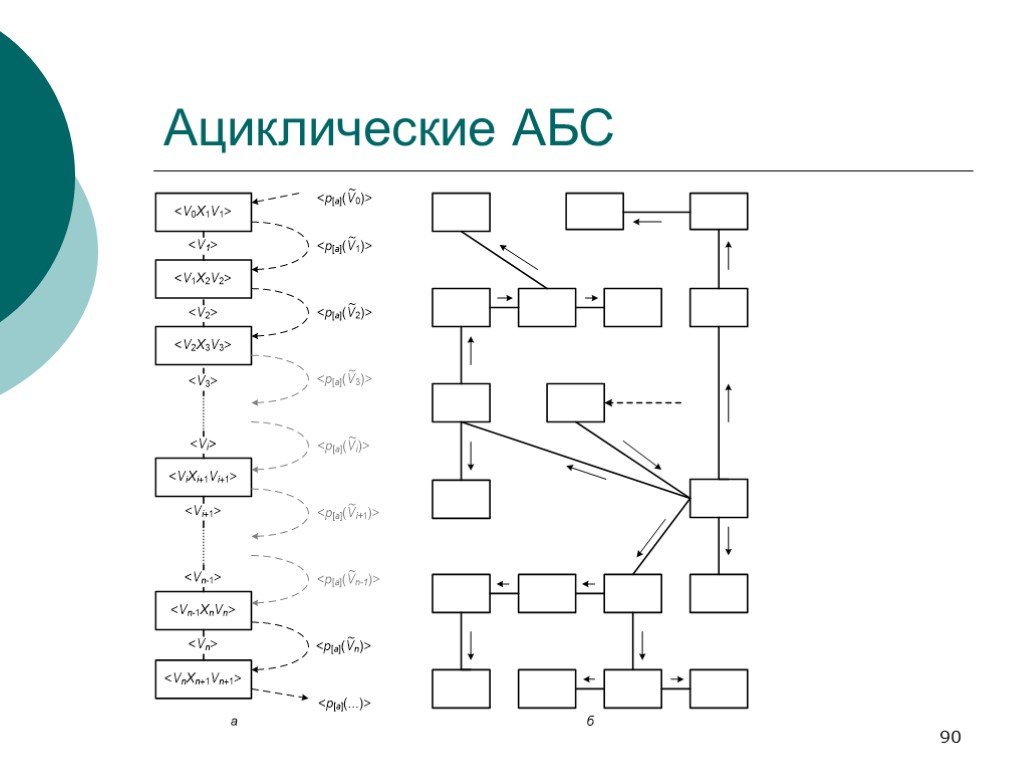
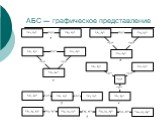
Слайд 89АБС --- графическое представление
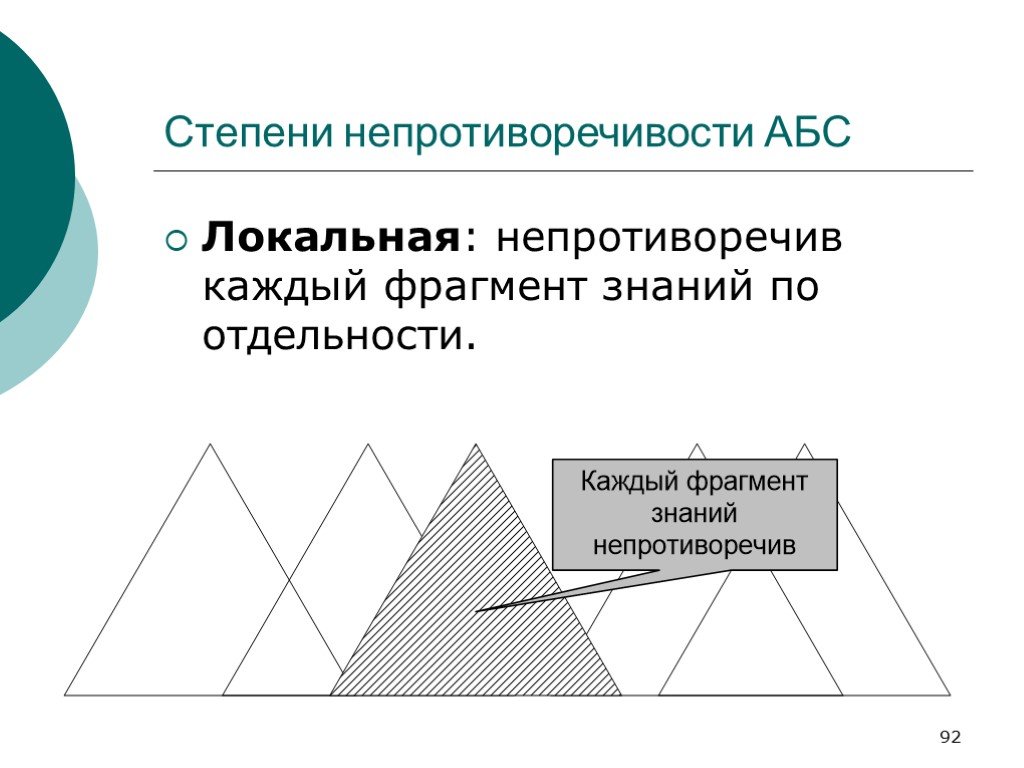
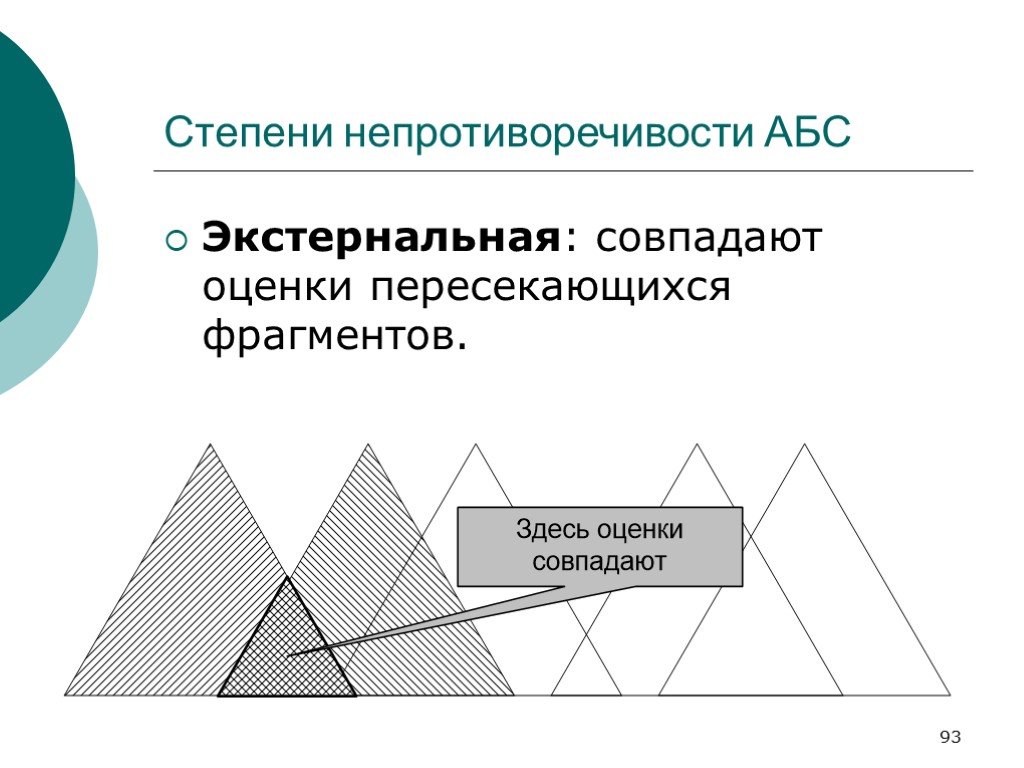
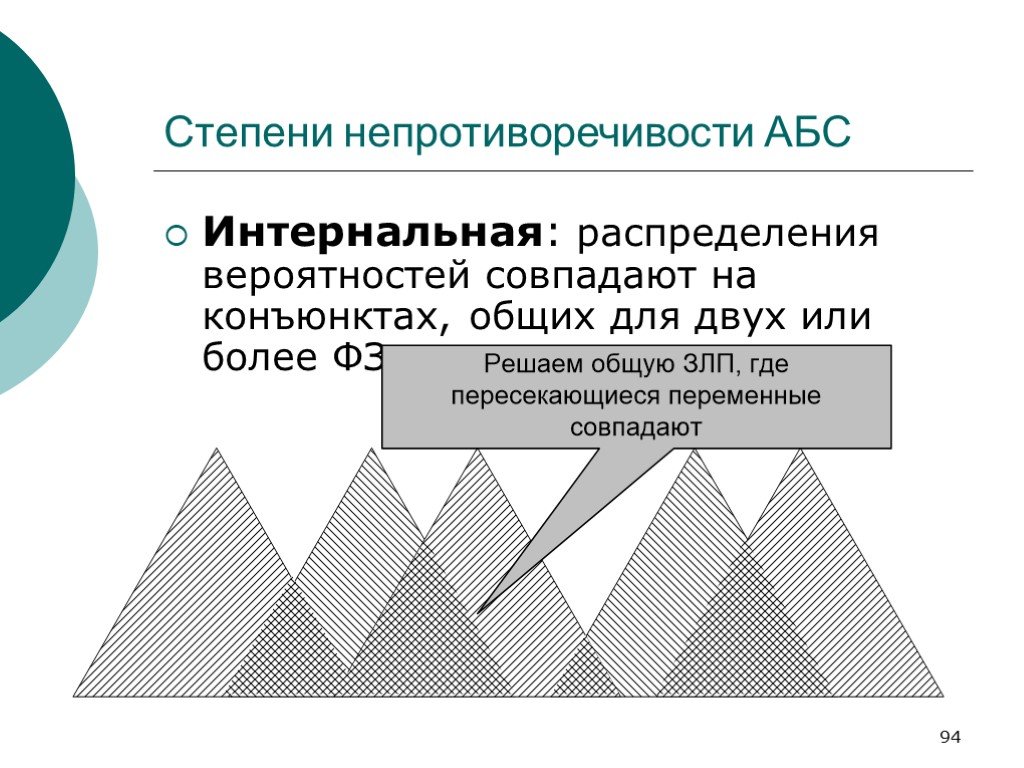
Слайд 91Степени непротиворечивости АБС
Локальная, Экстернальная, Интернальная, Глобальная
Слайд 92Локальная: непротиворечив каждый фрагмент знаний по отдельности.
Слайд 93Экстернальная: совпадают оценки пересекающихся фрагментов.
Слайд 94Интернальная: распределения вероятностей совпадают на конъюнктах, общих для двух или более ФЗ.
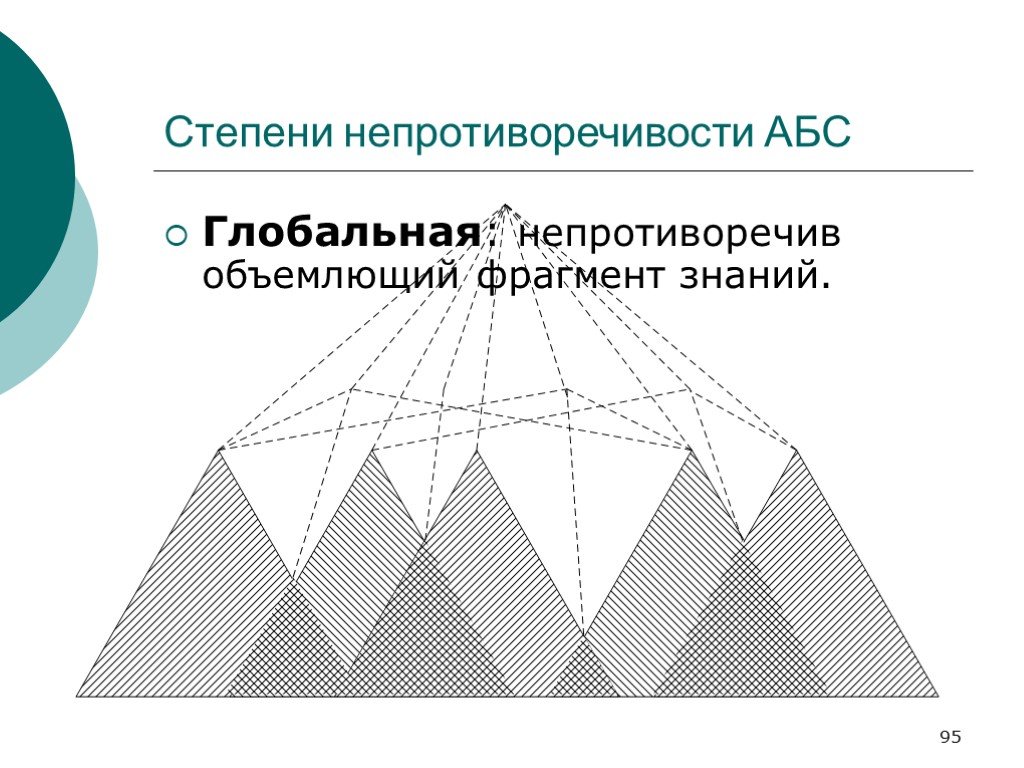
Слайд 95Глобальная: непротиворечив объемлющий фрагмент знаний.
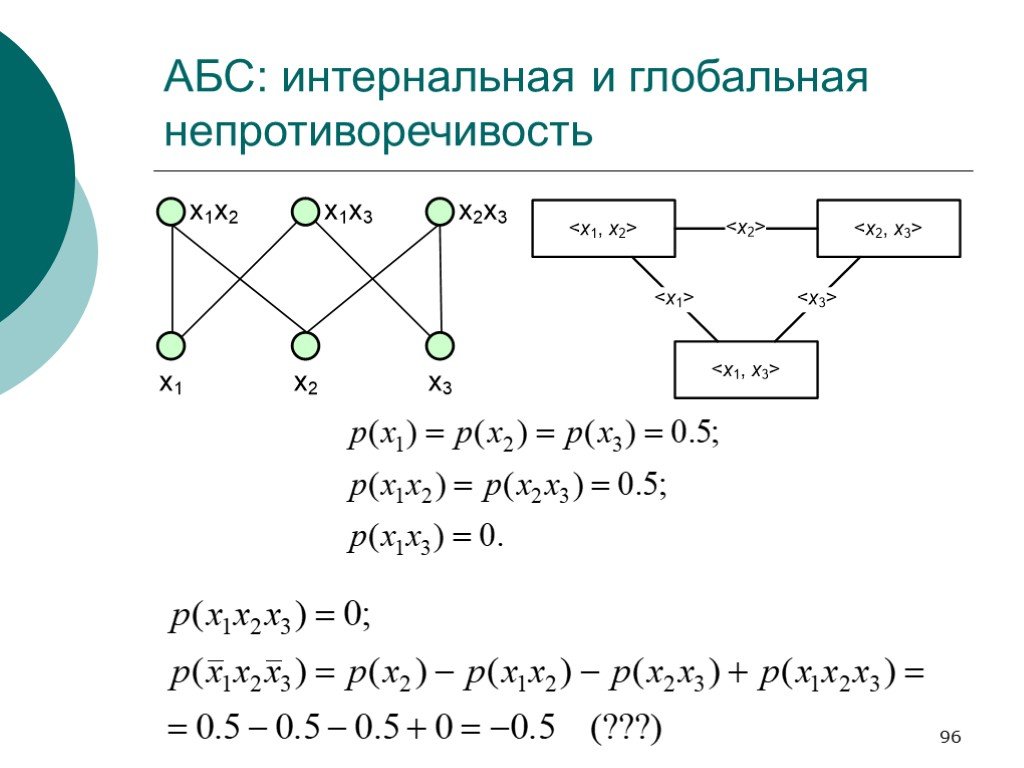
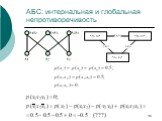
Слайд 96АБС: интернальная и глобальная непротиворечивость
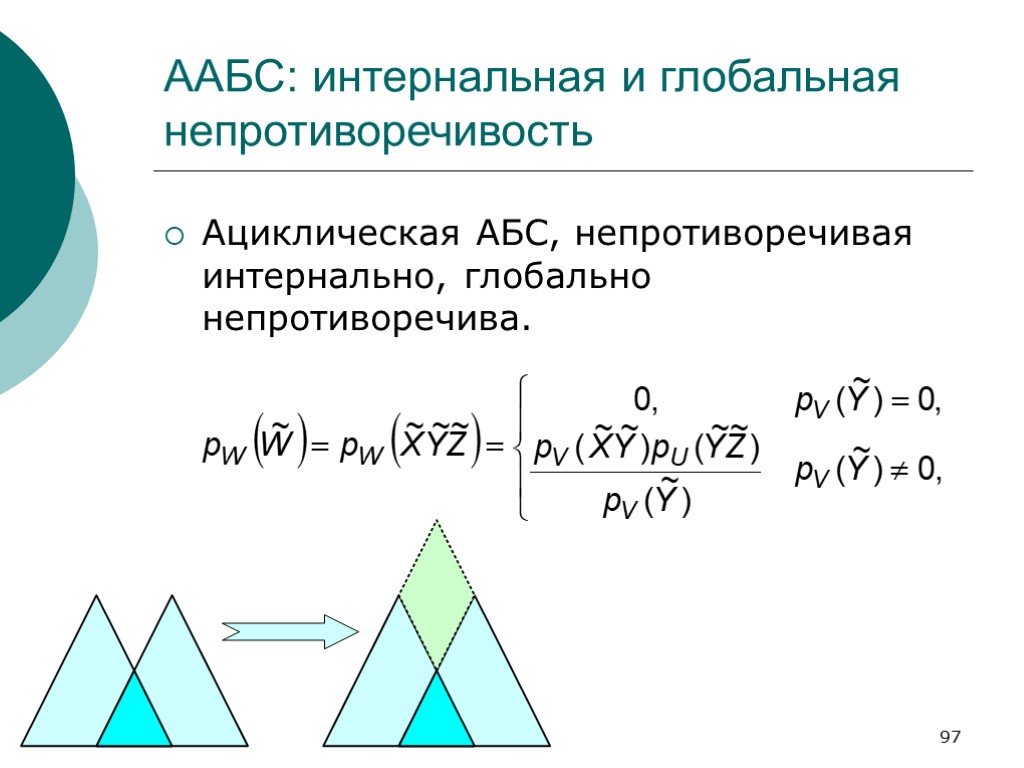
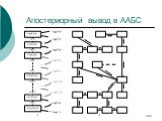
Слайд 97ААБС: интернальная и глобальная непротиворечивость
Ациклическая АБС, непротиворечивая интернально, глобально непротиворечива.
Слайд 98ААБС: интернальная и экстернальная непротиворечивость
Экстернально непротиворечивая ациклическая АБС может быть интернально противоречивой. Есть класс ациклических сетей, у которых из экстернальной непротиворечивости следует интернальная.
Слайд 99Апостериорный вывод: свидетельства
Детерминированное свидетельство (и кортеж ДС); Недетерминированное свидетельство (и кортеж НДС); Недетерминированное свидетельство (и кортеж НДСН).
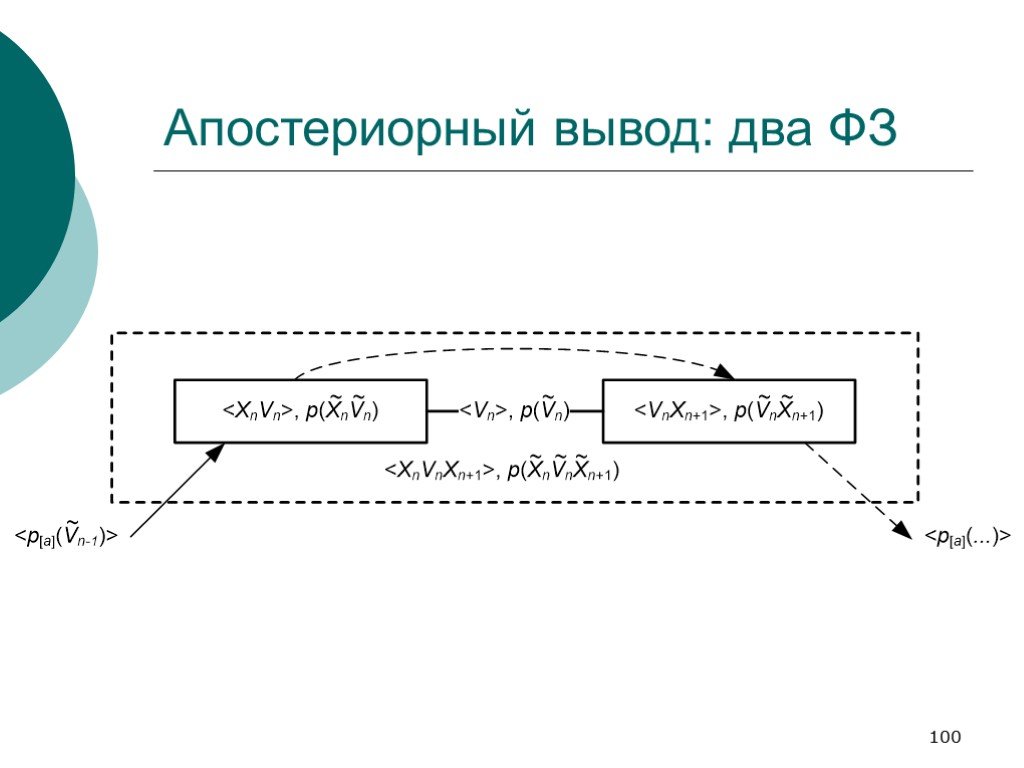
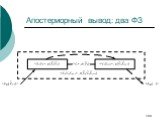
Слайд 100Апостериорный вывод: два ФЗ
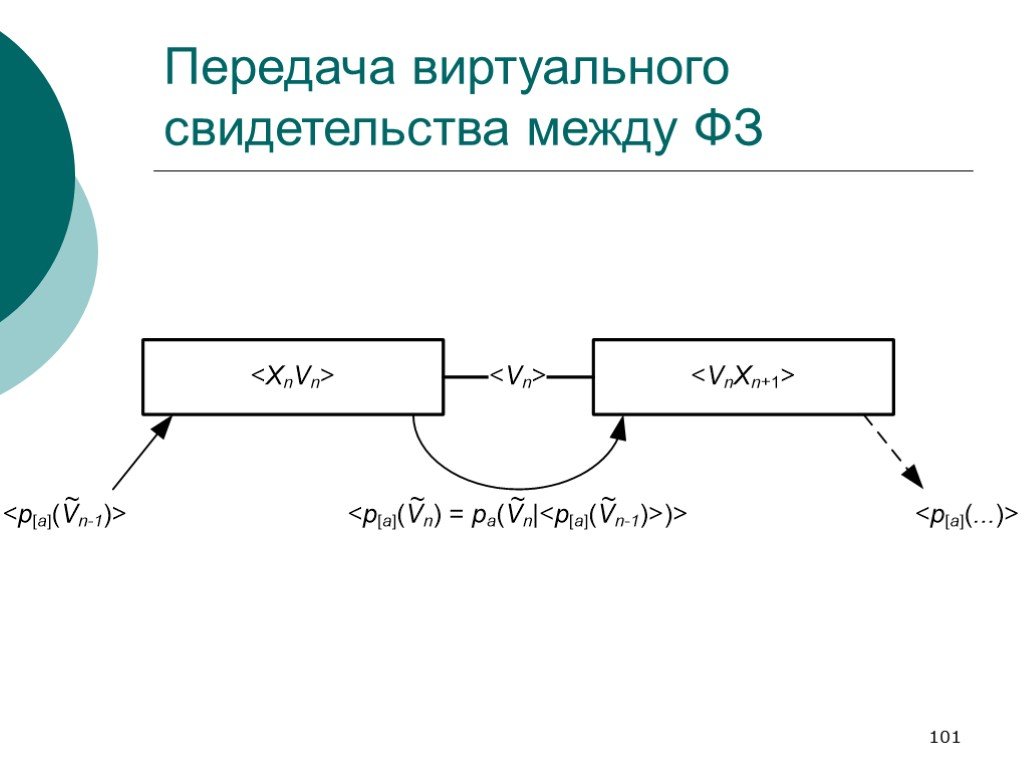
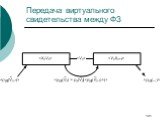
Слайд 101Передача виртуального свидетельства между ФЗ
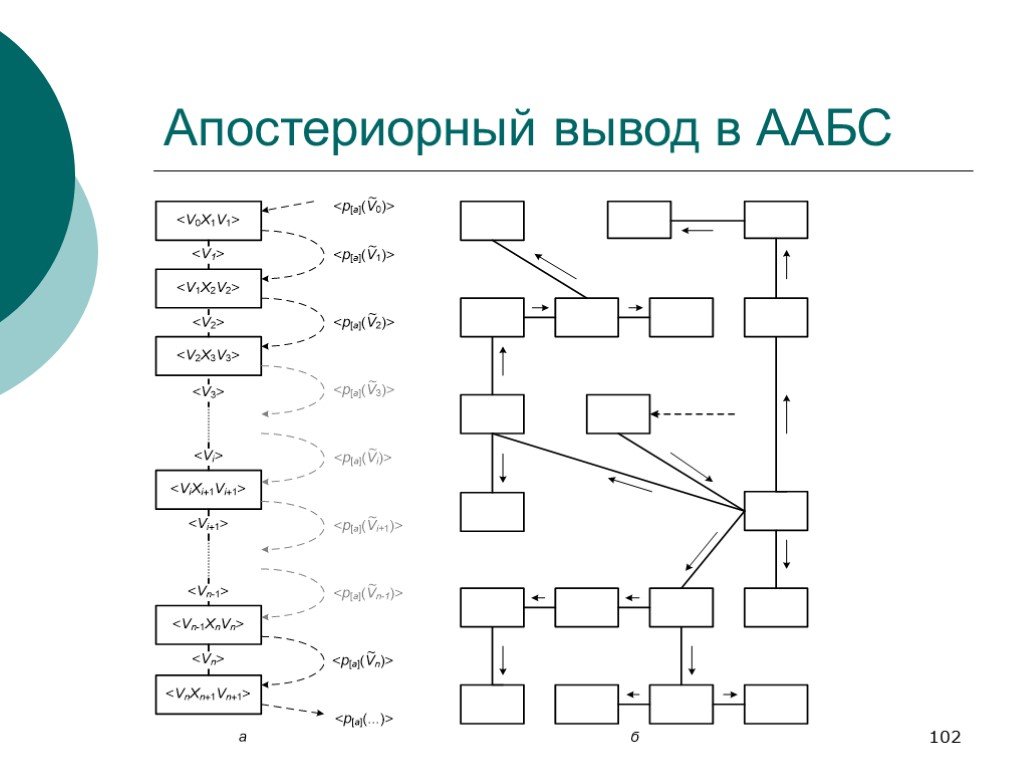
Слайд 102Апостериорный вывод в ААБС
Слайд 103
Слайд 104Основная цель байесовских сетей доверия, как и в случае АБС,— представление распределения вероятностей над переменными (возможно многозначными) в удобном для обработки и компактном виде.
В качестве такого представления выбран ациклический направленный граф с тензорами условных вероятностей.
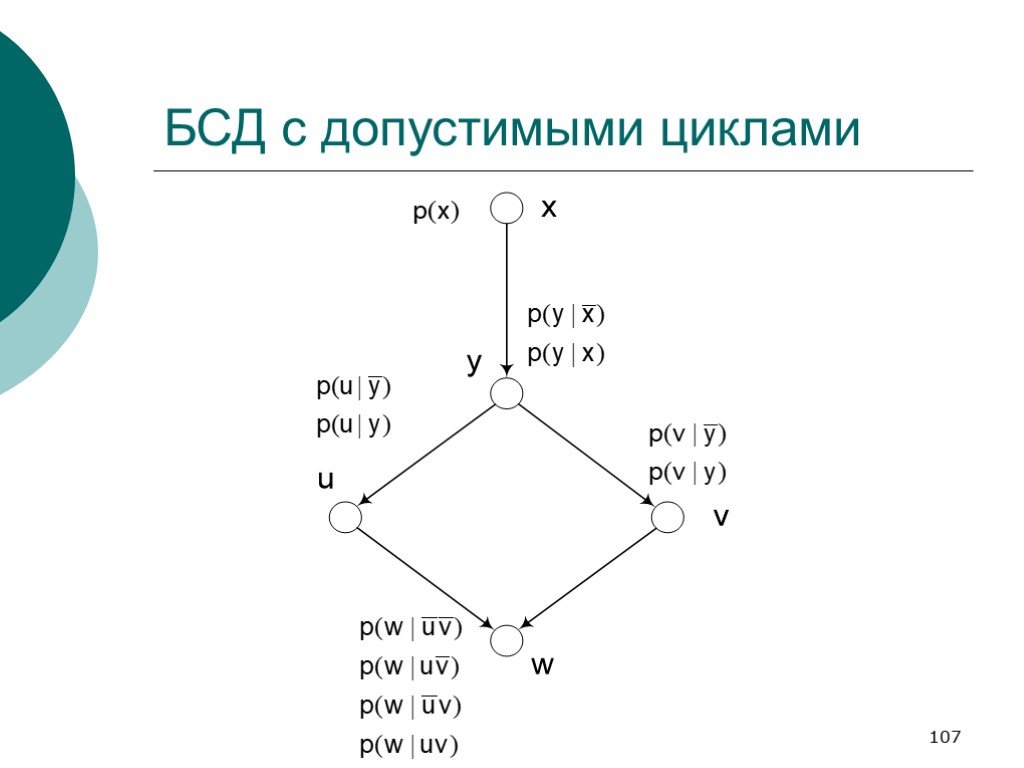
Слайд 107БСД с допустимыми циклами
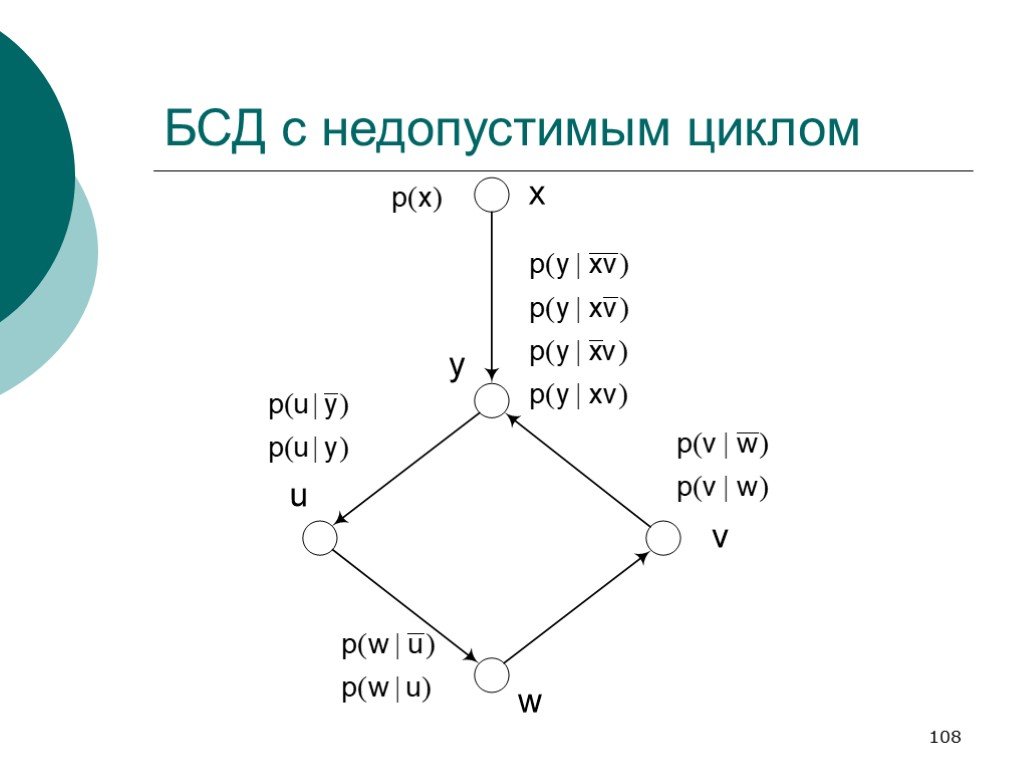
Слайд 108БСД с недопустимым циклом
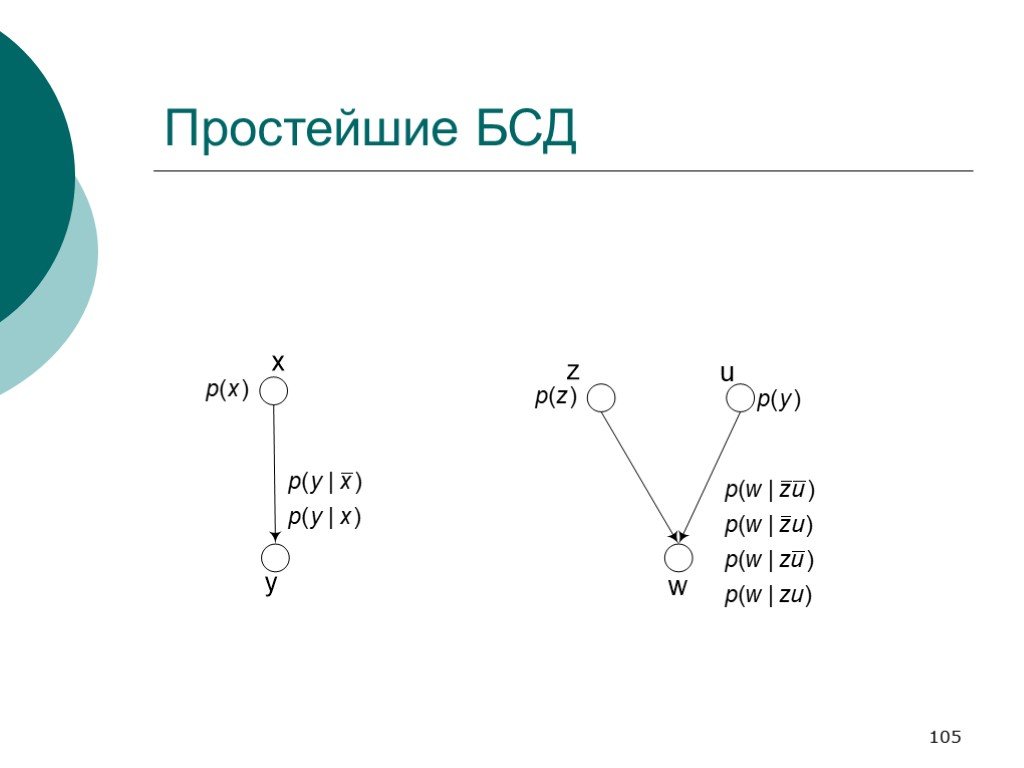
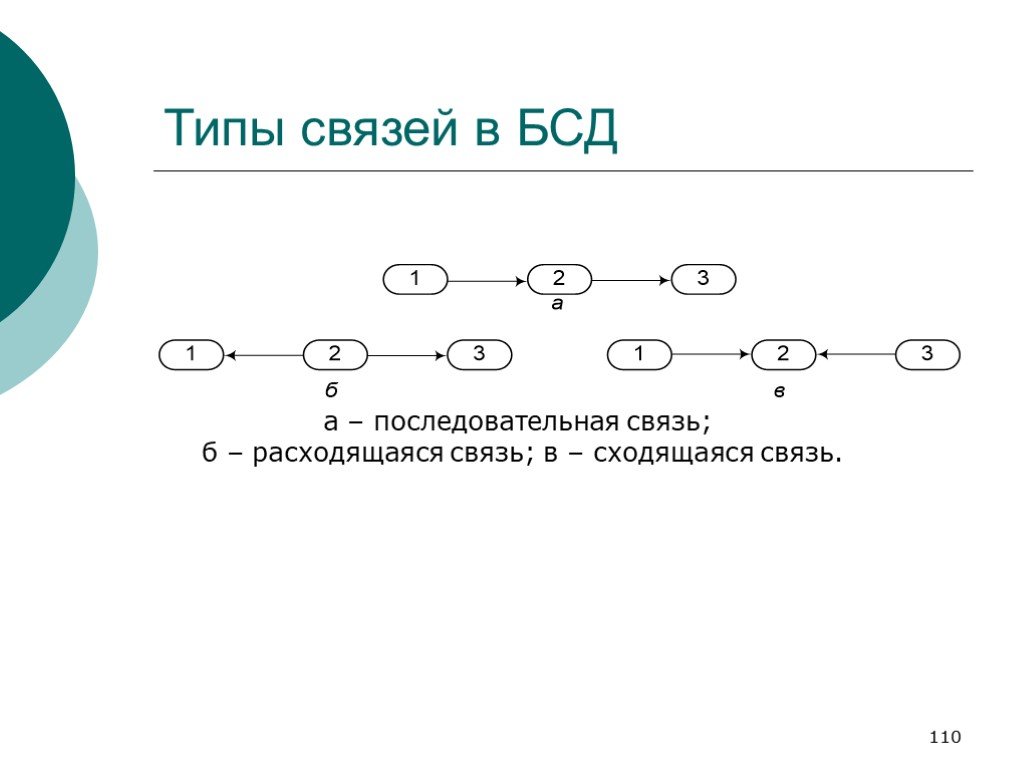
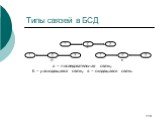
Слайд 110Типы связей в БСД
а – последовательная связь; б – расходящаяся связь; в – сходящаяся связь.
Слайд 111Понятие d-разделимости
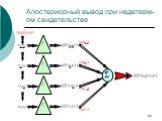
Два узла называются d-разделимыми, если любой путь между ними содержит последовательную или сходящуюся связь, в центральный узел которой поступило свидетельство, или расходящуюся связь, в центральный узел (и его потомки) которой не поступило свидетельство.
Слайд 112Основное предположение
d-разделенные узлы независимы. Это предположение позволяет однозначно восстановить распределение вероятностей над всеми переменными.
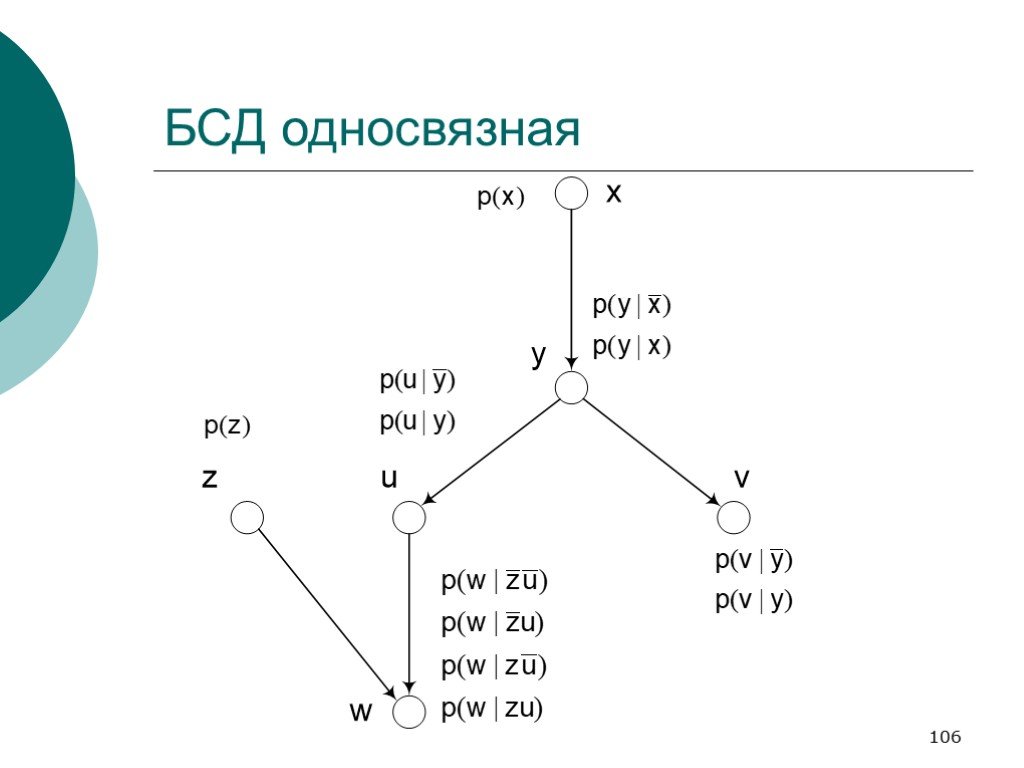
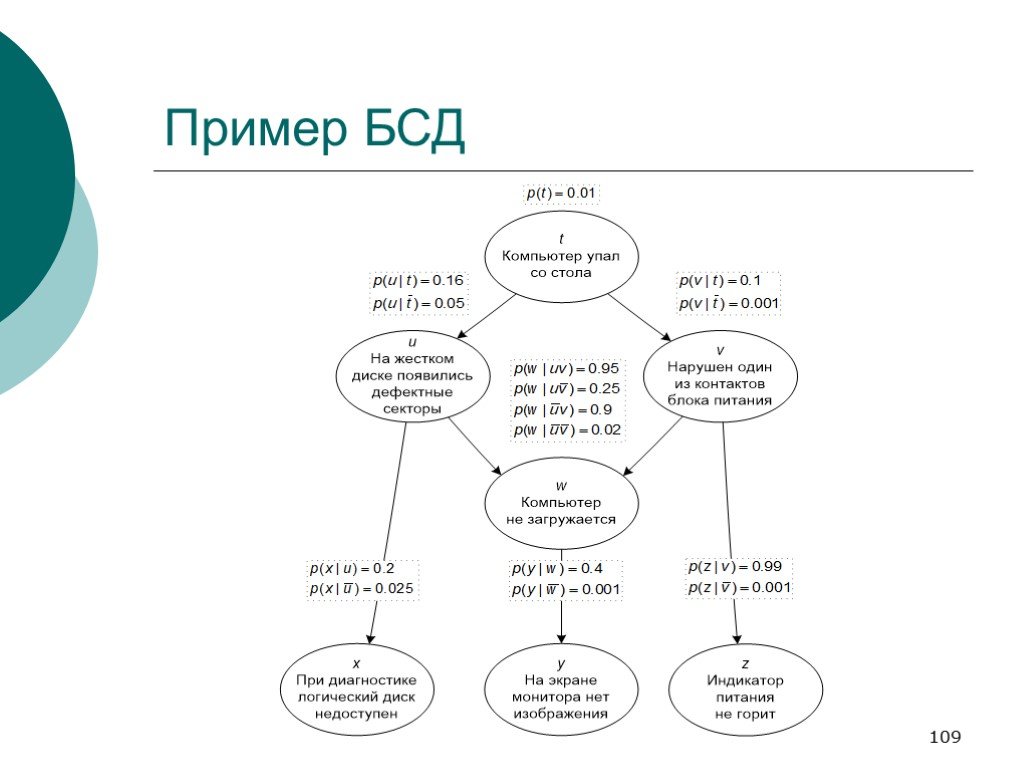
Слайд 113Несколько условий формально на примере нашей сети
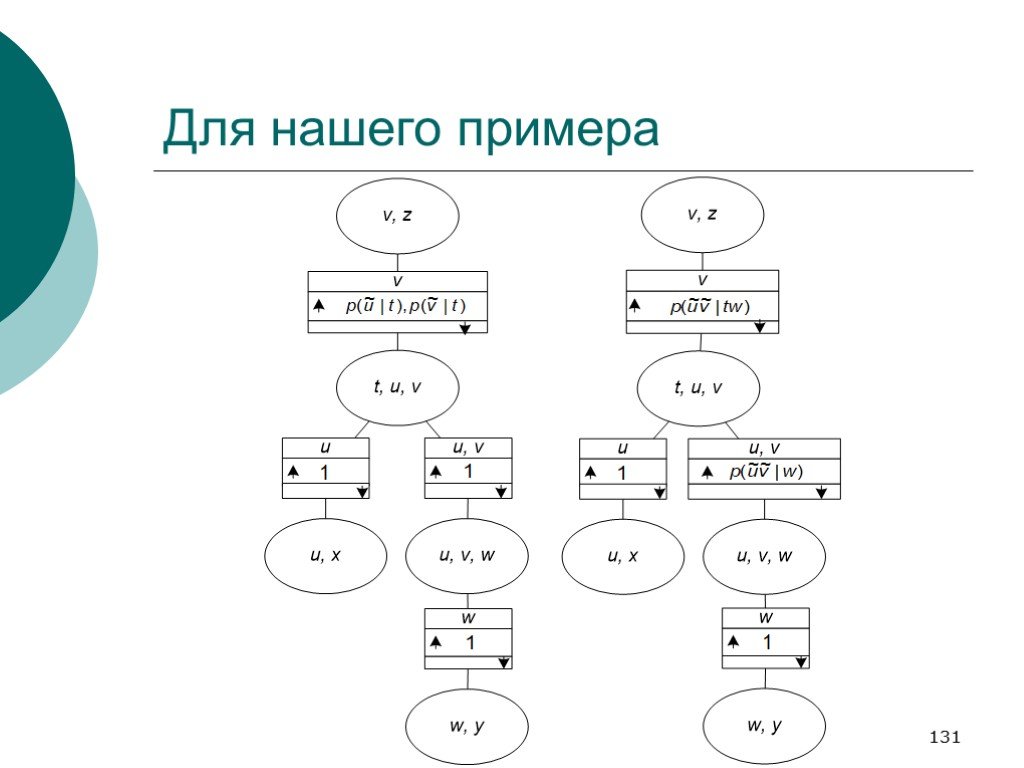
p(u|t) × p(v|t) = p(uv|t) p(t|uv) × p(w|uv) = p(tw|uv) … В такой форме эти предположения уже не кажутся столь очевидными
Слайд 114Что нам дают такие предположения
Независимость d-разделимых [переменных в узлах] позволяет выделить единственное распределение из всех, для которых подходят заданные условные вероятности. Это единственное распределение -- произведение всех вероятностей, заданных в БСД (chain rule).
Слайд 115Chain rule для нашего примера
Слайд 116Но все же…
Несмотря на указанную выше формализацию, методы работы с БСД позволяют использовать chain rule неявно.
Слайд 117Первичная пропагация
Вычисление вероятностей всех переменных (по отдельности), входящих в нашу сеть.
Слайд 118Простейший (в лоб) алгоритм первичной пропагации
По определению условной вероятности: Аналогично хочется поступить с остальными вероятностями.
Слайд 119Алгоритм первичной пропагации для ациклических направленных графов
Очевидно, что в описанном выше примере нам в ходе вычисления p(w) потребуются вероятности именно в такой ситуации и требуется chain rule и понятие d-разделимости. В частности получаем, что p(uv|t) = p(u|t) × p(v|t), аналогично для отрицания t и суммируем.
Слайд 120Первичная пропагация, обобщенный алгоритм «на пальцах»
Если мы хотим вычислить вероятность какого либо узла, то мы должны просуммировать совместное распределение по означиванию всех остальных переменных (маргинализовать). Но, так как все наше распределение разбивается на произведение достаточно простых, можно проводить суммирование по очереди по одной (иногда по нескольким) переменным за раз, при этом большая часть сомножителей не будет от них зависеть.
Слайд 121Первичная пропагация связь простого и обобщенного алгоритмов
Простой алгоритм — это всего лишь удачный порядок суммирования для обобщенного алгоритма. Обобщенный алгоритм понадобится при появлении свидетельств. Для обобщенного алгоритма удобно определить на БСД структуру дерева смежности.
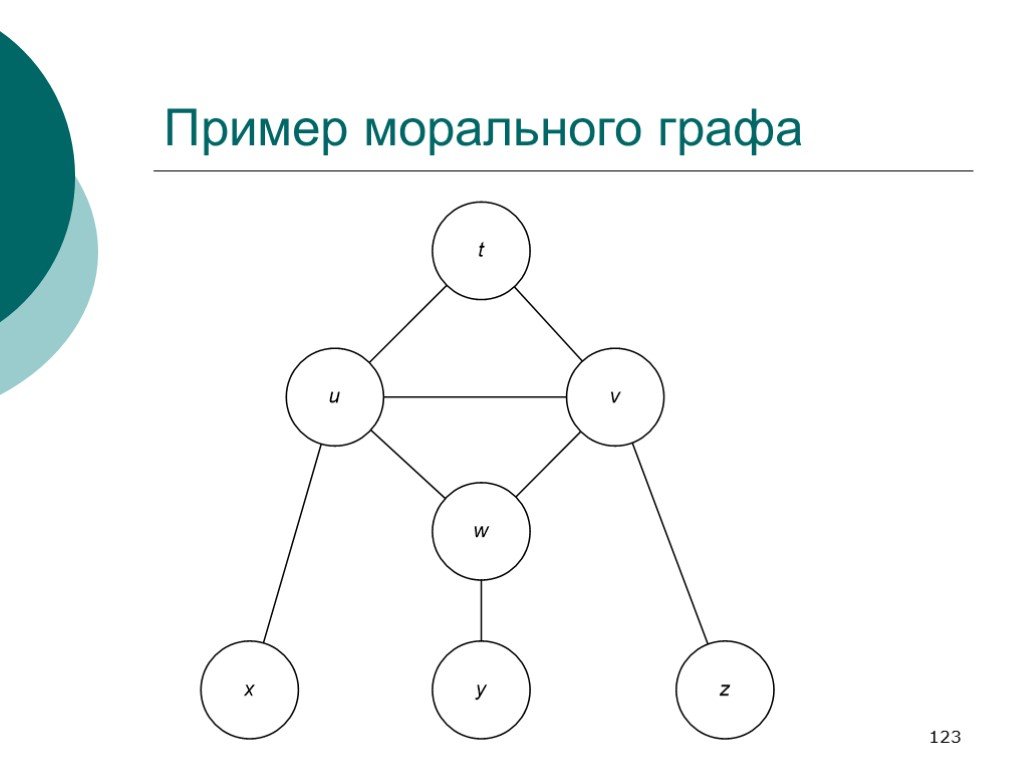
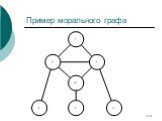
Слайд 122Моральный граф
Моральным графом для БСД называется ненаправленный граф, в котором вершины те же, и две вершины соединены ребром, если они либо соседствуют, либо имеют общего сына в исходной БСД.
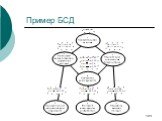
Слайд 123Пример морального графа
Слайд 124Если моральный граф триангулярен
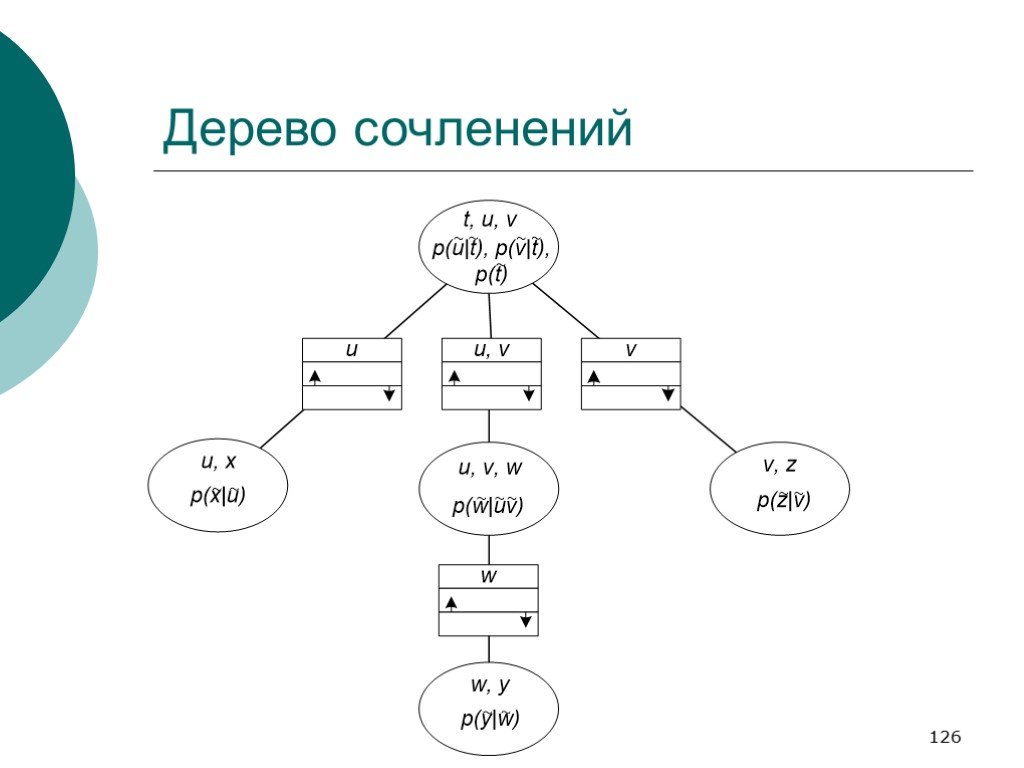
То его можно разбить на клики, которые затем можно объединить в дерево смежностей (разными вариантами). Каждая максимальная клика попадает в отдельный [соответствующий ей] узел дерева смежности.
Слайд 125Если не триангулярен
То придется его триангулировать. Это требуется сделать, добавив, по возможности, «минимум» ребер.
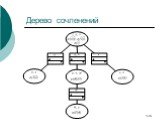
Слайд 126Дерево сочленений
Слайд 127Пропагация свидетельств
Но главная задача БСД — это все-таки пропагация свидетельств (апостериорный вывод). Иными словами, мы знаем апостериорные означивания нескольких узлов и хотим получить условную вероятность остальных.
Слайд 128Переход к пропагации свидетельств
Мы умеем вычислять маргинальные вероятности. Давайте в процессе вычисления в нужном месте «заменим» «настоящую» вероятность единицей или нулем в зависимости от свидетельства. Это гарантирует, что мы получим правильные вероятности в тех узлах, что ниже. Как же учесть влияние на предшествующие узлы?
Слайд 129Алгоритм пропагации свидетельств, «на пальцах»
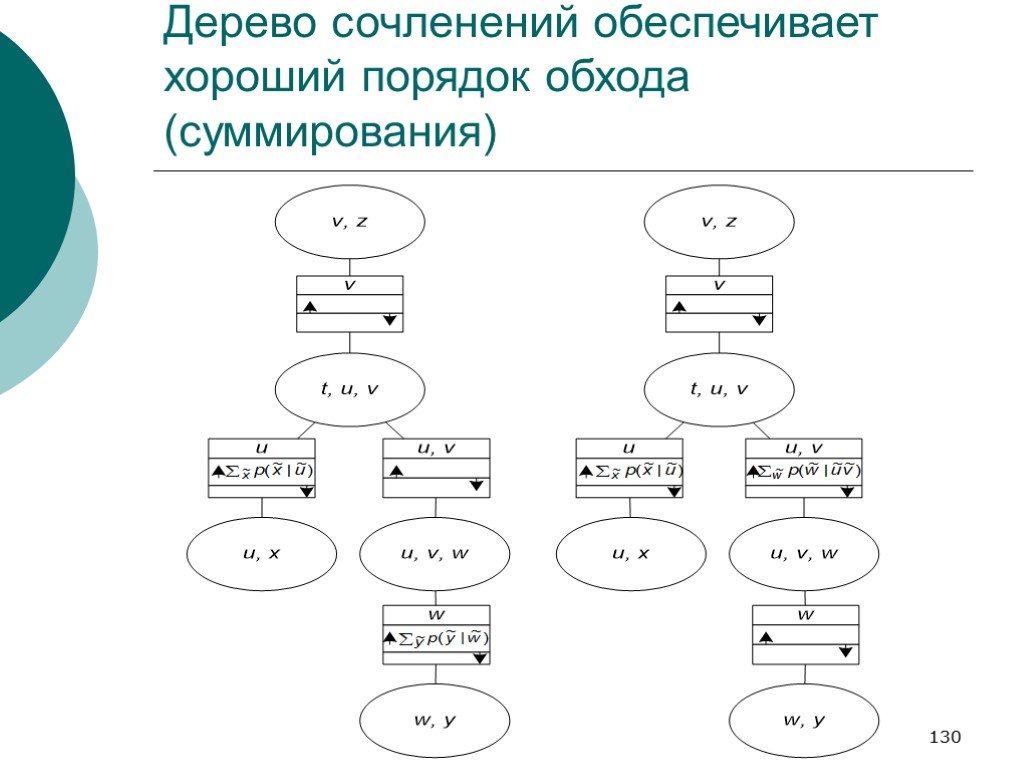
Мы поступим как в обобщенном алгоритме первичной пропагации Для переменной, условную вероятность которой мы хотим получить, нам придется придумать хороший порядок маргинализации из совместного распределения.
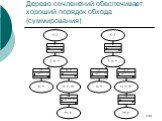
Слайд 130Дерево сочленений обеспечивает хороший порядок обхода (суммирования)
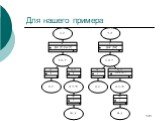
Слайд 131Для нашего примера
Слайд 132Выгода считать все сразу
Двукратный проход по дереву смежности дает нам все искомые вероятности. Для вычисления одной вероятности можно пройти один раз (искомая помещается в вершину).
Слайд 133Проблема направленного цикла
Наличие направленного цикла в байесовской сети доверия приводит к тому, что chain rule не работает. Но часто можно построить распределение, удовлетворяющее заданным условным вероятностям. Такое распределение может быть не единственным: исходным данным может отвечать семейство распределений.
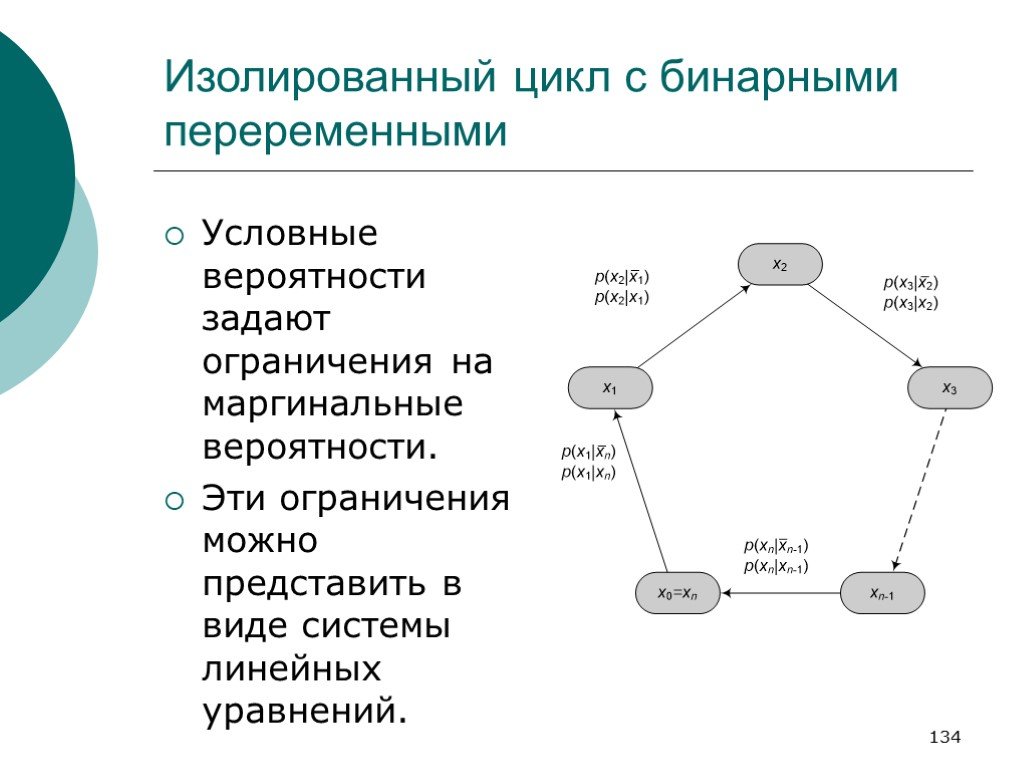
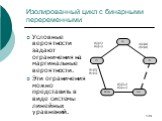
Слайд 134Изолированный цикл с бинарными переременными
Условные вероятности задают ограничения на маргинальные вероятности. Эти ограничения можно представить в виде системы линейных уравнений.
Слайд 135Линейные уравнения, задаваемые изолированным циклом
Слайд 136Линейные уравнения, задаваемые изолированным циклом, в матричном представлении
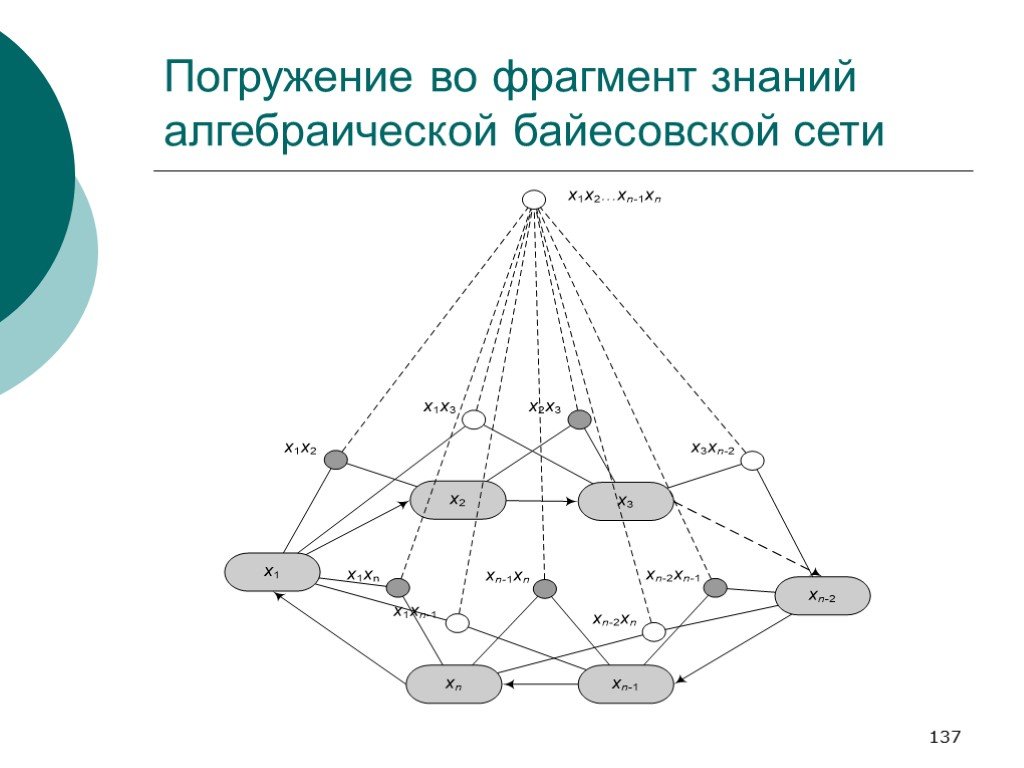
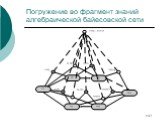
Слайд 137Погружение во фрагмент знаний алгебраической байесовской сети
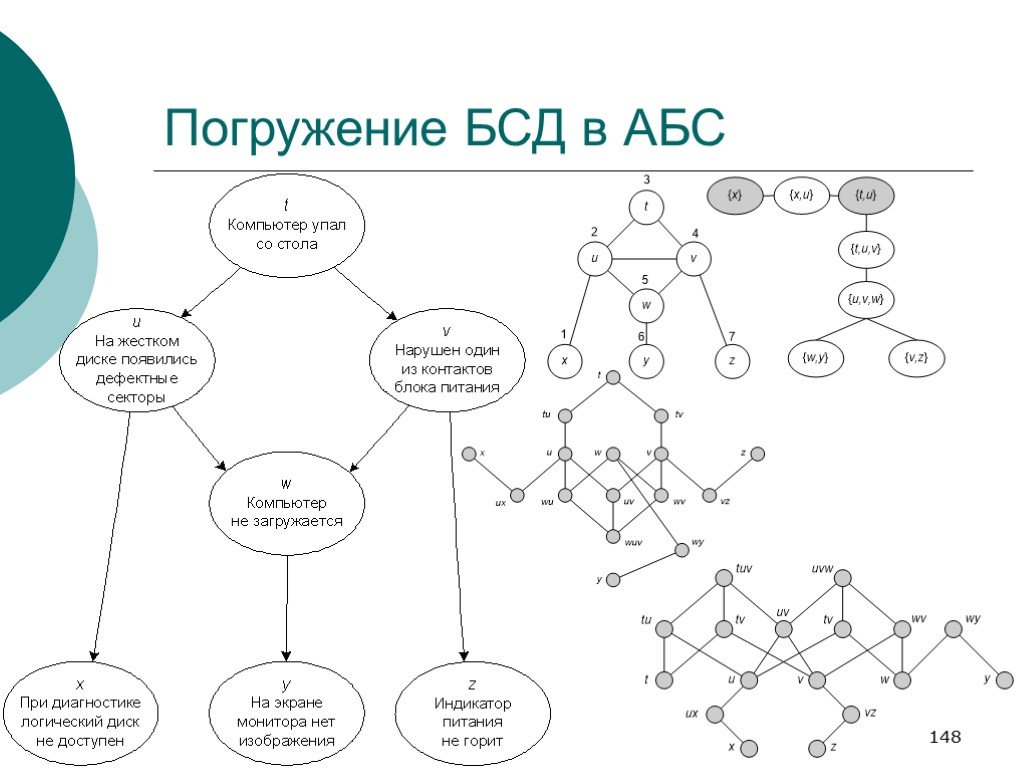
Слайд 138Результат погружения
Мы можем получить оценки (возможно интервальные) на всевозможные конъюнкции положительно означенных элементов. Мы можем выяснить, что имеющиеся оценки не соответствуют аксиоматике вероятностной логики.
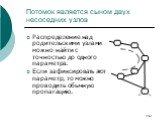
Слайд 139Направленный цикл с потомками
Потомок имеет одного родителя из цикла; Потомок является сыном двух соседних узлов; Потомок является сыном двух не соседних узлов; Потомок является сыном трех и более узлов.
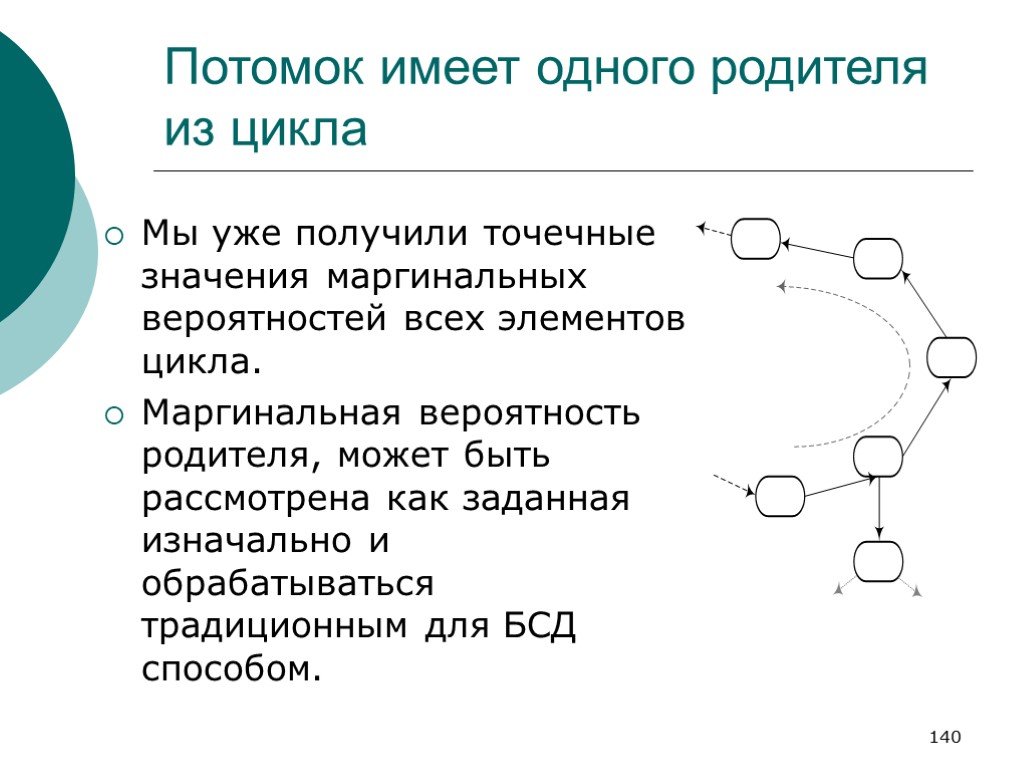
Слайд 140Потомок имеет одного родителя из цикла
Мы уже получили точечные значения маргинальных вероятностей всех элементов цикла. Маргинальная вероятность родителя, может быть рассмотрена как заданная изначально и обрабатываться традиционным для БСД способом.
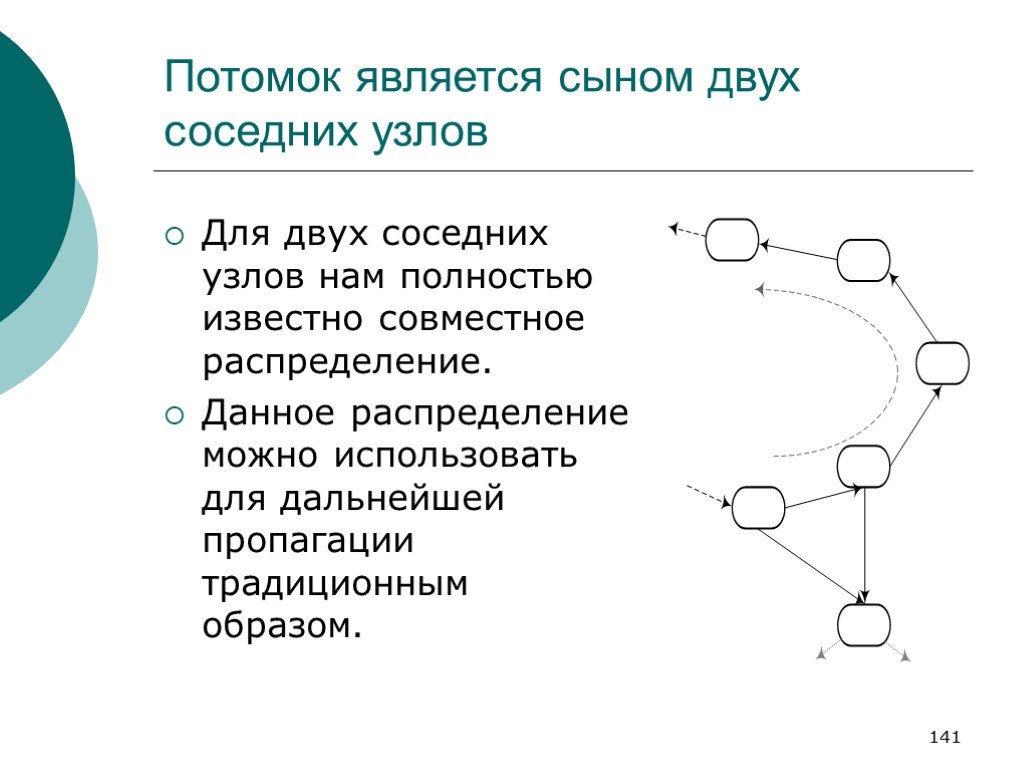
Слайд 141Потомок является сыном двух соседних узлов
Для двух соседних узлов нам полностью известно совместное распределение. Данное распределение можно использовать для дальнейшей пропагации традиционным образом.
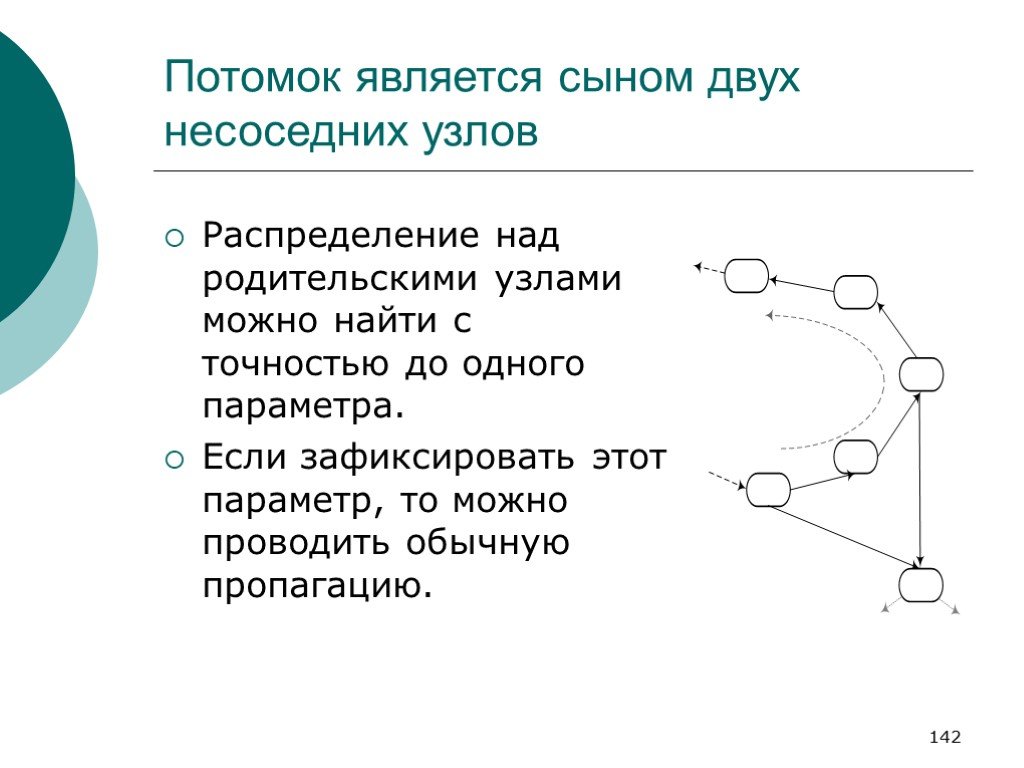
Слайд 142Потомок является сыном двух несоседних узлов
Распределение над родительскими узлами можно найти с точностью до одного параметра. Если зафиксировать этот параметр, то можно проводить обычную пропагацию.
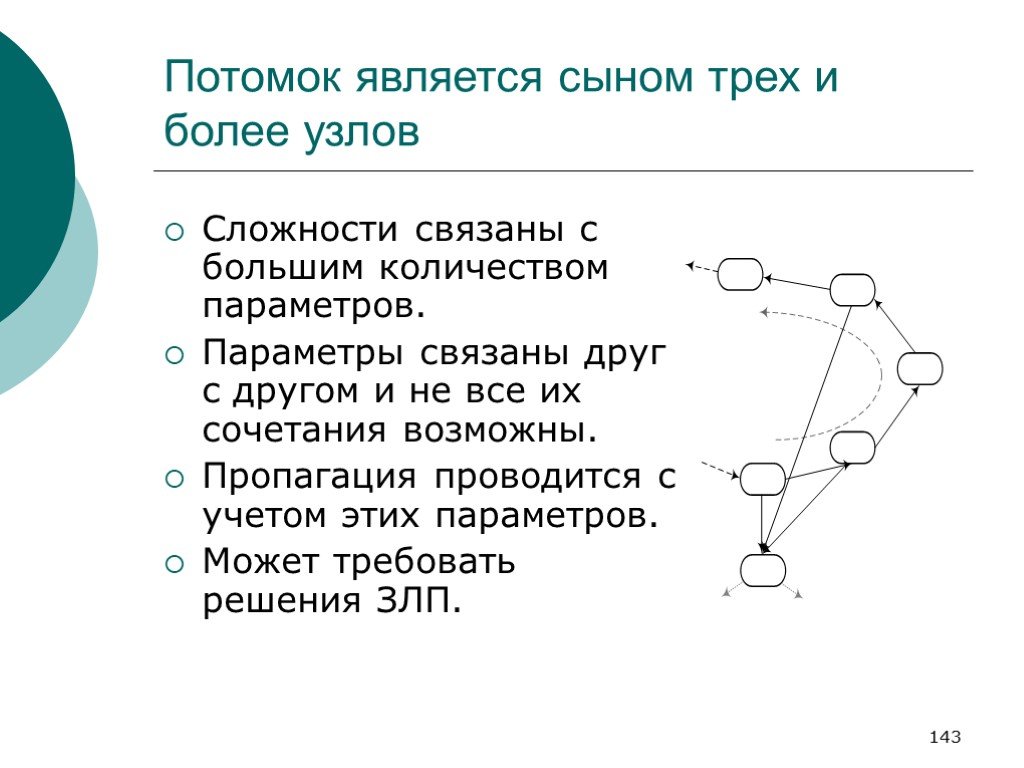
Слайд 143Потомок является сыном трех и более узлов
Сложности связаны с большим количеством параметров. Параметры связаны друг с другом и не все их сочетания возможны. Пропагация проводится с учетом этих параметров. Может требовать решения ЗЛП.
Слайд 144Учет влияния предков
Главная проблема – нельзя выписать систему линейных уравнений. Причина – нельзя зная условную вероятность относительно двух узлов, редуцировать ее до условной вероятности одного из них.
Слайд 145Путь решения
Можно зафиксировать все возможные означивания родителей. Для каждого означивания мы получаем изолированный цикл. Проводим обработку цикла и производим суммирование с учетом вероятности каждого конкретного означивания родителей.
Слайд 146Проблема
Возможна ситуация, когда при одних означиваниях цикл непротиворечив, а при других противоречив.
Слайд 147Возможное решение
Исключить «плохие» означивания родителей. Пересчитать байесовскую сеть доверия с учетом «невозможных» состояний.
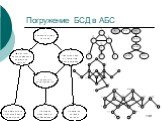
Слайд 148Погружение БСД в АБС
Слайд 149
Слайд 150Базовые дисциплины
Математические Математическая логика Теория вероятностей Экстремальные задачи Информатика Теория графов Представление данных Базы данных Искусственный интеллект Представление неопределенности Логико-вероятностный вывод Мягкие вычисления
Слайд 151Особенности материала
Части материала «масштабируются» под нужды конкретного курса и конкретной аудитории; В возникающих экстремальных задачах используются объекты, знакомые математикам (а не насильно заимствованные из экономики); Много задач для программирования, удобно для организации семинаров и практикумов; «Неисчерпаемая тематика» для курсовых и дипломных работ
Слайд 152Полезные навыки
Для изучения математической статистики (и способов ее применения на практике); Для дальнейшего овладения теорией надежности (структурно сложных систем в рамках ЛВМ и родственных ему) Для освоения аппаратов небайесовских мер истинности
Слайд 153
Слайд 154Монография
Тулупьев А.Л., Николенко С.И., Сироткин А.В. Байесовские сети: логико-вероятностный подход СПб.: Наука, 2006 607 стр. ISBN 5-02-025107-0 Изд. грант РФФИ 06-01-14108
Слайд 156Разворот обложки
Слайд 157Дополнительный материал
Слайд 158Мягкие вычисления (SC)
Консорциум вычислительных методологий, которые коллективно обеспечивают основы для понимания, конструирования и развития интеллектуальных систем
Заде Л.А. Роль мягких вычислений в понимании, конструировании и развитии информационных/интеллектуальных систем // Новости искусственного интеллекта. 2001. 2—3 (44—45).
Слайд 159Мягкие вычисления: отрасли
Нечеткая логика (FL) Нейровычисления (NC) Генетические вычисления (GC) Вероятностные вычисления (PC) Рассуждения на базе свидетельств (ER) [Байесовские сети] (BN) Хаотические системы (ChS) Машинное обучение (ML)
Слайд 160Цель и задачи исследования
Слайд 161Декомпозируемость знаний
Эксперт не мыслит о закономерностях предметной области как о «связи всего со всеми» Выделяются фрагменты знаний (Knowledge patterns), которые содержат достаточно подробные сведения о небольшом числе объектов (или утверждений) о предметной области, а также о связях между ними
Слайд 162Модель утверждения
Атомарная пропозициональная формула (булевская переменная, пропозициональная переменная, атомарная пропозиция) --- модель «атомарного» утверждения о предметной области Пропозициональные формулы --- модели утверждений, возможно сложных, о предметной области
Слайд 163Неопределенность
Почему возникает Пропущенные наблюдения Неточность средств измерения Экспертные высказывания Неудачные регистрационные формы Частично незаполненное поле (только год в дате рождения) … Как проявляется Нужно ли обрабатывать
Слайд 164Виды неопределенности
Существует много видов, например неоднозначность и многозначность слов; возможность двух или более интерпретаций записи даже на формальном языке; недетерминированность; нечёткость (в т.ч. лингвистическая); неточность (интервальные оценки); недоопределённость...
Слайд 165Неопределенность утверждения
Истинностное означивание и мера истинности Мера истинности как степень доверия к утверждению Мера истинности как степень тесноты связи между частями составной пропозициональной формулы Возможные значения и оценки меры истинности
Слайд 166Объект исследования
Высказывания, суждения, утверждения, представимые пропозициональными формулами над булевскими переменными; Мера истинности которых характеризуется количественно с помощью вероятностных и/или небайесовских оценок; Которые могут быть как точечные, так и интервальные [а в перспективе – твинные].
Слайд 167Предмет исследования
Базы фрагментов знаний с неопределённостью; Фрагмент знаний – некоторая [математическая] структура, состоящая из небольшого набора «тесно связанных» пропозициональных формул; Мера истинности которых и теснота связи охарактеризована: тензором условных вероятностей – БСД; представлением тензора совместных вероятностей, допускающим точечные и интервальные оценки --- АБС; [обобщение последнего на небайесовские меры истинности: нечёткую, доверия-правдоподобия, необходимости-возможности...]
Слайд 168Логико-вероятностный подход (ЛВП)
Вероятностная мера как мера истинности Точечные оценки значений вероятностной меры Интервальные оценки значений вероятностной меры (как следствие неопределенности) «Интервальная вероятность» и интервальная оценка вероятности Единственность распределения и семейство распределений вероятности
Слайд 169ЛВП --- богатая история
G. Boole, “An Investigation of the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probabilities” (1854) N. Nilsson, Probabilistic Logic (AI, 1986) N. Nilsson, Probabilistic Logic Revisited (AI, 1993) De Finetti, Whaley, Ramsay, … Школа логико-вероятностных методов в теории надежности (рук. адм. И. А. Рябинин) --- важнейшие приложения ЛВП.
Слайд 170Непротиворечивость
Согласованность, согласуемость, программный код
Слайд 171Пример ограничений:
Слайд 172Программный код на C++
for (i = 0; i
Слайд 173непротиворечив, (является распределением вероятностей) если он удовлетворяет условиям типа
Непротиворечивое распределение
Мы будем говорить, что набор оценок
Слайд 174Фрагмент знаний Идеал конъюнктов:
Ограничения на вероятность истинности:
Эти ограничения будем обозначать .
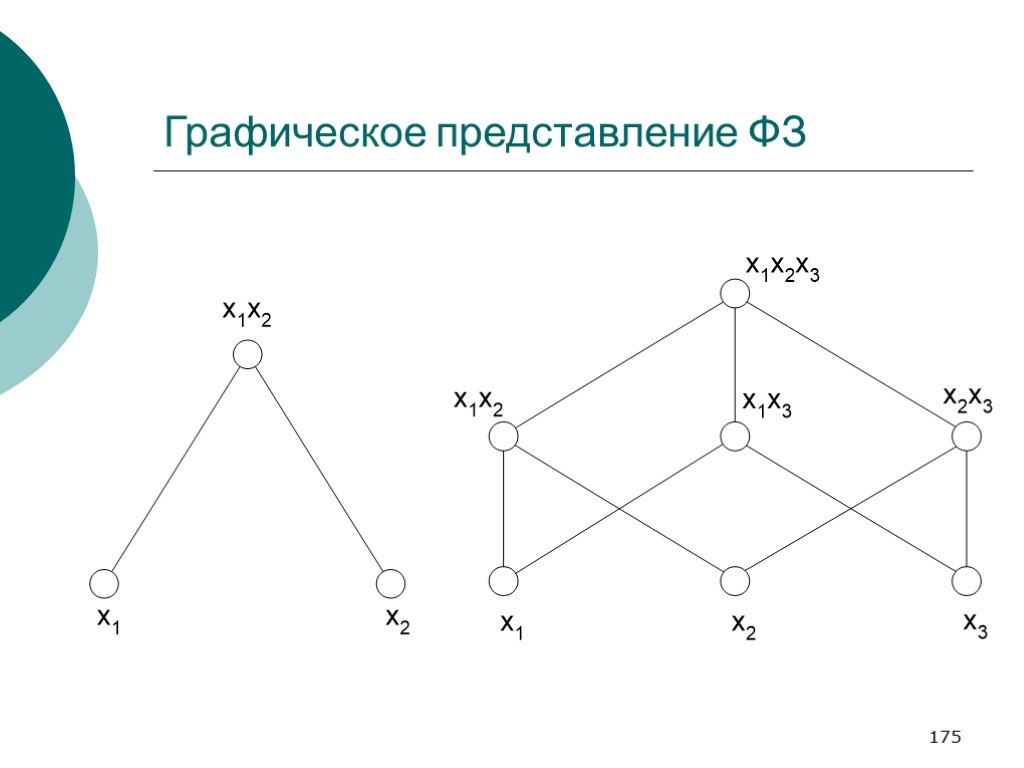
Слайд 175Графическое представление ФЗ
Слайд 176Непротиворечивость (согласованность) ФЗ
Фрагмент знаний непротиворечив, если
существует непротиворечивое распределение :
Слайд 177Согласуемость ФЗ
ФЗ называется согласуемым, если существует хотя бы одно непротиворечивое распределение
такое, что
Слайд 178Поддержание непротиворечивости
Для того чтобы получить из согласуемого ФЗ согласованный, требуется решить ряд задач линейного программирования.
Для каждого по две:
Слайд 179Дополнительные сведения
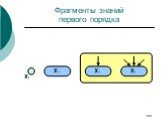
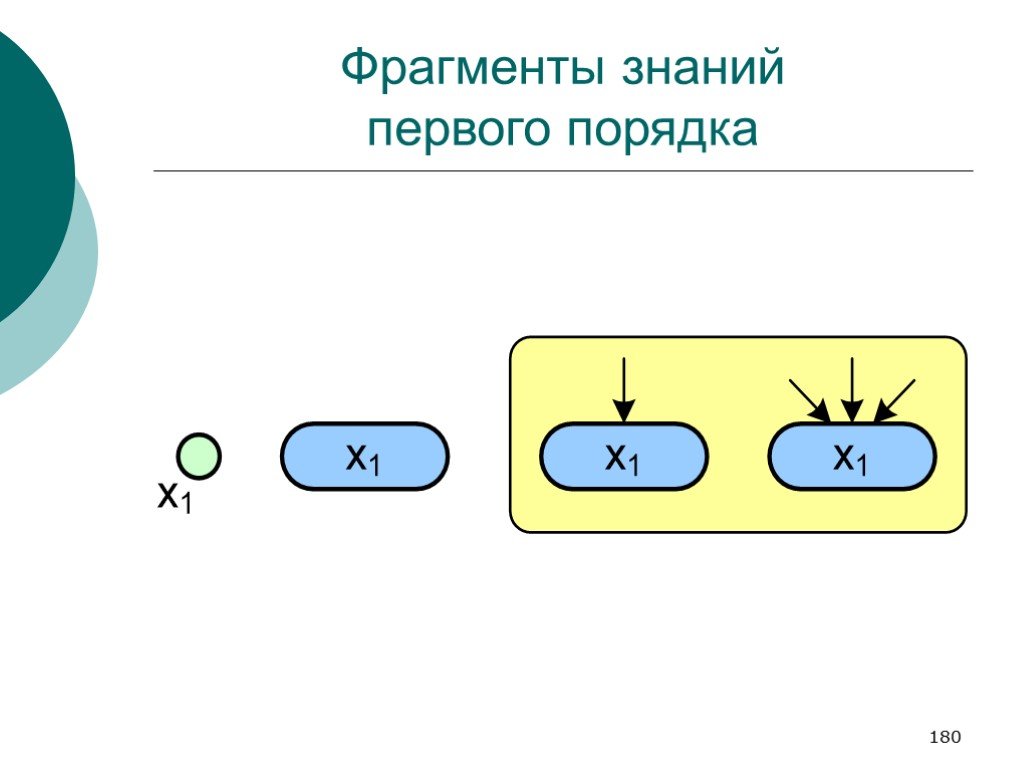
Слайд 180Фрагменты знаний первого порядка
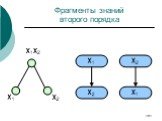
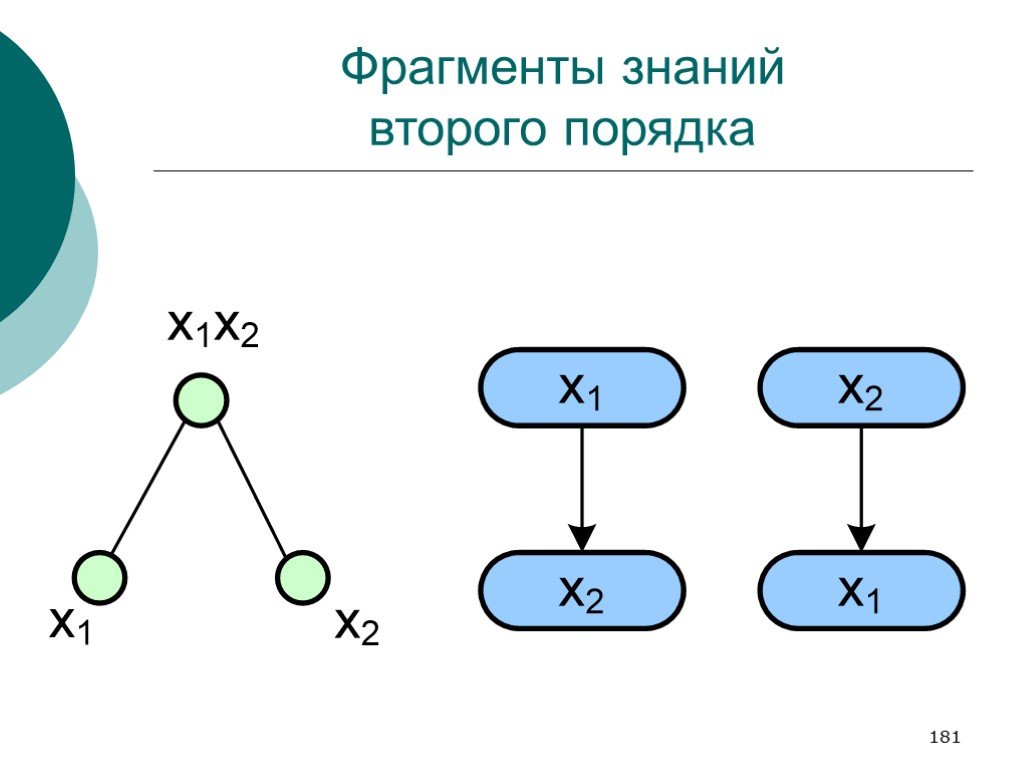
Слайд 181Фрагменты знаний второго порядка
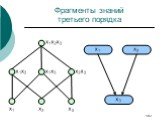
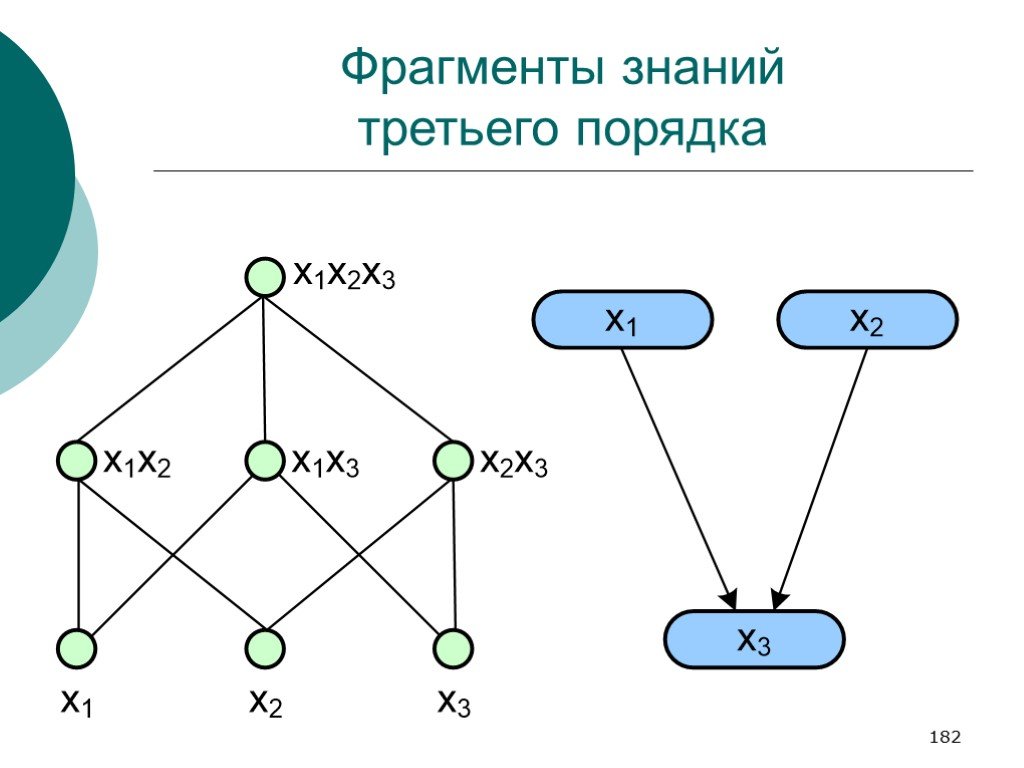
Слайд 182Фрагменты знаний третьего порядка
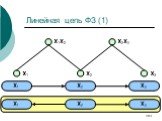
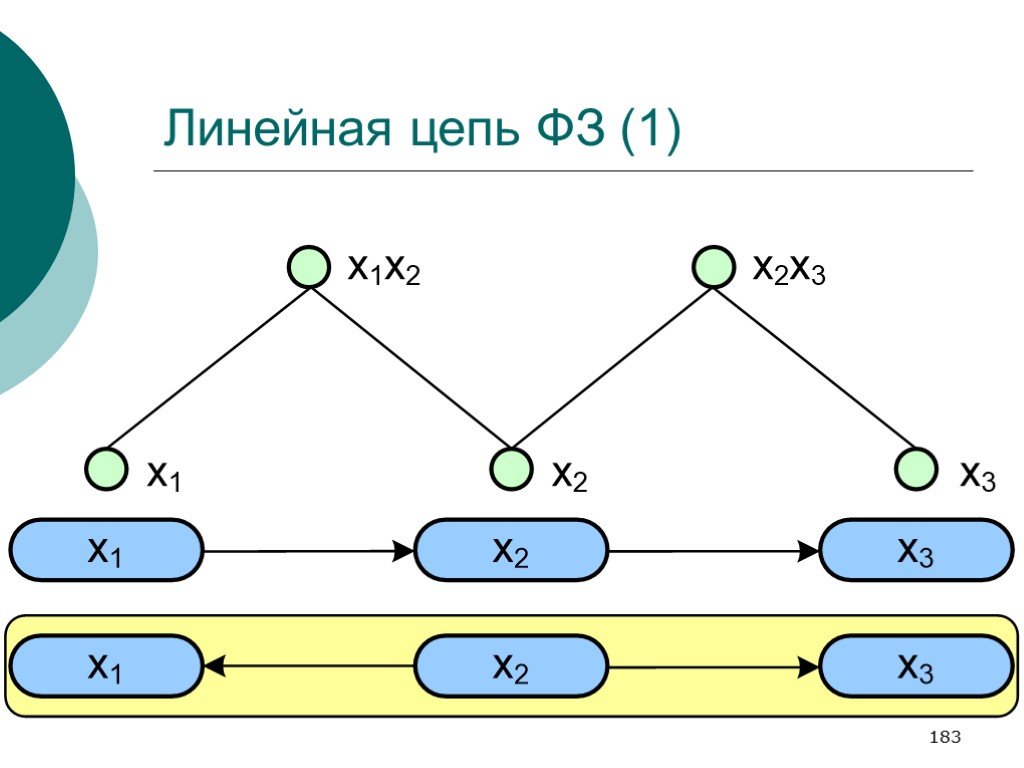
Слайд 183Линейная цепь ФЗ (1)
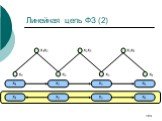
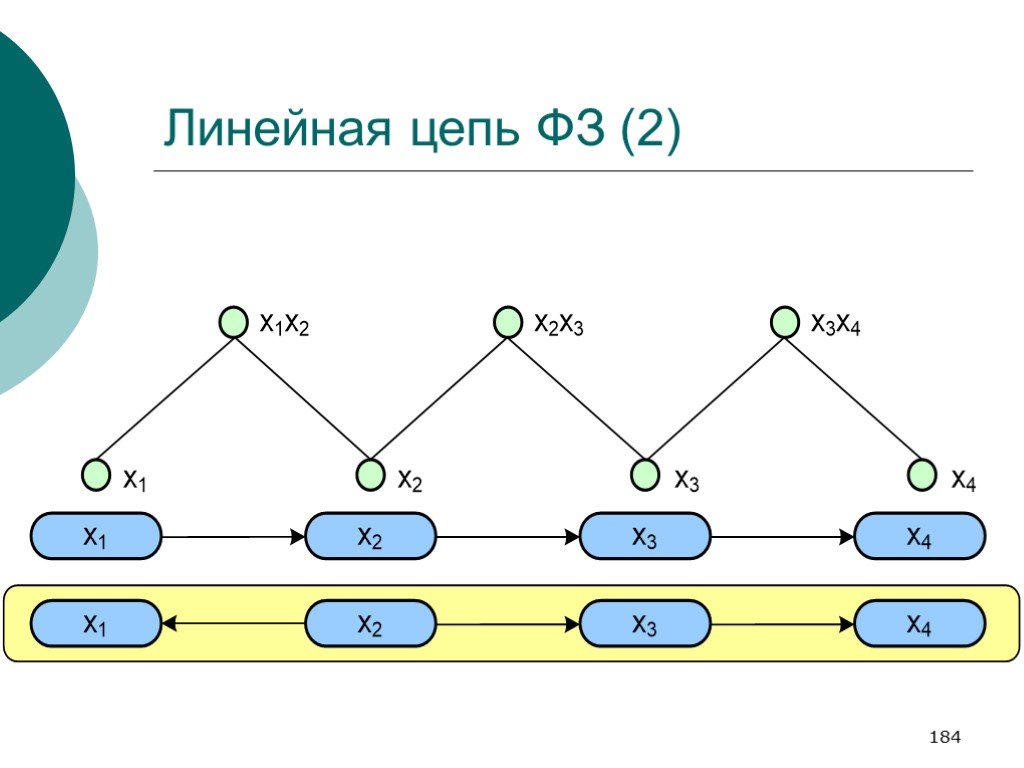
Слайд 184Линейная цепь ФЗ (2)













































































































































![БС применяются в медицине. Для быстрой постановки диагноза, чтобы выбрать правильное учреждение для госпитализации Для дифференциальной диагностики заболеваний, симптоматические проявления которых сходны [но не совпадают полностью] БС применяются в медицине. Для быстрой постановки диагноза, чтобы выбрать правильное учреждение для госпитализации Для дифференциальной диагностики заболеваний, симптоматические проявления которых сходны [но не совпадают полностью]](https://prezentacii.org/upload/cloud/18/05/50532/images/thumbs/screen16.jpg)




















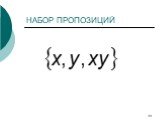




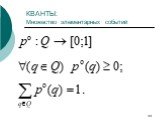












![«Интервальная» непротиворечивость. p(x)=[0.4;0.5] p(x)=[0.5;0.6] непротиворечиво (согласовано, совместно). p(x)=[0.7;0.8] p(x)=[0.5;0.6] противоречиво (несовместно) p(x)=[0.3;0.5] p(x)=[0.4;0.6] непротиворечиво (не согласовано, совместно) «Интервальная» непротиворечивость. p(x)=[0.4;0.5] p(x)=[0.5;0.6] непротиворечиво (согласовано, совместно). p(x)=[0.7;0.8] p(x)=[0.5;0.6] противоречиво (несовместно) p(x)=[0.3;0.5] p(x)=[0.4;0.6] непротиворечиво (не согласовано, совместно)](https://prezentacii.org/upload/cloud/18/05/50532/images/thumbs/screen58.jpg)



![ФЗ с [,]-ми оценками. Задан набор интервальных оценок, который мы обозначим как D(n). ФЗ с [,]-ми оценками. Задан набор интервальных оценок, который мы обозначим как D(n).](https://prezentacii.org/upload/cloud/18/05/50532/images/thumbs/screen63.jpg)
![Непротиворечивость ФЗ ([]). Пусть задан набор интервальных оценок. Этот набор непротиворечив (согласован), если для произвольного элемента при выборе произвольной точки из интервальной оценки в остальных интервалах можно выбрать точки так, что получившийся набор точечных оценок непротиворечив. Непротиворечивость ФЗ ([]). Пусть задан набор интервальных оценок. Этот набор непротиворечив (согласован), если для произвольного элемента при выборе произвольной точки из интервальной оценки в остальных интервалах можно выбрать точки так, что получившийся набор точечных оценок непротиворечив.](https://prezentacii.org/upload/cloud/18/05/50532/images/thumbs/screen64.jpg)
![Поддержание непротиворечивости ФЗ в [,]-ом случае Поддержание непротиворечивости ФЗ в [,]-ом случае](https://prezentacii.org/upload/cloud/18/05/50532/images/thumbs/screen65.jpg)

![Апостериорный вывод в ФЗ АБС. Мы что-то узнали: поступило свидетельство; Как оно повлияет на наши оценки вероятностей утверждений из нашей базы знаний; [Как распространить влияние свидетельства] Несколько вычислительно разных ситуаций... Апостериорный вывод в ФЗ АБС. Мы что-то узнали: поступило свидетельство; Как оно повлияет на наши оценки вероятностей утверждений из нашей базы знаний; [Как распространить влияние свидетельства] Несколько вычислительно разных ситуаций...](https://prezentacii.org/upload/cloud/18/05/50532/images/thumbs/screen67.jpg)



![Апостериорный вывод: (.) и [,]. Вид оценок в ФЗ, куда поступает свидетельство, также создают особый вычислительный аспект: точечные оценки --- «прямые» вычисления по определению условной вероятности; интервальные оценки --- задачи гиперболического программирования. Апостериорный вывод: (.) и [,]. Вид оценок в ФЗ, куда поступает свидетельство, также создают особый вычислительный аспект: точечные оценки --- «прямые» вычисления по определению условной вероятности; интервальные оценки --- задачи гиперболического программирования.](https://prezentacii.org/upload/cloud/18/05/50532/images/thumbs/screen71.jpg)

![Апостериорный вывод, ФЗ с [,]. Сведение: Апостериорный вывод, ФЗ с [,]. Сведение:](https://prezentacii.org/upload/cloud/18/05/50532/images/thumbs/screen74.jpg)



























![Что нам дают такие предположения. Независимость d-разделимых [переменных в узлах] позволяет выделить единственное распределение из всех, для которых подходят заданные условные вероятности. Это единственное распределение -- произведение всех вероятностей, заданных в БСД (chain rule). Что нам дают такие предположения. Независимость d-разделимых [переменных в узлах] позволяет выделить единственное распределение из всех, для которых подходят заданные условные вероятности. Это единственное распределение -- произведение всех вероятностей, заданных в БСД (chain rule).](https://prezentacii.org/upload/cloud/18/05/50532/images/thumbs/screen114.jpg)








![Если моральный граф триангулярен. То его можно разбить на клики, которые затем можно объединить в дерево смежностей (разными вариантами). Каждая максимальная клика попадает в отдельный [соответствующий ей] узел дерева смежности. Если моральный граф триангулярен. То его можно разбить на клики, которые затем можно объединить в дерево смежностей (разными вариантами). Каждая максимальная клика попадает в отдельный [соответствующий ей] узел дерева смежности.](https://prezentacii.org/upload/cloud/18/05/50532/images/thumbs/screen124.jpg)



























![Мягкие вычисления: отрасли. Нечеткая логика (FL) Нейровычисления (NC) Генетические вычисления (GC) Вероятностные вычисления (PC) Рассуждения на базе свидетельств (ER) [Байесовские сети] (BN) Хаотические системы (ChS) Машинное обучение (ML) Мягкие вычисления: отрасли. Нечеткая логика (FL) Нейровычисления (NC) Генетические вычисления (GC) Вероятностные вычисления (PC) Рассуждения на базе свидетельств (ER) [Байесовские сети] (BN) Хаотические системы (ChS) Машинное обучение (ML)](https://prezentacii.org/upload/cloud/18/05/50532/images/thumbs/screen159.jpg)







![Предмет исследования. Базы фрагментов знаний с неопределённостью; Фрагмент знаний – некоторая [математическая] структура, состоящая из небольшого набора «тесно связанных» пропозициональных формул; Мера истинности которых и теснота связи охарактеризована: тензором условных вероятностей – БСД; предста Предмет исследования. Базы фрагментов знаний с неопределённостью; Фрагмент знаний – некоторая [математическая] структура, состоящая из небольшого набора «тесно связанных» пропозициональных формул; Мера истинности которых и теснота связи охарактеризована: тензором условных вероятностей – БСД; предста](https://prezentacii.org/upload/cloud/18/05/50532/images/thumbs/screen167.jpg)