Презентация "Статистическое изучение взаимосвязей" – проект, доклад

Статистическое изучение взаимосвязей

Основные методы изучения связей

Для выявления наличия связи, ее характера и направления в статистике используются методы: метод приведения параллельных данных (метод параллельных рядов) основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и ее характер. К простейшим показателям степени тесноты связи относят коэффициент корреляции знаков, предложенный немецким ученым Г. Фехнером. где С - число случаев совпадения знаков отклонений, Н - число случаев несовпадения знаков отклонений Этот коэффициент принимает значения от +1 (знаки всех отклонений совпадают - прямая связь) до -1 ( знаки всех отклонений не совпадают - обратная связь). балансовый метод используется для характеристики взаимосвязи между производством и реализацией продукции, денежными доходами и расходами населения и т.д. корреляционный анализ заключается в количественном определении тесноты связи между признаками. регрессионный анализ заключается в определении аналитического выражения связи между признаками.

метод аналитических группировок - изменения средних или относительных значений результативного признака сопоставляются с изменением факторного признака для выявления характера связи; графический метод заключается в построении и анализе поля корреляции. Поле корреляции (диаграмма рассеяния) – это совокупность точек (xi, yi) на плоскости (xi - значения факторного признака, yi – соответствующие значения результативного признака). парная регрессия характеризует связь между двумя признаками: результативным Y и факторным X. множественная (многофакторная) регрессия характеризует связь между результативным Y и несколькими факторными признаками X1, X2, …,Xk.

Метод аналитической группировки

Метод аналитической группировки применяется в случаях, когда совокупность достаточно велика и параллельные ряды не позволяют обнаружить зависимость. Этот метод – это разбиение исходных данных на группы в соответствии со значением признака фактора и расчет для каждой группы соответствующего среднегруппового значения результативного признака с тем, чтобы обнаружить взаимосвязь. Аналитические группировки обычно используются для однородных совокупностей, поэтому в них применяются чаще всего равные интервалы. Пример: зависимость между суммой товарооборота магазина и уровнем издержек обращения . Группировка показывает, что с ростом товарооборота падает значение результативного признака. Налицо обратная зависимость.

Если изобразить результаты группировки на графике, получим эмпирическую линию регрессии . Интервалы значений факторного признака заменяются средними групповыми показателями. Эмпирическая линия регрессии показывает примерную форму и направление взаимосвязи. При построении аналитической группировки надежность ее результатов зависит от того, какое число групп мы можем выделить в предполагаемом характере взаимосвязи. Помимо эмпирической линии регрессии, непосредственно определяющей форму и направление взаимосвязей, существует корреляционное поле, на котором отражаются параметрические данные. По корреляционному полю так же можно судить о характере взаимосвязи. Если точки сконцентрированы около диагонали идущей слева направо, снизу вверх – то связь прямая. Если около другой диагонали – обратная. Если точки рассеяны по всему полю графика – связь отсутствует. При построении аналитической группировки важно правильно определить величину интервала. Если в результате первичной группировки связь не проявляется отчетливо, можно укрупнить интервал. Однако, при построении аналитической группировки руководствуемся правилом: чем больше групп мы можем выделить, не натолкнувшись ни на одно исключение, тем надежнее наша гипотеза о наличии и форме связи.

Графический метод выявления корреляционных зависимостей

Существующая связь между исследуемыми признаками наглядно представляется на графиках. Нанеся на график точки, соответствующие значениям X, Y, получим корреляционное поле, где по характеру расположения точек можно судить о направлении и силе связи. В системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат - результативного. Каждое пересечение линий, проводимых через эти оси, обозначаются точкой. При отсутствии тесных связей имеет место беспорядочное распо­ложение точек на графике. Чем сильнее связь между признаками, тем теснее будут груп­пироваться точки вокруг определенной линии, выражающей форму связи.

Методы изучения связи социальных явлений

Важной задачей статистики является разработка методики статистической оценки социальных явлений, которая осложняется тем, что многие социальные явления не имеют количественной оценки. Количественная оценка связей социальных явлений осуществляется на основе расчета и анализа целого ряда коэффициентов

Причинность, регрессия, корреляция

Исследование объективно существующих связей между явлениями – важнейшая задача теории статистики. В процессе статистического исследования зависимостей выявляются причинно-следственные отношения между явлениями, что позволяет выявить факторы (признаки), оказывающие основное влияние на вариацию изучаемых явлений и процессов. Признаки по их значению для изучения взаимосвязи делятся на два класса: Факторные - признаки, вызывающие изменение других, связанных с ними признаков. Результативные - признаки, изменяющиеся под действием факторных признаков.

Виды статистической зависимости

В статистике различают функциональную и стохастическую зависимости. Функциональной называется зависимость, при которой определенному значению факторного признака соответствует одно значение результативного. Функциональная связь обычно выражается формулами: S=2R; Y= aX + b Стохастической называется зависимость, при которой причинная связь проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений. Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков. Y =  (x) +  При корреляционной связи устанавливается такое соотношение, в котором определенному изменению факторного признака соответствует среднее изменение признака результативного. Широкое варьирование результативного признака объясняется разнообразием факторов, не поддающихся строгому учету и контролю. Характерные особенности корреляционных связей: 1.Они проявляются не в единичных случаях, а требуют для своего исследования массовых наблюдений. 2. Корреляционные связи являются неполными. Поэтому даже на массовом материале, где случайные факторы сглаживаются, зависимости не будут носить полного характера, т.е. функционального характера.

Классификация связи между явлениями и их признаками по направлению

По направлению выделяют связь прямую и обратную. Прямая связь – это связь, при которой с увеличением или уменьшением значений факторного признака увеличиваются или уменьшаются значения результативного. Пример. Рост производительности труда способствует увеличению уровня рентабельности производства. Обратная связь – это связь, при которой с увеличением или уменьшением значений факторного признака уменьшаются или увеличиваются значения результативного. Пример. С увеличением уровня фондоотдачи снижается себестоимость единицы производимой продукции.

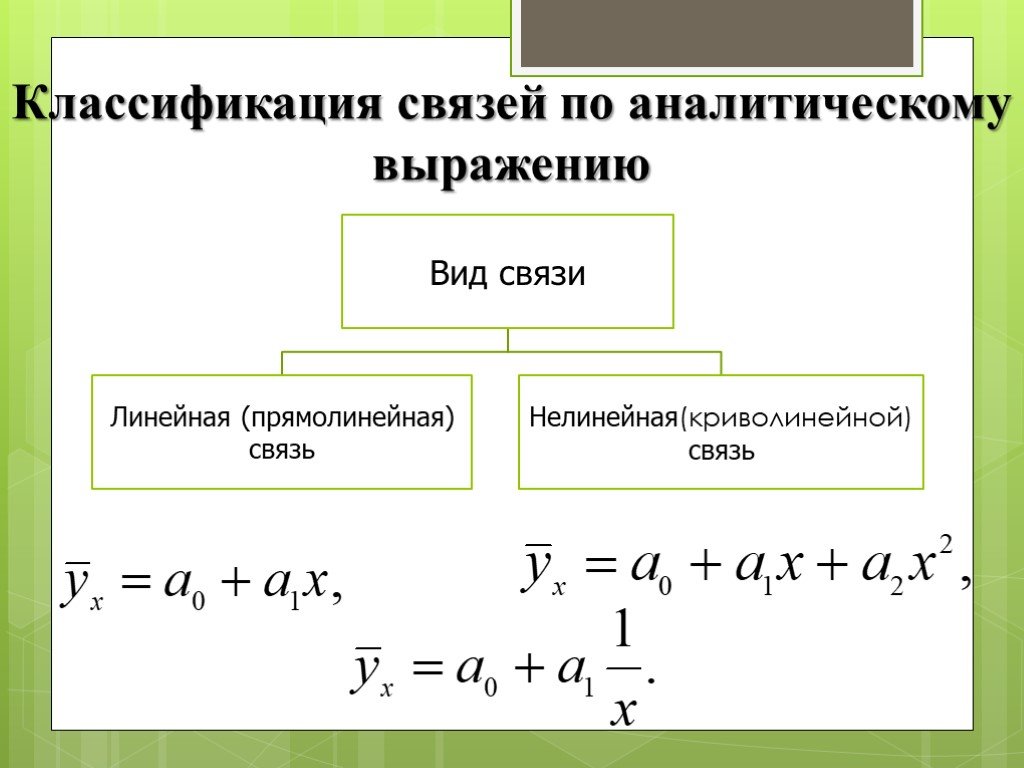
Классификация связей по аналитическому выражению

Линейный коэффициент корреляции (r) служит для определения степени тесноты парной линейной зависимости.

Классификация линейной связи по степени тесноты

или