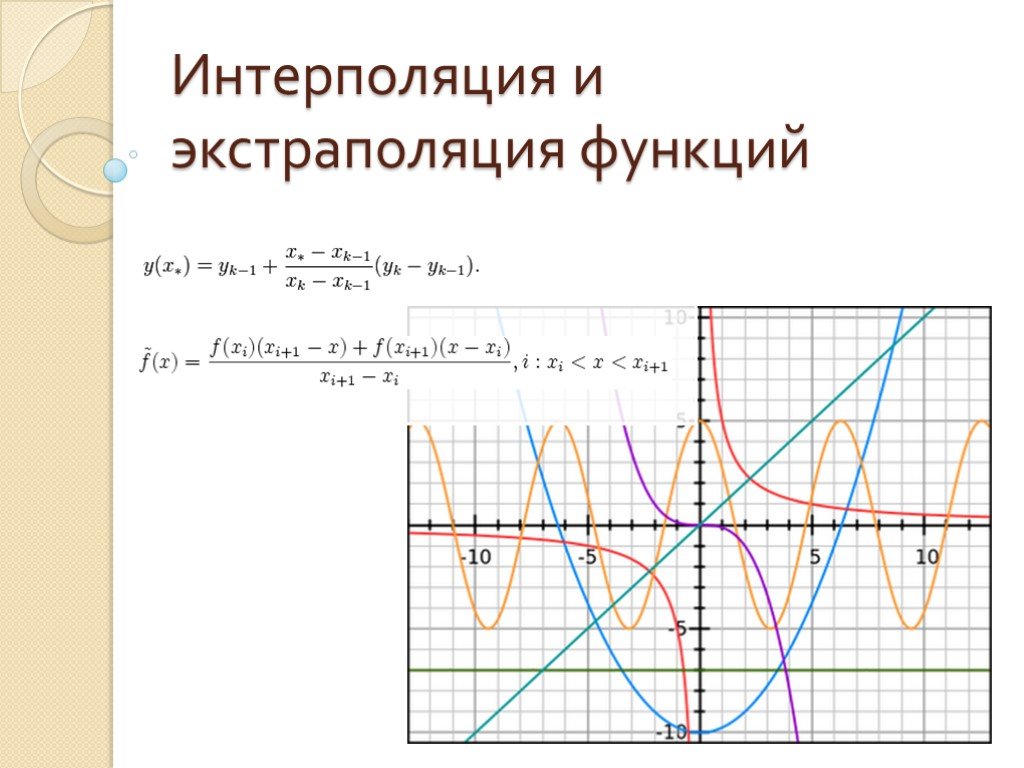
Слайд 1Интерполяция и экстраполяция функций
Слайд 2Табличное задание функции При алгебраической интерполяции для представления информации о функции f(x) используется таблица значений этой функции:
Алгебраическая интерполяция
Для интерполирования функций с большим числом узлов, применяют локальную интерполяцию. Для этого заданную сетку делят на несколько интервалов с небольшим числом узлов и на каждом из интервалов строят свой интерполяционный полином, поэтому локальную интерполяцию еще называют кусочно-полиномиальной.

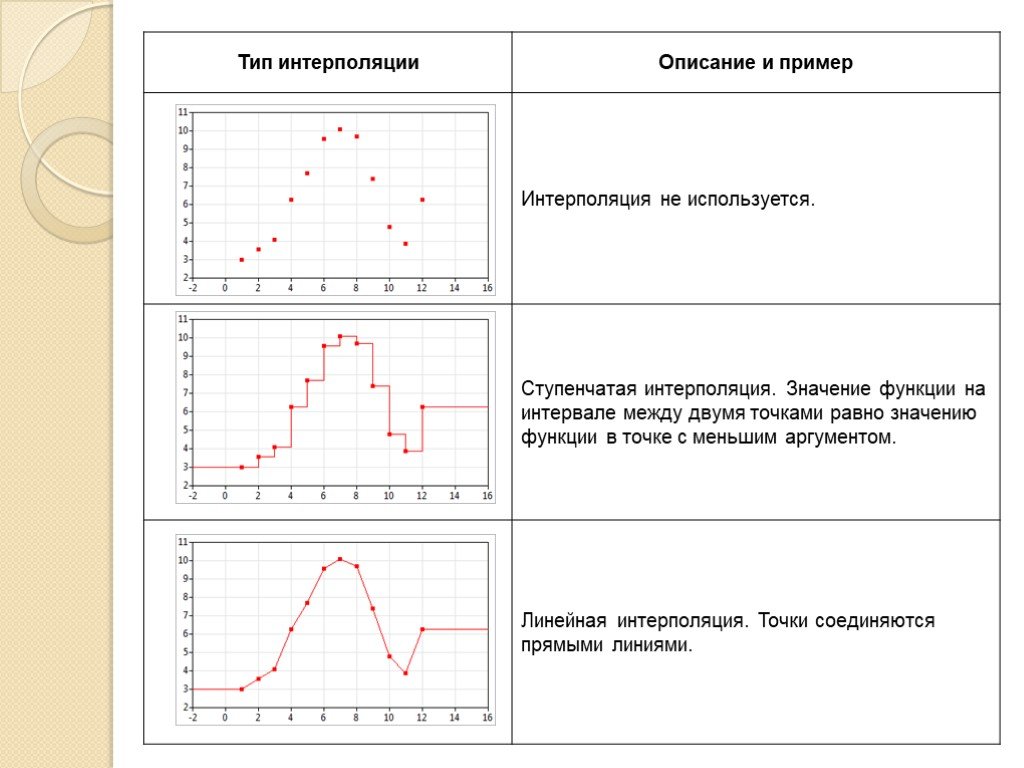
Слайд 3Простейшие способы интерполяции Простейшим способом интерполяции функции f по таблице является ступенчатая интерполяция. Один из ее вариантов формулируется так: То есть за значение функции берется значение функции f(x) в точке, ближайшей к рассматриваемой. Более точным способом интерполяции является кусочно-линейная интерполяция. При таком подходе значение f(x) интерполируется по двум соседним с точкой x точкам. (здесь подразумевается монотонное возрастание последовательности xi) Интересно понять, с какой точностью интерполяционные формулы аппроксимируют функцию f. Предположим, что производная функции f ограничена величиной g. Тогда на отрезке [xi,xi + 1] функция f не может отклониться от линейной интерполяции более, чем на
Слайд 4
Слайд 5Интерполяционные полиномы Алгебраическим интерполяционным многочленом Pn(x, f, x0,..., xn) называется многочлен Pn(x) = c0 + c1x + c2x2 + ... + cnxn степени не выше n, принимающий в точках x0, x1,..., xn значения f(x0), f(x1),..., f(xn) Теорема. Если заданы попарно различные узлы x0, x1, x2,..., xn и значения f(x0), f(x1),..., f(xn), то алгебраический интерполяционный многочлен существует и единственен. Доказательство Сначала докажем, что существует не более чем один интерполяционный многочлен, а затем построим его. Если бы их было два, то их разность - многочлен степени не больше n, обращалась бы в 0 в n + 1 точке - x0, x1,..., xn, что невозможно для ненулевого многочлена. В качестве примера интерполяционного многочлена можно привести Интерполяционный многочлен Лагранжа.

Слайд 6Жозе́ф Луи́ Лагра́нж (фр. Joseph Louis Lagrange, итал. Giuseppe Lodovico Lagrangia; 25 января 1736, Турин — 10 апреля 1813, Париж) —французский математик, астроном и механик итальянского происхождения. Наряду с Эйлером — лучший математик XVIII века. Особенно прославился исключительным мастерством в области обобщения и синтеза накопленного научного материала. Автор классического трактата «Аналитическая механика», в котором установил фундаментальный «принцип возможных перемещений» и завершил математизацию механики. Внёс грандиозный вклад в развитие анализа, теории чисел, теорию вероятностей и численные методы, создал вариационное исчисление.
Титульный лист «Аналитической механики»

Слайд 7Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n + 1 пар чисел , где все xi различны, существует единственный многочлен L(x) степени не более n, для которого L(xi) = yi. В простейшем случае (n = 1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.
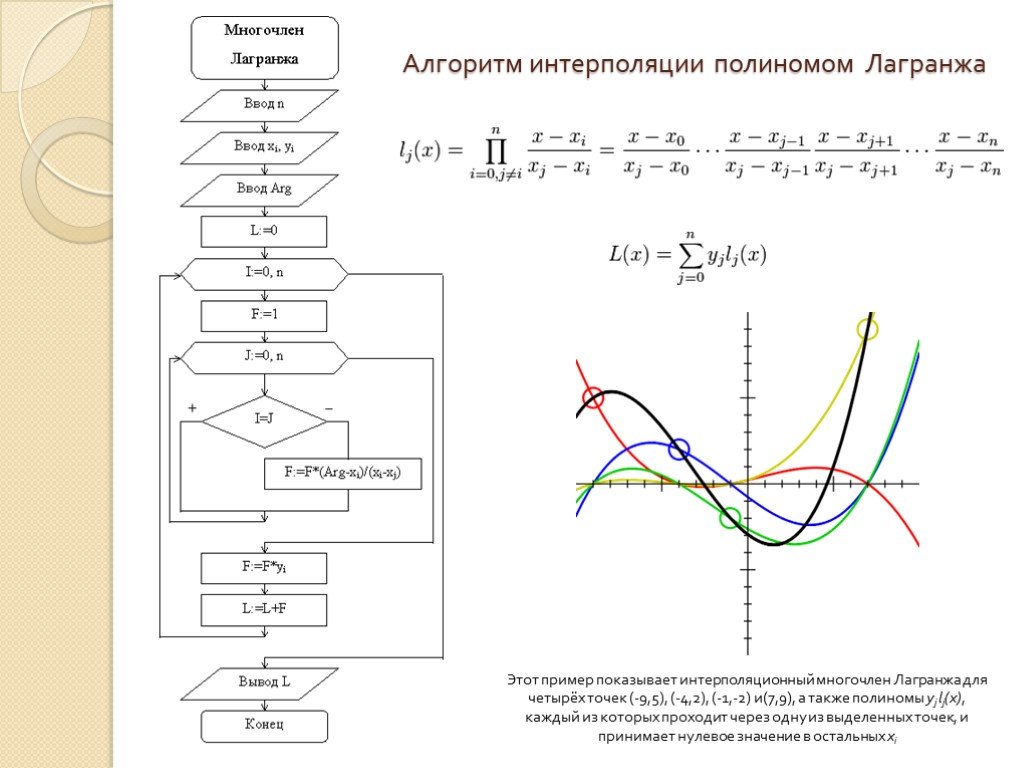
Лагранж предложил способ вычисления таких многочленов: где базисные полиномы определяются по формуле: lj(x) обладают следующими свойствами: являются многочленами степени n lj(xj) = 1 lj(xi) = 0 при i<>j Отсюда следует, что L(x), как линейная комбинация lj(x), может иметь степень не больше n, и L(xj) = yj.

Слайд 8Полиномы Лагранжа используются для интерполяции, а также для численного интегрирования. Пусть для функции f(x) известны значения yj = f(xj) в некоторых точках. Тогда мы можем интерполировать эту функцию как В частности, Значения интегралов от lj не зависят от f(x), и их можно вычислить заранее, зная последовательность xi.
Слайд 9Случай равномерного распределения узлов интерполяции В случае равномерного распределения узлов интерполяции xi выражаются через расстояние между узлами интерполяции h и начальную точку x0: и, следовательно, Подставив эти выражения в формулу базисного полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим Теперь можно ввести замену переменной и получить полином от y, который строится с использованием только целочисленной арифметики. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования длинной арифметики.
Слайд 10Алгоритм интерполяции полиномом Лагранжа
Этот пример показывает интерполяционный многочлен Лагранжа для четырёх точек (-9,5), (-4,2), (-1,-2) и(7,9), а также полиномы yj lj(x), каждый из которых проходит через одну из выделенных точек, и принимает нулевое значение в остальных xi
Слайд 11Погрешность интерполирования Пусть интерполяционный многочлен Лагранжа построен для известной функции f(x). Необходимо выяснить, насколько этот многочлен близок к функции в точках отрезка [a, b], отличных от узлов. Погрешность интерполяции равна |f(x) – Ln(x)|. Оценку погрешности можно получить на основании следующей теоремы. Теорема Пусть функция f(x) дифференцируема n +1 раз на отрезке [a, b], содержащем узлы интерполяции xi из [a, b], i = 0, 1, … , n. Тогда для погрешности интерполяции в точке x из [a, b] справедлива оценка:

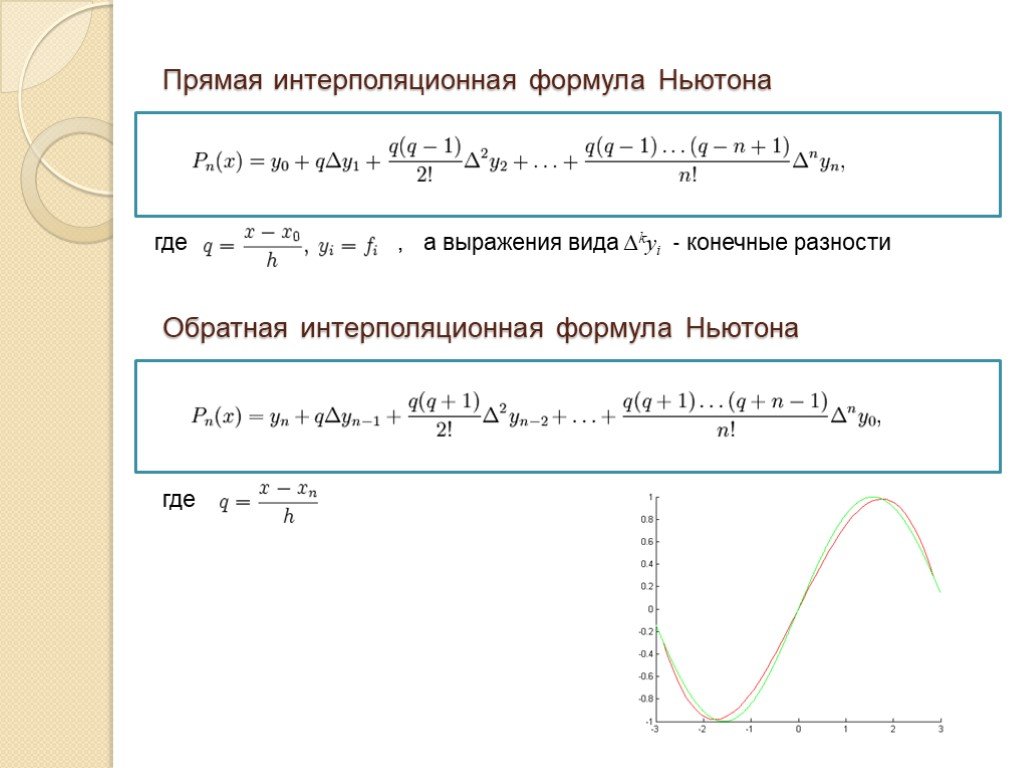
Слайд 13Интерполяционный многочлен в форме Ньютона Введем понятие разностного отношения. Разностным отношением нулевого порядка в точке xi назовем значение f(xi). Разностное отношение первого порядка определяется как А n+1-го порядка - рекурсивно через разностное отношение n-го порядка: Тогда можно показать, что интерполяционный многочлен может быть записан в следующей форме: Pn(x,f,x0,...,xn) = f(x0) + (x − x0)f(x0,x1) + ... + (x − x0)(x − x1)...(x − xn − 1)f(x0,...,xn)
Слайд 14где , а выражения вида Δkyi - конечные разности
Прямая интерполяционная формула Ньютона
Обратная интерполяционная формула Ньютона
где

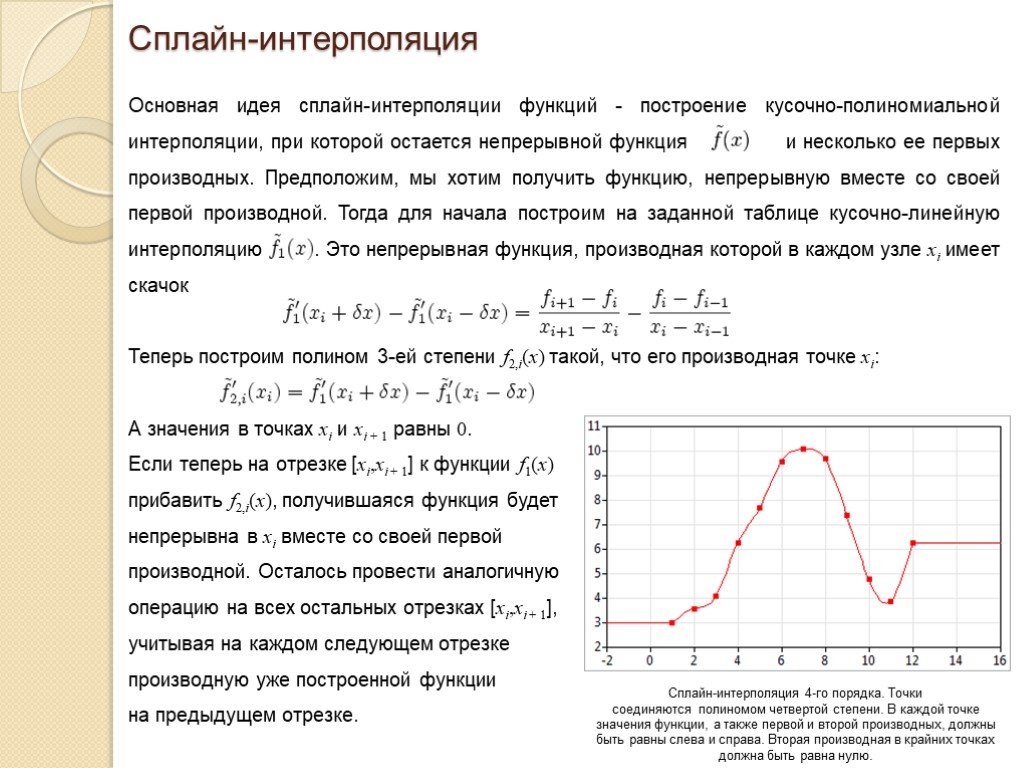
Слайд 15Сплайн-интерполяция Основная идея сплайн-интерполяции функций - построение кусочно-полиномиальной интерполяции, при которой остается непрерывной функция и несколько ее первых производных. Предположим, мы хотим получить функцию, непрерывную вместе со своей первой производной. Тогда для начала построим на заданной таблице кусочно-линейную интерполяцию . Это непрерывная функция, производная которой в каждом узле xi имеет скачок Теперь построим полином 3-ей степени f2,i(x) такой, что его производная точке xi: А значения в точках xi и xi + 1 равны 0. Если теперь на отрезке [xi,xi + 1] к функции f1(x) прибавить f2,i(x), получившаяся функция будет непрерывна в xi вместе со своей первой производной. Осталось провести аналогичную операцию на всех остальных отрезках [xi,xi + 1], учитывая на каждом следующем отрезке производную уже построенной функции на предыдущем отрезке.
Сплайн-интерполяция 4-го порядка. Точки соединяются полиномом четвертой степени. В каждой точке значения функции, а также первой и второй производных, должны быть равны слева и справа. Вторая производная в крайних точках должна быть равна нулю.

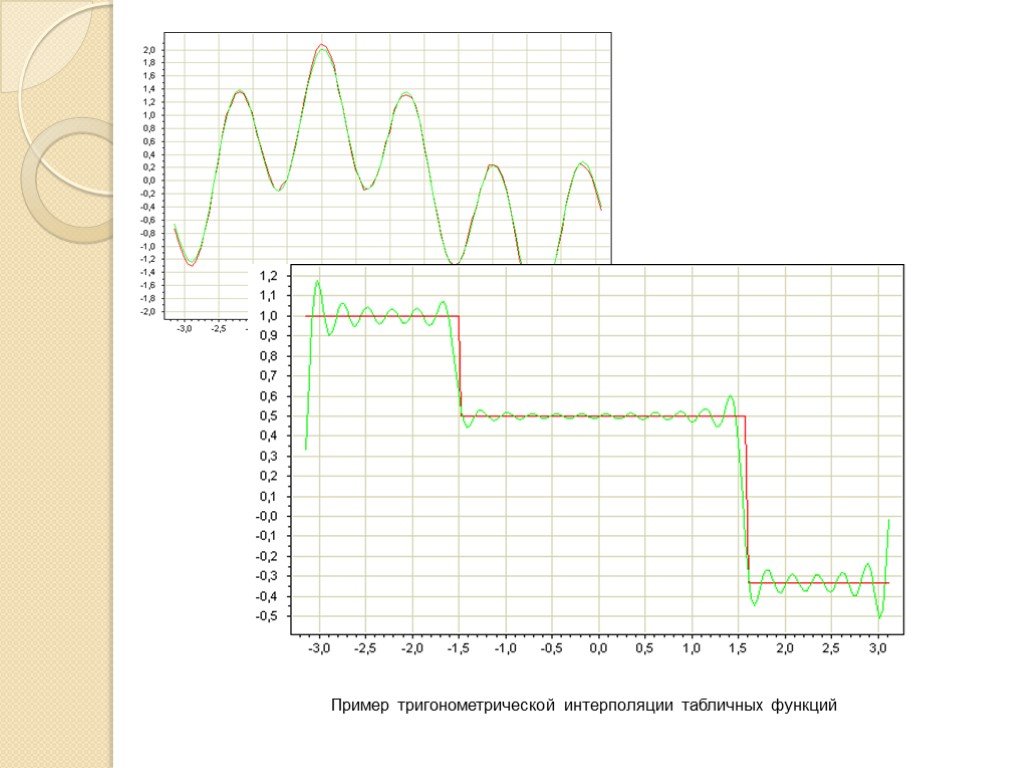
Слайд 16Тригонометрическая интерполяция Другим важным видом интерполяции является интерполяция функции f(x) тригонометрическим полиномом, называемой еще интерполяцией полиномом Фурье: Интерполирующая функция представляет собой сумму конечного числа гармоник ряда Фурье. Этот вид интерполяции особенно подходит для периодических функций. Пусть есть функция f(x) с периодом L, т.е. для любого x: f(x + L) = f(x) Пусть эта функция задана таблицей на периодической сетке: своими значениями fn = f(xn). Оказывается, при правильном выборе N,K,x0, существует только один полином .
Слайд 17Пример тригонометрической интерполяции табличных функций
Слайд 18Неклассические методы интерполяции
В различных приложениях используются различные методы интерполяции, не сводящиеся к классическим. Рассмотрим некоторые из них. Реконструкция функций Для реконструкции разрывных функций часто применяют так называемую minmod-реконструкцию. Суть ее в следующем: Распределение функции на отрезке полагается линейным, а коэффициент наклона выбирается как где

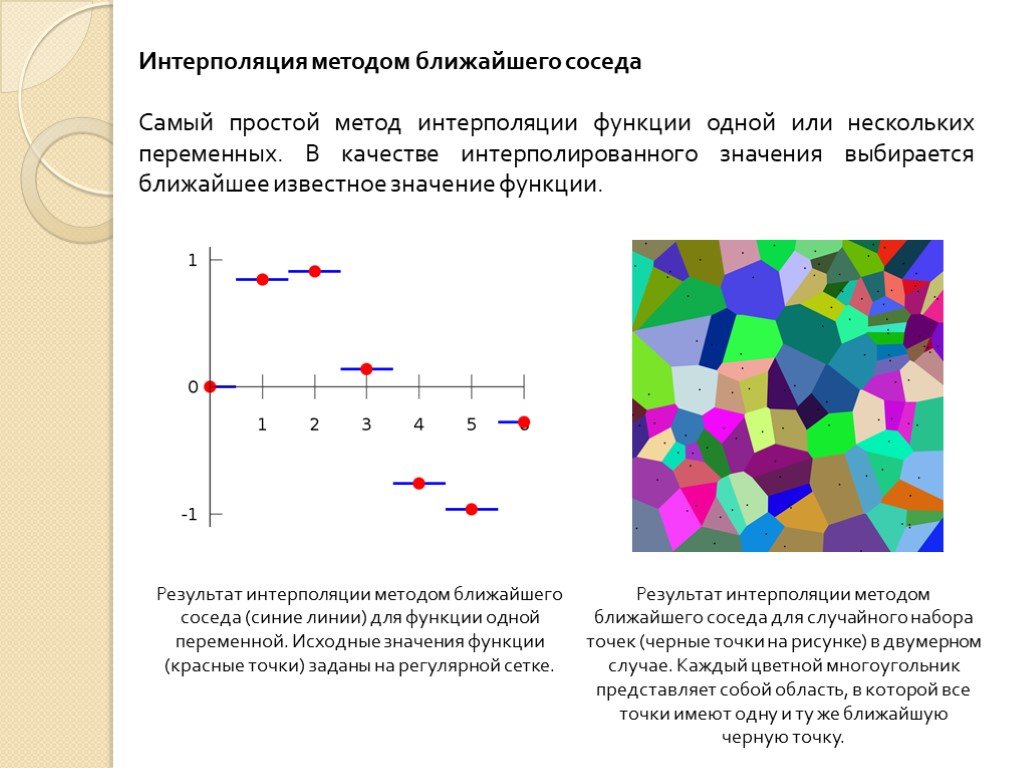
Слайд 19Интерполяция методом ближайшего соседа Самый простой метод интерполяции функции одной или нескольких переменных. В качестве интерполированного значения выбирается ближайшее известное значение функции.
Результат интерполяции методом ближайшего соседа (синие линии) для функции одной переменной. Исходные значения функции (красные точки) заданы на регулярной сетке.
Результат интерполяции методом ближайшего соседа для случайного набора точек (черные точки на рисунке) в двумерном случае. Каждый цветной многоугольник представляет собой область, в которой все точки имеют одну и ту же ближайшую черную точку.
Слайд 202D интерполяция Билинейная интерполяция Бикубическая интерполяция Интерполяция методом ближайшего соседа
Слайд 21Экстраполяция
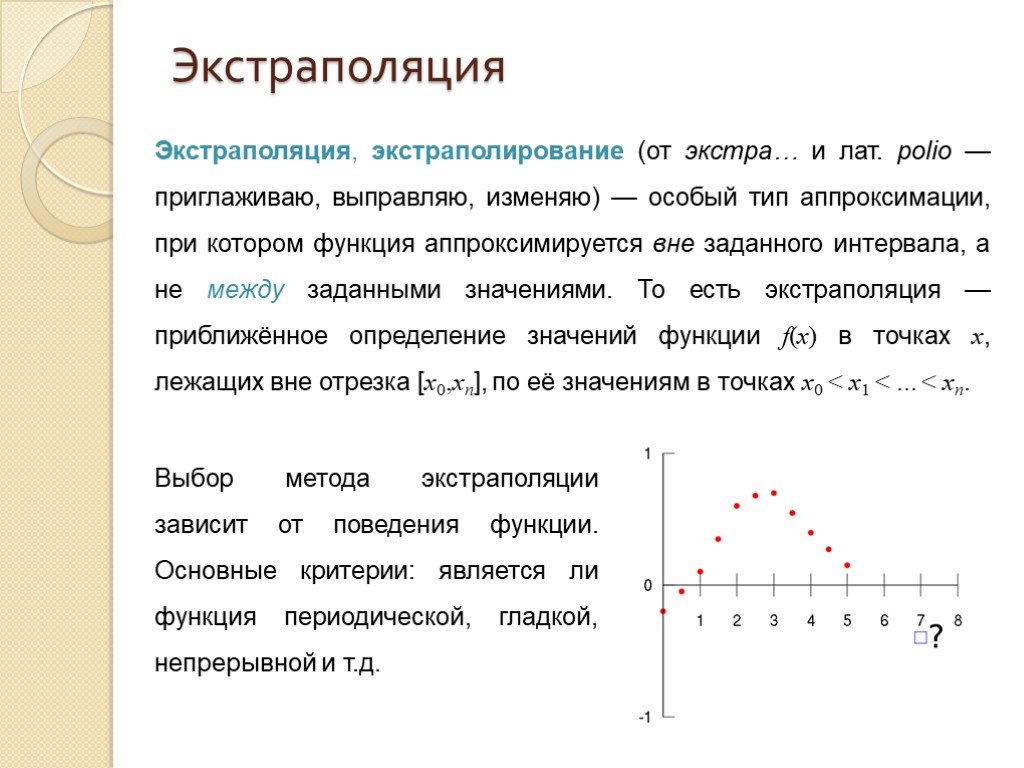
Экстраполяция, экстраполирование (от экстра… и лат. polio — приглаживаю, выправляю, изменяю) — особый тип аппроксимации, при котором функция аппроксимируется вне заданного интервала, а не между заданными значениями. То есть экстраполяция — приближённое определение значений функции f(x) в точках x, лежащих вне отрезка [x0,xn], по её значениям в точках x0 < x1 < ... < xn.
Выбор метода экстраполяции зависит от поведения функции. Основные критерии: является ли функция периодической, гладкой, непрерывной и т.д.
Слайд 22Экстраполяция - метод научного прогнозирования, состоящий в распространении выводов, получаемых из наблюдения над одной частью явления на другую его часть.
Слайд 23Линейная экстраполяция Линейная экстраполяция позволяет построить тангенциальную линию на конце набора табличных данных, по которой может быть оценены значения, находящиеся за ней. Линейная экстраполяция дает неплохие результаты только в случае когда использует данные квазилинейной функции и в области не далеко отстоящей от границы табличных данных. Если у нас есть две точки с координатами (xk − 1,yk − 1) и (xk, yk), линейная экстраполяция для точки x * будет определена следующей функцией:
(идентична линейной интерполяции в случае xk − 1 < x * < xk). Возможно также включение большего числа точек и усреднение наклона кривой по этим данным методом регрессии.

Слайд 24Polynomial extrapolation A polynomial curve can be created through the entire known data or just near the end. The resulting curve can then be extended beyond the end of the known data. Polynomial extrapolation is typically done by means of Lagrange interpolation or using Newton's method of finite differences to create a Newton series that fits the data. The resulting polynomial may be used to extrapolate the data. High-order polynomial extrapolation must be used with due care. For the example data set and problem in the figure above, anything above order 1 (linear extrapolation) will possibly yield unusable values, an error estimate of the extrapolated value will grow with the degree of the polynomial extrapolation. This is related to Runge's phenomenon. Conic extrapolation A conic section can be created using five points near the end of the known data. If the conic section created is an ellipse or circle, it will loop back and rejoin itself. A parabolic or hyperbolic curve will not rejoin itself, but may curve back relative to the X-axis. This type of extrapolation could be done with a conic sections template (on paper) or with a computer. French curve extrapolation French curve extrapolation is a method suitable for any distribution that has a tendency to be exponential, but with accelerating or decelerating factors. This method has been used successfully in providing forecast projections of the growth of HIV/AIDS in the UK since 1987 and variant CJD in the UK for a number of years.

Слайд 25Задание на практику
Реализовать программно Интерполяционный полином Лагранжа для произвольной табличной функции Построить узловые точки функции/функцию на экране Указать графически: - интерполяционную кривую - график ошибки интерполяции



























![Погрешность интерполирования Пусть интерполяционный многочлен Лагранжа построен для известной функции f(x). Необходимо выяснить, насколько этот многочлен близок к функции в точках отрезка [a, b], отличных от узлов. Погрешность интерполяции равна |f(x) – Ln(x)|. Оценку погрешности можно получить на о Погрешность интерполирования Пусть интерполяционный многочлен Лагранжа построен для известной функции f(x). Необходимо выяснить, насколько этот многочлен близок к функции в точках отрезка [a, b], отличных от узлов. Погрешность интерполяции равна |f(x) – Ln(x)|. Оценку погрешности можно получить на о](https://prezentacii.org/upload/cloud/19/06/153432/images/thumbs/screen11.jpg)