Презентация "Задачи оптимизации" – проект, доклад

Задачи оптимизации

Преподаватель Трофимова Виолетта Шамильевна к.э.н., доцент кафедры Математических методов в экономике МГТУ им. Носова

Исследование операций

Исследование операций — научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее эффективного управления различными организационными системами. Цель исследования операций — количественное обоснование принимаемых решений по организации управления. При решении задачи управления применение методов исследования операций предполагает: построение экономических и математических моделей для задач принятия решения в сложных ситуациях или в условиях неопределенности; изучение взаимосвязей, определяющих впоследствии принятие решений, и установление критериев эффективности, позволяющих оценивать преимущество того или иного варианта действия.

Примеры задач исследования операций

Задача 1. Для обеспечения высокого качества выпускаемых изделий на заводе организуется система выборочного контроля. Требуется выбрать такие формы его организации — например, назначить размеры контрольных партий, указать последовательность контрольных операций, определить правила отбраковки, — чтобы обеспечить необходимое качество при минимальных расходах. Задача 2. Для реализации определенной партии сезонных товаров создается сеть временных торговых точек. Требуется выбрать параметры сети — число точек, их размещение, количество персонала — так, чтобы обеспечить максимальную экономическую эффективность распродажи. Задача 3. Металлургический комбинат имеет 4 доменных печи. Производимый ими чугун транспортируется в 4 сталеплавильных цеха. Известны значения расходных коэффициентов чугуна, показывающих, сколько тонн чугуна из каждой доменной печи расходуется на производство одной тоны стали в каждом сталеплавильном цехе. Определить сколько нужно производить стали в каждом цехе и из чугуна какой доменной печи, так, чтобы прибыль от производства была максимальной.

Основные понятия

Операция - любое управляемое мероприятие, направленное на достижение цели. Результат операции зависит от способа её проведения и организации, т.е. выбора определенных параметров. Всякий определенный выбор параметров называется решением. Оптимальным решением считают те, которые по тем или иным соображениям лучше других.

Модель операции — это достаточно точное описание операции с помощью математического аппарата (различного рода функций, уравнений, систем уравнений и неравенств и т.п.) Эффективность операции - степень ее приспособленность к выполнению задачи - количественно выражается в виде критерия эффективности - целевой функции. Z = f(x1,x2,…,α1,α2,…) αj – постоянные факторы (условия проведения операции) xi – зависимые факторы (элементы решения)

Классификация моделей исследования операций

Все модели исследования операций могут быть классифицированы в зависимости от природы и свойств операции, характера решаемых задач, особенностей применяемых математических методов. Классы задач: Оптимизационные задачи Задачи сетевого планирования и управления Задачи массового обслуживания Задачи управления запасами Задачи распределения ресурсов Задачи ремонта и замены оборудования Задачи составления расписания (календарного планирования) Задачи планировки и размещения Задачи выбора маршрута, или сетевые задачи Задачи принятия оптимальных решений в конфликтных ситуациях (игровые модели) Многокритериальные задачи исследования операции и т.д.

Оптимизационные задачи

Общая постановка задачи оптимизации: Найти переменные x1,x2,…, xn которые удовлетворяют системе неравенств (уравнений) φi (x1,x2,…,xn) ≤ bi , i=1,…,m и обращающие в максимум (или минимум) целевую функцию Z = f(x1,x2,…,xn) →max (min) Решением является точка n-мерного пространства

Классификация методов решения задач оптимизации

классические методы оптимизации методы математического программирования линейного целочисленного линейного нелинейного выпуклого динамического геометрического параметрического стохастического эвристического программирования

Основоположники исследования операций

российские ученые: Л. В. Канторович, Н.П. Бусленко, Е.С. Вентцель, Н.Н. Воробьев, Н.Н. Моисеев, Д.Б. Юдин и многие другие зарубежные ученые: Р. Акоф, Р. Беллман, Г. Данциг, Г. Кун, Дж. Нейман, Т. Саати, Р. Черчмен, А. Кофман и др.

Леонид Витальевич Канторович (6 (19) января 1912, Санкт-Петербург — 7 апреля 1986, Москва) — советский математик и экономист, лауреат Нобелевской премии по экономике 1975 года (с Т. Купманс (1910-1985, родился в Нидерландах, работал в основном в США) «за вклад в теорию оптимального распределения ресурсов». Пионер и один из создателей линейного программирования.

Линейное программирование

Линейное программирование – область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума или минимума) линейной функции многих переменных при наличии линейных ограничений, т.е. линейных равенств или неравенств, связывающих эти переменные. Общая постановка задачи линейного программирования Найти значения переменных x1, x2,…,xn, максимизирующие линейную форму

при условиях:

Постановка задачи линейного программирования

Целевая функция: c1 Х1 + с2 Х2 +…+сn Xn→ max , Ограничения: a11 Х1 + a12 Х2 +…+a1n Xn ≤ b1 , a21 Х1 + a22 Х2 +…+a2n Xn ≤ b2 , …. ak 1 Х1 + ak 2 Х2 +…+ak n Xn ≤ bk , k ≤m ak+1 1 Х1 + ak+1 2 Х2 +…+ak+1 n Xn = bk+1 , ….. am 1 Х1 + am 2 Х2 +…+am n Xn = bm , Условие неотрицательности: Х1 ≥ 0 , Х2 ≥ 0,…, Хh ≥ 0 , h ≤ n . Искомые переменные: Х1, Х2,…, Хn

Примеры задач линейного программирования: планирование производства или использования ресурсов

Задача 1 Цех может производить стулья и столы. На производство стула идет 5 единиц материала, на производство стола - 20 единиц (футов красного дерева). Стул требует 10 человеко-часов, стол - 15. Имеется 400 единиц материала и 450 человеко-часов. Прибыль при производстве стула - 45 долларов США, при производстве стола - 80 долларов США. Сколько надо сделать стульев и столов, чтобы получить максимальную прибыль? Математическая модель задачи имеет вид: Обозначим: Х1 - число изготовленных стульев, Х2 - число сделанных столов. Целевая функция: 45 Х1 + 80 Х2 → max , Ограничения: 5 Х1 + 20 Х2 ≤ 400 , 10 Х1 + 15 Х2 ≤ 450 , Х1 ≥ 0 , Х2 ≥ 0 и целые.

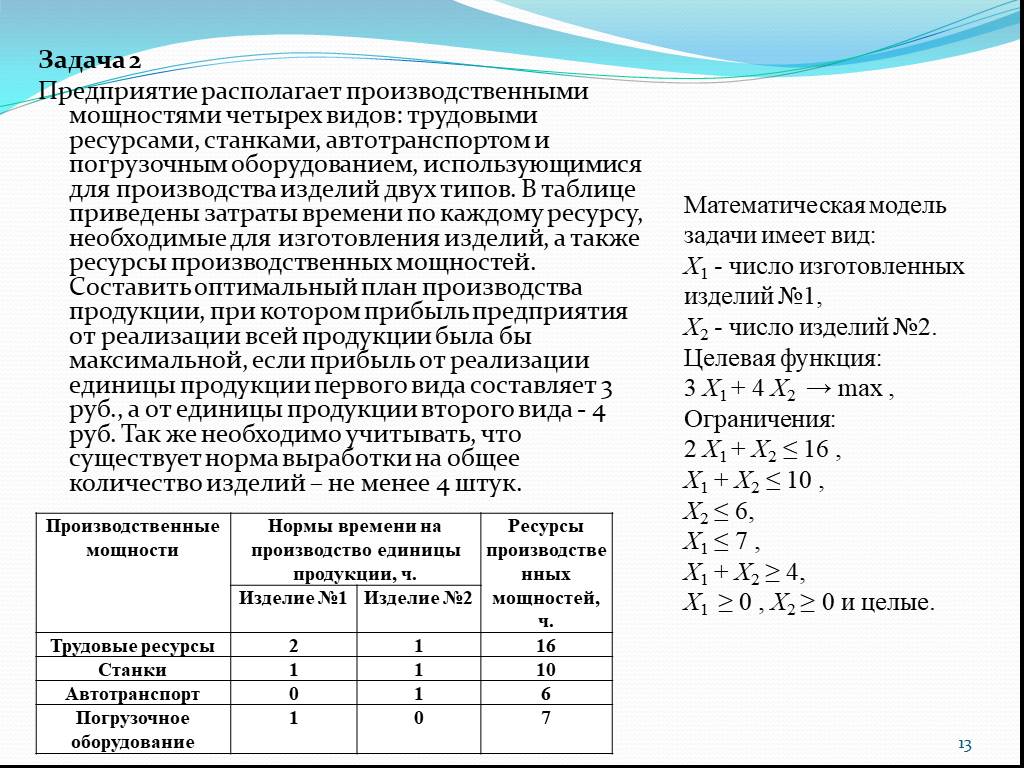
Задача 2 Предприятие располагает производственными мощностями четырех видов: трудовыми ресурсами, станками, автотранспортом и погрузочным оборудованием, использующимися для производства изделий двух типов. В таблице приведены затраты времени по каждому ресурсу, необходимые для изготовления изделий, а также ресурсы производственных мощностей. Составить оптимальный план производства продукции, при котором прибыль предприятия от реализации всей продукции была бы максимальной, если прибыль от реализации единицы продукции первого вида составляет 3 руб., а от единицы продукции второго вида - 4 руб. Так же необходимо учитывать, что существует норма выработки на общее количество изделий – не менее 4 штук.

Математическая модель задачи имеет вид: Х1 - число изготовленных изделий №1, Х2 - число изделий №2. Целевая функция: 3 Х1 + 4 Х2 → max , Ограничения: 2 Х1 + Х2 ≤ 16 , Х1 + Х2 ≤ 10 , Х2 ≤ 6, Х1 ≤ 7 , Х1 + Х2 ≥ 4, Х1 ≥ 0 , Х2 ≥ 0 и целые.

Задача 3 В отделе технического контроля (ОТК) некоторой фирмы работают контролеры разрядов 1 и 2. Норма выработки ОТК за восьмичасовой рабочий день составляет не менее 1800 изделий. Контролер 1 разряда проверяет 25 изделий в час, причем не ошибается в 98% случаев. Контролер 2 разряда проверяет 15 изделий в час, и его точность составляет 95%. Заработная плата контролера 1 разряда равна 4 $ в час, контролер 2 разряда получает 3 $ в час. При каждой ошибке контролера фирма несет убыток в размере 2 долл. Фирма может нанять максимум 8 контролеров 1 разряда и 10 контролеров 2 разряда. Определить оптимальный состав ОТК, при котором общие расходы фирмы на контроль будут минимальными.

Математическая модель задачи имеет вид: Обозначим: Х1 - число контролеров 1 разряда, Х2 - контролеров 2 разряда Целевая функция (общие затраты на оплату труда контролеров в час): 4Х1 + 3 Х2 + 2(25∙0,02 ∙ Х1 + 15∙0,05 ∙ Х2)→ min , Ограничения: 8 ∙(25 Х1 + 15 Х2 ) ≥ 1800 , Х1 ≤ 8 , Х2 ≤ 10 , Х1 ≥ 0 , Х2 ≥ 0 и целые.

Задача 4 Из двух сортов бензина составляют для различных целей две смеси А и В. Смесь А содержит 60% бензина первого и 40% бензина второго сорта, смесь В - 80% бензина первого и 20% бензина второго сорта. Составить оптимальный план образования смесей, при котором будет получен максимальный доход, если имеется 50000 л бензина первого и 30000 л второго сорта. и продажная цена 1 л смеси А составляет 10 руб., а смеси В - 12 руб. При этом, смеси А должно быть не менее, чем в 2 раза больше, чем смеси В.

Примеры задач линейного программирования: задача составления смесей или задача о диете

Математическая модель задачи имеет вид: Обозначим: Х1 – количество смеси А, Х2 - количество смеси В (тыс. литров) Целевая функция (доход от реализации смесей) в тыс. руб.: 10Х1 + 12 Х2 → max , Ограничения: 0,6Х1 + 0,8 Х2 ≤ 50 , 0,4Х1 + 0,2 Х2 ≤ 30 , Х1 - 2 Х2 ≥ 0 Х1 ≥ 0 , Х2 ≥ 0.

Задача 5 (о диете) Предположим, что необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ (например, тиамина Т и ниацина Н).

Пищевая ценность рациона должна быть не менее 400 калорий. Смесь для цыплят изготавливается из двух продуктов. Известно содержание тиамина и ниацина в этих продуктах, а также питательная ценность. Сколько унций каждого продукта надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна?

Задача линейного программирования имеет вид: 3,8 Х1 + 4,2 Х2 → min , 0,10 Х1 + 0,25 Х2 ≥ 1,00 , 1,00 Х1 + 0,25 Х2 ≥ 5,00 , 110,00 Х1 + 120,00 Х2 ≥ 400,00 , Х1 ≥ 0 , Х2 ≥ 0 .

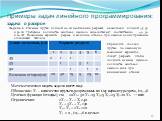
Задача 6 Стальные прутья длиной 110 см необходимо разрезать на заготовки длиной 45, 35 и 50 см. Требуемое количество заготовок данного вида составляет соответственно 40, 30 и 20 шт. Возможные варианты разреза и величина отходов при каждом из них приведены в следующей таблице:

Примеры задач линейного программирования: задача о раскрое

Определить, сколько прутьев по каждому из возможных вариантов следует разрезать, чтобы получить не менее нужного количества заготовок каждого вида при минимальных отходах.

Математическая модель задачи имеет вид: Обозначим: Хi – количество прутьев, разрезанных по i-му варианту разреза, i=1,…,6 Целевая функция (отходы), см: 20Х1 + 30 Х2 +15 Х3+5 Х4+25 Х5 +10 Х6 → min Ограничения: 2Х1 + Х2 + Х3 ≥40 Х2 + 3Х4 + Х5 ≥30 Х3+ Х5 + 2Х6 ≥20 Хj ≥ 0 , j=1,…,6 и целые.

Задача 7 Для изготовления брусьев длиной 1,2 м, 3 м и 5 м в соотношении 2:1:3 на распил поступают 195 бревен длиной 6 м. Определить план распила, обеспечивающий максимальное число комплектов.

Математическая модель задачи имеет вид: Обозначим: Хi – количество бревен, разрезанных по i-му варианту разреза, i=1,2,3,4; x – количество комплектов; Целевая функция: x → max (максимизация кол-ва комплектов) или : 0,6 Х2 +Х4 → min (минимизация отходов) Ограничения: Х1 + Х2 + Х3 + Х4 = 195 5Х1 + 2Х2 =2x Х2+ 2Х3 =x Х4 =3x Хj ≥ 0 , j=1,2,3,4 и целые.

Методы решения задач линейного программирования

Графический метод (n=2) Симплексный метод (simplex (лат) – простой) Метод искусственного базиса (больших штрафов) Модифицированный симплекс-метод Метод потенциалов Венгерский метод Метод отсечения Метод Гомори Метод ветвей и границ и др.

Решение ЗЛП графическим способом

Задача 8. Условие: Фабрика выпускает пряжу двух видов: П1 и П2. Продукция поступает в оптовую продажу. Для производства используется три вида сырья – шерсть, капрон и акрил. Максимально возможные суточные запасы этих материалов составляют 6, 8 и 5 тонн соответственно. Расходы сырья на партию пряжи и оптовые цены приведены в таблице:

Изучение рынка сбыта показало, что суточный спрос на пряжу П2 никогда не превышает спроса на пряжу П1 более чем на одну партию. Кроме того, установлено, что спрос на пряжу П2 никогда не превышает 2 партий.

Вопрос: Какое количество пряжи (в партиях) каждого вида должна производить фабрика, что бы доход от реализации продукции был максимальным?

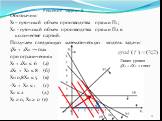
Обозначим: X1 – суточный объем производства пряжи П1; X2 - суточный объем производства пряжи П2 в количестве партий. Получаем следующую математическую модель задачи: 3Х1 + 2Х2 → max при ограничениях Х1 + 2Х2 ≤ 6 (а) 2Х1 + Х2 ≤ 8 (б) Х1+0,8Х2 ≤ 5 (в) -Х1 + Х2 ≤ 1 (г) Х2 ≤ 2 (д) Х1 ≥ 0, Х2 ≥ 0 (е)

Линия уровня 3Х1 + 2Х2 = const

Решение задачи 8

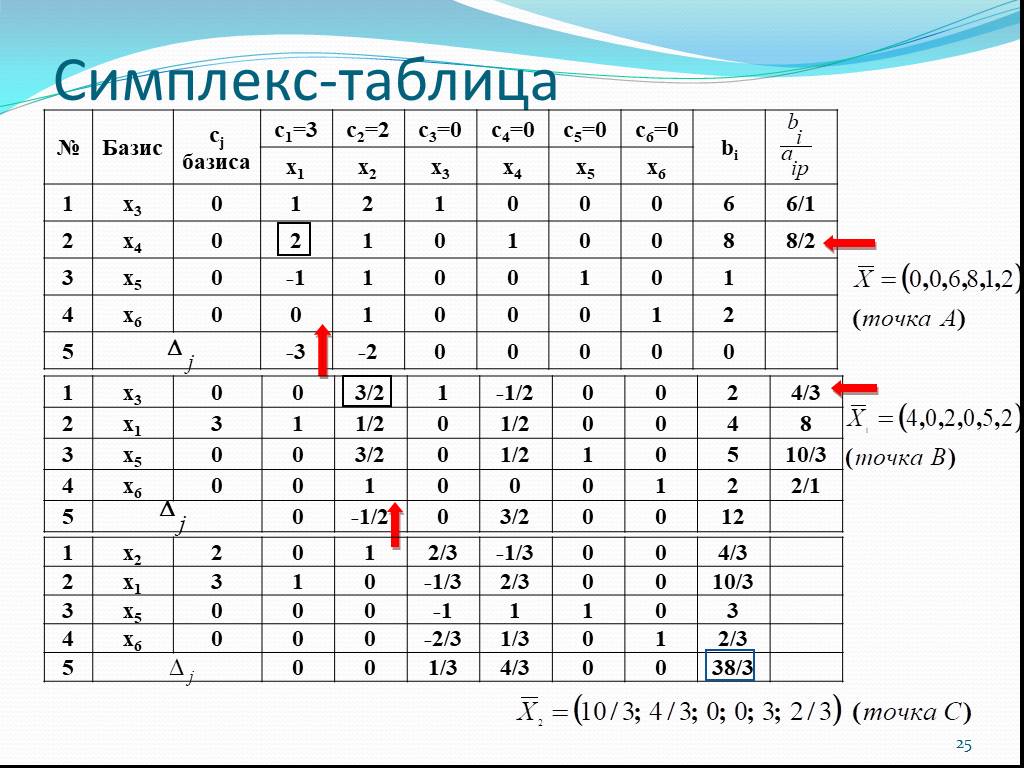
Угловая точка С – является точкой максимума , она лежит на пересечении прямых (а) и (б). Для определения ее координат решим систему уравнений: Х1 + 2Х2 = 6 2Х1 + Х2 = 8. Откуда Х*1 = 10/3; X*2 = 4/3 или = (10/3 ; 4/3). Подставляя значения Х*1 и X*2 в функцию , найдем max = = 3 . 10/3 + 2 . 4/3 = 38/3=12,67. Ответ: фабрике необходимо производить пряжи первого вида 3 и 1/3 партий, а второго вида – 1 и 1/3 партий. При этом фабрика получит максимальный доход от реализации всей пряжи 12,67 тыс. у.е.

Решение ЗЛП симплексным методом

Рассмотрим каноническую задачу линейного программирования (КЗЛП) Симплексные метод решения ЗЛП – это метод последовательного улучшения плана, который позволяет за конечное число шагов либо найти оптимальный план, либо установить его отсутствие. Симплексный метод состоит из трех основных этапов: Отыскание начального опорного плана. Переход от одного опорного плана к другому, значение целевой функции в котором больше, чем в предыдущем. Проверка оптимальности полученного плана, позволяющая своевременно остановить перебор опорных планов или сделать вывод об отсутствии оптимального плана.

Пример 8

Решить ЗЛП из примера 8 симплексным методом:

Приводим систему линейных неравенств к каноническому виду, вводя в каждое неравенство дополнительную неотрицательную переменную. Получим систему линейных уравнений:

Целевая функция будет иметь вид

Составляем симплекс – таблицу:

Симплекс-таблица

Производственное предприятие изготавливает два вида изделия А и В. Потребители продукции готовы приобрести за неделю 100 единиц продукции А по цене 3000 руб за единицу и 50 единиц продукции В по цене 3200 руб за единицу. Предприятие использует в производственном процессе 9 агрегатов. Структура технологических маршрутов предприятия с длительностью операций представлена на рисунке. Общий фонд времени работы каждого агрегата за неделю 2400 мин (5 дней по 8 часов). Для производства единицы изделия А используется два вида исходного сырья: «а» по 600 руб/ед и «б» по 400 руб/ед. Изделие В изготавливается из сырья «б» и «в» по 400 руб/ед. Необходимо определить максимальную прибыль, которую может получить предприятие за неделю, если объем постоянных расходов составляет 100 тыс. руб.

В.М. Салганик и др. Методология и алгоритмы методов теории ограничений для производственного планирования и менеджмента качества. – Магнитогорск: МГТУ, 2009

Задача 9

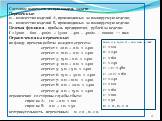
Составим математическую модель задачи: Переменные: x1 – количество изделий А, производимых за планируемую неделю; x2 - количество изделий В, производимых за планируемую неделю. Целевая функция – прибыль предприятия, рублей за неделю: f = (3000 - 600 – 400)x1 + (3200 – 400 – 400)x2 – 100000 → max Ограничения на переменные: по фонду времени работы каждого агрегата: агрегат 1: 20∙x1 + 0∙x2 ≤ 2400 агрегат 2: 10∙x1 + 0∙x2 ≤ 2400 агрегат 3: 15∙x1 + 0∙x2 ≤ 2400 агрегат 4: 10∙x1 + 0∙x2 ≤ 2400 агрегат 5: 5∙x1 + 5∙x2 ≤ 2400 агрегат 6: 15∙x1 + 30∙x2 ≤ 2400 агрегат 7: 0∙x1 + 10∙x2 ≤ 2400 агрегат 8: 0∙x1 + 20∙x2 ≤ 2400 агрегат 9: 0∙x1 + 15∙x2 ≤ 2400 ограничения со стороны службы сбыта: спрос на А: 1∙x1 + 0∙x2 ≤ 100 спрос на В: 0∙x1 + 1∙x2 ≤ 50 неотрицательность переменных: x1 ≥ 0 , x2 ≥ 0.

2000 x1 + 2400 x2 – 100 000 → max x1 ≤ 120 x1 ≤ 240 x1 ≤ 160 x1 ≤ 240 x1 + x2 ≤ 480 x1 +2 x2 ≤ 160 x2 ≤ 240 x2 ≤ 120 x2 ≤ 160 x1 ≤ 100 x2 ≤ 50 x1 ≥ 0 , x2 ≥ 0

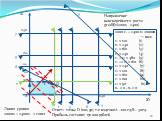
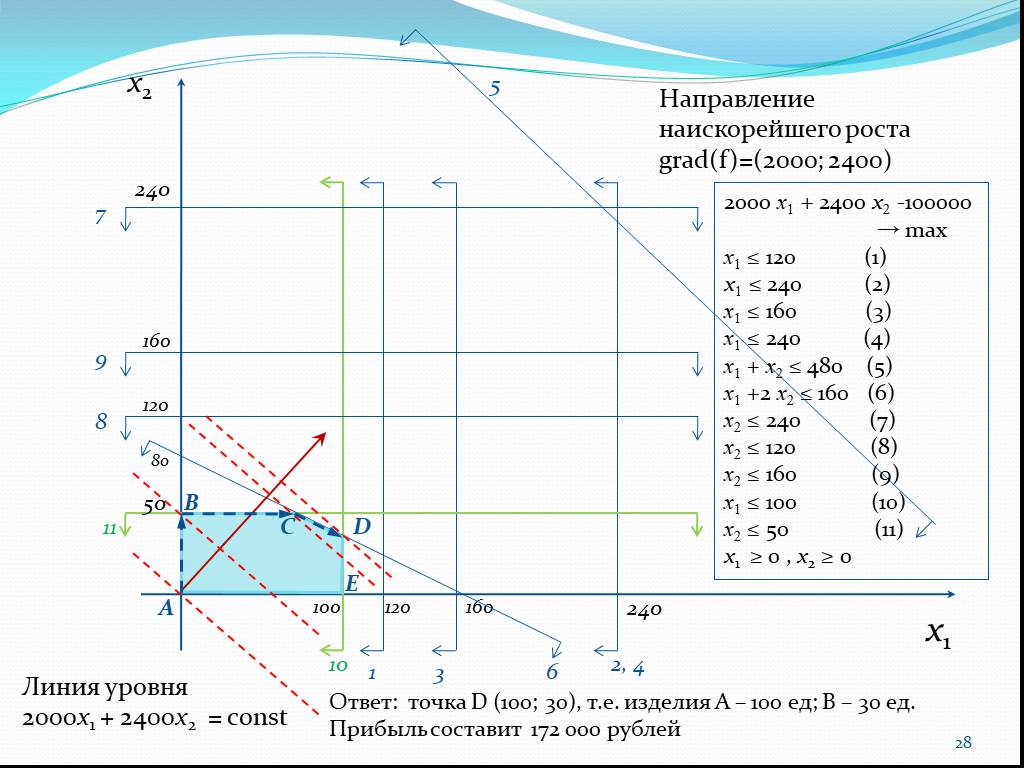
x1 x2 100 160 120 240 50 10 3 1 2, 4 5 11 8 9 7 80 6 А С В D

Линия уровня 2000x1 + 2400x2 = const

Направление наискорейшего роста grad(f)=(2000; 2400)

E

2000 x1 + 2400 x2 -100000 → max x1 ≤ 120 (1) x1 ≤ 240 (2) x1 ≤ 160 (3) x1 ≤ 240 (4) x1 + x2 ≤ 480 (5) x1 +2 x2 ≤ 160 (6) x2 ≤ 240 (7) x2 ≤ 120 (8) x2 ≤ 160 (9) x1 ≤ 100 (10) x2 ≤ 50 (11) x1 ≥ 0 , x2 ≥ 0

Ответ: точка D (100; 30), т.е. изделия А – 100 ед; В – 30 ед. Прибыль составит 172 000 рублей

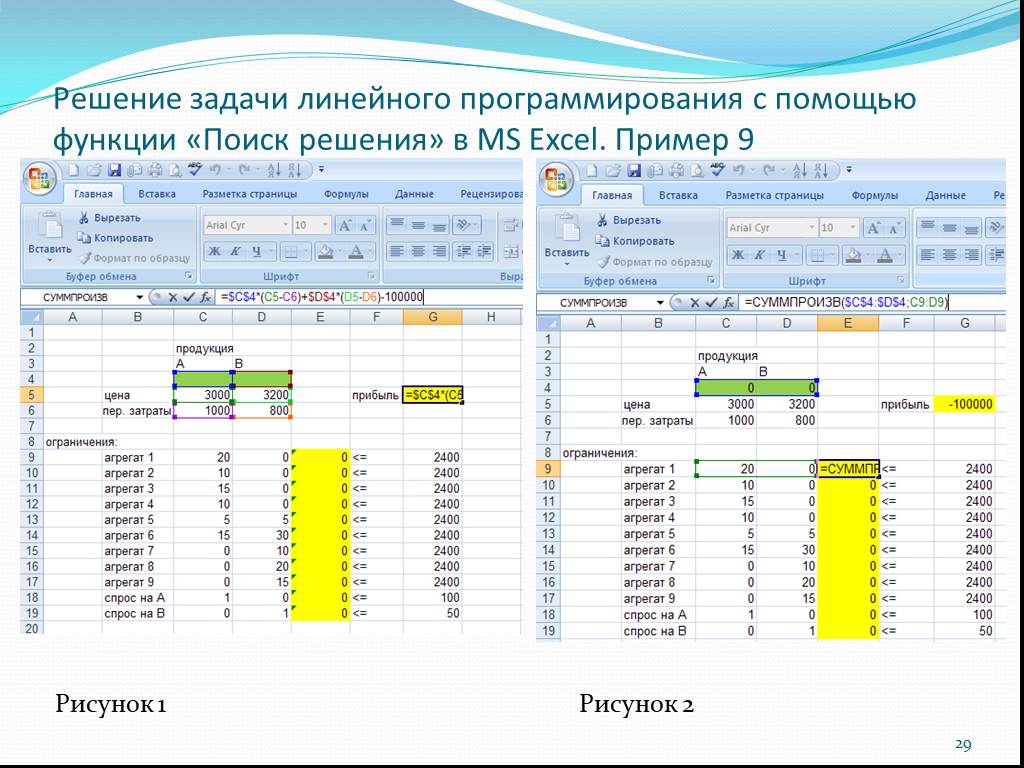
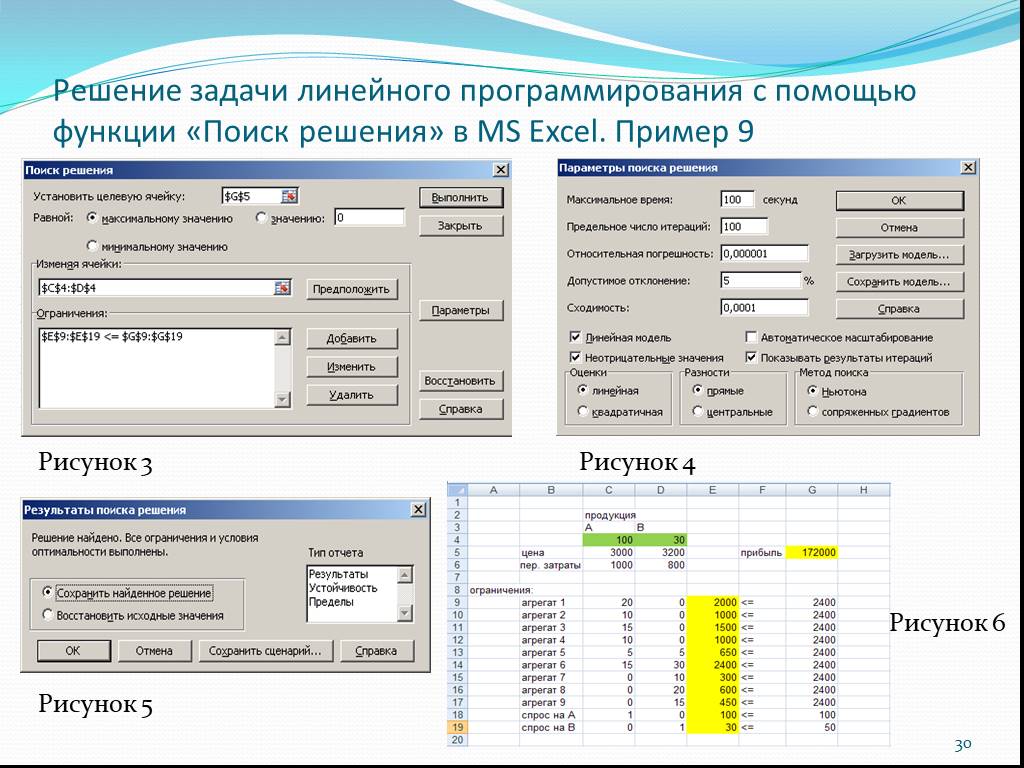
Решение задачи линейного программирования с помощью функции «Поиск решения» в MS Excel. Пример 9

Рисунок 1 Рисунок 2

Рисунок 3 Рисунок 4 Рисунок 5 Рисунок 6

Экономический анализ задачи ЛП с использованием теории двойственности

Для каждой задачи линейного программирования по определенным правилам можно поставить двойственную задачу. Переменными двойственной задачи будут двойственные оценки ресурсов (теневые, неявные, учетные, объективно обусловленные цены ресурсов). Результаты решения двойственной задачи можно увидеть при решении ЗЛП в MS Excel, если заказать отчет по результатам и отчет по устойчивости (они выводятся на отдельные листы)

Таблица 1

Для симметричных двойственных задач (как в таблице 1) двойственная задача строится по следующим правилам: Каждому неравенству системы ограничений исходной задачи ставим в соответствие переменную yi. Составляем целевую функцию, коэффициентами которой являются свободные члены системы ограничений исходной задачи. Если исходная задача на максимум, то двойственная – на минимум. Составляем систему ограничений. Коэффициенты системы ограничений образуют транспонированную матрицу коэффициентов системы ограничений исходной задачи. Знаки неравенств меняются на противоположные. Свободными членами системы ограничений являются коэффициенты целевой функции исходной задачи. Все переменные двойственной задачи неотрицательные.

Пример 10 составления двойственной задачи

Исходная задача

Двойственная задача

Решение двойственной задачи

При решении исходной задачи решение двойственной задачи находится автоматически, используя 1 и 2-ую теоремы двойственности (см лит-ру). При этом наблюдается взаимно однозначное соответствие переменных:

Двойственная задача для примера 9

2000 x1 + 2400 x2 -100000 → max x1 ≤ 120 |y1 x1 ≤ 240 |y2 x1 ≤ 160 |y3 x1 ≤ 240 |y4 x1 + x2 ≤ 480 |y5 x1 +2 x2 ≤ 160 |y6 x2 ≤ 240 |y7 x2 ≤ 120 |y8 x2 ≤ 160 |y9 x1 ≤ 100 |y10 x2 ≤ 50 |y11 x1 ≥ 0 , x2 ≥ 0

T

120 y1 +240 y2 +160 y3 +240 y4+480 y5 +160 y6 + 240 y7 + 120 y8 +160 y9+ 100 y10 + 50 y11 → min y1 + y2 +y3 + y4+ y5 + y6 +y10 ≥ 2000 y5 + 2 y6 +y7 + y8+ y9 + 2 y10 +y11 ≥ 2400 yi ≥ 0 , i=1,…,11

Решение двойственной задачи в MS Excel Пример 9

После того, как запущена работа надстройки Поиск решения, в окне Результаты поиска решения предложат заказать 3 типа отчета. Щёлкните по первым двум: Результаты и Устойчивость. Эти отчеты появятся на отдельных листах Вашей книги в MS Excel.

Отчет по результатам

В верхней таблице выводиться исходное значение целевой функции и конечное (результат), которое достигается при оптимальном плане. В средней таблице – значения изменяемых ячеек в начале (исходное значение) и в конце (результат) – оптимальный план. В нижней таблице значения левых частей системы ограничений (столбец «Значение»), разница с правыми частями системы ограничений (столбец «Разница») и статус ограничения: «связное» или «не связное», т.е. указываются соответственно дефицитные и недефицитные виды ресурсов, на которые наложены ограничения задачи.

В столбце «Разница» указываются неиспользованные запасы ресурсов. Например, агрегат 1 будет простаивать 400 минут (6 часов 40 минут) в неделю; спрос на изделие В не будет удовлетворен на 20 единиц.

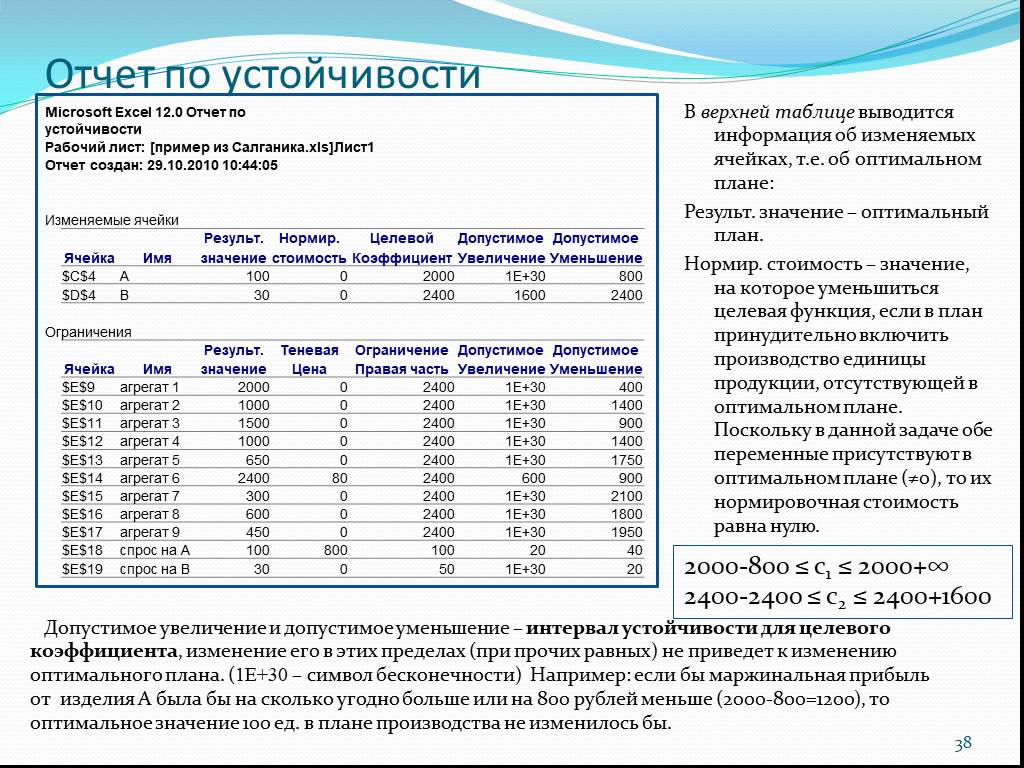
Отчет по устойчивости

В верхней таблице выводится информация об изменяемых ячейках, т.е. об оптимальном плане: Результ. значение – оптимальный план. Нормир. стоимость – значение, на которое уменьшиться целевая функция, если в план принудительно включить производство единицы продукции, отсутствующей в оптимальном плане. Поскольку в данной задаче обе переменные присутствуют в оптимальном плане (≠0), то их нормировочная стоимость равна нулю.

Допустимое увеличение и допустимое уменьшение – интервал устойчивости для целевого коэффициента, изменение его в этих пределах (при прочих равных) не приведет к изменению оптимального плана. (1Е+30 – символ бесконечности) Например: если бы маржинальная прибыль от изделия А была бы на сколько угодно больше или на 800 рублей меньше (2000-800=1200), то оптимальное значение 100 ед. в плане производства не изменилось бы.

2000-800 ≤ с1 ≤ 2000+∞ 2400-2400 ≤ с2 ≤ 2400+1600

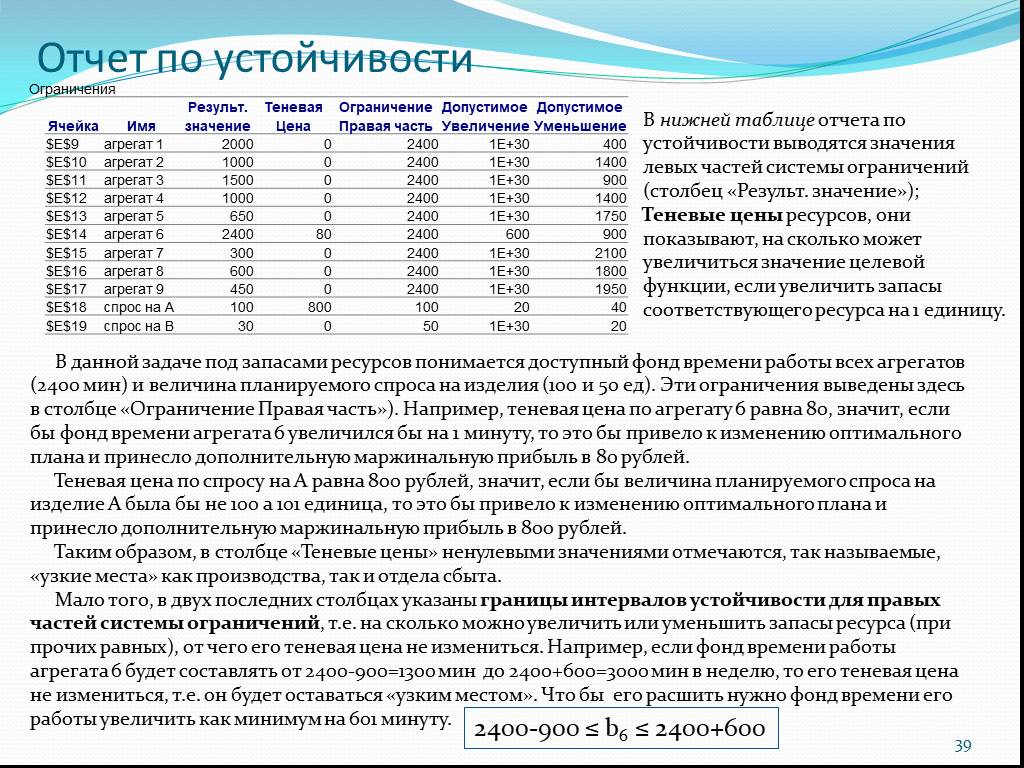
В нижней таблице отчета по устойчивости выводятся значения левых частей системы ограничений (столбец «Результ. значение»); Теневые цены ресурсов, они показывают, на сколько может увеличиться значение целевой функции, если увеличить запасы соответствующего ресурса на 1 единицу.

В данной задаче под запасами ресурсов понимается доступный фонд времени работы всех агрегатов (2400 мин) и величина планируемого спроса на изделия (100 и 50 ед). Эти ограничения выведены здесь в столбце «Ограничение Правая часть»). Например, теневая цена по агрегату 6 равна 80, значит, если бы фонд времени агрегата 6 увеличился бы на 1 минуту, то это бы привело к изменению оптимального плана и принесло дополнительную маржинальную прибыль в 80 рублей. Теневая цена по спросу на А равна 800 рублей, значит, если бы величина планируемого спроса на изделие А была бы не 100 а 101 единица, то это бы привело к изменению оптимального плана и принесло дополнительную маржинальную прибыль в 800 рублей. Таким образом, в столбце «Теневые цены» ненулевыми значениями отмечаются, так называемые, «узкие места» как производства, так и отдела сбыта. Мало того, в двух последних столбцах указаны границы интервалов устойчивости для правых частей системы ограничений, т.е. на сколько можно увеличить или уменьшить запасы ресурса (при прочих равных), от чего его теневая цена не измениться. Например, если фонд времени работы агрегата 6 будет составлять от 2400-900=1300 мин до 2400+600=3000 мин в неделю, то его теневая цена не измениться, т.е. он будет оставаться «узким местом». Что бы его расшить нужно фонд времени его работы увеличить как минимум на 601 минуту.

2400-900 ≤ b6 ≤ 2400+600

Специальные задачи линейного программирования

Транспортная задача Задача о назначениях Задача коммивояжера Задача календарного и оперативного планирования и др.

Постановка транспортной задачи (ТЗ)

Поставщики Количество А1 a1 А2 а2 … Am аm

Потребители Количество В1 b1 В2 b2 … Вn bn

ГРУЗ

Известна стоимость сij перевозки единицы груза от i-го поставщика к j-му потребителю. Необходимо составить самый дешевый план перевозок, позволяющий вывести все грузы у поставщиков и полностью удовлетворить потребителей.

Математическая модель ТЗ

Обозначим через хij количество единиц груза, запланированных к перевозке от i-го поставщика к j-му потребителю. Систему ограничений получаем из следующих условий задачи: а) все грузы должны быть перевезены, т.е. б) все потребности должны быть удовлетворены, т.е. Целевая функция - стоимость всех перевозок: → min

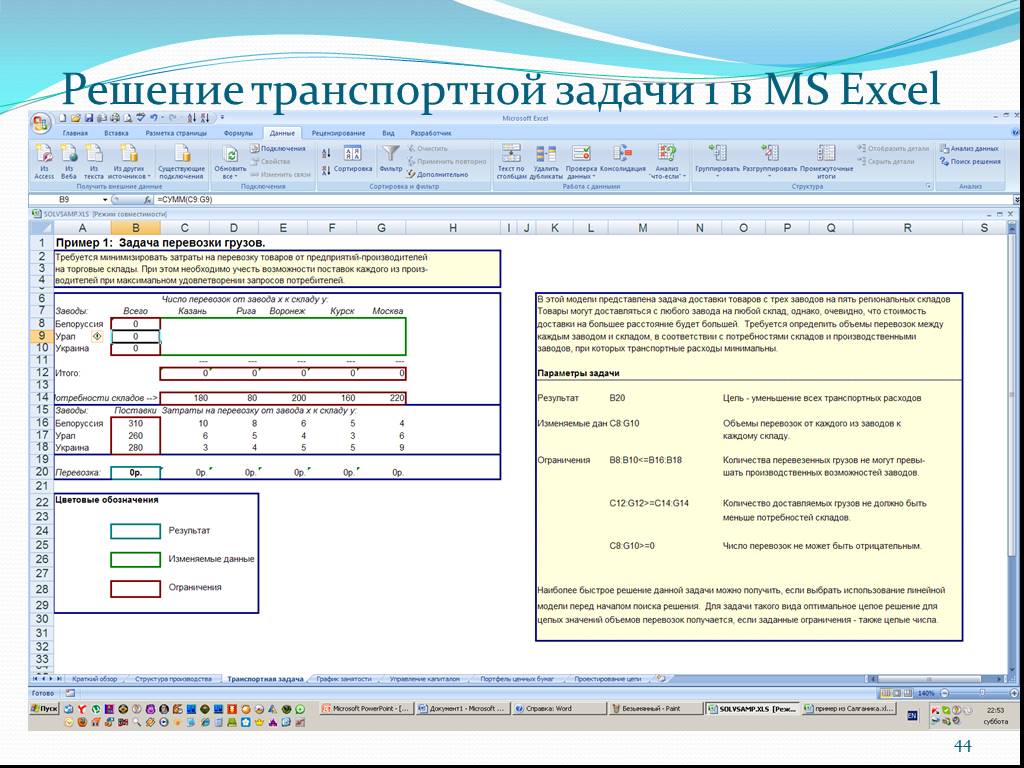
Требуется минимизировать затраты на перевозку товаров от трех предприятий-производителей на пять региональных торговых складов. При этом необходимо учесть возможности поставок каждого из производителей при максимальном удовлетворении запросов потребителей. Товары могут доставляться с любого завода на любой склад, однако, очевидно, что стоимость доставки на большее расстояние будет большей. Требуется определить объемы перевозок между каждым заводом и складом, в соответствии с потребностями складов и производством заводов, при которых транспортные расходы будут минимальны.

Пример транспортной задачи 1

Решение транспортной задачи 1 в MS Excel

Решение транспортной задачи 1

Общий расход на перевозку всех грузов составит 3200 р.

Пример транспортной задачи 2

Металлургический комбинат имеет четыре доменных печи, выпускающих соответственно 3020, 3220, 2920, 3020 т чугуна в сутки. Чугун транспортируется в четыре сталеплавильных цеха - кислородно-конвертерный (ККЦ), два мартеновских Цеха (МЦ1 и МЦ2) и в электросталеплавильный цех (ЭСПЦ). Известны расходные коэффициенты чугуна на производство одной тонны стали определяющие, сколько чугуна необходимо использовать для производства одной тонны стали. (приведены в таблице)

Известно, что в каждой доменной печи на конец суток остается переходящий запас чугуна в размере соответственно 200, 370, 340 и 320 т. Определить, сколько нужно производить стали в каждом цехе и из чугуна какой доменной печи, так, чтобы прибыль от производства была максимальной. Известно, что цена продажи тонны стали 1000 руб, а себестоимость выплавки 1 т стали в ККЦ составляет 378 руб., в мартеновском цехе 1 - 549 руб., в мартеновском цехе 2 - 552 руб. и в электросталеплавильном цехе - 555 руб.

Решение:

Обозначим: Хij – количество чугуна из i-й доменной печи, поставляемое в j-ый сталеплавильный цех, i=1,..,4; j=1,…,4; Найдем количество стали, произведенное в j-ом сталеплавильном цехе: ККЦ: Х11 /0,26 + Х21 /0,27 + Х31/0,29 +Х41 /0,36 = с1 МЦ1: Х12 /0,41 + Х22 /0,47 + Х32/0,41 +Х42 /0,42 = с2 МЦ2: Х13 /0,45 + Х23 /0,44 + Х33/0,39 +Х43 /0,44 = с3 ЭСПЦ: Х14 /0,46 + Х24 /0,46 + Х34/0,42 +Х44 /0,39 = с4 Целевая функция (прибыль от продажи стали) в руб.: 1000(с1 + с2 + с3+с4 ) - 378 с1 - 549 с2 - 552 с3 - 555 с4 → max Ограничения (по количеству чугуна, выпускаемого в доменных печах в сутки) : Х11 + Х12 + Х13 +Х14 = 3020 Х21 + Х22 + Х23 +Х24 = 3220 Х31 + Х32 + Х33 +Х34 = 2920 Х41 + Х42 + Х43 +Х44 = 3020 Хij ≥ 0 , i=1,..,4; j=1,…,4 Ответ: X= (решение найдено с помощью функции «Поиск решения» в MS Excel) То есть весь чугун следует направлять в ККЦ , который будет выпускать 41 999,16т стали; прибыль при этом будет максимальна и составит 26 123 481 рублей.