Презентация "Метод математического моделирования" – проект, доклад
Презентацию на тему "Метод математического моделирования" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Разные. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
ММЧ – метод моделирования маленькими человечками
Как возник этот метод. В синектике, ее автор, американец Гордон предложил участникам процесса решения задач на определенном этапе применять так называемую ...Метод управленческого консультирования. Консалтинг.
Метод управленческого консультирования. Управленческое консультирование - это предоставление независимых советов и помощи по вопросам управления, ...Метод Сократа
Сократ — жил в 469-399 годах до нашей эры. Древнегреческий философ из Афин, один из родоначальников диалектики. Сократ утверждал, что сам он «ничего ...Метод синектики
СИНЕКТИКА. метод коллективной творческой деятельности, основанный на целенаправленном использовании интуитивно-образного, метафорического мышления ...Метод наблюдения
Наблюдение. общенаучный метод исследования. Он применяется и как ведущий метод, и как дополнительный – подкрепляющий (например, при опросе). Он является ...Метод наблюдения
Наблюдение – это…. метод познания какого-либо процесса или явления путем целенаправленного, планомерного, непосредственного их восприятия, прослеживания ...История создания математического анализа
Математи́ческий ана́лиз — совокупность разделов математики, посвящённых исследованию функций и их обобщений методами дифференциального и интегрального ...Метод Дельфи
История разработки метода. Метод Дельфи разрабатывался в 50-60-е годы XX века в США. Основной его задачей было прогнозирование воздействия научных ...Метод капитализации доходов
Это метод оценки, применяемый в рамках доходного подхода, при котором стоимость объекта определяется путем деления текущих (за год) доходов, от использования ...Метод «Морфологический анализ»
Создание метода. В современном виде морфоанализ создан швейцарским астрофизиком Ф. Цвикки. В 30-е годы ХХ века Ф. Цвикки интуитивно применил морфологический ...Метод Дельфи
Метод Дельфи (иногда дельфийский метод) был разработан в 1950—1960 годы в США для прогнозирования влияния будущих научных разработок на методы ведения ...Метод парных сравнений
Согласно методу осуществляются парные сравнения целей во всех возможных сочетаниях. В каждой паре выделяется наиболее предпочтительная цель. Конечная ...Метод исследования: Эксперимент
Эксперимент- один из основных методов научного познания вообще, психологического исследования в частности. ЭКСПЕРИМЕНТ (от лат. experimentum — проба, ...Итерационные методы решения линейных алгебраических систем1. Метод простой итерации или метод Якоби
Предположим, что диагональные элементы матриц A исходной системы не равны 0 (aii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно ...Метод фокальных объектов
– метод поиска новых идей путем присоединения к исходному объекту свойств или признаков случайных объектов. Применяется при поиске новых модификаций ...Метод контрольных вопросов (МКВ)
«Вопрос есть повивальная бабка, помогающая родиться новой мысли…» Сократ. Древнегреческий философ Сократ умел в диалоге так искусно задавать вопросы, ...Метод эквивалентного генератора
Суть метода эквивалентного генератора состоит в нахождении тока в одной выделенной ветви, при этом остальная часть сложной электрической цепи заменяется ...Метод мозгового штурма
Сущность метода мозгового штурма заключается в том, что отбирается группа квалифицированных экспертов, но оценки и выводы делаются в ходе заседания. ...В чем секрет моделирования?
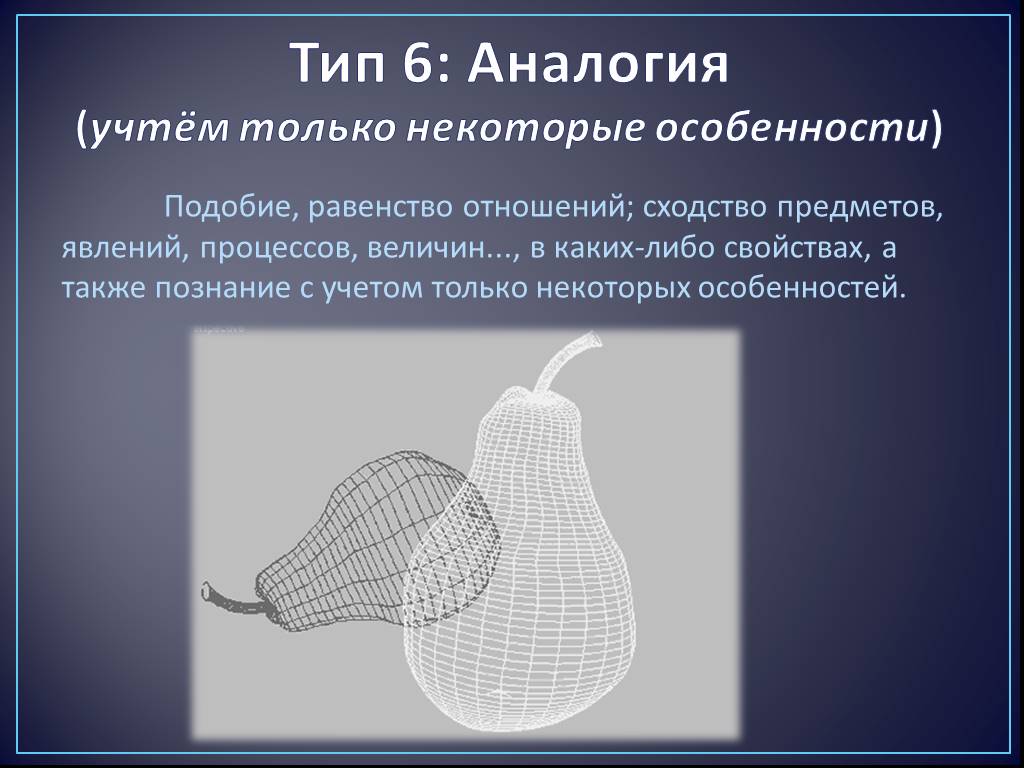
Для чего нам нужно моделирование? Это важно знать, т.к. информационные модели могут имитировать существенные черты объектов-оригиналов и достаточно ...Многокритериальные задачи. Метод ограничений
Общие сведения о многокритериальных задачах. Впервые проблема многокритериальной оптимизации возникла у итальянского экономиста В. Парето при математическом ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:13 февраля 2019
Категория:Разные
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию