Презентация "История развития тригонометрии" по математике – проект, доклад
Презентацию на тему "История развития тригонометрии" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 24 слайд(ов).
Слайды презентации
Список похожих презентаций
История развития понятия функции
История развития понятия функции. Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании ...История тригонометрии
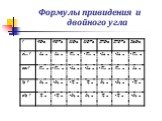
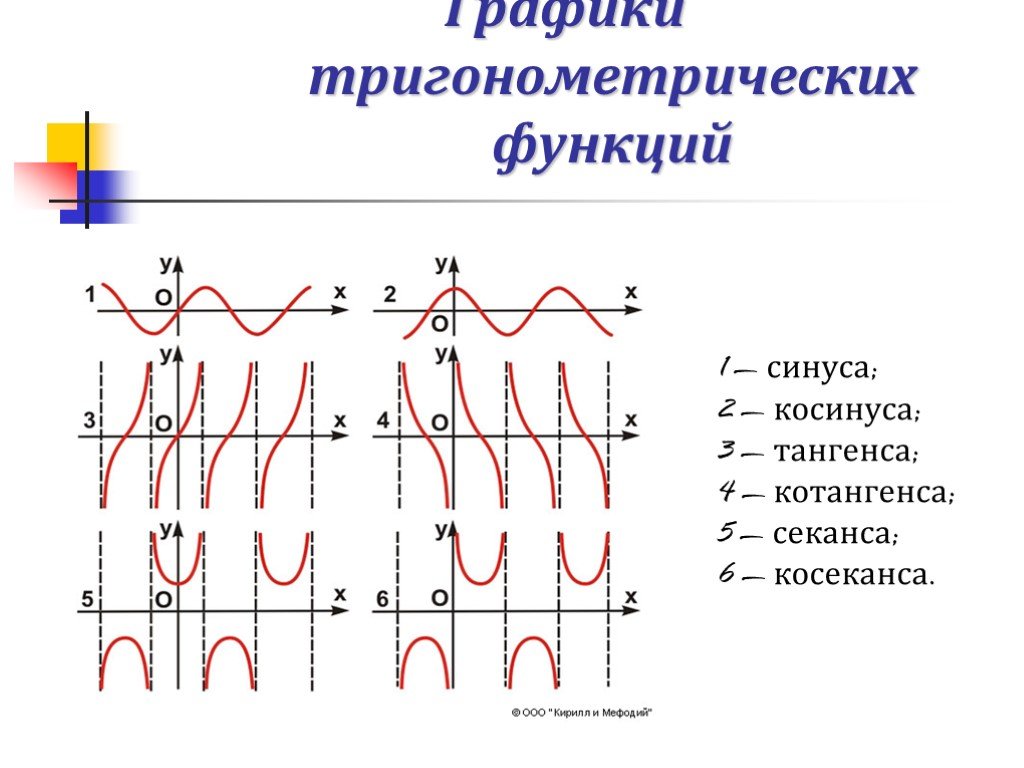
Содержание. Определения История Синус, косинус, тангенс Дальнейшее развитие Аналитическая теория Список литературы. Определения. Тригономе́трия-от ...История развития геометрии
ВВЕДЕНИЕ:. Геометрия возникла очень давно, это одна из самых древних наук. Геометрия (греческое, от geо — земля и metrein — измерять) - такое название ...История развития математики
Содержание Математика - это ? Возникновение арифметики и геометрии. Древний Восток Вавилон Древняя Греция Заключение. Математика - это наука, исторически ...История развития математики
Палеолит. Первоначальные представления о числе и форме. Неолит. Развитие ремёсел: Гончарное Ткацкое Плотническое. Счёт австралийских племён:. Племя ...История развития понятия функции
Функции, как и живые существа, характеризуются своими особенностями. П. Монтель. Идея функциональной зависимости восходит к древности. Ее содержание ...История возникновения и развития математики"
«Учиться можно только весело … Чтобы переваривать знания, надо поглощать их с аппетитом» Анатоль Франс. Цели урока:. 1.Обобщить начальные сведения ...История тригонометрии
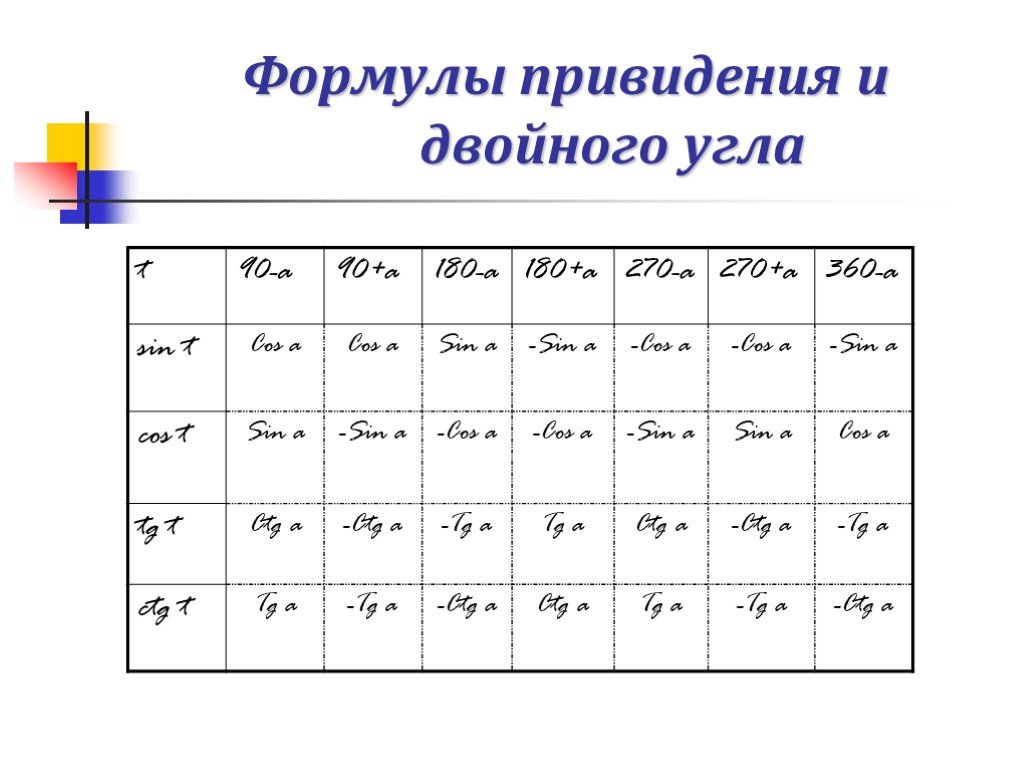
Издавна установилась такая практика, что при систематическом обучении математике ученику приходится встречаться с тригонометрией трижды. Соответственно ...История возникновения и развития математики
ХОД ИГРЫ. 1. Решить уравнения: а)4,7y-(2,5y+12,4)=1,9 б)3,5x-(2,3x-3,8)=4,28. «Первая тройка». Витя Верхоглядкин отыскал правильную дробь, которая ...Математическая сказка "История одного числа"
Содержание Часть1. «Слезы…слезы…слезы.. Часть2.Волшебная ночь Часть3. Чудесное превращение. Часть 1. Ой-ё-ей !-послышался горький плач. Это плакало ...История чисел и системы счисления
Содержание. Понятие «системы счисления» История чисел Виды систем счисления Непозиционные системы счисления Позиционные системы счисления Арабская ...История цифр
Цель: Узнать историю возникновения арабских цифр Основные задачи: Определить, как появились цифры Выяснить, как считали древние люди, которые не знали ...История теории вероятности
Человечество всегда стремилось к некоторого рода предсказаниям. Любая наука основана на этом. Однако предвидение фактов не может быть абсолютным, ...История счета и систем счисления
Все есть число! Цифры – символы для изображения чисел. Система счисления – это совокупность приемов и правил для обозначения и именования чисел. Системы ...История алгебры
Приблизительно в 850 году н.э. арабский ученый математик Мухаммед бен Муса ал-Хорезм (из города Хорезма на реке Аму-Дарья) написал книгу об общих ...Уравнения в тригонометрии
Цели урока. Образовательные: обобщить знания по теме «Решение простейших тригонометрических уравнений», проверить практические навыки и умения учащихся ...История возникновения интеграла
Архимед определил длину окружности и площадь круга, объем и поверхности шара. При этом Архимед разработал и применил методы, предвосхитившие созданное ...История возникновения дробей
Введение. В 5 классе на уроках математики мы познакомились с новыми числами – с дробями. Мне стало интересно узнать: Откуда произошли такие числа? ...История возникновения десятичных дробей
Содержание Введение………………………..………..……………………………………..3 Новая запись чисел……………………….………………………………5 Из истории десятичных и обыкновенных дробей………8 Действия ...История возникновения Геометрии
Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для ...Конспекты
История возникновения и развития геометрии. Начальные геометрические сведения
Урок геометрии с использованием ИКТ. . Класс:. 7. Учитель:. Петрова Марина Николаевна,. учитель математики МБОУ СОШ №76. . Орджоникидзевского ...Решение задач по механике с использованием тригонометрии
Муниципальное общеобразовательное учреждение. Средняя общеобразовательная школа № 34 города Томска. Конспект интегрированного урока ...Основы тригонометрии
Учитель математики первой категории Славкина Надежда Владимировна ОСШ №39 имени М.Жумабаева города Шымкента,. . Южно-Казахстанской области. ...Компетентностно-ориентированные задания на уроках математики, как фактор развития предметной грамотности учащихся
Ульянич Елена Васильевна. КГУ «Средняя школа № 17 акимата города Рудного». Мастер – класс. Тема:. «Компетентностно-ориентированные задания на ...История чисел. Запись чисел
. ПЛАН-КОНСПЕКТ. Тема: История чисел. Запись чисел. Родыгина Людмила Николаевна. . МОУ-сош №3 г.Красный Кут. . Учителя математики. . ...История чисел
Краевое государственное казённое образовательное учреждение. «Камчатская санаторная школа – интернат». Елизовского района Камчатского края. . ...История Ульяновска в числах
Технологическая карта урока. Данные об учителе: Хренкова Нина Александровна. Предмет: математика Класс: 6 ...История Нововаршавской школы в задачах на умножение дробей
Интегрированный урок по математике с элементами краеведения по теме "История Нововаршавской школы в задачах на умножение дробей", 6-й класс. . ...История возникновения чисел. Магическое значение чисел в нашей жизни
. Научно-практическая конференция школьников. . «Шаг в науку». секция «Математика». . История возникновения чисел. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 сентября 2018
Категория:Математика
Содержит:24 слайд(ов)
Поделись с друзьями:
Скачать презентацию









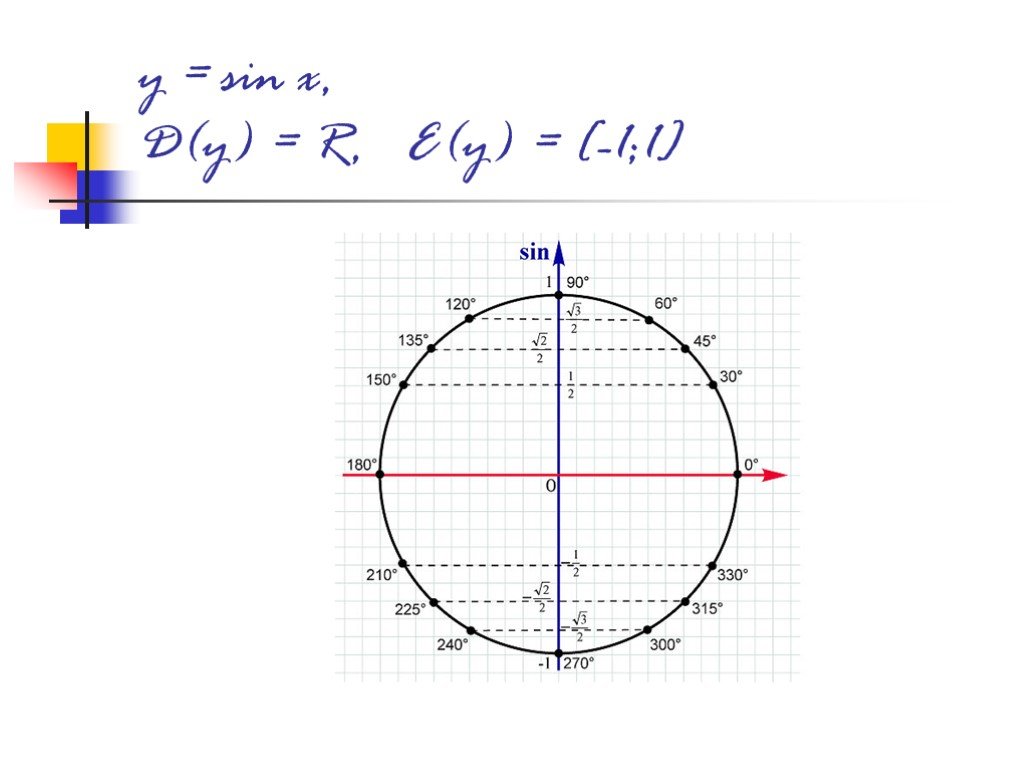


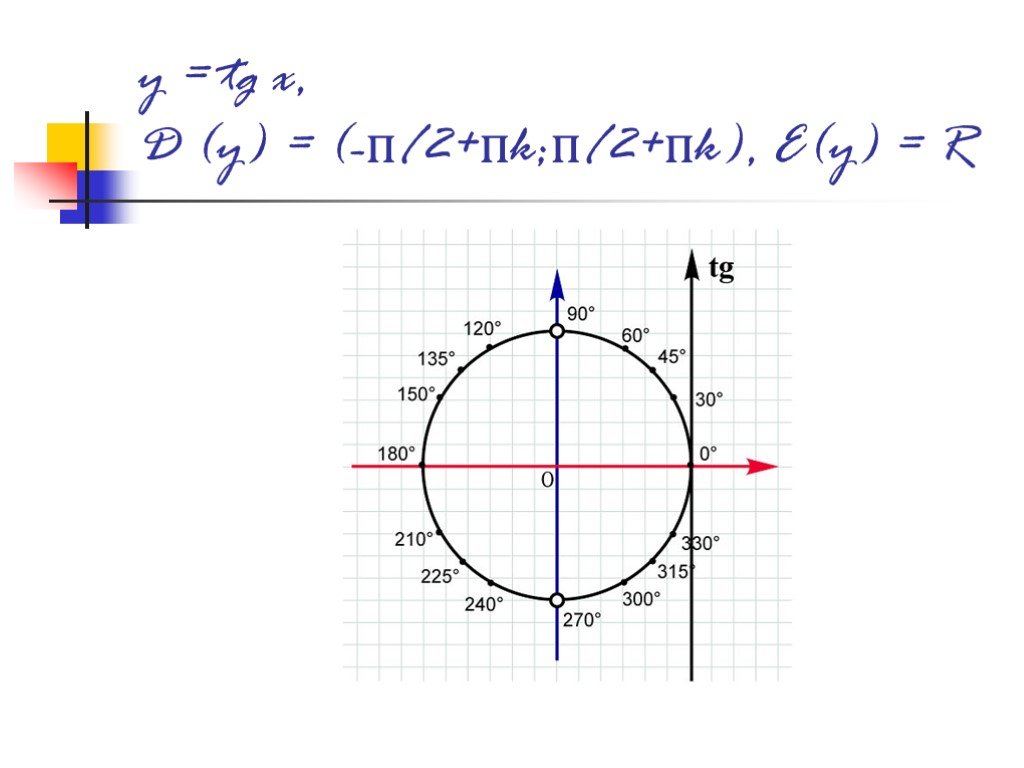
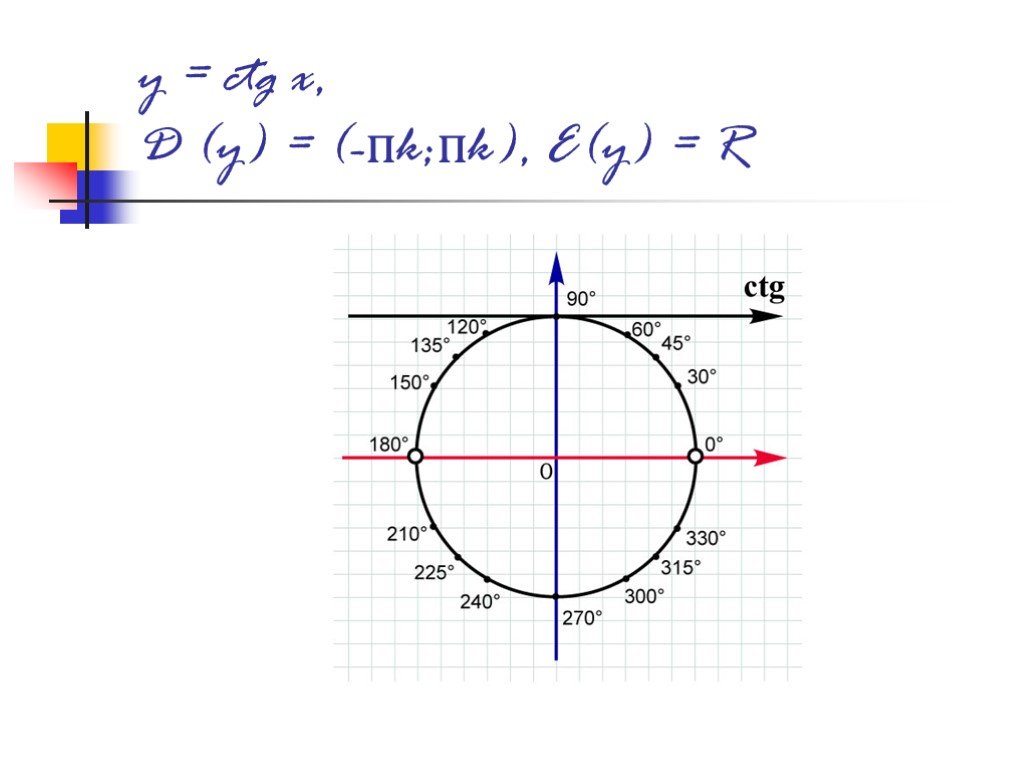

















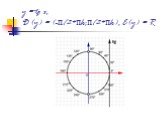
![y = sin x, D(y) = R, E(y) = [-1;1] y = sin x, D(y) = R, E(y) = [-1;1]](https://prezentacii.org/upload/cloud/18/09/79533/images/thumbs/screen10.jpg)

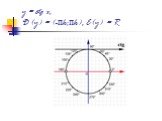
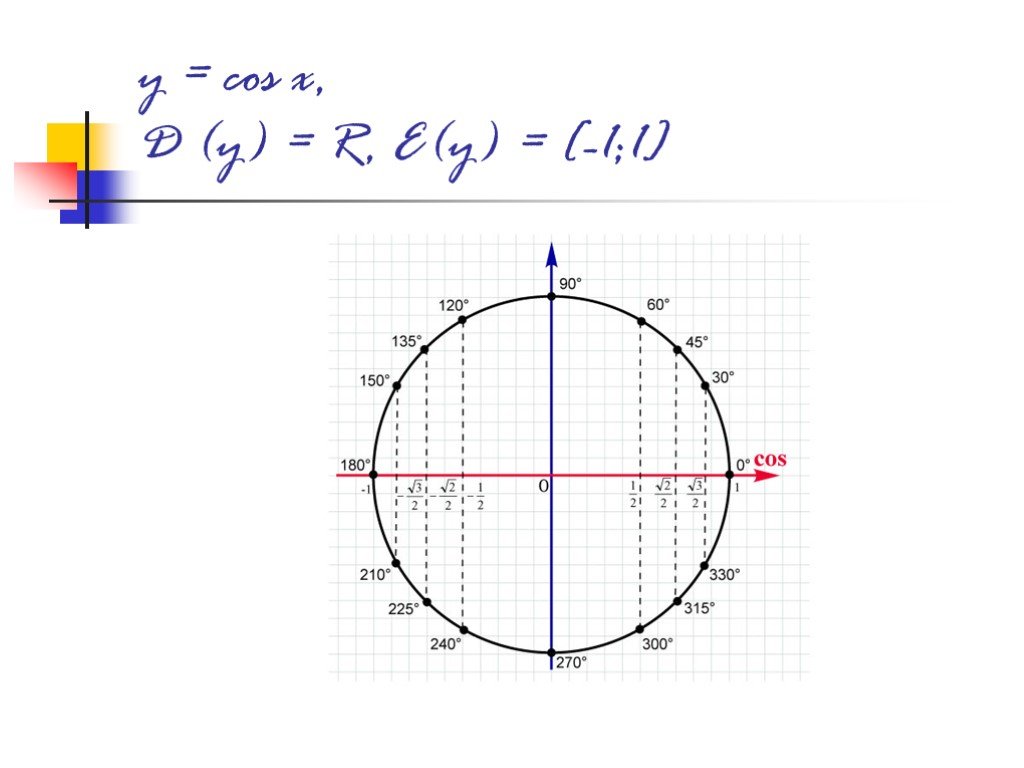
![y = cos x, D (y) = R, E(y) = [-1;1] y = cos x, D (y) = R, E(y) = [-1;1]](https://prezentacii.org/upload/cloud/18/09/79533/images/thumbs/screen12.jpg)