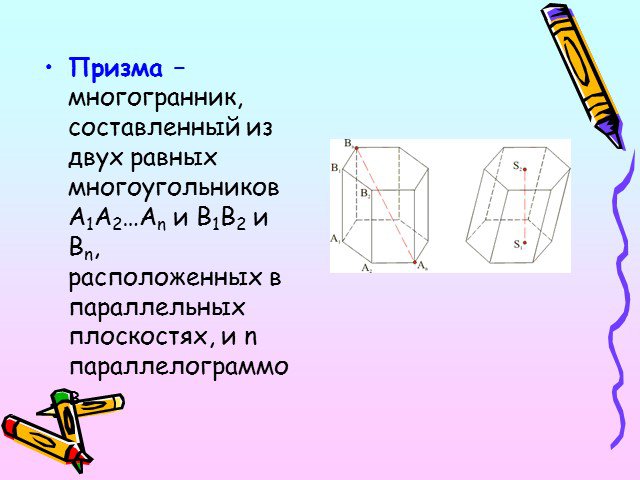
Презентация "Объем прямой призмы" по математике – проект, доклад

Объем прямой призмы

Цели урока:

Вспомнить понятие призмы. Изучить теорему об объеме призмы. Провести доказательство. Применить полученные знания на практике.

Призма – многогранник, составленный из двух равных многоугольников A1A2…An и B1B2 и Bn, расположенных в параллельных плоскостях, и n параллелограммов.

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой. Прямая призма называется правильной, если её основания – правильные многоугольники.

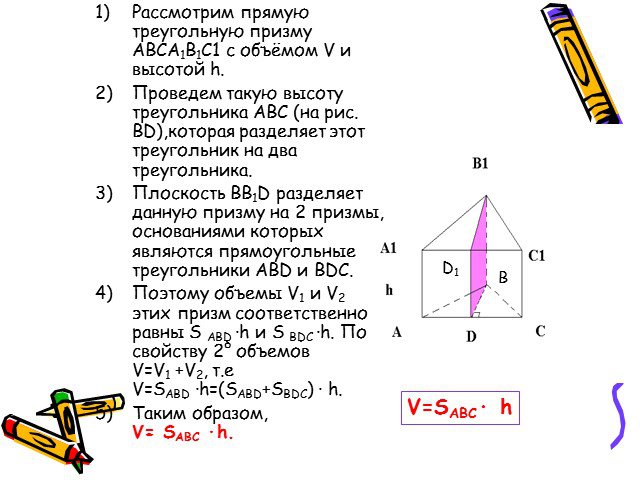
Теорема: Объем прямой призмы равен произведению площади основания на высоту

Доказательство Сначала докажем теорему для прямоугольной призмы, а затем –для произвольной прямой призмы.

В D1 А1 В1 С1 А C D

Рассмотрим прямую треугольную призму ABCA1B1C1 с объёмом V и высотой h. Проведем такую высоту треугольника ABC (на рис. BD),которая разделяет этот треугольник на два треугольника. Плоскость BB1D разделяет данную призму на 2 призмы, основаниями которых являются прямоугольные треугольники ABD и BDC. Поэтому объемы V1 и V2 этих призм соответственно равны S ABD ·h и S BDC ·h. По свойству 2° объемов V=V1 +V2, т.е V=SABD ·h=(SABD+SBDC) · h. Таким образом, V= SABC ·h.

V=SABC∙ h

Теорема для произвольной прямой призмы с высотой h и площадью основания S.

Такую призму можно разбить на прямые треугольные призмы с высотой h. На рис. изображена пятиугольная призма, которая разбита на три прямоугольные призмы. Выразим объем каждой прямоугольной призмы по формуле V= SABC ·h и сложим эти объемы. Мы вынесем за скобки общий множитель h, потом получим в скобках сумму площадей оснований треугольных призм, т.е. площадь S основания исходной призмы. Таким образом, объем исходной призмы равен произведению S · h.

Задача

Дано: ABCA1B1C1- прямая призма. AB=BC=m; ABC= φ, BD- высота в ∆ ABC; BB1=BD. Найти: VABCA1B1C1-?

Решение:

S ABC ·h, h=BB1. Рассмотрим ∆ ABC; ∆ ABC- р/б. BD- высота ∆ ABC, следовательно медиана и биссектриса. ABD= DBC= φ/2 3) Рассмотрим ∆ ABD; ∆ ABD- прямоугольный. Из соотношения в ∆: cosφ/2 = BD/AB BD= cosφ/2 AB, BD=m cosφ/2 (AB=m) 4) Т.к. BD=BB1 BB1=m · cos φ /2 5) S ABC= ½ AB·BC· sinφ; S ABC= ½ m2 · sinφ 6) V= ½ m2 · sinφ· mcosφ/2=½ m3 · sinφ · cosφ/2 Ответ: ½ m3 · sinφ · cosφ/2

Вопросы:

Как найти объем прямой призмы? Основные шаги при доказательстве теоремы прямой призмы?

Работу выполнили: Шахбазян Эллена,11”В” Шмырева Юлия,11 “В” Двадненко Аня,11 “В”

СПАСИБО ЗА ВНИМАНИЕ =)