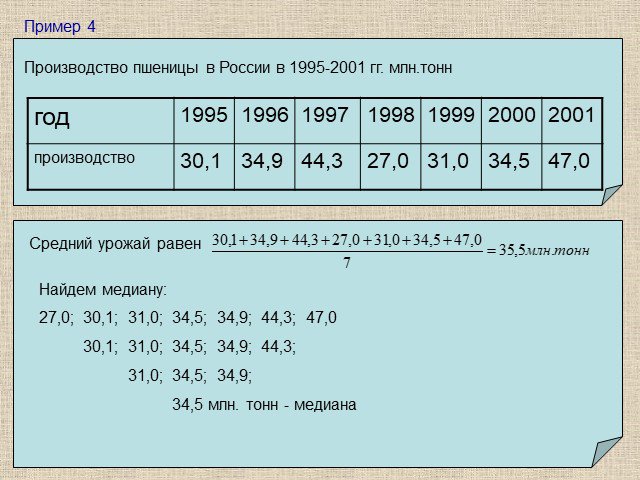
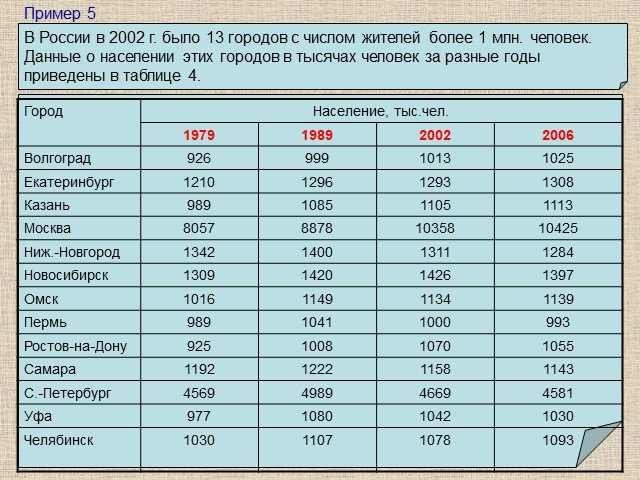
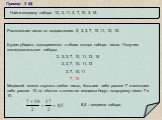
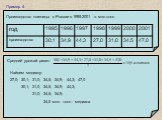
Презентация "Медиана" по математике – проект, доклад
Презентацию на тему "Медиана" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 17 слайд(ов).
Слайды презентации
Список похожих презентаций
Медиана, биссектриса и высота треугольника
C O E A B D. Высота треугольника. Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины к прямой, ...Медиана, биссектриса, высота треугольника
Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Биссектриса – это отрезок биссектрисы угла треугольника, ...Медиана, биссектриса и высота треугольника
отрезок, соединяющий вершину треугольника с серединой противолежащей стороны Биссектриса треугольника Медиана треугольника Высота треугольника. Подумай ...Конспекты
Медиана, биссектриса, высота треугольника
Урок по теме «Медиана, биссектриса, высота треугольника». Разработала учитель математики МБОУ СОШ №2 с. Александров-Гай Уразова Ольга Владимировна. ...Медиана, биссектриса и высота треугольника
Шангина Ирина Евгеньевна, учитель математики ОУ СОШ № 11 г.Октябрьска Самарской области. . Урок геометрии в 7 классе. Тема:. Медиана, биссектриса ...Медиана как статистическая характеристика
Конструкт урока по математике. Класс 7, общеобразовательный. Тема «Медиана как статистическая характеристика». Цель:. рассмотреть понятие медианы ...Медиана, биссектриса и высота треугольника
Автор: Добриян Валентина Васильевна. учитель математики. Лингвистическая школа- лицей. Материал скачан со страницы: http://pedsovet.su/load/136-1-0-8996. ...Медиана как статистическая характеристика
Урок 20. Тема урока:. «Медиана как статистическая характеристика». Предмет:. Алгебра. . Тип занятия:. закрепление изученного материала. . ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 сентября 2014
Категория:Математика
Автор презентации:Бахова А.Б.
Содержит:17 слайд(ов)
Поделись с друзьями:
Скачать презентацию