Презентация "Решение систем неравенств" (9 класс) по математике – проект, доклад
Презентацию на тему "Решение систем неравенств" (9 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 16 слайд(ов).
Слайды презентации
Список похожих презентаций
Итоговый урок: решение систем уравнений
ЦЕЛИ УРОКА. 1. повторить определения понятий: -система уравнений; -решение систем уравнений; -способы решения систем уравнений. 2. Найти практическое ...Решение дробно-рациональных неравенств
Цели урока:. Повторить решение рациональных неравенств методом интервалов; Обобщить метод интервалов для решения дробно-рациональных неравенств; Закрепить ...Графическое решение систем уравнений
Правило решения системы уравнений графическим способом. Построить графики каждого из уравнений системы. Найти координаты точки пересечения построенных ...Ох уж эти показательные… Решение показательных уравнений и неравенств
Ответьте на вопросы. 1. Какая функция называется показательной? 2. Какова область определения показательной функции? 3. Какова область значений показательной ...Графическое решение систем уравнений
Лаборатория «ТРУД». Твори, Решай, Учись, Добивайся с интересом и удовольствием! Руководители лаборатории. Начальник лаборатории: Ноумэн Ноу Мэнович ...Примеры логарифмических неравенств
Цели урока:. 1. Систематизировать и обобщить знания по теме «Логарифмические неравенства». 2. Повторить основные методы решения логарифмических неравенств. ...Приемы доказательства неравенств, содержащих переменные
Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь ...Повторение. Проценты. Решение задач
Будем знакомы. Я - Компик. Сегодня на уроке мы вместе вспомним понятие процента. Конечно же порешаем задачи на эту тему. Желаю всем УДАЧИ! Если вы ...Описание линейных дискретных систем во временной области
Дискретным называется сигнал, дискретный во времени и непрерывный по состоянию. Он описывается решетчатой функцией (последовательностью) x(nT), где ...Алгебра высказываний. Решение логических задач
Задача 1: Составьте сложное высказывание в словесной форме из простых, заданных математическим формулировкам:. Высказывание А: «Учащийся Иванов хорошо ...Решение задач 4 класса
Цели и задачи урока. развивать вычислительные навыки; совершенствовать умение решать задачи с величинами: скорость, время, расстояние; закреплять ...Решение задач
Задача 1. У Тани было 5 белых котят. 3 котика убежали. Сколько котят осталось? Решение: 5 – 3 = 2 (к.) Ответ: 2 котёнка. Задача 2. В вазе лежало 3 ...Блок-схема для решения квадратных неравенств
Неравенства второй степени вида. D. D=0 x=m m. D>0 m n. . . . . . . . Нет решения. . . . . . . . . Тренажер. решение квадратных неравенств. Варианты ...Блиц-опрос "Решение треугольников"
Выбери вопрос. В треугольнике АВС угол А равен 40 градусов. Внешний угол при вершине В равен 68 градусов. Найдите угол С. Угол С равен 28 градусов. ...Бинарный урок геометрии и информатики "Четырехугольники. Решение задач" Лауреат
Проверка домашнего задания. В трапеции АВСD (АD – большее основание) диагональ АС ┴СD и делит ВАD пополам, СDА=60, периметр трапеции – 20 см. Найдите ...Арксинус. Решение уравнения sin t = a
Цели. Изучить определение арксинуса числа. Изучить формулы решения простейшего тригонометрического уравнения sin t = a. Повторим. Что называется синусом ...Аналитический и численный методы решения систем уравнений с параметром
АНАЛИТИЧЕСКИЙ И ЧИСЛЕННЫЙ МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ С ПАРАМЕТРОМ. Астрахарчик Н.А. Система симметрична относительно знака x. Система симметрична ...Алгоритм решения неравенств
Для любых двух простейших чисел а и в выполняется одно из двух условий: либо а больше в (а>в), либо а меньше в (а. Возникает задача: найти все – значения ...Прямая и обратная пропорциональнось. Решение задач
План урока. Повторение и систематизация теоретических знаний. Повторение и систематизация практических умений. Самостоятельная работа Подведение итогов. ...Аксиомы стереометрии Решение задач
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...Конспекты
Перебор слов и системы счисления. Решение задач
План - конспект урока по математике в 9-классе. Тема урока «Перебор слов и системы счисления. Решение задач». Автор: Житенева Олеся Владимировна, ...Решение задач (Урок повторения и обобщения изученного)
Математика 3 класс Школа 2100. 24 апреля. Тема:. Решение задач (Урок повторения и обобщения изученного). Цели: 1. Совершенствовать вычислительные ...Решение задач
7. . . Тема урока. : Решение задач. . Цели:. . . привести в систему все виды изученных задач;. . отрабатывать умение решать задачи. ...Решение задач
Тема урока: Решение задач. Цели:. - закреплять умение решать простые и составные задачи;. - совершенствовать вычислительные навыки;. - развивать ...Решение задач
Урок геометрии для 7 класса «Решение задач». . Цель:. обзорное повторение материала, изученного за год;. Задачи урока:. проверить усвоение ...Решение двухшаговых уравнений
Тема:. Решение двухшаговых уравнений. . . Цели:. 1) научить находить неизвестное слагаемое в уравнении вида: х+15=68:2;совершенствовать вычислительные ...Проценты. Решение задач открытого банка ФИПИ
ПЛАН-КОНСПЕКТ УРОКА. 1. ФИО. 2. Место работы. 3. Должность. 4. Предмет. 5. Класс. 6. Тема и номер урока в теме. 7. Базовый учебник. Агеева ...Прибавить и вычесть число 3. Решение текстовых задач
Разработка урока по математике «. Прибавить и вычесть число 3. Решение текстовых задач». . . Журнал «Начальная школа» (математика). Мурашкина ...Графический способ решения систем уравнений
Тема урока:. . Графический способ решения систем уравнений. Тип урока. : Урок изучения нового материала. Цели урока. :. Образовательные. ...Графический способ решения систем уравнений
. . . . . . Урок алгебры по теме. «Графический способ решения систем. уравнений». Автор: Гаврилова Ирина Николаевна. Учитель математики ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:25 апреля 2015
Категория:Математика
Классы:
Содержит:16 слайд(ов)
Поделись с друзьями:
Скачать презентацию






















![Решим систему неравенств. 5х + 12 ≤ 3х+ 20 х - 3 х ≥ -3,5 Изобразим на числовой прямой: -3,5 -3 4 Ответ: ( -3; 4] Решим систему неравенств. 5х + 12 ≤ 3х+ 20 х - 3 х ≥ -3,5 Изобразим на числовой прямой: -3,5 -3 4 Ответ: ( -3; 4]](https://prezentacii.org/upload/cloud/15/04/41221/images/thumbs/screen7.jpg)



![Решите неравенства, работая в парах. Решить неравенства: -6 ≤ - 3х ≤ 3 4. Проверим ответы: 1) [-1; 2] 2) (2,5; 7] 3) [- 1,5; - 1) 4) (-2; 1) 5) (-4; 0) Решите неравенства, работая в парах. Решить неравенства: -6 ≤ - 3х ≤ 3 4. Проверим ответы: 1) [-1; 2] 2) (2,5; 7] 3) [- 1,5; - 1) 4) (-2; 1) 5) (-4; 0)](https://prezentacii.org/upload/cloud/15/04/41221/images/thumbs/screen11.jpg)



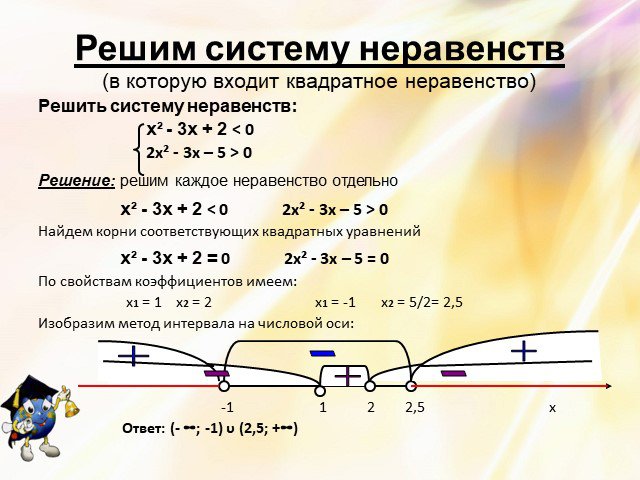
![Решите системы неравенств, работая самостоятельно. 1) х² - 10х + 9 ≥ 0 12 – 3х 0 4х – 1 ≥ 3 3) 2х² - 7х + 5. Проверим ответы: 1) (4; 9] 2) [1; 2) 3) (- ∞; 1) Решите системы неравенств, работая самостоятельно. 1) х² - 10х + 9 ≥ 0 12 – 3х 0 4х – 1 ≥ 3 3) 2х² - 7х + 5. Проверим ответы: 1) (4; 9] 2) [1; 2) 3) (- ∞; 1)](https://prezentacii.org/upload/cloud/15/04/41221/images/thumbs/screen15.jpg)