Презентация "Треугольник. Вписанная окружность" по математике – проект, доклад
Презентацию на тему "Треугольник. Вписанная окружность" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 8 слайд(ов).
Слайды презентации
Список похожих презентаций
Вневписанная окружность треугольника
Вневписанная окружность. B A C Ka K1. Kb Kc ra rb rc. Определение. Вневписанной окружностью треугольника называется окружность, касающаяся одной из ...Вписанная окружность
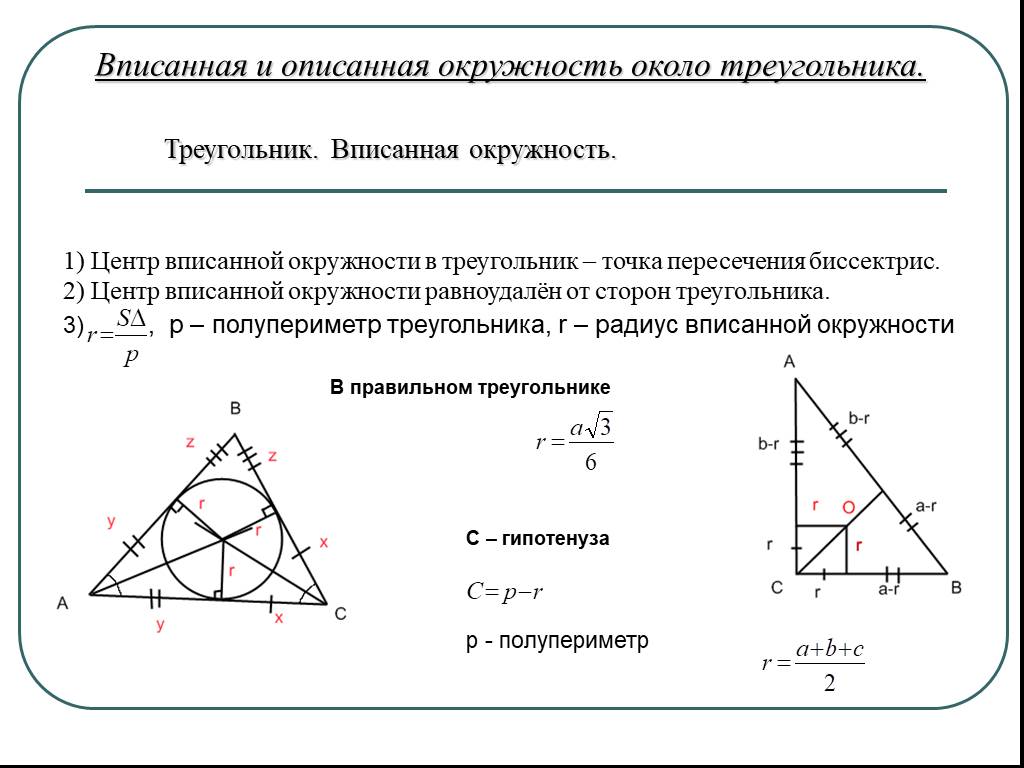
Цели урока:. 1.Познакомится с определением вписанной окружности. 2.Изучить доказательство теоремы о вписанной окружности. 3.Решение задач по данной ...Вписанная и описанная окружность
Окружность называется вписанной в многоугольник, если. все стороны многоугольника касаются данной окружности. Всегда ли можно вписать окружность в ...Вписанная и описанная окружность
АРХИМЕД (287-212 ДО Н.Э.) – древнегреческий математик и механик. Древние математики не владели понятиями математического анализа. Однако они умели ...Вписанная и описанная окружность
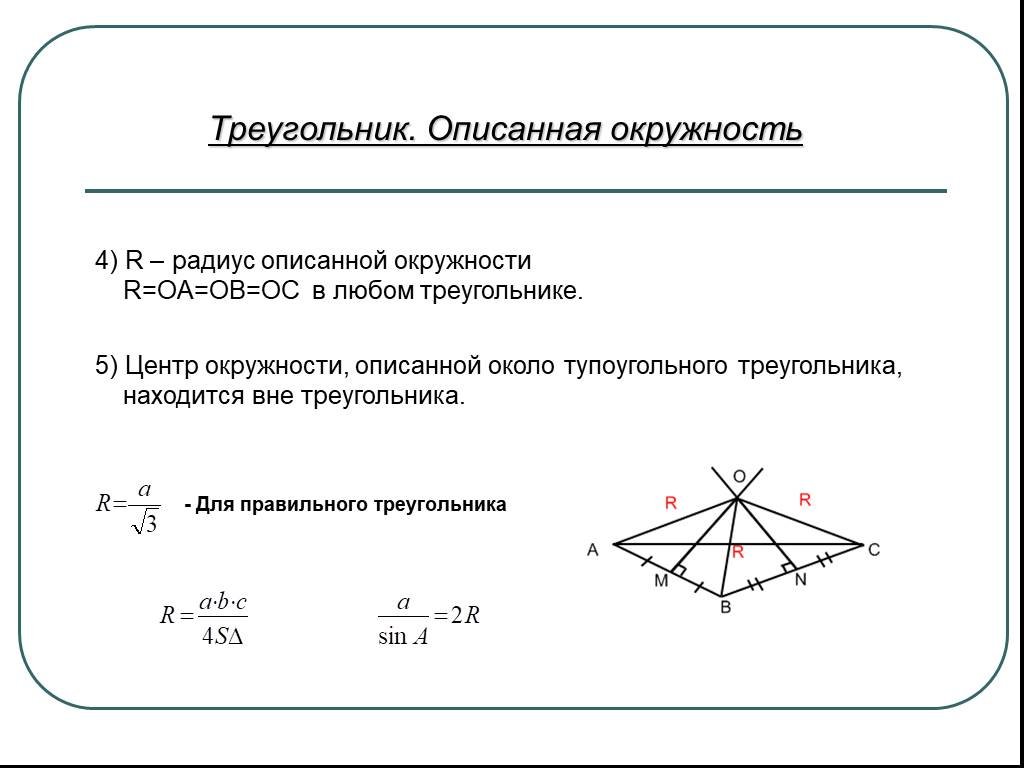
1. Окружность с центром в точке О описана около прямоугольного треугольника. Докажите, что точка О -середина гипотенузы. 2. Найдите радиус этой окружности, ...Вписанная и описанная окружность
ТЕМА: «ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ». ОБРАЗОВАТЕЛЬНАЯ ЦЕЛЬ: ВЫЯСНИТЬ КАК УЧАЩИЕСЯ УСВОИЛИ СВОЙСТВА ВПИСАННОЙ И ОПИСАННОЙ ОКРУЖНОСТЕЙ; ЗАКРЕПЛЕНИЕ ...Вписанная и описанная окружность
Вписанная окружность. Центр вписанной окружности – середина серединного перпендикуляра к основаниям Если О- центр вписанной окружности, то СОD =90. ...Вневписанная окружность
Содержание. Введение. Основная часть Глава 1. Определение вневписанной окружности. Центр вневписанной окружности. Касательная к вневписанной окружности. ...Описанная около многоугольника окружность
Многоугольники, описанные около окружности. Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности. Сама ...Невозможное возможно. Треугольник Пенроуза
Треугольник Пенроуза. На уроках математики мы познакомились с разными видами треугольников:-остроугольными, прямоугольными,тупоугольными.На уроках ...Круг и окружность
Цель работы. исследование зависимости между радиусом, длиной окружности и площадью круга. Где используются круги Круги используются в колёсах машин, ...Задачи на окружность
Цели урока:. Повторить понятия: окружности и круга центра окружности радиуса окружности диаметра окружности Вывести соотношения между радиусом и диаметром. ...Задачи на вписанную окружность
Математический К В Н. Вписанная окружность. Определение: Если все стороны многоугольника касаются окружности, то окружность называется вписанной в ...Единичная окружность
Окружность радиусом 1 см. 1 см О D С В А Длина окружности:. Длина половины окружности (АС):. Длина четверти окружности (АВ, ВС, СD, DA):. I II III ...Описанная окружность
. . Как вписать \ описать нам окружность счастья? В любую ли фигуру можно вписать окружность? Около какой фигуры можно описать окружность? Вписанная ...Геометрия Евклида и геометрия Лобачевского. Сходства и отличия
Евклидова геометрия. Евкли́д или Эвкли́д (, ок. 300 г. до н. э.) — древнегреческий математик. Мировую известность приобрёл благодаря сочинению по ...геометрия решение задачи
Дано: а-прямая, A B а Построить: BC=2AB Решение:. A,B-точки на прямой,. (на луче BA). Измерим циркулем расстояние между A и B,. отложим отрезок AC ...Все вокруг - геометрия
Откуда есть, пошла «Геометрия»? Слово «геометрия» - греческое, в переводе на русский означает «землемерие». около 4000 лет тому назад жители Древнего ...Небесная геометрия
Цели и задачи. Цель: дать физическое и математическое обоснование разнообразия форм снежинок. Задачи: изучить историю появления фотографий с изображениями ...Неевклидова геометрия
Мы выбрали эту тему так как она нас очень заинтересовала тем , что геометрия Лобачевского очень полезна в современном мире, и мы хотим немного рассказать ...Конспекты
Треугольник
Спирякова С.М.,. учитель математики,. . МБОУ «Куединская СОШ №1- БШ». Класс:. 7. Тема:. «. Треугольник. ». Тип урока:. урок изучения нового ...Треугольник и его элементы. Виды треугольников
Тема: Треугольник и его элементы. Виды треугольников. ЦЕЛИ:. . 1. Изучить понятие треугольника и его элементов в ходе практической работы; виды ...Треугольник
План-конспект учебного занятия. . МКОУ «Новомирская СОШ». Учитель: Асфандиярова Лилия Муллаахматовна. Предмет: математика. Класс: 5. Место занятия ...Треугольник
Дата: _____________________. Класс: 5. Предмет: математика. . "Треугольник". Цели:. 1.Образовательные:. . ввести понятие треугольника, ...Круг и окружность
Конспект урока математики в 5 классе. Тема: «Круг и окружность». Учитель математики Воронцова О.В. Цели и задачи урока:. Обучающие:. . . ...Треугольник
Геометрия 7. Открытый урок. Тема: Треугольник. Урок-игра «Рыцарский турнир». Цели урока:. -повторение и закрепление изученного материала, ...Треугольник
Малкова Надежда Геннадьевна, МБОУ Лицей № 40, г.Нижний Новгород. . Автор. : Малкова Надежда Геннадьевна,. учитель математики МБОУ Лицей № 40 г.Нижний ...Числовая окружность
Конспект урока по алгебре. Учитель: Шиванова Сания Ягутовна. Предмет: алгебра и начала анализа. Тема урока: Числовая окружность. Класс: 10. ...Описанная окружность
Описанная окружность. Определение:. Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника. ...Треугольник
Урок наглядной геометрии в 5 классе. с применением технологии развивающего обучения. ГБОУ гимназия №402. учитель: Гальцова Олеся Анатольевна. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 мая 2019
Категория:Математика
Содержит:8 слайд(ов)
Поделись с друзьями:
Скачать презентацию