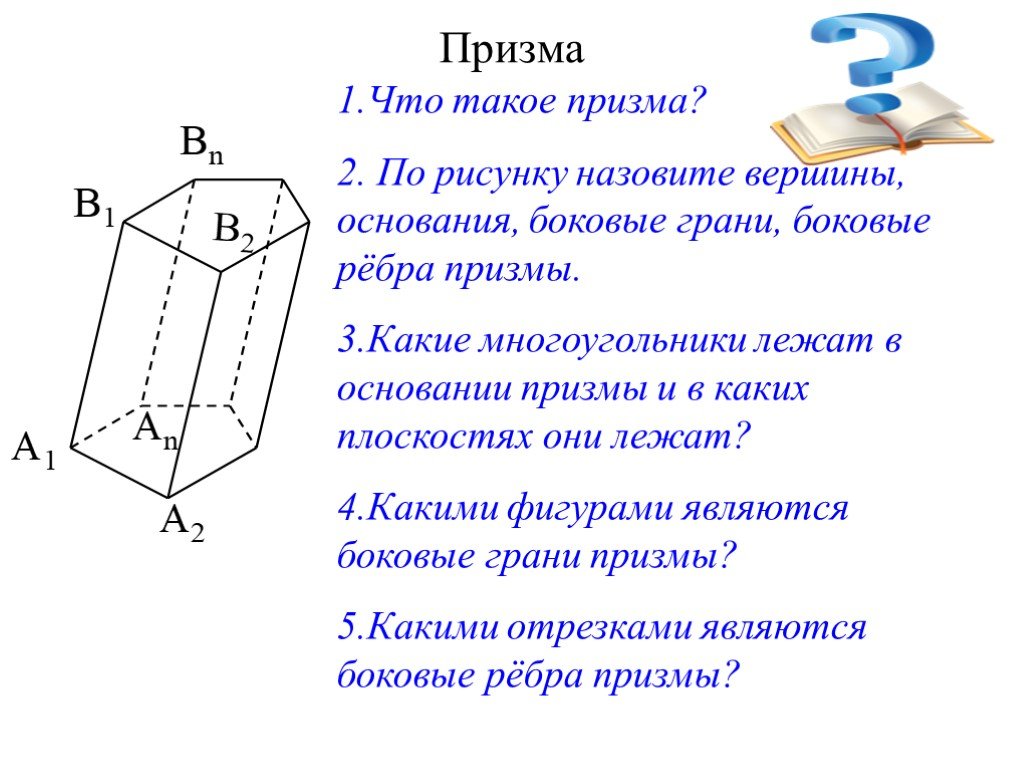
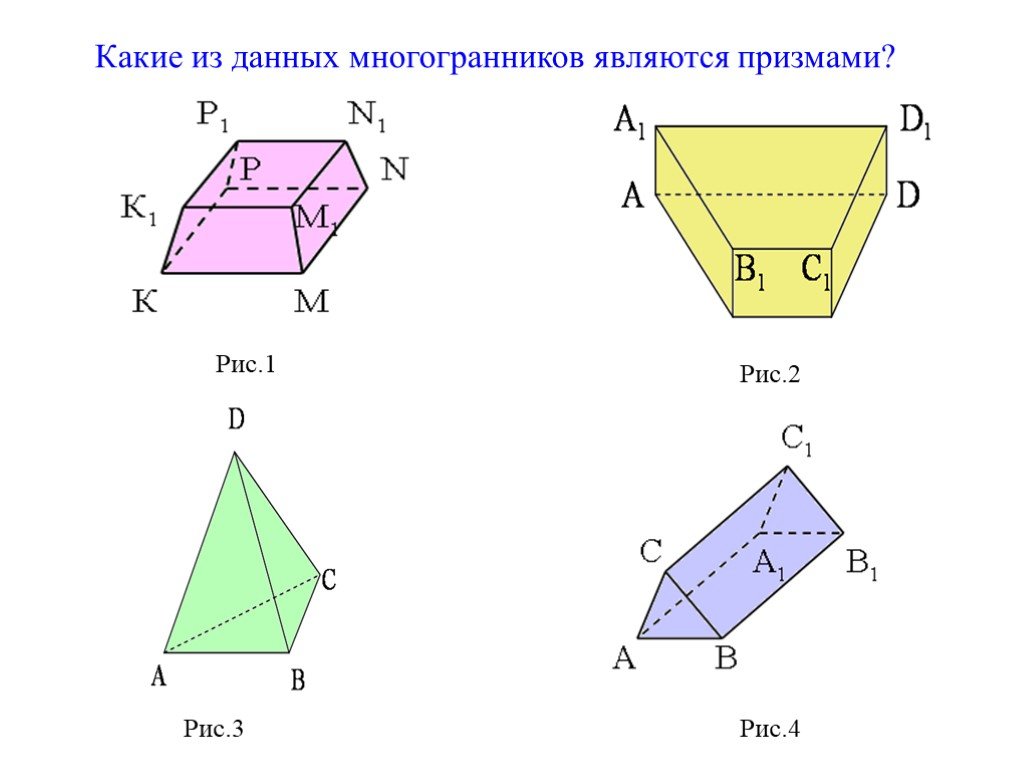
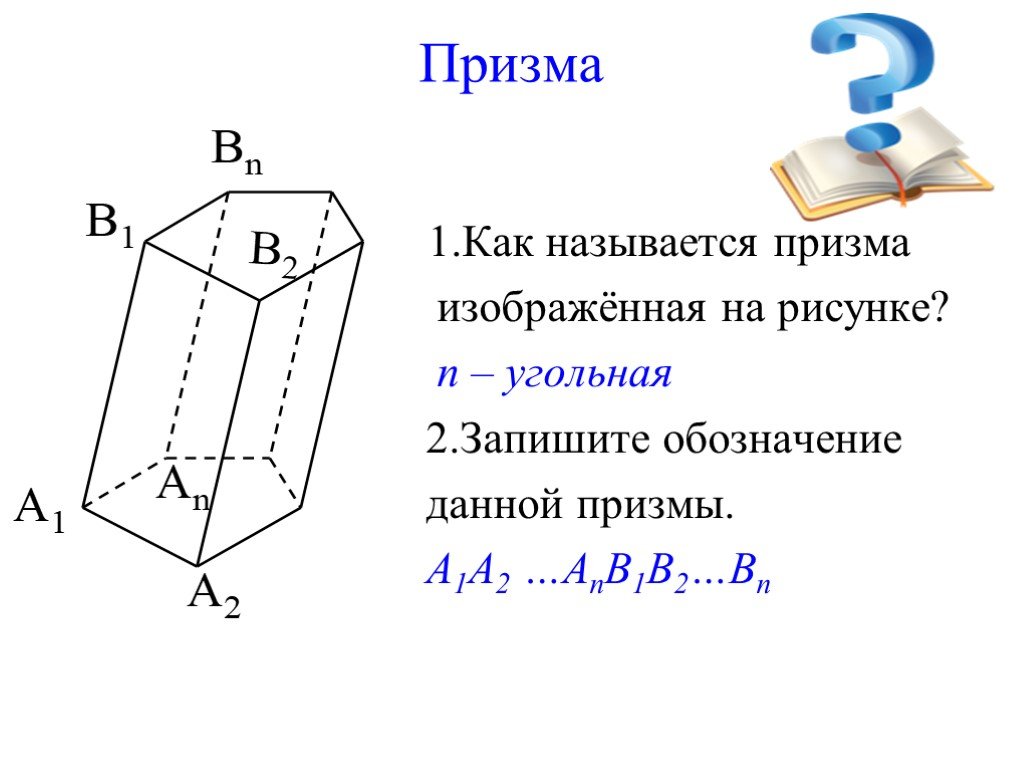
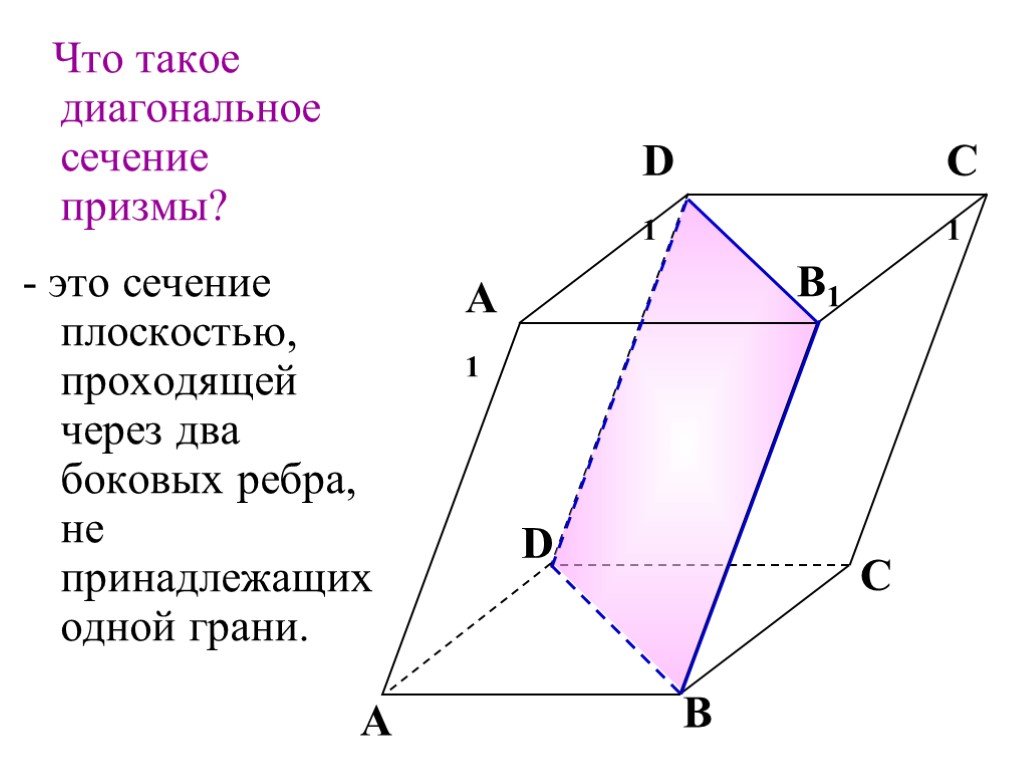
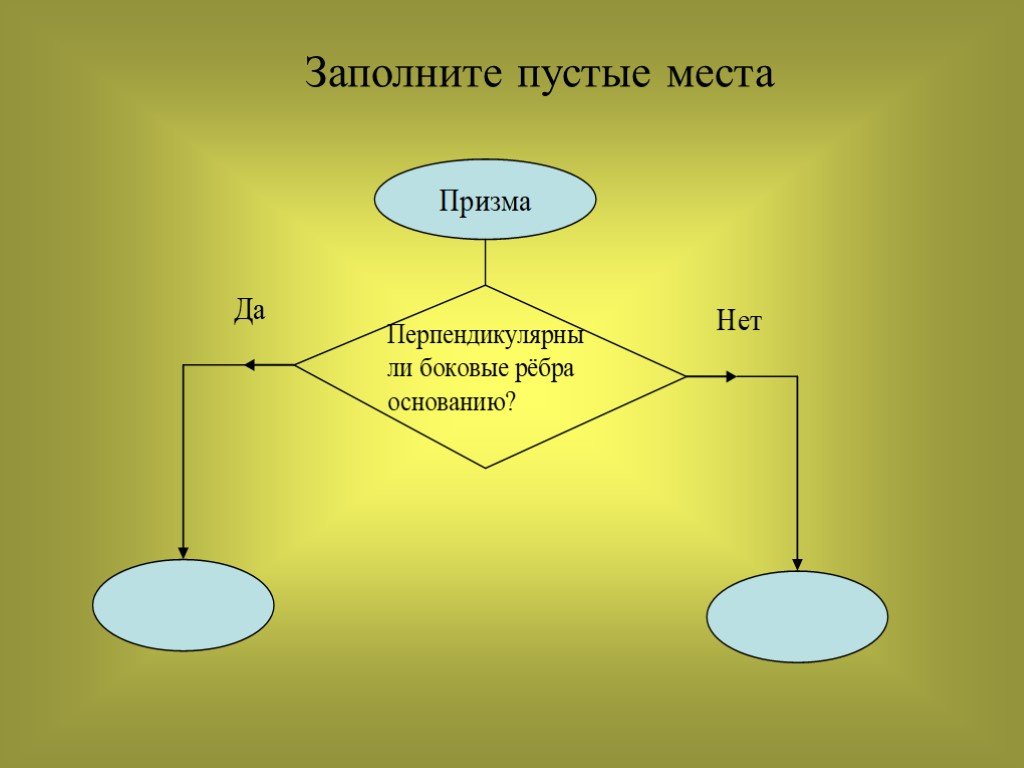
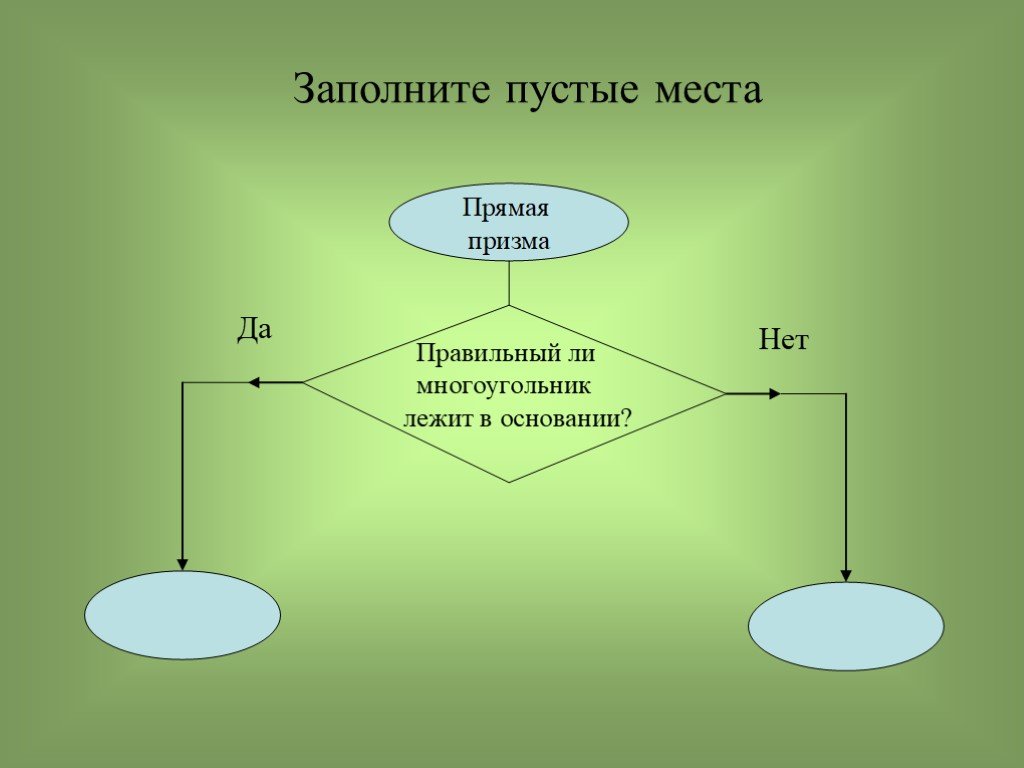
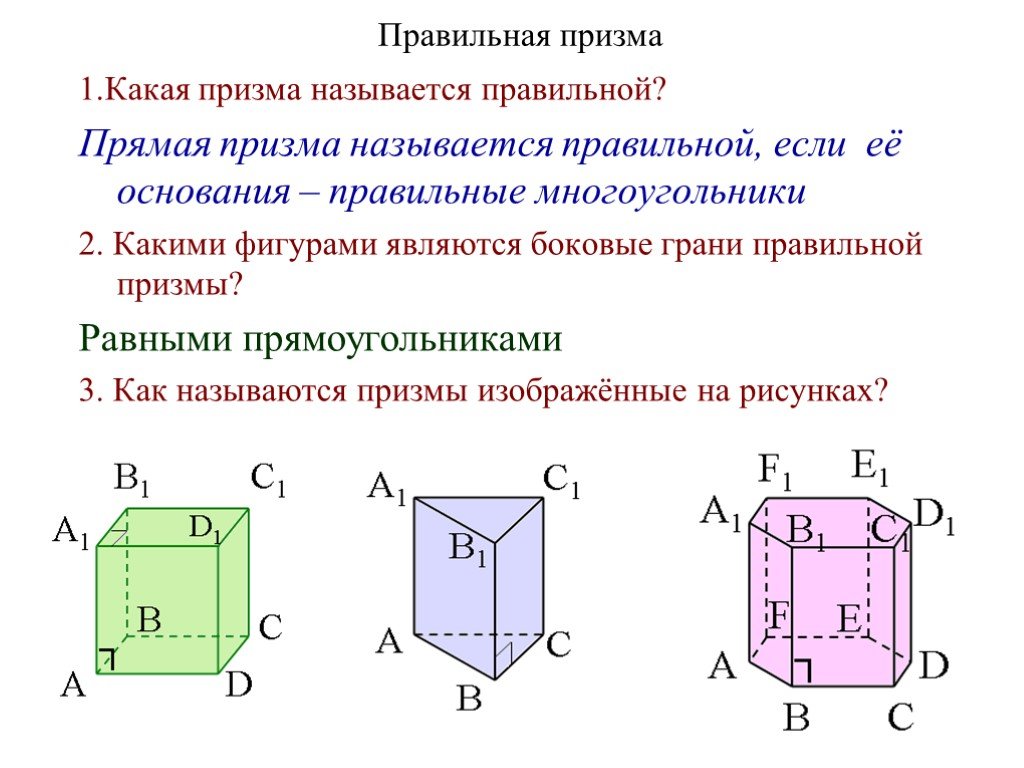
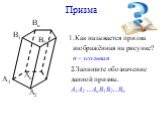
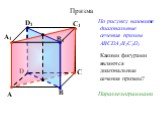
Презентация "Геометрическое тело призма" по математике – проект, доклад
Презентацию на тему "Геометрическое тело призма" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 34 слайд(ов).
Слайды презентации
Список похожих презентаций
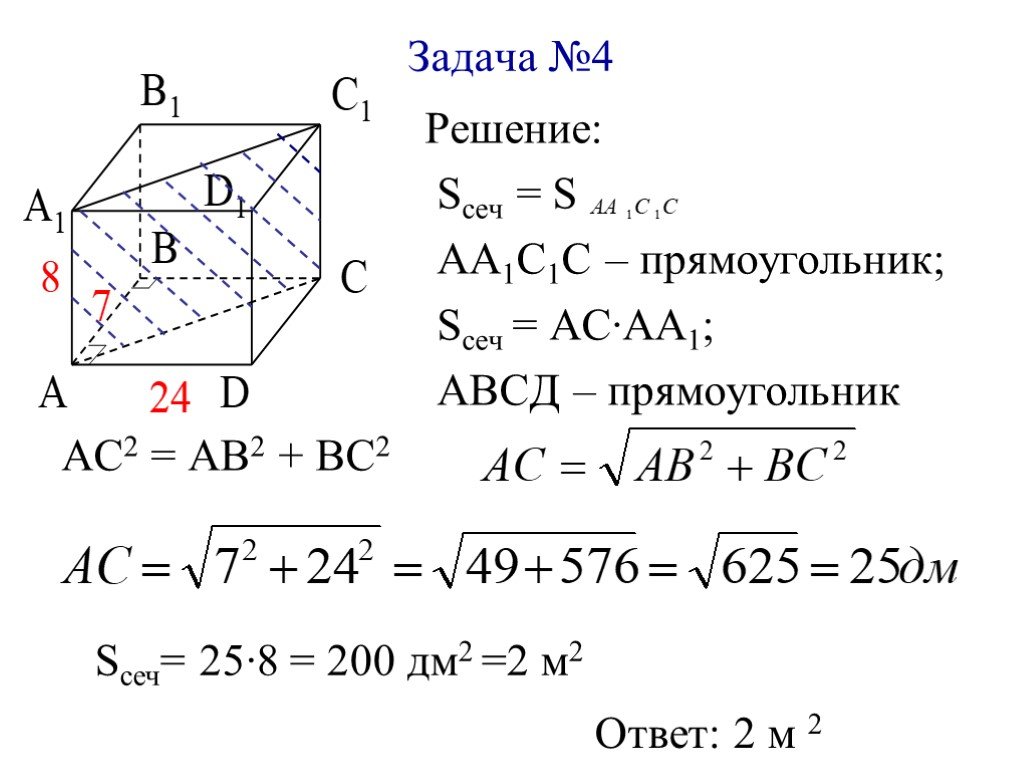
Объём. Цилиндр, призма
В цилиндрический сосуд налили 1200 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень ...Конус, пирамида, призма, цилиндр.
Цели урока. Учить учащихся навыкам и умениям определять название геометрических тел, мысленно расчленять предметы на составляющие его геометрические ...Начертательная геометрия
Начертательная геометрия изучает способы изображения пространственных форм на плоскости. . ГАСПАР МОНЖ. В 1795 году вышел труд "Начертательная геометрия" ...Что такое геометрия
Геометрия- одна из наиболее древних наук. Первые геометрические факты были найдены…. В Вавилонских клинописных таблицах и египетских папируса (III ...«Ломаная» геометрия
Найдите соответствие. Ответы. Ломаная Тема урока:. Какие из фигур являются ломаными? А Б В Г Д. Ответ А В Г. Кусок проволоки возьми И его ты перегни. ...Пчелы и геометрия
Внеклассное мероприятие «пчелы и геометрия». В природе все продумано и совершенно. Индийская пчела Украинская пчела. Австралийская пчела. Пчела - ...Фракталы – геометрия природы
Задачи:. узнать, что такое «фракталы»; изучить историю возникновения и развития фрактальной геометрии; ознакомиться с биографией создателя фракталов ...Перпендикулярность в пространстве геометрия
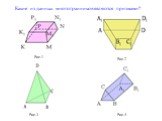
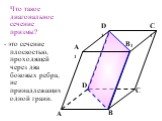
Цель:. Познакомиться с перпендикулярностью в пространстве. Проанализировать различные источники по данной теме. Выделить основные подходы к рассмотрению ...Построение сечений многогранников геометрия
Обучающая цель: формирование умений и навыков построения сечений. Развивающая цель: формирование и развитие у учащихся пространственного представления. ...Векторы геометрия
Вектора. Действия с векторами. а b. Сумма векторов. Вырази вектор АС АN AM CB CM. Произведение векторов. Выразите вектор ОМ. М – точка пересечения ...Вероятность и геометрия
Классическая вероятностная схема. Для нахождения вероятности случайного события A при проведении некоторого числа опытов следует: Найти число N всех ...Алгебра и геометрия
Комплексные числа. ׳. Содержание. § 1. Основные понятия § 2. Геометрическое изображение комплексных чисел § 3. Формы записи комплексных чисел § 4. ...В моде – геометрия
Мода 60 – ых, и поп - арт. Наряды с геометрическими формами смотрятся очень остро. В моде 1920-х годов большое влияние оказало авангардное искусство-от ...Алгебра и геометрия
История. Женщина обучает детей геометрии. Иллюстрация из парижской рукописи Евклидовых «Начал», начало XIV века. Средние века немного дали геометрии, ...«Скалярное произведение векторов» геометрия
Таблица значений для углов, равных 300, 450, 600. Заполните таблицу. Формулы приведения. sin( )= cos( )= -. Проверка д.з. № 1039 Диагонали квадрата ...«Симметрия в пространстве» геометрия
Что такое симметрия? Симметрия в переводе с греческого означает соразмерность. Под симметрией принято понимать свойство геометрической фигуры, расположенной ...Небесная геометрия
Цели и задачи. Цель: дать физическое и математическое обоснование разнообразия форм снежинок. Задачи: изучить историю появления фотографий с изображениями ...Весёлая геометрия
Точка Рано-рано, поутру Шел цыпленок по двору Вместе с мамой-квочкой. Клюнул крошку на песке – Получилась точка. Представьте: вы, ребята, – Дружные ...Неевклидова геометрия
Мы выбрали эту тему так как она нас очень заинтересовала тем , что геометрия Лобачевского очень полезна в современном мире, и мы хотим немного рассказать ...Весёлая геометрия
Пуст сегодня дворик наш, За окошком хмуро. Я взял фломастер, карандаш, Решил чертить фигуры. Передо мной бумаги лист, До чего ж он бел и чист. Фломастером ...Конспекты
Геометрическое решение негеометрических задач
Урок по теме:. «Геометрическое решение негеометрических задач». Сивак Светлана Олеговна. учитель математики. высшей категории. Гимназии №56. ...Геометрическое применение производной
Тема «Геометрическое применение производной». Производная функции y = y(x) при данном значении аргумента х = х. 0. равна угловому коэффициенту касательной, ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:14 апреля 2019
Категория:Математика
Содержит:34 слайд(ов)
Поделись с друзьями:
Скачать презентацию