Презентация "Симметрия в окружающем мире" по математике – проект, доклад
Презентацию на тему "Симметрия в окружающем мире" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 17 слайд(ов).
Слайды презентации
Список похожих презентаций
"Симметрия в архитектуре Старого Оскола"
Остановка 1. Главная улица города – улица Ленина. Мы находимся в центре нашего города у здания администрации. Какие приемы использовал архитектор, ...В мире чисел
Корни нумерологии. 1. Качества: благость, желательность, необходимость, неделимость. Связывалась с Аполлоном, Прометеем Символизирует начинание, источник, ...В мире числовых суеверий
Я выросла в потомственной семье математиков. Мои бабушка, Елисеева Ольга Алексеевна – заслуженный учитель РФ, и дедушка, Елисеев Николай Александрович, ...В мире чисел. ВАЖНАЯ ЦИФРА.
Жили – были числа. Назови их…. А какие числа стояли не на своих местах? Числа очень любили складываться, потому что они сразу превращались в большее ...В мире плоскостей
1. Изображение. . . . Сколько тут элементов? «Невозможные объекты» и зрительные иллюзии. Бесконечная фотография. Невозможное окно. Сколько здесь колонн? ...«Симметрия в пространстве» геометрия
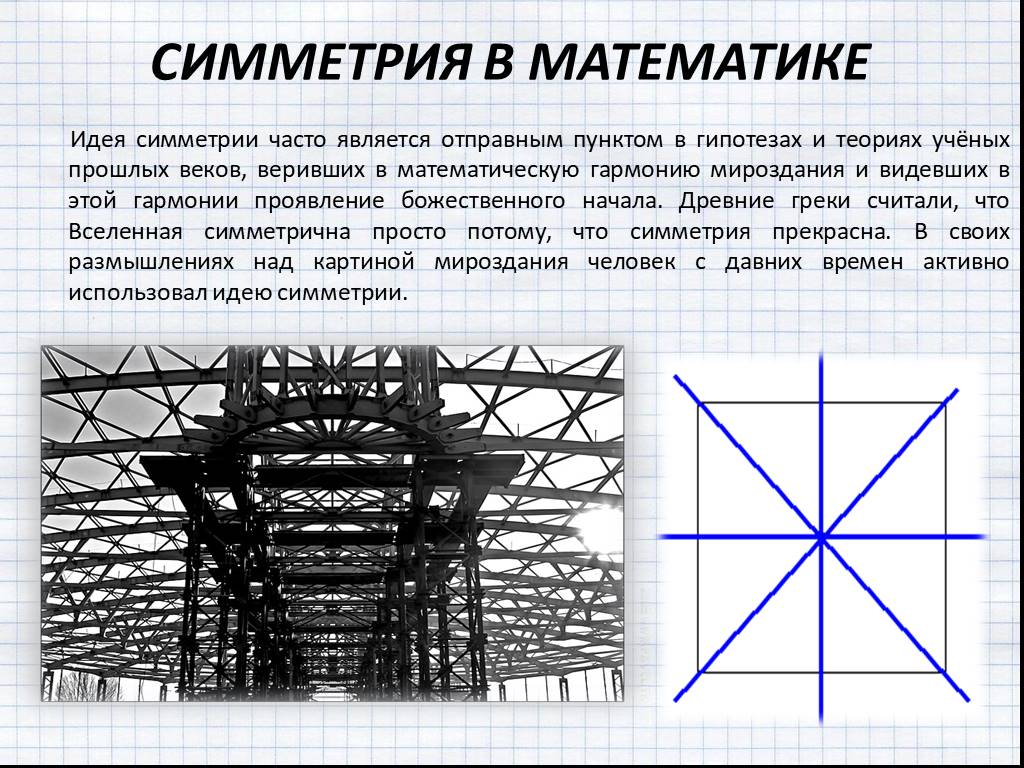
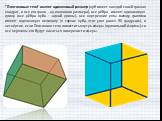
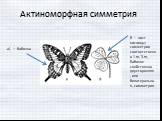
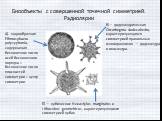
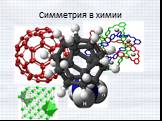
Что такое симметрия? Симметрия в переводе с греческого означает соразмерность. Под симметрией принято понимать свойство геометрической фигуры, расположенной ...В мире чисел
Математика — это наука, имеющая дело с числами, количеством, формой. Без знания математики вся современная жизнь была бы невозможна. Например, у нас ...В мире единиц длины
Как люди измеряли длину раньше и как измеряют теперь? Историческая справка. С незапамятных времён человеку приходилось измерять расстояние в связи ...«В мире животных. Занимательная математика»
Цели:. Знать: алгоритмы сравнения, сложения, вычитания десятичных дробей, названия геометрических фигур; правила правописания числительных. Уметь: ...В мире квадратных уравнений
Оглавление. Введение Заметки прошлого Основные понятия Теорема Виета Способы решения квадратного уравнения. Математика — основа точных наук. На первый ...Бумажные складные модели и их использование на уроках геометрии в 10 классе
Модель 1 – «Две пересекающиеся плоскости». Согнутый пополам лист бумаги служит моделью двух пересекающихся плоскостей. Линия сгиба – прямая их пересечения. ...Больше в несколько раз, меньше в несколько раз
ЦЕЛЬ УРОКА. раскрытие смысла слов “больше (меньше) в несколько раз”. Расположите числа в порядке возрастания. 18, 9, 45, 27, 36, 72, 54, 63, 9, 18, ...Биссектриса угла в треугольнике
Задачи УЧЕБНИК А О В С D 80º ? 180º- 80º= 100º 100º Ответ:155º, 25º, 155º. Задача №535 биссектриса ? Определение. Биссектриса угла – это луч с началом ...Биография М.В. Ломоносова в цифрах
=2 =0,3 =3,6 =0,04 =1 =0,8 =0,42 =21,2 М И Ш А Н С К О Е. Ломоносов Родился в с. Мишанинском Архангельской губернии. 8 ноября 1711. Длина = 15,5 м ...Бийская крепость в цифрах и фактах
Бийская крепость в цифрах и фактах. Цели урока:. Познакомиться с историей возникновения родного города Научиться определять временные промежутки и ...Без математики, друзья, в жизни нам никак нельзя
Актуальность. Математика находится в тесной связи со всеми естественными, гуманитарными, точными науками и др., математические знания применяются ...Арифметические операции в позиционных системах счисления
Ответьте на вопросы:. Какие системы называются НЕПОЗИЦИОННЫМИ? Какие системы называются ПОЗИЦИОННЫМИ? Какое число называют – ОСНОВАНИЕ позиционной ...«Математика в профессиях»
Ознакомление с типами профессий и характеристиками труда. Исследование значения математики в различных областях деятельности человека. Развитие познавательной ...Арифметическая прогрессия в древности
Египетские папирусы и вавилонские клинописные таблички, относящие ко II тыс. до н.э., содержат примеры задач на арифметическую прогрессию. Каких-либо ...Арифметическая и геометрическая прогрессии в заданиях ГИА
Цели урока: Обобщить и систематизировать знания учащихся по данной теме. Разобрать типичные задания встречающихся в сборниках для подготовки к ГИА. ...Конспекты
Видеть и слышать, или как не потеряться в мире информации
Конспект – сценарий урока, разработанного учителями МОУ Брызгаловская СОШ Ивановой Е.Б. и Колпаковой Л.В. Тема: «Видеть и слышать, или как не потеряться ...В мире формул
Тема: «В мире формул». . 7 класс. Цели урока:. . Обучающая:. обобщить изученный материал, проверить степень усвоения темы; продолжить преобразовывать ...В мире многоугольников
Технологическая карта урока. Учитель: Береговская Е.А. Предмет: математика. Класс: 5 –б. Автор УМК: Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. ...В мире симметрии
В мире симметрии. Цели:. Обучающая. Сформировать понятие симметрии, как геометрическое свойство фигур. Развивающая. . Продолжить формирование ...В мире желтого цвета
Конспект урока для 1 класса на тему. «В мире желтого цвета». Программное содержание. Учить детей называть основные цвета спектра: желтый, ...В мире Математики
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ. . Дополнительного образования детей Центр детского Творчества. Разработка занятия ...В мире волшебных чисел
Конспект занятия по математике в старшей группе. . . Тема:. "В мире волшебных чисел". Выполнила воспитатель старшей группы:. Куликова ...В мире десятичных дробей
МКУ «Департамент образования Местной администрации г.о. Нальчик». Муниципальное казенное образовательное учреждение. дополнительного образования ...Виды углов в планиметрии
Лабораторно-практические занятия по геометрии в 7 классе. Лабораторно-практические занятия имеют важное значение, особенно при обучении детей с ...Введение в теорию вероятностей
9 класс. Тема: Введение в теорию вероятностей.(90 мин.). Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 февраля 2019
Категория:Математика
Содержит:17 слайд(ов)
Поделись с друзьями:
Скачать презентацию