Презентация "Векторы" (8 класс) по математике – проект, доклад
Презентацию на тему "Векторы" (8 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 16 слайд(ов).
Слайды презентации
Список похожих презентаций
Векторы геометрия
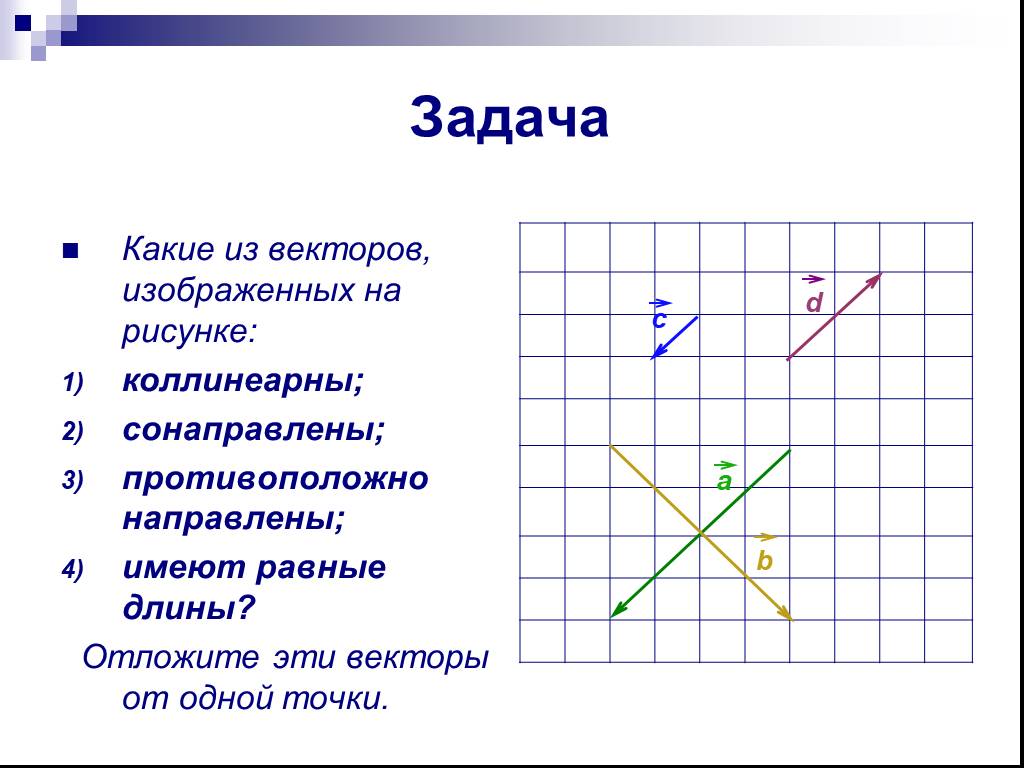
Вектора. Действия с векторами. а b. Сумма векторов. Вырази вектор АС АN AM CB CM. Произведение векторов. Выразите вектор ОМ. М – точка пересечения ...Векторы в пространстве
ВЕКТОРЫ. Назад. СУММА И РАЗНОСТЬ ВЕКТОРОВ. ЗАКОНЫ СЛОЖЕНИЯ ВЕКТОРОВ. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО. . . КОМПЛАНАРНЫЕ ВЕКТОРЫ. ПРАВИЛО ПАРАЛЛЕЛЕПИПЕДА. ...Векторы в пространстве Геометрия
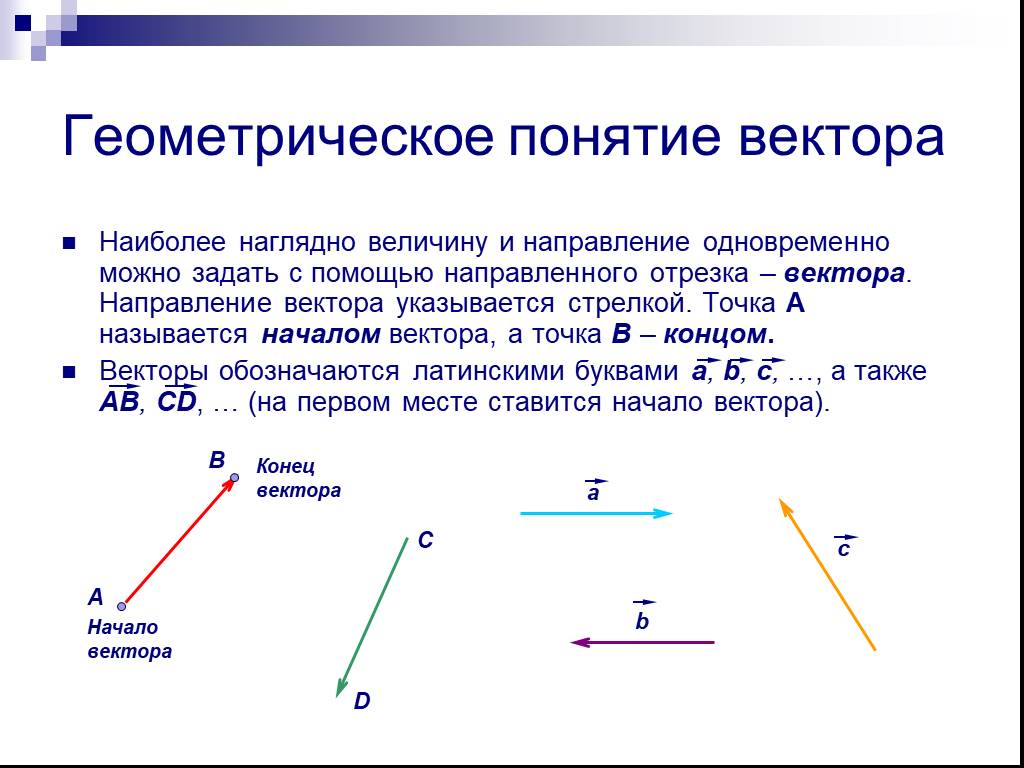
В Е К Т О Р. - это направленный отрезок. Начало вектора Конец вектора а. КОЛЛИНЕАРНЫЕ ВЕКТОРЫ. - это векторы, лежащие на одной или на параллельных ...Векторы в пространстве
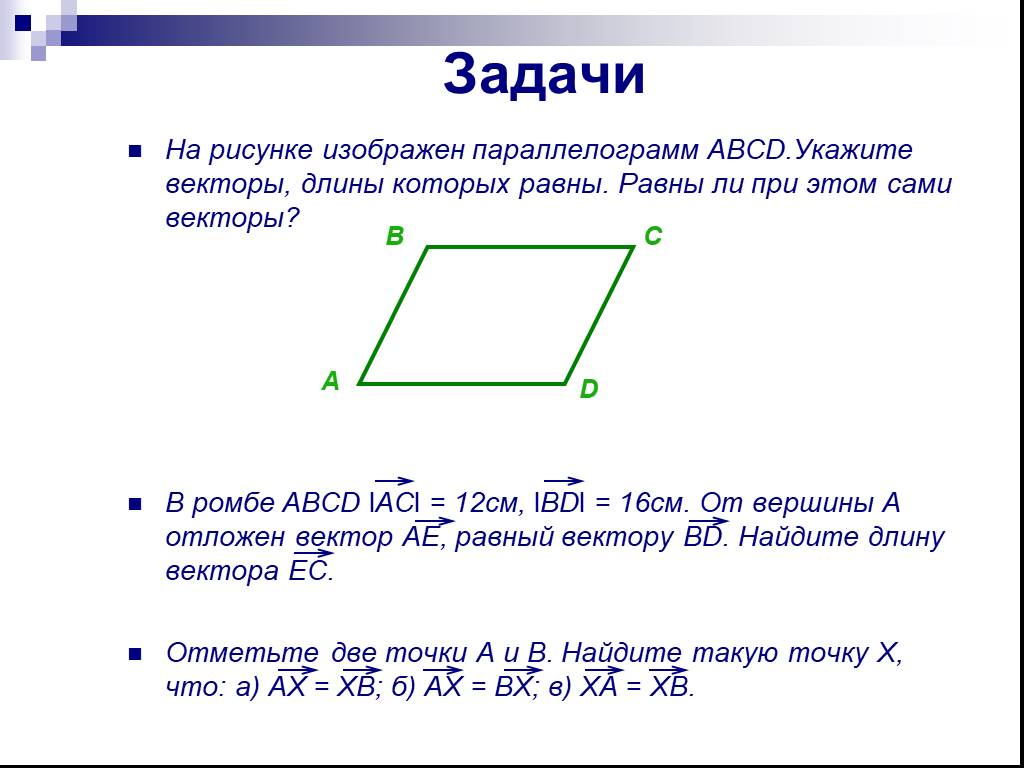
Понятие вектора в пространстве. Понятие вектора. Равенство векторов 1. Вектор – направленный отрезок 2. Длина вектора – длина отрезка. АВ СЕ Р АВ ...Векторы в пространстве
Цели урока. Знать: определение вектора в пространстве и связанные с ним понятия; равенство векторов. Уметь: решать задачи по данной теме. Физические ...Векторы в пространстве
В Е К Т О Р. - это направленный отрезок. Начало вектора Конец вектора а. КОЛЛИНЕАРНЫЕ ВЕКТОРЫ. - это векторы, лежащие на одной или на параллельных ...Векторы в пространстве
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат OX и OY. Оси координат пересекаются в точке ...Векторы
. . НАЧАЛО КОНЕЦ А В ВЕКТОР ВЕКТОР —. это направленный отрезок, для которого указаны, какая точка считается началом, а какая концом. . КОЛЛИНЕАРНЫЕ ...Векторы
Вектором называется направленный отрезок. Модулем вектора называется длина содержащего его отрезка. l AB l=AB. Ненулевые векторы называются коллинеарными, ...Векторы
Мой первый слог – почтенный срок, Коль прожит он недаром. Модель второго – на столе, Румяна, с пылу, с жару. Меня вы встретите везде – Такой я вездесущий. ...Векторы
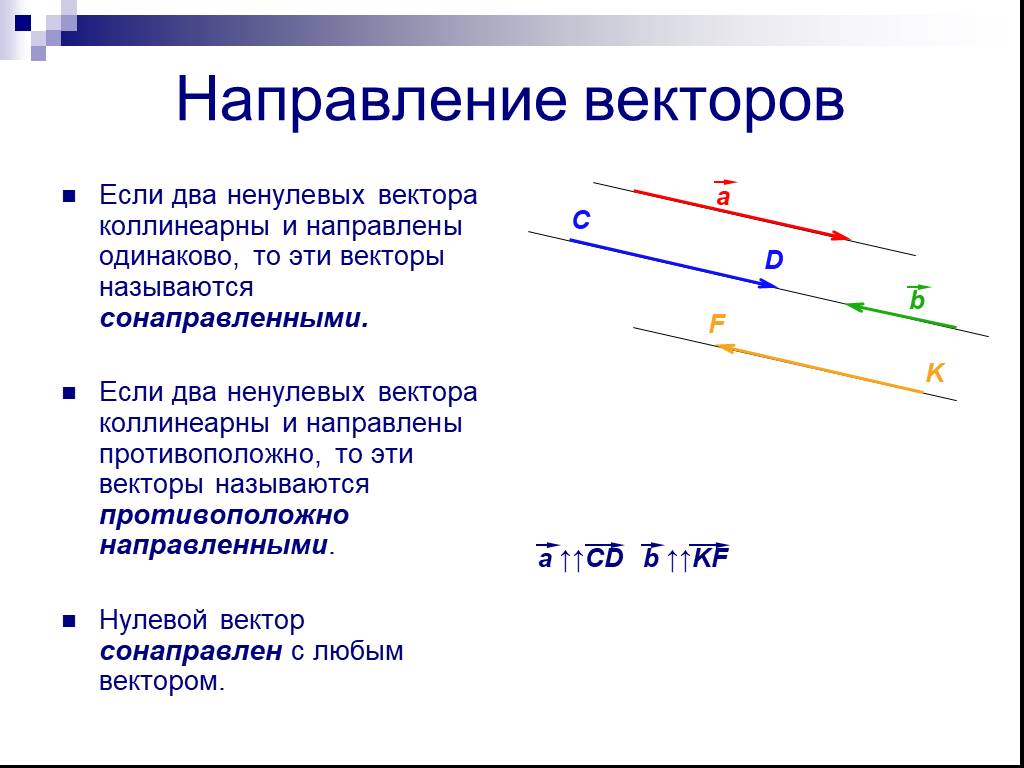
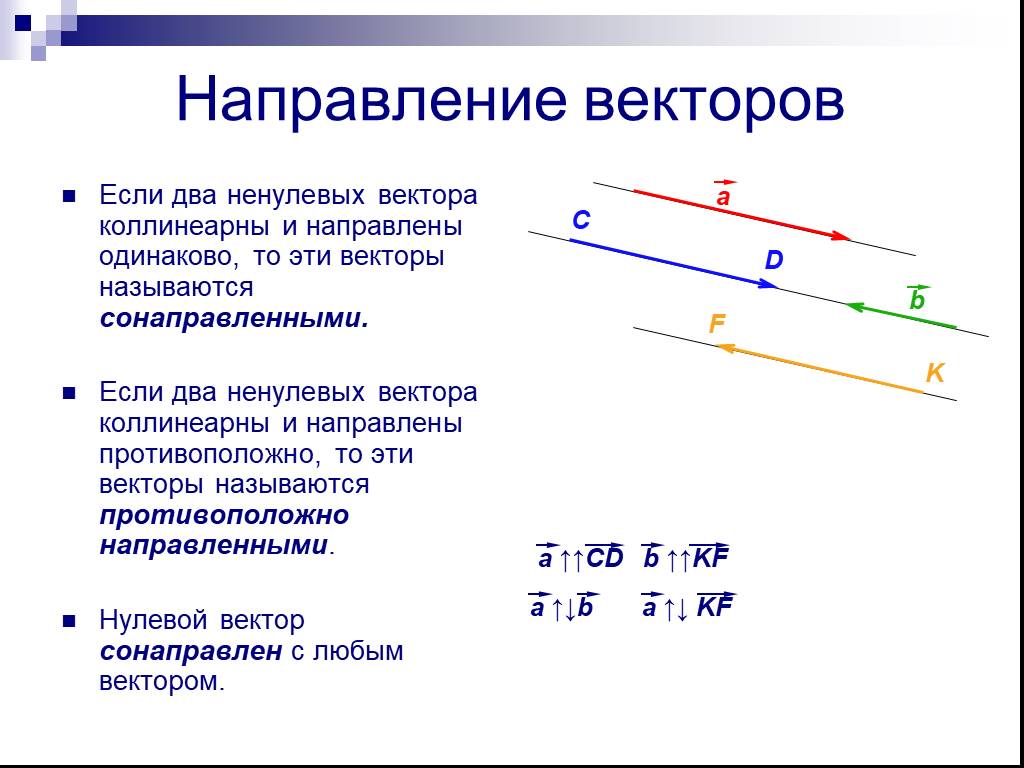
Равные векторы одинаково направлены и равны по абсолютной величине. Равные векторы имеют равные соответствующие координаты. Равенство векторов. а ...Векторы
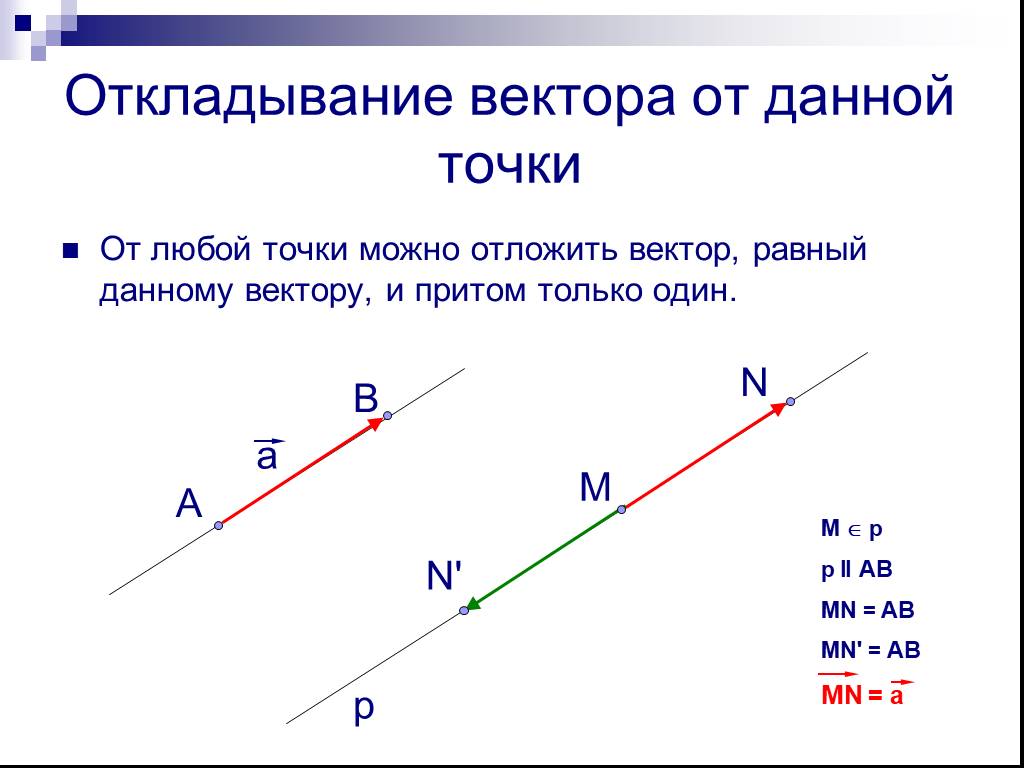
От любой точки можно отложить вектор равный данному , притом только один . g f M B. Откладывание векторов от данной точки. f = g. a h n. Векторы называются ...Векторы
«Векторы на плоскости» (геометрия 9 класс). Цели: обобщить и систематизировать материал по теме «Векторы» проверить знания основных понятий и формул ...Векторы
Девиз урока:. Что только слышу - забываю! Что слышу и вижу - вспоминаю! Что слышу, вижу и спрашиваю – начинаю понимать! Что слышу, вижу, спрашиваю ...Векторы на плоскости
Аналитическая геометрия. Алгебраические поверхности и линии на плоскости первого порядка. Опр. Геометрическое место точек в пространстве (на плоскости) ...Преобразования фигур. Движение. Векторы, действия с векторами
Преобразования фигур. Движение. Уроки геометрии в 8 классе. А В С. Преобразование одной фигуры в другую, при котором сохраняется расстояние между ..."Векторы в пространстве"
Векторы в пространстве. Тема урока:. ТАБЛИЦА «Векторы в пространстве». ФИЗИКА. Направление движения тела. ЭЛЕКТРОТЕХНИКА. Движение заряженных частиц ...Векторы
А В С. K M N P. Коллинеарные вектора. Коллинеарные векторы. Длина (модуль) вектора. АВ=15 см М. Векторы называются равными, если они сонаправлены ...Куда пропала математика?
Замочек №1. Задача 1. Часто знает и дошкольник, Что такое треугольник. А уж вам-то как не знать! Но совсем другое дело: Очень быстро и умело Треугольники ...Интересная математика
Франция Герб Франции Флаг Франции. . Страна граничит с 8 странами: Италией, Испанией, Бельгией, Люксембургом, Германией, Швейцарией, Монако и Андоррой. ...Конспекты
Векторы на плоскости
. Конспект. обобщающего урока по теме «Векторы на плоскости». . (геометрия 9 класс). Тема. Систематизация и обобщение изученного материала ...Векторы
. Академия АйТи. ИТОГОВАЯ РАБОТА. по программе:. «Применение международных информационных технологий: применение ИКТ в учебном процессе». ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 января 2019
Категория:Математика
Классы:
Содержит:16 слайд(ов)
Поделись с друзьями:
Скачать презентацию