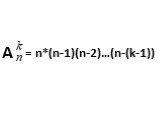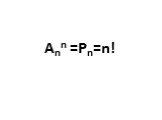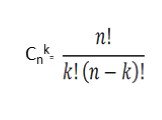Презентация "КОМБИНАТОРИКА. КОМБИНАТОРНЫЕ ЗАДАЧИ" по математике – проект, доклад
Презентацию на тему "КОМБИНАТОРИКА. КОМБИНАТОРНЫЕ ЗАДАЧИ" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 52 слайд(ов).
Слайды презентации
Список похожих презентаций
ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ПРОИЗВОДНОЙ
Дидактические цели проекта:. формирование предметной компетентности - самостоятельной познавательной активности, навыков работы с большими объемами ...ЗАДАЧИ НА ПОСТРОЕНИЕ
Дано: № 313 Построить:. ∆ ABC, где BD - медиана. Анализ: A B C D B1. Описание построения:. 1. Строим ∆BCB1 по трём сторонам (BB1 = 2BD, CB1 = AB). ...ЗАДАЧИ НА ЧАСТИ
Математика - это язык, на котором говорят все точные науки. Н.И. Лобачевский. Как бы машина хорошо ни работала, она может решать все требуемые от ...ЗАДАЧИ НА ДРОБИ
Типы задач. Нахождение дроби от числа Нахождение неизвестного числа по значению его дроби Какую часть составляет одно число от другого? Нахождение ...Конспекты
КОМБИНАТОРНЫЕ ЗАДАЧИ
. МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ. . КУЙБЫШЕВСКОГО РАЙОНА «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №2». ...УЧИМСЯ РЕШАТЬ ЗАДАЧИ
УЧИМСЯ РЕШАТЬ ЗАДАЧИ. Подготовила:. Ботвинова Элина Юрьевна. Учитель начальных классов МБОУ №СОШ№1» г. Барнаул. Описание:. урок математики ...РЕШАЕМ ЗАДАЧИ
муниципальное общеобразовательное учреждение. Дмитровская средняя общеобразовательная школа № 1 им. В.И. Кузнецова. г. Дмитрова Московской области. ...ПРОЦЕНТЫ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ
Открытый урок. подготовки к ГИА по математике в 9 классе. Тема:. . ПроцентыОсновные задачи на проценты. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:24 декабря 2012
Категория:Математика
Автор презентации:Минасян Л.Г.
Содержит:52 слайд(ов)
Поделись с друзьями:
Скачать презентацию