Презентация "Формализация и алгоритмизация процесса функционирования систем" по экономике – проект, доклад

Тема 3. Формализация и алгоритмизация процесса функционирования систем

Дисциплина «Имитационное моделирование экономических процессов» Специальность №08080165 «Прикладная информатика (в экономике)» Институт информатики, инноваций и бизнес систем Кафедра информатики, инженерной и компьютерной графики Старший преподаватель Кийкова Е.В.

СОДЕРЖАНИЕ

Ключевые понятия Учебный материал Вопросы для самопроверки Рекомендуемая литература

КЛЮЧЕВЫЕ ПОНЯТИЯ

Концептуальная модель Модель рабочей нагрузки Равномерный отсчет времени Событийный отсчёт времени Реальное время Модельное время Машинное время Виды параллельных процессов Список текущих событий Список будущих событий Список прерываний План проведения экспериментов Калибровка модели

УЧЕБНЫЙ МАТЕРИАЛ

Основные задачи лекции

Рассмотреть этапы моделирования систем. Рассмотреть принципы организации отсчета времени в модели и представления параллельно развивающихся процессов. Получение и интерпретация результатов моделирования.

Основные этапы процесса моделирования Формулировка проблемы. 2. Построение математической модели. 3. Алгоритмизация модели и ее машинная реализация. 4. Получение и интерпретация результатов моделирования.

1. Формулировка проблемы На первом этапе моделирования выполняются: Формулировка задачи и планирование исследования системы. Сбор данных и определение модели. Определение адекватности концептуальной модели.

Решаются следующие вопросы: глобальная цель исследования; специальные вопросы, на которые должно ответить исследование; критерии качества работы, используемые в будущем для оценки эффективности различных конфигураций системы; масштаб модели; моделируемые конфигурации системы; применяемое программное обеспечение; временной интервал для исследования и необходимые ресурсы.

Сбор данных и определение модели включают: сбор информации о конфигурации системы и способах эксплуатации; сбор данных для определения параметров модели и входных распределений вероятностей; схематическое изображение данных – концептуальная модель; сбор данных о рабочих характеристиках существующей системы; выбор уровня детальности модели; установление между каждым элементом модели и соответствующим ему элементом системы взаимно-однозначного соответствия; регулярное взаимодействие с руководителем и другими ведущими специалистами проекта.

Общая цель моделирования – это определение (расчет) значений выбранного показателя эффективности для различных стратегий проведения эксперимента (или вариантов реализации проектируемой системы).

Концептуальная (содержательная) модель – это абстрактная модель, определяющая структуру моделируемой системы, свойства её элементов и причинно-следственные связи, присущие системе и существенные для достижения цели моделирования.

Построение концептуальной модели включает следующие этапы: определение типа системы; описание рабочей нагрузки; декомпозицию системы.

. Рабочая нагрузка – это совокупность внешних воздействий, оказывающих влияние на эффективность применения данной системы в рамках проводимой операции. Модель рабочей нагрузки должна обладать следующими основными свойствами: совместимостью с моделью системы; представительностью; управляемостью; системной независимостью.

Свойство совместимости предполагает, что: степень детализации описания рабочей нагрузки соответствует детализации описания системы; модель рабочей нагрузки должна быть сформулирована в тех же категориях предметной области, что и модель системы.

Представительность модели рабочей нагрузки определяется её способностью адекватно представить рабочую нагрузку в соответствии с целями исследования, т.е. модель рабочей нагрузки должна отвечать целям исследования системы. Под управляемостью понимается возможность изменения параметров модели рабочей нагрузки в диапазоне, определяемом целями исследования.

Системная независимость – это возможность переноса модели рабочей нагрузки с одной системы на другую с сохранением её представительности.

Декомпозиция системы производится исходя из выбранного уровня детализации модели, который, в свою очередь, определяется тремя факторами: целями моделирования; объёмом априорной информации о системе; требованиями к точности и достоверности результатов моделирования.

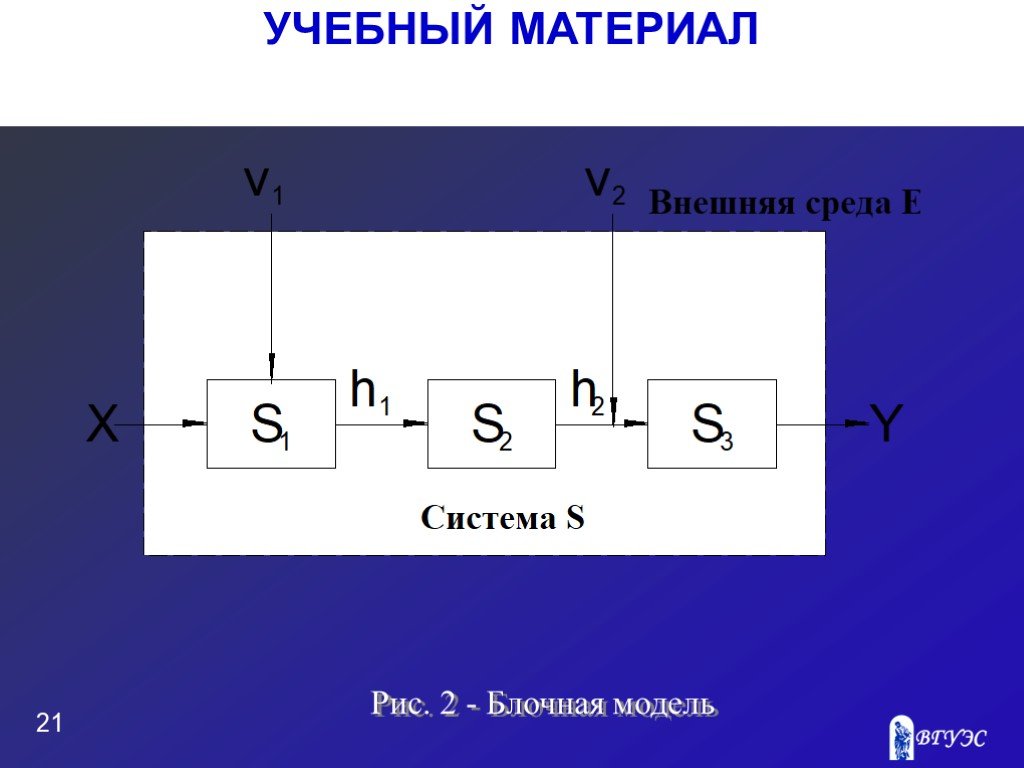
2. Построение математической модели Математическая модель строится по блочному принципу. При этом могут быть выделены три автономные группы блоков такой модели: 1. Блоки первой группы имитируют воздействие внешней среды E на систему S. 2. Блоки второй группы являются собственно моделью процессов функционирования исследуемой системы S. 3. Блоки третьей группы являются вспомогательными и служат для машинной реализации блоков двух первых групп, а также для фиксации и обработки результатов моделирования.

Построение математической модели

Рис. 1 - Концептуальная модель

В ходе анализа концептуальной модели группируем элементы системы в зависимости от их функций и целей моделирования. Элементы 2-4, 22, 24-31 являются второстепенными, т. к. они не оказывают существенного влияния на ход процессов, исследуемых с помощью модели, поэтому в модель эти элементы не включаются. 2. Элементы 8, 16, 23 заменяются пассивными связями h1, отражающими внутренние свойства системы. 3. Некоторая часть элементов 1, 6, 14 - заменяются входными факторами Х и воздействиями внешней среды V1.

4. Возможны и комбинированные замены: элементы 5, 11, 19 - заменены пассивной связью h2 и воздействием внешней среды V2. 5. Элементы 13, 21 - отражают воздействие системы на внешнюю среду Y. 6. Оставшиеся элементы системы группируются в блоки S1, S2, S3 - отражающие процесс функционирования исследуемой системы. Каждый из этих блоков достаточно автономен.

Рис. 2 - Блочная модель

Математической моделью процесса может служить система соотношений вида: Теперь нужно подобрать типовые математические модели (Р-схемы, Q-схемы, D-схемы и т.д.), которые достаточно точно описывают основные особенности реальных явлений исследуемой модели.

3. Алгоритмизация модели и ее машинная реализация Перед исследователем стоит две задачи: Организация отсчета времени в модели и представление параллельно развивающихся процессов. 2. Отображение моделируемой системы в виде алгоритмов и программ.

При разработке практически любой имитационной модели и планировании проведения модельных экспериментов необходимо соотносить между собой три представления времени: реальное время, в котором происходит функционирование имитируемой системы; модельное (системное) время, в масштабе которого организуется работа модели; машинное время, отражающее затраты времени ЭВМ на проведение имитации.

С помощью механизма модельного времени решаются следующие задачи: отображается переход моделируемой системы из одного состояния в другое; производится синхронизация работы компонент модели; изменяется масштаб времени «жизни» (функционирования) исследуемой системы; производится управление ходом модельного эксперимента; моделируется квазипараллельная реализация событий в модели.

Существует два способа изменения модельного времени: с постоянным шагом и по особым состояниям. Выбор метода отсчета модельного времени зависит от назначения модели, её сложности, характера исследуемых процессов, требуемой точности результатов и т.д.

Равномерный отсчет времени (РОВ) называется "принцип ". Модельное время изменяется с равномерным шагом , т.е. , , . Этот метод целесообразно использовать если: события появляются регулярно, их распределение во времени достаточно равномерно; число событий велико и моменты их появления близки; невозможно заранее определить моменты появления событий.

Универсальной методики выбора величины шага моделирования ( ) не существует, но во многих случаях можно использовать один из следующих подходов: принимать величину шага равной средней интенсивности возникновения событий различных типов; выбирать величину равной среднему интервалу между наиболее частыми (или наиболее важными) событиями. Этот принцип не очень хорош для дискретных систем (из-за его непрерывности).

Событийный отсчет времени - "принцип особых состояний". Системное время изменяется со случайным шагом, который определяется временем наступления очередного события. Если известен закон распределения интервалов между событиями, то к текущему значению модельного времени добавляется величина интервала, полученная с помощью соответствующего датчика. Если же момент наступления события определяется некоторыми логическими условиями, то необходимо сформулировать эти условия и проверить их истинность для каждого последующего шага моделирования.

Моделирование по особым состояниям целесообразно использовать если: события распределяются во времени не равномерно или интервалы между ними велики; предъявляются повышенные требования к точности определения взаимного положения событий во времени; необходимо учитывать наличие одновременных событий. Достоинство метода – что он позволяет экономить машинное время, особенно при моделировании систем периодического действия, в которых события длительное время могут не наступать.

Практически любая более или менее сложная система имеет в своем составе компоненты, работающие одновременно (параллельно). Параллельно работающие подсистемы могут взаимодействовать самым различным образом либо вообще работать независимо друг от друга. Способ взаимодействия подсистем определяет вид параллельных процессов, протекающих в системе. В свою очередь, вид моделируемых процессов влияет на выбор метода их имитации.

Виды параллельных процессов: Асинхронный параллельный процесс – такой процесс, состояние которого не зависит от состояния другого параллельного процесса (ПП). Синхронный параллельный процесс – состояние которого зависит от состояния взаимодействующих с ним ПП. Один и тот же процесс может быть синхронным по отношению к одному из активных ПП и асинхронным по отношению к др. Независимый ПП – процесс, который не является подчиненным ни для одного из процессов. Подчиненный ПП – создается и управляется другим процессом (более высокого уровня).

На прикладном уровне взаимодействие между ПП реализуется программистом средствами языка, на котором разрабатывается программное обеспечение. Наибольшими возможностями в этом отношении обладают языки реального времени и языки моделирования. Рассмотрим механизм реализации ПП на примере транзактных систем моделирования. Под событием понимается любое перемещение транзакта по системе, а также изменение его состояния (обслуживается, заблокирован и т. д.).

Событие связанное с транзактом может храниться а одном из следующих списков: 1. Список текущих событий – в этом списке находятся события, время наступления которых меньше или равно текущему модельному времени. События с «меньшим» временем связаны с перемещением тех транзактов, которые должны были начать двигаться, но были заблокированы.

2. Список будущих событий – этот список содержит события, время наступления которых больше текущего модельного времени, т. е. События, которые должны произойти в будущем (условия наступления которых уже определены – например, известно, что транзакт будет обслуживаться некоторым устройством 10 ед. времени). 3. Список прерываний – данный список содержит события, связанные с возобновлением обработки прерванных транзактов. События из этого списка выбираются в том случае, если сняты условия прерывания.

Удобной формой представления логической структуры моделей процессов функционирования систем является схема. На различных этапах моделирования составляются обобщенные, детальные, логические схемы, а так же схемы программ. Обобщенная (укрупненная) схема моделирующего алгоритма - задает общий порядок действий при моделировании системы без каких-либо уточняющих деталей. Обобщенная схема показывает, что необходимо выполнить на очередном шаге моделирования.

Детальная схема моделирующего алгоритма содержит уточнения, отсутствующие в обобщенной схеме. Детальная схема показывает не только, что следует выполнять на очередном шаге моделирования системы, но и как это выполнить. Логическая схема моделирующего алгоритма - представляет собой логическую модель процесса функционирования системы S. Логическая схема показывает упорядоченную во времени последовательность логических операций, связанных с решением задачи моделирования.

Схема программы отображает порядок программной реализации моделирующего алгоритма с использованием конкретного математического обеспечения.

4. Получение и интерпретация результатов моделирования Перед проведением рабочих расчетов на ПЭВМ должен быть составлен план проведения эксперимента с моделью системы S с указанием комбинаций переменных и параметров, для которых проводится моделирование. Планирование модельных экспериментов преследует две основные цели: сокращение общего объема испытаний при соблюдении требований к достоверности и точности их результатов; повышение информативности каждого из экспериментов в отдельности.

Существует два основных варианта постановки задачи планирования имитационного эксперимента: из всех допустимых выбрать такой план, который позволил бы получить наиболее достоверное значение функции отклика при фиксированном числе опытов; выбрать такой допустимый план, при котором статистическая оценка функции отклика может быть получена с заданной точностью при минимальном объеме испытаний. Первый вариант называется стратегическим планированием, второй – тактическим.

Решения, принимаемые исследователем по результатам имитационного моделирования, могут быть конструктивными только при выполнении двух основных условий: полученные результаты обладают требуемой точностью и достоверностью; исследователь способен правильно интерпретировать полученные результаты и знает, каким образом они могут быть использованы.

Точность моделирования определяется несколькими факторами: выбором единицы измерения времени; количеством реализаций или длительностью моделирования для стационарных систем; начальным состоянием системы.

При имитационном моделировании на достоверность результатов влияет ряд факторов, основными из которых являются: моделирование случайных факторов, основанное на использовании датчиков случайных чисел, которые могут вносить «искажения» в поведение модели; наличие нестационарного режима работы модели: использование нескольких разнотипных математических методов в рамках одной модели: зависимость результатов моделирования от плана эксперимента: необходимость синхронизации работы отдельных компонентов модели.

Пригодность имитационной модели для решения задач исследования характеризуется тем, в какой степени она обладает так называемыми целевыми свойствами. Основными из них являются: адекватность; устойчивость; чувствительность.

В общем случае под адекватностью понимают степень соответствия модели тому реальному явлению или объекту, для описания которого она строится. Для проектируемых систем адекватность модели определяется степенью её соответствия целям исследования.

Процедура оценки адекватности основана на сравнении измерений на реальной системе и результатов экспериментов на модели и может проводиться различными способами. Наиболее распространенные из них: по средним значениям откликов модели и системы; по дисперсиям отклонений откликов модели от среднего значения откликов системы; по максимальному значению относительных отклонений откликов модели от откликов системы.

Для проектируемой системы оценка адекватности программно-реализованной модели заключается в проверке того, насколько корректно она отражает концептуальную модель.

Устойчивость модели – это её способность сохранять адекватность при исследовании эффективности системы на всем возможном диапазоне рабочей нагрузки, а также при внесении изменений в конфигурацию системы. В общем случае можно утверждать, что чем ближе структура модели структуре системы и чем выше степень детализации, тем устойчивее модель. Устойчивость результатов моделирования может быть оценена методами математической статистики.

Оценка чувствительности модели к изменению параметров рабочей нагрузки и внутренних параметров самой системы проводится для каждого параметра в отдельности. Данные, полученные при оценке чувствительности модели, могут быть использованы при планировании экспериментов: большее внимание должно уделяться тем параметрам, по которым модель является более чувствительной.

Если в результате проведенной оценки качества модели оказалось, что её целевые свойства не удовлетворяют разработчика, необходимо выполнить её калибровку, т.е. коррекцию с целью приведения в соответствие предъявляемым требованиям.

Процесс калибровки носит итеративный характер и состоит из трех основных этапов: Глобальные изменения модели (например, введение новых процессов, изменение типов событий и т.д.). Локальные изменения (в частности, изменение некоторых законов распределения моделируемых случайных величин). Изменение специальных параметров, называемых калибровочными.

Для правильной интерпретации данных должен быть произведен предварительный анализ на первых этапах создания модели. Планирование машинного эксперимента позволяет вывести необходимое количество выходных данных и определить метод их анализа. При этом необходимо выводить только те результаты, которые нужны для проведения дальнейшего анализа. Необходимо решить вопрос о форме представления результатов моделирования (таблицы, графики, диаграммы, гистограммы, схемы и т.п.).

В выводах по результатам моделирования необходимо указать, какими средствами и какой ценой достигается сформулированная цель исследования.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

Перечислите этапы моделирования. Дайте определение понятиям: концептуальная модель, модель рабочей нагрузки. Дайте определение понятиям: реальное время, модельное время, машинное время. Перечислите способы изменения модельного времени. Перечислите виды параллельных процессов. Дайте определение понятиям: адекватность, устойчивость, чувствительность. Этапы процесса калибровки модели.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Гультяев А.К. Имитационное моделирование в среде Windos. – СПб.: КОРОНА принт, 2001. – 400 с. Кийкова Е.В., Лаврушина Е.Г. Имитационное моделирование экономических процессов. Учебное пособие.- Владивосток: ВГУЭС, 2007. -128 с. Советов Б.Я., Яковлев С.А. Моделирование систем. Учебник для ВУЗов. - М.: Высшая школа, 2001.-344 с.

Использование материалов презентации Использование данной презентации, может осуществляться только при условии соблюдения требований законов РФ об авторском праве и интеллектуальной собственности, а также с учетом требований настоящего Заявления. Презентация является собственностью авторов. Разрешается распечатывать копию любой части презентации для личного некоммерческого использования, однако не допускается распечатывать какую-либо часть презентации с любой иной целью или по каким-либо причинам вносить изменения в любую часть презентации. Использование любой части презентации в другом произведении, как в печатной, электронной, так и иной форме, а также использование любой части презентации в другой презентации посредством ссылки или иным образом допускается только после получения письменного согласия авторов.