Презентация "Метод статистического моделирования" по экономике – проект, доклад

Тема 4. Метод статистического моделирования

Дисциплина «Имитационное моделирование экономических процессов» Специальность №08080165 «Прикладная информатика (в экономике)» Институт информатики, инноваций и бизнес систем Кафедра информатики, инженерной и компьютерной графики Старший преподаватель Кийкова Е.В.

СОДЕРЖАНИЕ

Ключевые понятия Учебный материал Вопросы для самопроверки Рекомендуемая литература

КЛЮЧЕВЫЕ ПОНЯТИЯ

Метод Монте-Карло Случайная величина Базовая случайная величина Псевдослучайные числа Мультипликативный метод Смешанный метод Метод серединных квадратов Длина отрезка апериодичности Эмпирические тесты Теоретические тесты

УЧЕБНЫЙ МАТЕРИАЛ

Основные задачи лекции

Раскрыть основные понятия, связанные с методом статистического моделирования. Рассмотреть способы формирования случайных величин. Рассмотреть способы проверки качества последовательностей псевдослучайных чисел.

На этапе исследования и проектирования систем при построении и реализации машинных моделей широко используется метод статистических испытаний (метод Монте-Карло), который базируется на использовании случайных чисел. Метод статистических испытаний – это метод решения невероятностной проблемы вероятностным способом. Явное представление времени здесь отсутствует. Суть метода в том, что процесс описывают формулами и логическими выражениями на ЭВМ. Затем в модель вводят случайно изменяющиеся факторы и оценивают их влияние на показатели процесса. Результаты оценки подвергают статистической обработке.

В настоящее время моделирование по методу Монте-Карло широко применяется при решении определенных задач статистики, которые не поддаются аналитической обработке. Этот тип моделирования применялся для оценки критических значений или достоверности критерия при проверке гипотезы.

Общая структура статистической модели Задачи статистического моделирования: построение объекта моделирования; 2) формирование случайных взаимодействий; 3) организация статистической обработки данных моделирования; 4) задача планирования эксперимента.

Моделирование случайных процессов Имитационная модель позволяет исследовать поведение различных систем с учетом влияния случайных факторов. Эти факторы в зависимости от их природы могут быть отражены в модели как случайные события, случайные величины (дискретные или непрерывные) или как случайные функции (процессы).

К общим принципам имитации случайных воздействий на ЭВМ относятся: Формирование базовой случайной величины (CB) 2) Преобразование базовой случайной величины в значения случайных величин распределенных по требуемому закону.

Способы формирования базовой случайной величины В основе базовой СВ обычно используется СВ равномерно распределенная на интервале [0,1]. Рассмотрим общий случай распределения СВ на интервале [a,b]. Непрерывная СВ имеет равномерное распределение в интервале [a,b], если ее функции плотности (рис. 1) и распределения (рис. 2) соответственно примут вид:

. Рисунок 1 - Функция плотности для равномерного распределения Рисунок 2 - Функция равномерного распределения

Определим числовые характеристики случайной величины принимающей значения x: математическое ожидание (формула 1), дисперсию (формула 2) и среднее квадратическое отклонение (формула 3): (1) (2) (3)

При моделировании систем на ЭВМ приходится иметь дело со случайными числами интервала [0,1], когда границы интервала a=0, b=1. Рассмотрим частный случай равномерного распределения, когда функции плотности и распределения соответственно имеют вид:

Математическое ожидание такого распределения - , дисперсия - и среднеквадратическое отклонение - . Это распределение требуется получить на ЭВМ. Но получить его на цифровой ЭВМ невозможно, т.к. машина оперирует с n-разрядными числами. Поэтому на ЭВМ вместо непрерывной совокупности равномерных случайных чисел интервала [0,1] используют дискретную последовательность случайных чисел того же интервала. Закон распределения такой дискретной последовательности называют квазиравномерным распределением.

Получение квазиравномерных чисел Случайная величина, имеющая квазиравномерное распределение в интервале [0,1], принимает значения с вероятностями . Математическое ожидание и дисперсия квазиравномерной СВ соответственно имеют вид:

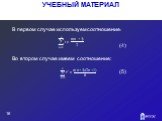
В первом случае используем соотношение: (4) Во втором случае имеем соотношение: (5)

Таким образом, математическое ожидание квазиравномерной случайной величины совпадает с математическим ожиданием равномерной случайной последовательности интервала [0,1], а дисперсия отличается множителем , который при достаточно больших близок к единице. На ЭВМ невозможно получить идеальную последовательность случайных чисел т.к. можно оперировать только с конечным множеством чисел, и для получения значений х случайной величины используют формулы; поэтому такие последовательности называют псевдослучайными.

Способы получения случайных чисел Моделирование любой системы или процесса, содержащих случайные компоненты, предполагает использование метода генерирования чисел, которые в определенном смысле являются случайными. Существуют два способа формирования случайных чисел (CЧ): с помощью специального физического датчика; 2) с помощью специальных программ.

Физический способ С распространением компьютеров (и моделирования) все более пристальное внимание стало уделяться методам генерирования, или генераторам, случайных чисел, совместимых со способом работы компьютеров. При этом способе генерации случайные числа вырабатываются специальной электронной приставкой - генератором (датчиком) СЧ, служащей в качестве одного из внешних устройств ЭВМ. В качестве физического эффекта, лежащего в основе таких генераторов чисел, чаще всего используются шумы в электронных и полупроводниковых приборах, явления распада радиоактивных элементов и т.д. (количество радиоактивных частиц).

Преимуществом физических датчиков является высокая скорость формирования случайных чисел. К недостаткам физических датчиков случайных чисел относятся: изготовление отдельного прибора; не позволяют гарантировать качество последовательности непосредственно во время моделирования системы на ЭВМ, а также повторно получать при моделировании одинаковые последовательности чисел.

Программный способ Наибольшее применение в практике моделирования на ЭВМ для генерации последовательностей псевдослучайных чисел получили алгоритмы вида: представляющие собой рекуррентные соотношения первого порядка, для которых начальное число x0 и постоянные параметры заданы.

Хороший арифметический генератор случайных чисел должен обладать следующими свойствами: Получаемые числа должны быть равномерно распределены в интервале [0,1] и не должны иметь корреляции друг с другом, в противном случае результаты моделирования могут оказаться полностью недействительными. 2. Чтобы генератор можно было использовать на практике, он должен обладать быстродействием и не требовать больших затрат памяти.

3. Генератор должен обеспечивать возможность точно воспроизводить заданный поток случайных чисел. 4. В генераторе должен быть предусмотрен простой способ получения отдельных потоков случайных чисел. Поток — это просто часть последовательности случайных чисел, производимых генератором, очередной поток начинается в том месте, где заканчивается предыдущий.

Метод серединных квадратов Алгоритм получения последовательности случайных чисел методом серединных квадратов сводится к следующему: Пусть имеется 2n- разрядное число, меньше 1: возведем его в квадрат: , а затем возьмем средние разрядов: , которые и будут очередным числом.

Например: и т.д. Недостатком этого метода является наличие корреляции между числами последовательности, а в ряде случаев случайность вообще может отсутствовать.

Метод срединных квадратов вовсе не является случайным, то есть непредсказуемым (это наиболее существенный его недостаток). На самом деле, если мы знаем одно число, следующее число является полностью предопределенным, по­скольку правило его получения неизменно. Фактически, когда задается x0, предопределяется вся последовательность чисел xi. Это замечание касается всех арифметических генераторов.

Линейные конгруэнтные генераторы Широкое применение при моделировании на ЭВМ получили линейные конгруэнтные процедуры генерации псевдослучайных последовательностей. В них последовательность целых чисел определяется по рекурсивной формуле (6) где m (модуль), (множитель), c (приращение) и x0 (начальное число или значение) являются неотрицательными целыми числами. Таким образом, согласно формуле (6), для получения xi - нужно разделить на m, то есть xi будет остатком этого деления.

Два целых числа и конгруэнтны (сравнимы) по модулю m (m - целое число), если делится на m без остатка и если числа и дают одинаковые остатки от деления на m. Например: 125 и 5 (mod 10) m=10 Конгруэнтная процедура получения последовательностей случайных квазиравномерно распределенных чисел может быть реализована мультипликативным (с параметром c = 0) либо смешанным методом (с параметром c > 0).

Мультипликативный метод Задает последовательность неотрицательных целых чисел , не превосходящих m по формуле: (7) Для машинной реализации , где p=2, а q - число бит в машинном слове.

Алгоритм построения последовательности сводится к следующим шагам: выбрать в качестве x0 произвольное нечетное число; 2) вычислить коэффициент , где t - любое целое положительное число; 3) найти произведение , содержащие не более 2q значащих разрядов;

4) взять q младших разрядов в качестве первого члена последовательности Xi; 5) определить дробь - это и есть искомое число; 6) присвоить ; 7) вернуться к 3 пункту.

Cмешанный метод Сначала выбирается значение m. Чтобы получить длинный период и высокую плотность величин xi в интервале [0, 1], величина m должна иметь большое значение. Самым удачным выбором является m=2b, где b - число битов в слове задействованного компьютера.

Проверка качества последовательностей псевдослучайных чисел При моделировании важными характеристиками качества генератора являются длина периода p и длина отрезка апериодичности L. Длина отрезка апериодичност L псевдослучайной последовательности - есть наибольшее целое число, такое, что все числа xi в пределах этого отрезка не повторяются.

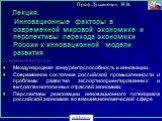
Способ экспериментального определения длины периода p и длины отрезка апериодичности L сводится к следующему: Запускается программа генерации последовательности {xi} с начальным значением x0 и генерируется V чисел xi. В большинстве случаев V - (1-5)106. Генерируются числа и фиксируется число xV. 2. Затем программа запускается повторно с начальным числом x0 и при генерации очередного числа проверяется истинность события p{xi=xV}. Если это событие истинно i=i1 и i=i2, то вычисляется длина периода последовательности p=i3-i1 . 3. Проводится запуск программы генерации с начальными числами x0 и xp. При этом фиксируется минимальный номер i=i3, при котором истинно событие p’’{xi=xp+i} и вычисляется длина отрезка апериодичности L=i3+p.

Рисунок 17 Представление определения длин периода p и отрезка периодичности L

Применяемые в имитационном моделировании генераторы случайных чисел должны пройти тесты на пригодность. Основные анализируемые характеристики генерируемых датчиком последовательностей: равномерность; стохастичность (случайность); независимость.

Существуют тесты двух типов. Эмпирические тесты — это обычный тип статистических тестов, они основаны на действительных значениях xi выдаваемых генератором. Теоретические тесты не являются тестами в том смысле, в каком они предусматриваются в статистике. Однако в них используются числовые параметры, чтобы оценить генератор глобально без фактического генерирования некоторых или всех значений xi.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

Метод Монте-Карло. Моделирование случайных величин. Моделирование непрерывных случайных величин. Способы формирования базовой случайной величины. Способы получения случайных чисел. Линейные конгруэнтные генераторы. Проверка качества последовательностей псевдослучайных чисел. Эмпирические тесты. Теоретические тесты.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Гультяев А.К. Имитационное моделирование в среде Windos. – СПб.: КОРОНА принт, 2001. – 400 с. Кийкова Е.В., Лаврушина Е.Г. Имитационное моделирование экономических процессов. Учебное пособие.- Владивосток: ВГУЭС, 2007. -128 с. Советов Б.Я., Яковлев С.А. Моделирование систем. Учебник для ВУЗов. - М.: Высшая школа, 2001.-344 с.

Использование материалов презентации Использование данной презентации, может осуществляться только при условии соблюдения требований законов РФ об авторском праве и интеллектуальной собственности, а также с учетом требований настоящего Заявления. Презентация является собственностью авторов. Разрешается распечатывать копию любой части презентации для личного некоммерческого использования, однако не допускается распечатывать какую-либо часть презентации с любой иной целью или по каким-либо причинам вносить изменения в любую часть презентации. Использование любой части презентации в другом произведении, как в печатной, электронной, так и иной форме, а также использование любой части презентации в другой презентации посредством ссылки или иным образом допускается только после получения письменного согласия авторов.