Конспект урока «ТЕОРЕМА ВИЕТА» по математике для 8 класса

Тема: ТЕОРЕМА ВИЕТА

Тип урока: изучение нового материала.

Класс: 8.

Цель урока: а) Знакомство с теоремой Виета и следствием.

б) Применение теоремы Виета в различных ситуациях.

в) развивать логическое мышление через мыслительные операции умение делать выводы, анализировать, применять знания в нестандартных ситуациях.

Материалы и оборудование урока: компьютор, презентация.

Ход урока (урок сопровождается презентацией):

I. Постановка цели урока.

На прошлых уроках вы познакомились с новыми уравнениями.

• Назовите их и дайте определение.

• В зависимости от наличия коэффициентов, на какие группы делятся квадратные уравнения?

• В зависимости от значения коэффициента а на какие группы делятся квадратные уравнения?

• Дайте определение приведенного квадратного уравнения.

Также познакомились с формулами корней квадратного уравнения и дискриминантом.

• Какую связь устанавливают формулы корней квадратного уравнения?

• Какую зависимость устанавливает значение дискриминанта?

А как вы думаете: все ли связи между корнями и коэффициентами квадратного уравнения мы рассмотрели?

Откройте тетради, запишите число и тему урока.

II. Проверка домашнего задания и формулирование проблемы.

№1

Исследование связи между корнями

и коэффициентами квадратного уравнения.

Обратимся к домашней работе. Дома вы решали 4 уравнения и заполняли таблицу.

№2.

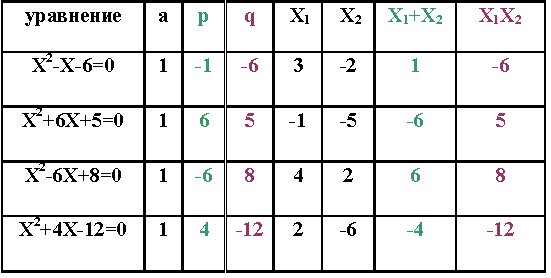
Проверьте свою работу по таблице. А теперь посмотрите внимательно, что интересного вы заметили? Обсудите это в парах и попытайтесь сформулировать предположение (выслушиваем предположения). Действительно, вы правы, существует такое утверждение.

III. Изучение нового материала.

№3.

Утверждение №1:

Пусть х₁и х₂ – корни уравнения х²+pх+q=0.

Тогда числа х₁, х₂ , p, q связаны равенствами:

х₁+х₂= -p, х₁х₂=q

Утверждение № 2:

Пусть числа х₁,х₂,p,q связаны равенствами х₁+х₂= -p, х₁х₂=q.

Тогда х₁и х₂ – корни уравнения х²+pх+q=0

Записываем в тетрадях и доказываем данные утверждения. (в процессе доказательства обратного утверждения получается равенство: х²+рх+q=(х-х₁)(х-х₂)).

Итак, мы доказали теорему Виета. Запишите ее в тетрадях.

№4

Теорема Виета:

Числа х₁ и х₂ являются корнями приведенного квадратного уравнения х²+pх+q=0 тогда и только тогда, когда х₁+х₂= -p, х₁х₂=q.

Следствие: х²+pх+q=(х-х₁)(х-х₂).

Как вы догадались, что данная теорема носит имя автора. Кем же был Франсуа Виет, и когда была доказана эта теорема?

№5

Франсуа Виет

Франсуа Виет родился в 1540 году во Франции. Отец Виета был прокурором. Сын выбрал профессию отца и стал юристом, окончив университет в Пуату. В 1563 году он оставляет юриспруденцию и становится учителем в знатной семье. Именно преподавание побудило в молодом юристе интерес к математике.

Виет переезжает в Париж, где легче узнать о достижениях ведущих математиков Европы. С 1571 года Виет занимает важные государственные посты, но в 1584 году он был отстранен и выслан из Парижа. Теперь он имел возможность всерьез заняться математикой.

В 1591 году он издает трактат «Введение в аналитическое искусство», где показал, что, оперируя с символами, можно получить результат, применимый к любым соответствующим величинам. Знаменитая теорема была обнародована в том же году.

Громкую славу получил при Генрихе lll во время Франко-Испанской войны. В течение двух недель, просидев за работой дни и ночи, он нашел ключ к Испанскому шифру.

Умер в Париже в 1603 году, есть подозрения, что он был убит.

Итак, какие связи между коэффициентами и корнями приведенного квадратного уравнения мы обнаружили? Чем интересно полученное следствие? Где это можно использовать?

Подумайте и ответьте: где, в каких ситуациях можно воспользоваться теоремой и следствием?

Свои предположения обсудите в парах и полученные ситуации запишите в тетрадь.

(выслушиваем то, что получилось, обсуждаем)

Давайте сравним ваши предположения с предлагаемыми ситуациями.

№6Ситуации, в которых может использоваться теорема Виета.

• Проверка правильности найденных корней.

• Определение знаков корней квадратного уравнения.

• Устное нахождение целых корней приведенного квадратного уравнения.

• Составление квадратных уравнений с заданными корнями.

• Разложение квадратного трехчлена на множители.

IV. Самостоятельная работа учащихся.

Выполним задания.

№7

Решите следующие задания:

1. Верно ли, что числа 15 и 7 являются корнями уравнения х² -22х+105=0?

2. Определите знаки корней уравнения х²+5х-36=0.

3. Найдите устно корни уравнения х² -9х+20=0.

4. Составьте квадратное уравнение, корнями которого являются числа 1/3 и 0,3.

5. Разложите квадратный трехчлен на множители х²+2х-48.

V. Постановка новой проблемы

Используя ответ задания №4, сначала переходим к квадратному уравнению с целыми коэффициентами, а затем задается вопрос: будет ли верна теорема Виета для данного неприведенного квадратного уравнения?

Учащиеся в парах обсуждают возникшую проблему, пробуют сформулировать по аналогии обобщенную теорему Виета. Обсуждаем полученные варианты ответов. Затем выясняем, как бы выглядело следствие для таких уравнений. Сравниваем со следующим слайдом.

№8

Обобщенная теорема Виета:

Числа х₁ и х₂ являются корнями квадратного уравнения ах²+bх+с=0 тогда и только тогда, когда х₁+х₂= -b/а, х₁х₂=с/а.

Следствие: ах²+bх+c=а(х-х₁)(х-х₂).

VI. Применение полученных знаний.

Учащимся предлагается применить полученные знания в следующих ситуациях.

№9

Решите следующие задания:

1. В уравнении х²+pх-32=0 один из корней равен 7. Найдите другой корень и коэффициент p.

2. Один из корней уравнения 10х² -33х+с=0 равен 5,3. Найдите другой корень и коэффициент с.

3. Разность корней квадратного уравнения х² -12х+q=0 равна 2. Найдите q.

4. Определите знаки корней квадратного уравнения ( если они существуют), не решая уравнения: 5х²-х- 108=0.

5. Найдите b и решите уравнение (b-1)· х²- (b+1)х = 72, если х₁ = 3.

Учащиеся решают в парах, полученные решения объясняют у доски. После решения этих заданий подводится итог урока.

VII. Итог урока. Задание на дом.

№10

Итог урока:

• Знакомство с теоремой Виета и следствием.

• Применение теоремы Виета в различных ситуациях.

Домашнее задание

№11

Домашнее задание:

Корни уравнения являются натуральными числами. Доказать, что - составное число.

п.24.прочитать, выучить теоремы и следствия.

№582(а, б, в), №584(а), №596(д)