Конспект урока «Применение производной в заданиях ЕГЭ» по математике для 11 класса

Муниципальное бюджетное общеобразовательное учреждение

« Средняя общеобразовательная школа № 52 г. Брянска»

Урок математики

в 11а классе.

Тема:

Применение производной в заданиях ЕГЭ

Учитель Руденок Е. В.

12.02.2014 г.

Тема : Применение производной в заданиях ЕГЭ.

Цель: 1.Обобщить и систематизировать знания учащихся по теме

«Применение производной».

2. Формировать умения в решении заданий на установление

связи свойств функции и свойств её производной с помощью

построения их графиков в одной системе координат.

3. Формировать умения в решении заданий на геометрический смысл

производной.

4. Развитие самостоятельной деятельности учащихся в проблемной

ситуации.

Девиз урока: «Слушаю – забываю.

Смотрю – запоминаю.

Делаю - понимаю»

Конфуций.

Оборудование: компьютер, два монитора (один монитор для демонстрации учащимся класса)

План урока.

1.Начало урока. Организационный момент.

Напоминание материала, изучаемого на последних уроках:

первообразная, вычисление первообразных.

Что такое первообразная функции? Как называется процесс отыскания функции по заданной производной?

Что такое дифференцирование?

Три понятия ФУНКЦИЯ, ПОИЗВОДНАЯ, ПЕРВООБРАЗНАЯ связаны друг с другом.

Вот в этой взаимосвязи мы сегодня и будем разбираться.

ФУНКЦИЯ y = f(x) производит на свет новую функцию y^’ = f ^‘(x).

ФУНКЦИЯ y = f(x) выступает в качестве «родителя», т. е. эта функция по отношению к функции y^’ = f ^‘(x) первичный образ или ПЕРВООБРАЗНАЯ.

Определение. Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке X, если для x принадлежащего Х выполняется равенство F’(x) = f(x).

С понятием первообразной мы знакомимся в 11 классе. Производную изучали в 10 классе.

Производная – одно из фундаментальных понятий математики. Для решения задач на применение производной требуется хорошее знание теоретического материала, умение проводить исследование различных ситуаций. При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов.  Её решение приводит к понятию производной. Сегодня мы будем говорить о применении производной в решении математических задач на ЕГЭ по математике.

В каких заданиях части В на ЕГЭ применяется производная?.

Какие основные элементы содержания задания В 9?

1. График функции.

2. График производной.

3. Геометрический смысл производной.

4. Физический смысл производной.

5. Первообразная функции.

Рассмотрим таблицу, на которой показана связь свойств функции и знака её производной. Таблица подготовлена заранее на боковой доске.

2. Презентация.

Посмотрим небольшую презентацию по теме урока, которая поможет вам вспомнить теорию, необходимую для решения задач. (См. приложение 1)

3. Решение задач № 1 - № 6 с использованием программы Winplotru.

Задача № 1.

Назвать промежутки возрастания функции. Какой знак имеет производная при x

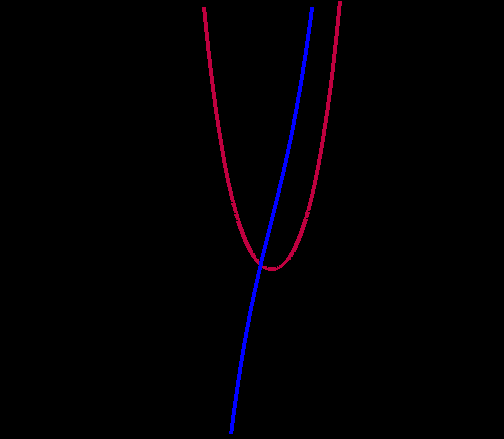
1. На рисунке изображены графики двух функций. Ученикам предлагается отметить, где изображён график функции, а где график её производной.

2. По выбору ученика для решения задачи оставляется на экране монитора один график.

3. На координатной прямой отметить стационарные точки, знаки производной и характер монотонности функции.

Ответ: Функция возрастает при неотрицательных значениях Х.

При хf ^‘(x)

Задача №2.

1. Назвать стационарные точки.

2. Назвать точку максимума функции.

3. Как зависит монотонность функции от знака производной ?

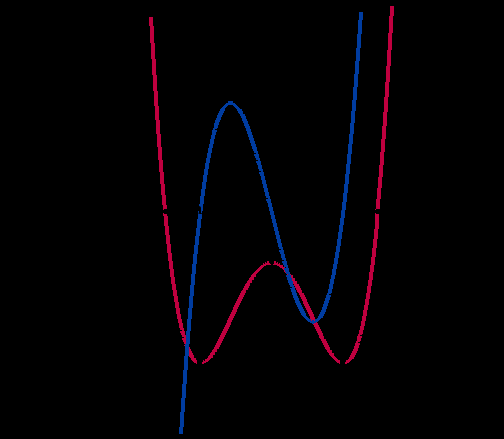
1. На рисунке изображены графики двух функций. Ученикам предлагается отметить, где изображён график функции, а где график её производной.

2. По выбору ученика на экране монитора оставлен график производной.

3. На координатной прямой отметить стационарные точки, знаки производной и характер монотонности функции.

Ответ: 1. а, 0, в

2. x_max = 0

3. При f ^‘(x)f ^‘(x)>0 функция возрастает.

Задача № 3.

Чем является график функция y = f (x) для графика функции

у = f ^’(x) ?

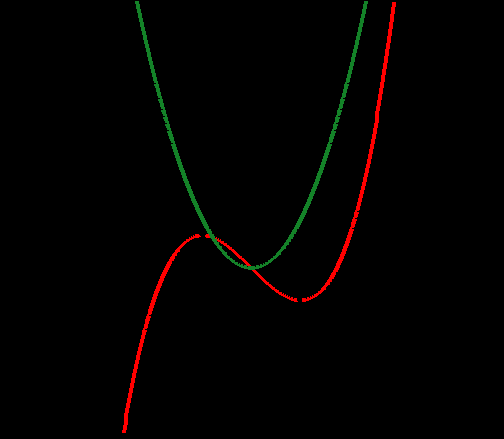
1. На рисунке изображены графики двух функций. Отметьте, где изображён график функции, а где график её производной.

2. График функции у = f (x) для графика функции у = f ^’(x) является графиком одной из первообразных.

3. Какой формулой задаётся множество всех первообразных ?

(y = 1/3 x³ – x + C)

4. Чему равно С в нашем случае? (С = -1)

5. На координатной прямой отметить стационарные точки, знаки производной и монотонность функции.

6. Изменится ли монотонность функции с изменением С? Почему?

Показать в программе Winplotru движение графика y = f (x) с изменением С.

Задача № 4.

Прямая y = kx + m является касательной к графику функции

y = ¼ x⁴ - 2 x ² – 2. Найти k и m.

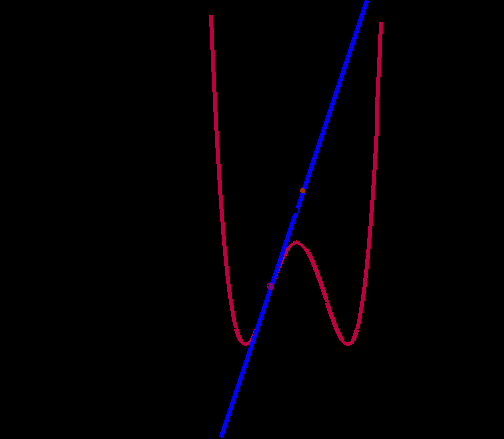
1. Что надо знать, чтобы ответить на вопрос этой задачи?

Геометрический смысл производной. (Как один из способов решения)

f ^’(x₀) = tg α = k = 0,75 / 0,25 = 3.

2. Как найти m ?

m = - 0,75

Ответ: k = 3, m = - 0,75.

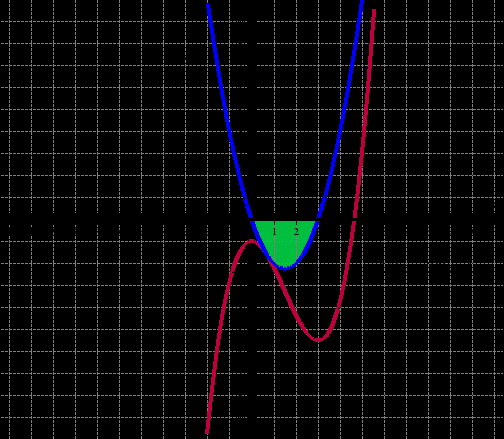
Задача № 5.

1. Найти угловой коэффициент касательной, проведённой к графику функции в точке, абсцисса которой равна: а) -1; б) 3.

2. Определить характер монотонности функции при 0x

1. а) Отметить точку на графике производной (-1;4), т.к. k = f ^’(-1) = 4.

б) Отметить точку на графике производной (3;0), т.к. k = f ^’(3) = 0.

Показать касательные в программе Winplotru.

2. При 0x

Ответ: 1. а) 4; б) 0.

2. при 0x

Задача № 6. (для самостоятельной работы)

Прямая y = 3 x- 4 является касательной к графику функции

y = 3 x² -3x + C.

Найти С.

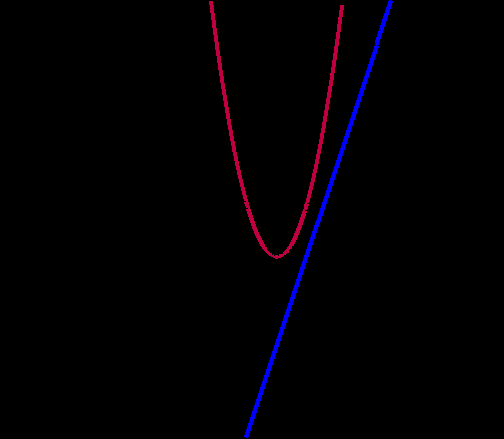
Что известно для того, чтобы начать решение задачи?

Коэффициент k = 3, f ^’(x₀) = tg α = k.

f ^’(x) =6х-3,

уравнение

6 x₀ - 3 = 3, x₀ =1 – абсцисса точки касания,

составим уравнение относительно С

3*1 – 4 = 3*1² – 3*1 + С,

откуда С =–1.

После решения учащимися задания проверяем, показывая касание в

программе Winplotru.

Ответ: С = -1.

4. Решение заданий В9 ЕГЭ по математике. Самостоятельная работа учащихся с проверкой и комментарием (у закрытой доски 2 человека) Условие заготовлено заранее.

1. Задание B9 (№ 6867)

На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых производная функции положительна.

f ^’(x)>0 на промежутках возрастания функции. При х = -2; -1; 5; 6, т. е. 4 точки. Ответ: 4.

2. Задание B9 (№ 317845)

На рисунке изображён график  производной функции  и восемь точек на оси абсцисс: , , , , . В скольких из этих точек функция  убывает?

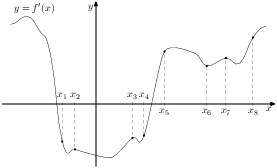
Функция убывает там, где производная отрицательна. Таких точек 4:

X₁^; X₂^; X₃^; X₄

Ответ: 4.

5. Итог урока.

Какие задания для вас сегодня показались наиболее сложными?

На что надо обращать внимание в первую очередь в заданиях В9?

По статистике правильно решают задание В9 около 64 % выпускников.

Надеюсь, что вы, продолжив подготовку по этому заданию, сможете решить его на ЕГЭ. Поэтому кроме домашнего задания вам предлагаются дополнительные задачи для самостоятельной подготовки.

Дополнительные задания для самоподготовки.

Задание B9 (№ 8305)

На рисунке изображен график  — производной функции , определенной на интервале . Найдите промежутки убывания функции . В ответе укажите длину наибольшего из них.

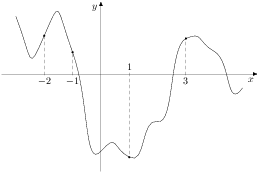
Задание B9 (№ 317945)

На рисунке изображен график функции  и отмечены точки -2, -1, 1, 3. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

Задания B9 (№ 323077)

На рисунке изображён график функции  — одной из первообразных некоторой функции , определённой на интервале . Пользуясь рисунком, определите количество решений уравнения  на отрезке .

Задание B9 (№ 9075)

На рисунке изображены график функции  и касательная к нему в точке с абсциссой . Найдите значение производной функции  в точке .

Домашнее задание.

Задание B9 (№ 317544) На рисунке изображен график функции 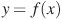 и отмечены точки -2, -1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

Задание B9 (№ 6869) На рисунке изображен график функции 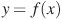, определенной на интервале 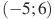. Определите количество целых точек, в которых производная функции положительна.

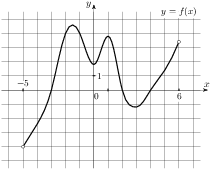
Задание B9 (№ 8551) На рисунке изображен график 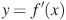 — производной функции 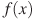, определенной на интервале . Найдите количество точек, в которых касательная к графику функции 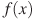 параллельна прямой  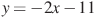или совпадает с ней.

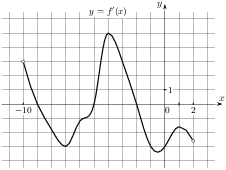
Задание B9 (№ 9057) На рисунке изображены график функции  и касательная к нему в точке с абсциссой . Найдите значение производной функции  в точке .

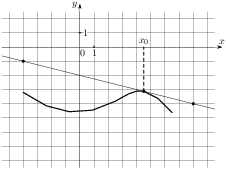
Задание B9 (№ 323081) На рисунке изображён график функции 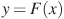 — одной из первообразных некоторой функции 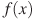, определённой на интервале 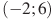. Пользуясь рисунком, определите количество решений уравнения  на отрезке .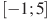

Список и источники литературы

1. Мордкович А.Г. «Алгебра и начала анализа» Ч.1. Учебник. Базовый уровень. Изд. Мнемозина

2. Мордкович А.Г. «Алгебра и начала анализа» Ч.2. Задачник. Базовый уровень. Изд. Мнемозина

3. http://alexlarin.net/

4. http://maerenkovavv.ru/

5. http://www.mioo.ru/ogl.php

6. www.mathege.ru