Конспект урока «Метод интервалов» по математике для 9 класса
Урок по теме "Метод интервалов ", 9-й класс
Цели:
Деятельностная цель: формирование умений применением метода интервалов при решении простейших неравенств с кратными корнями.
Содержательная цель: расширение знаний учащихся по теме «Решение неравенств с одной переменной»
Тип урока: урок «открытия» нового знания
Ход урока:
1) организационный момент.
2) проверка домашнего задания (два человека на доске).
3) Актуализация знаний
Остальные учащиеся: повторяем алгоритм решения неравенств методом интервалов.
Решить неравенство (с проведением сравнительного анализа решения):
а)(x + 5)(x + 4)(x – 5)
б) (x – 5)(x + 4)(x + 5)2 ≤ 0.
(x – 5)(x + 4)(x + 5)2 ≤ 0 (x - 5)(x+4) ≤ 0, x = - 5;
Ответ. х € { - 5} U [- 4; 5]
Прежде всего, отметим, что если в разложении многочлена на множители входит сомножитель ![]() , то говорят, что
, то говорят, что ![]() - корень многочлена кратности
- корень многочлена кратности ![]() .
.
Значит, корень х = -5 кратности 2.
Вопросы: Что вы заметили при решении данных неравенств? (не чередуются знаки на интервалах в неравенстве б)
Эта ситуация осложняет решение неравенств? (да, теперь знаки функции необходимо проверять на каждом интервале!)
А может, есть способ, все- таки не менять привычный алгоритм решения? (возможно есть)
Сформулируйте тему нашего урока:
Метод интервалов при решении неравенств с кратными корнями
Какие цели?
Научиться применять метод интервалов при решении неравенств с кратными корнями.
4)Проблемное объяснение нового знания
Итак, причина затруднения применения метода интервалов: не чередуются знаки на интервалах, что приводит к необходимости проверки знаков функции на каждом интервале.
Решим неравенство: (x – 5)(x + 4)(x + 5)2 ≤ 0 другим способом:
(x – 5)(x + 4)(x + 5)(x + 5) ≤ 0
Введем функцию f(x) = (x – 5)(x + 4)(x + 5)2; Д(f)=R.
Найдем нули функции f(x) = (x – 5)(x + 4)(x + 5)2, решив уравнение (х-5)(х+4)(х+5)2 = 0.
x = 5; x = - 4; x = - 5 и x = - 5.
- 5 – корень кратности 2 (две слившиеся точки), между ними интервал с началом и концом в точке -5. Давайте введем интервал с началом и концом в точке -5. (его длина равна 0)
Нули функции разбивают область определения на интервалы, в каждом из которых функция непрерывна и сохраняет свой знак.
Определим знак функции f (x) = (x - 5)(x + 4)(x + 5)2 при
x = 0, f (0) = (0 - 5)(0 + 4)(0 + 5)2
= 0, f (0) = (0 - 5)(0 + 4)(0 + 5)2

х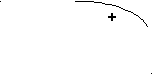


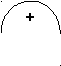
-5 -4 5
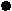
Чередуя, расставим знаки в каждом интервале, учитывая «лепесток», т.е. интервал с началом и концом в точке-5, и по рисунку запишем решение исходного неравенства.
Ответ: {-5} U [-4; 5]
Надо менять алгоритм решения неравенств методом интервалов? Определять знаки функции на каждом интервале? Как поступать с кратными корнями?
5) Закрепление
а) Работа в парах. Заполнить пропуски в карточке
При решении неравенств с кратными корнями необходимо:
1. Найти ______________ функции f(х) = (х – х1)(х – х2) … (х – хп)
2. Изобразить на ____________________________________ функции.
3. В точках, которые являются кратными корнями, дорисовать нулевые интервалы в виде ______________________.
4. Количество лепестков равно _____________.
5. Определить ____________ функции на одном из интервалов и _________________ знаки на остальных интервалах, включая ________________.
6. При этом знаки____________________ на всех интервалах.
7. Записать _________________, в соответствии с условием.
Заполнение проверить по слайду. Определить количество ошибок, расставляя знаки «+» или «- »
Проговорить алгоритм в парах с учетом допущенных ошибок.
б) Решение неравенств.
На доске два ученика решают неравенства. Остальные работают в тетрадях.
Примеры:
№1. Решить неравенство: (x – 1)(3 – x)4 (x – 2) ≤ 0.
Введем функцию f(x) = (x - 1)(3 –x)4 (x – 2), Д (f) = R.
Нули функции: x =1; x =2; x =3 – корень кратности 4.
Сколько «лепестков» рисуем в точке х=3?
В точке х = 3 дорисуем 3 «лепестка».
точке х = 3 дорисуем 3 «лепестка».
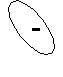
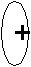

х
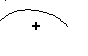


2 1 3
Определим знак функции f(x) на любом промежутке, например (-∞; 1)
f(0) = (0 -1)(3 – 0) (0 -2) > 0,
и, чередуя, проставим знаки.
Ответ: [1; 2] U{3}
№2. Решить неравенство: x2(x + 2)(x – 1)3 ≥ 0.
f(x) = x2(x + 2)(x – 1)3, Д(f)=R.
Нули функции: x = 0 - кратность 2,
x = -2,
x = 1 - кратность 3.

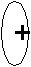
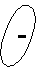


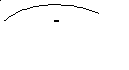

х
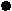
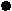
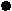
1 0 -2
Определим знаки функции f (x) на любом промежутке, например (-∞; -2).
f (-1) =
f (x) ≥ 0: (- ∞; 2] U {0} U [1; +∞).
Ответ: (-∞; 2] U {0} U [1; +∞).
Физкультминутка.
6) Самостоятельная работа (с взаимопроверкой в парах).
Запишите три любых числа a, b, с, причем a
(x – a)(x – b)2(x – c) ≥ 0.
7)Итоги самостоятельной работы
8)Итоги урока.
Каждый получает карточку с алгоритмом. Ее вклеить в тетрадь.
Алгоритм решения неравенств с кратными корнями
(х – х1)(х – х2)к … (х – хп)≥0
1. Найти нули функции f(х) = (х – х1)(х – х2)к … (х – хп)
2. Изобразить на координатной прямой нули функции.
3. В точках, которые являются кратными корнями, дорисовать нулевые интервалы в виде лепестков.
4. Количество лепестков равно k – 1 ( где к – это кратность корня).
5. Определить знаки функции на одном из интервалов и расставить знаки на остальных интервалах, включая «лепестки», чередуя знаки.
6. Записать ответ, в соответствии с условием.
8)Домашнее задание:
1) №390 (в, г)
2) Попытаться решить неравенство (x – 5)2(2 + x)(x + 3)3/ (x + 4)(x – 4) ≤ 0.
Здесь представлен конспект к уроку на тему «Метод интервалов», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

